„A kényszerrezgés vizsgálata” változatai közötti eltérés

A Fizipedia wikiből
 
(2 szerkesztő 35 közbeeső változata nincs mutatva)
12. sor: 12. sor:
 
<!--[[Kategória:Informatika]]-->  
 
<!--[[Kategória:Informatika]]-->  
 
[[Kategória:Laborgyakorlat]]
 
[[Kategória:Laborgyakorlat]]
−
<!--[[Kategória:Fizika laboratórium 1.]]-->
+
[[Kategória:Fizika laboratórium 1.]]
−
[[Kategória:Fizika laboratórium 2.]]
+
<!--[[Kategória:Fizika laboratórium 2.]]-->
 
<!--[[Kategória:Fizika laboratórium 3.]]-->
 
<!--[[Kategória:Fizika laboratórium 3.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
 
<!--[[Kategória:Fizika laboratórium 4.]]-->
19. sor: 19. sor:
  
 
A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul.
 
A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul.
 +
 +
Ebben a mérésben mechanikai rezgéseket fog tanulmányozni. Az ezzel teljesen analóg módon leírható elektromos rezgőköröket az [[RLC körök mérése|RLC körök mérésében]] tanulmányozza. A két mérésből közös jegyzőkönyvet kell készítenie.
  
  
27. sor: 29. sor:
 
===Csillapítatlan rezgések===
 
===Csillapítatlan rezgések===
  
−
Ha egy $m$ tömegű anyagi pontra rugalmas erő hat, akkor a mozgásegyenlet $ma=-sx$ alakú, ahol $s$ a rugóállandó, $x$ a tömegpont kitérése az egyensúlyi helyzetből, $m$ a tömeg, és $a$ a gyorsulás.  
+
Ha egy $m$ tömegű anyagi pontra a kitéréssel arányos, rugalmas erő hat, akkor a mozgásegyenlet
 +
$$ma=-Dx$$
 +
alakú, ahol $D$ a rugóállandó, $x$ a tömegpont kitérése az egyensúlyi helyzetből, $m$ a tömeg, és $a$ a gyorsulás.  
 
A mozgásegyenlet megoldása
 
A mozgásegyenlet megoldása
−
{{eq|x{{=}}A\sin(\omega_0 t+\alpha),|eq:1|(1)}}
+
$$x(t)=A\sin(\omega_0 t+\alpha)$$
−
ahol $A$ a kitérési amplitúdó, $\alpha$ a $t=0$ időpillanathoz tartozó fázis,
+
ahol $A$ a (kitérési) amplitúdó, $\alpha$ a $t=0$ időpillanathoz tartozó fázis (mindkettőt a kezdeti feltételek határozzák meg),
−
{{eq|\omega_0{{=}}\sqrt{\frac{s}{m} }|eq:2|(2)}}
+
$$\omega_0=\sqrt{\frac{D}{m}}$$
−
a csillapítatlan rezgő rendszer körfrekvenciája ($\omega_0=2\pi f_0$, ahol $f_0$ a megfelelő frekvencia). A harmonikus rezgőmozgás sebessége  
+
a csillapítatlan rezgő rendszer körfrekvenciája. ($\omega_0=2\pi f_0$, ahol $f_0$ a megfelelő frekvencia.)
−
$$v=\frac{\text{d} x}{\text{d} t}=A\omega_0\cos(\omega_0 t+\alpha),$$
+
 
−
ahol $A\omega_0$ a maximális sebesség, a sebesség-amplitúdó.
+
A harmonikus rezgőmozgás sebessége
 +
$$v(t)=\frac{\text{d} x}{\text{d} t}=A\omega_0\cos(\omega_0 t+\alpha)$$
 +
ahol $A\omega_0$ a maximális sebesség, az ún. sebességamplitúdó.
  
 
===Csillapodó rezgések===
 
===Csillapodó rezgések===
  
−
A csillapodást okozó erők gyakran a sebességgel arányosak. Ekkor a tömegpont mozgásegyenlete: $ma=-sx-k\nu$, ami a $\delta=\frac{k}{2m}$ csillapodási tényező ($k$ a súrlódásra jellemző mennyiség) és [[#eq:2|(2)]] felhasználásával az alábbi alakra hozható:
+
A csillapodást okozó erők gyakran (jó közelítéssel) a sebességgel arányosak: $F_{cs}=-kv$, ahol $k$ a csillapítás erősségére jellemző mennyiség. Ekkor a tömegpont mozgásegyenlete:
−
$$\frac{\text{d}^2x}{\text{d}t^2}+2\delta\frac{\text{d}x}{\text{d}t}+\omega^2 x=0.$$
+
$$ma=-Dx-kv$$
−
A differenciálegyenlet megoldása $\omega_0^2\geq\delta^2$ esetén időben csökkenő amplitúdójú lengéseket eredményez:  
+
ami a $\beta=k/(2m)$ csillapítási tényező bevezetésével és $\omega_0$ definíciójának felhasználásával az alábbi alakra hozható:
−
$$x=A\exp(-\delta t)\sin(\omega' t+\alpha).$$
+
$$\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=0$$
 +
A differenciálegyenlet megoldása $\omega_0^2\geq\beta^2$ esetén időben csökkenő amplitúdójú lengéseket eredményez:  
 +
$$x(t)=Ae^{-\beta t}\sin(\omega' t+\alpha)$$
 
A rezgés körfrekvenciája
 
A rezgés körfrekvenciája
−
$$\omega'=\sqrt{\omega_0^2-\delta^2}.$$
+
$$\omega'=\sqrt{\omega_0^2-\beta^2}$$
−
Az amplitúdó változás jellemzésére különböző mennyiségeket használnak. A csillapodási hányados két, azonos irányban egymás után kővetkező amplitúdó hányadosa $K=\frac{x_n}{x_{n+1} }=\exp(\delta T)$ , ahol $T=\frac{2\pi}{\omega}$. Használatos még a K csillapodási hányados logaritmusa, az ún. logaritmikus dekrementum:
+
Az amplitúdóváltozás jellemzésére különböző mennyiségeket használnak. A csillapodási hányados két, azonos irányban egymás után következő amplitúdó hányadosa
−
{{eq|\Lambda{{=}}\ln K{{=}}\delta T.|eq:3|(3)}}
+
$$K=\frac{x_n}{x_{n+1} }=e^{\beta T}$$
 +
ahol $T=2\pi/\omega'$. Használatos még a K csillapodási hányados logaritmusa, az ún. logaritmikus dekrementum is:
 +
$$\Lambda=\ln K=\beta T$$
  
 
===Kényszerrezgések===
 
===Kényszerrezgések===
  
−
Egy m tömegre motor és excenter segítségével időben periodikusan változó erőt alkalmazva egy átmeneti időszak után időben állandósult rezgés alakul ki, melynek frekvenciája megegyezik a kényszerítő erő frekvenciájával, míg amplitúdója függ az erőtől, a rugóállandótól, a tömegtől, a csillapítástól valamint a gerjesztő frekvenciától. Az anyagi pont mozgásegyenlete ekkor: . Az [[#eq:1|(1)]] egyenletnél bevezetett jelöléseket alkalmazva másodrendű lineáris, inhomogén differenciálegyenletet kapunk:
+
Egy $m$ tömegre pl. motor és excenter segítségével időben periodikusan változó erőt alkalmazva egy átmeneti időszak után időben állandósult rezgés alakul ki, melynek frekvenciája megegyezik a kényszerítő erő frekvenciájával, míg amplitúdója függ az erőtől, a rugóállandótól, a tömegtől, a csillapítástól valamint a gerjesztő frekvenciától. Az anyagi pont mozgásegyenlete ekkor:
−
$$\frac{\text{d}^2x}{\text{d}t^2}+2\delta\frac{\text{d}x}{\text{d}t}+\omega^2 x=\frac{F_0}{m}\sim(\omega t),$$
+
$$ma=-Dx-kv+F_0\sin(\omega t)$$
 +
A korábban bevezetett jelöléseket alkalmazva másodrendű lineáris, inhomogén differenciálegyenletet kapunk:
 +
$$\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=\frac{F_0}{m}\sin(\omega t)$$
 
ahol $F_0$ a kényszererő maximális értéke. Az egyenlet megoldása:
 
ahol $F_0$ a kényszererő maximális értéke. Az egyenlet megoldása:
−
{{eq|x{{=}}A\exp(-\delta t)\sin(\omega' t+\alpha)+\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2\omega^2} }\sin(\omega t+\varphi)|eq:4|(4)}}
+
$$x(t)=A_0e^{-\beta t}\sin(\omega' t+\alpha)+\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} }\sin(\omega t+\varphi),$$
−
melynek második tagja írja le az állandósult állapotot. A $\varphi$ fázisállandó nem az időmérés kezdetétől függ, hanem a kényszerítő erő fázisától való eltérés. Az állandósult állapot amplitúdójának maximuma van az
+
melynek második tagja írja le az állandósult állapotot. Az állandósult állapot amplitúdója:
−
{{eq|\omega_{\text{max} }{{=}}\sqrt{\omega_0^2-2\delta^2}|eq:5|(5)}}
+
$$A(\omega)=\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} },$$
−
frekvenciánál, míg a fázisállandó
+
melynek maximuma van az
−
$$\text{tg}\varphi=\frac{2\delta\omega}{\omega_0^2-\omega^2}.$$
+
$$\omega_{max}=\sqrt{\omega_0^2-2\beta^2}$$
 +
körfrekvenciánál. A $\varphi$ fázisállandó nem az időmérés kezdetétől függ, hanem a kényszerítő erő fázisától való eltérés, ennek tangense:
 +
$$\text{tg}\varphi=\frac{2\beta\omega}{\omega_0^2-\omega^2}.$$
 +
Az amplitúdóhoz hasonlóan megadhatjuk a sebességamplitúdó kifejezését is:
 +
$$A\omega=\frac{F_0\omega}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}}$$
 +
melynek maximuma – ellentétben a kitérési amplitúdó maximumával – éppen $\omega_0$-nál van, ahol
 +
$$A\omega_0=\frac{F_0}{2m\beta}.$$
 
A kényszerrezgés energiaviszonyainak jellemezésére az egy periódus alatt disszipált energia $\langle W\rangle$ és a rendszerben tárolt átlagos energia $\langle P\rangle$ hányadosával arányos ''jósági tényező''t használjuk
 
A kényszerrezgés energiaviszonyainak jellemezésére az egy periódus alatt disszipált energia $\langle W\rangle$ és a rendszerben tárolt átlagos energia $\langle P\rangle$ hányadosával arányos ''jósági tényező''t használjuk
−
$$Q=2\pi\frac{\langle W\rangle}{T\langle P\rangle}=\frac{\omega_0}{2\delta}.$$
+
$$Q=2\pi\frac{\langle W\rangle}{T\langle P\rangle}\approx\frac{\omega_0}{2\beta}$$
  
 
==A kísérleti berendezés leírása==
 
==A kísérleti berendezés leírása==
−
{{fig|A_kényszerrezgés_vizsgálata_1.png|fig:1|1. ábra}}
 
  
−
A kísérleti berendezés az [[#fig:1|1. ábrán]] látható. Az alul elhelyezkedő elektronikai egység hátsó lapján található a kényszererőt létrehozó excenter. A kényszererő amplitúdója az amplitúdó-rúd helyzetének változtatásával szabályozható, ami a kényszert kifejtő zsinór rögzítési pontja és az excenter középpontja közötti távolságot befolyásolja [[#fig:2|(2. ábra)]]. A kényszert továbbító zsinór a tartóoszlop tetején található két csiga vájatain áthaladva egy hurokkal kapcsolódik a vizsgálandó rugó egyik végéhez. A másik véghez a skálával ellátott mérőrúd és a hozzá erősített ún. csillapító rúd csatlakozik. E két rúd alkotja a rezgőmozgást végző "alaptömeget", melynek értéke 50 g.
+
{{fig2|Kenyszerrezges.png|fig:1|1. ábra}}
  
−
{{fig|A_kényszerrezgés_vizsgálata_2.png|fig:2|2. ábra}}
+
A kísérleti berendezés az [[#fig:1|1. ábrán]] látható. Az alul elhelyezkedő elektronikai egység hátsó lapján található a kényszererőt létrehozó excenter. A kényszererő amplitúdója az amplitúdórúd helyzetének változtatásával szabályozható, ami a kényszert kifejtő zsinór rögzítési pontja és az excenter középpontja közötti távolságot befolyásolja [[#fig:2|(2. ábra)]]. A kényszert továbbító zsinór a tartóoszlop tetején található két csiga vájatain áthaladva egy hurokkal kapcsolódik a vizsgálandó rugó egyik végéhez. A másik véghez a skálával ellátott mérőrúd és a hozzá erősített ún. csillapító rúd csatlakozik. E két rúd alkotja a rezgőmozgást végző „alaptömeget”, melynek értéke 50 g.
  
−
A mérőkészlethez tartozik két 50 g tömegű rézkorong is. A korongokat a mérőrudat és csillapitórudat összekötő csavarmenetre lehet felerősíteni. A tartóoszlop középmagasságánál látható a rúdvezető, melyben optikai érzékelő van. A mérőrudat a rúdvezető téglalap alakú nyílásán kell átvezetni.
+
A mérőkészlethez tartozik két 50 g tömegű rézkorong is. A korongokat a mérőrudat és csillapitórudat összekötő csavarmenetre lehet felerősíteni. A tartóoszlop középmagasságánál látható a rúdvezető, melyben optikai érzékelők vannak. A mérőrudat a rúdvezető téglalap alakú nyílásán kell átvezetni.
  
−
Helyes beállítás után a rezgés csillapodása - melyet a légellenállás ill. a berendezés egyes elemei között fellépő súrlódás okoz - igen kicsi. Ezért a csillapítás változtatása (növelése) céljából a kővetkezőképpen járhatunk el.
+
Helyes beállítás esetén a rezgés csillapodása – melyet a légellenállás ill. a berendezés egyes elemei között fellépő súrlódás okoz – igen kicsi. Ezért a csillapítás változtatása (növelése) céljából a tartórúdra egy olyan mágnespárt szerelhetünk fel, melynek pofái között a távolság változtatható. Ezen mágnespofák között mozog az alumíniumból készült csillapítórúd. A mágneses tér hatására a mozgó fémrúdban örvényáramok keletkeznek, melyek Joule-hőjének disszipációja okozza a rendszer csillapodását. A mágnespofák közötti távolság csökkentésével a mágneses térerősség növelhető, azaz a disszipáció, vagyis a csillapítás fokozható.
−
 
+
−
A tartórúdra egy olyan mágnes-párt szerelünk fel, melynek pofái között a távolság változtatható. Ezen mágnespofák között mozog az alumíniumból készült csillapítórúd. A mágneses tér hatására a mozgó fémrúdban örvényáramok keletkeznek, melyek Joule-hőjének disszipációja okozza a rendszer csillapodását. A mágnespofák közötti távolság csökkentésével a mágneses térerősség növelhető, azaz a disszipáció, vagyis a csillapítás fokozható.
+
  
 
===Beállítás===
 
===Beállítás===
−
{{fig|A_kényszerrezgés_vizsgálata_3.png|fig:3|3. ábra}}
 
  
−
# Ha a készülék jól van beállítva, a mérőrúd úgy függ, hogy egyik oldala sem ér hozzá a rúdvezető nyílásának falához ([[#fig:3|3. ábra]]). A nem jó a beállítás a 3. ábrán látható "b" vagy "c" esetben fordul elő. A "b" esetet az elektronika doboz változtatható magasságú lábainak megfelelő állításával korrigálhatjuk (vízszintezés). A "c" eset a mérőrúd felfüggesztésével javítható.
+
*Ha a készülék jól van beállítva, a mérőrúd úgy függ, hogy egyik oldala sem ér hozzá a rúdvezető nyílásának falához ([[#fig:3|3. ábra]]). A nem jó a beállítás a 3. ábrán látható „b” vagy „c” esetben fordul elő. A „b” esetet az elektronika doboz változtatható magasságú lábainak megfelelő állításával korrigálhatjuk (vízszintezés). A „c” eset a mérőrúd felfüggesztésével (elcsavarásával)javítható.
−
# A fázis és amplitúdó pontos méréséhez úgy kell felfüggeszteni a mérőrudat, hogy egyensúlyi helyzetben  középvonala egybeessen a rúdvezető optikai érzékelőjével. Hogy ezt beállíthassa:
+
*A fázis és amplitúdó pontos méréséhez úgy kell felfüggeszteni a mérőrudat, hogy egyensúlyi helyzetben  középvonala egybeessen a rúdvezető optikai érzékelőjével. Ennek beállításához:
−
## Kapcsolja be az elektronika doboz hátoldalán levő kapcsolót. Figyelje a rúdvezető LED-et. Ha a mérőrúd középvonala (8,5 cm) feljebb van, mint a rúdvezető felső éle, akkor a LED kialszik. Ha a középvonal lejjebb került, akkor a LED kigyullad.
+
**Kapcsolja be az elektronika doboz hátoldalán levő kapcsolót. Figyelje a rúdvezető LED-et. Ha a mérőrúd középvonala (8,5 cm) feljebb van, mint a rúdvezető felső éle, akkor a LED kialszik. Ha a középvonal lejjebb került, akkor a LED kigyullad.
−
## Mozgassa úgy a mérőrudat, fel és le, hogy a középvonala áthaladjon a rúdvezetőn. Közben figyelje a FÁZIS kijelzést. Amikor a mérőrúd középvonala lefelé halad keresztül a rúdvezetőn, egy LED villog a fázisskálán. Annyira fordítsa el a kényszerkereket, hogy a fázist jelző LED éppen 0° fázishelyzetet mutasson.  
+
**Mozgassa úgy a mérőrudat fel és le, hogy a középvonala áthaladjon a rúdvezetőn. Közben figyelje a FÁZIS kijelzést. Amikor a mérőrúd középvonala lefelé halad keresztül a rúdvezetőn, egy LED villog a fázisskálán. Annyira fordítsa el a kényszerkereket, hogy a fázist jelző LED éppen 0° fázishelyzetet mutasson.  
−
## Most pontosítsa a zsinór hosszát. Ez a zsinóron található plasztikcsattal állítható. Finom állítások a tartóoszlop tetején levő csavarral végezhetők. A zsinórhossz akkor megfelelő, ha egészen kicsi oszcillációknál a fázis LED ki-be kapcsol.
+
**Most pontosítsa a zsinór hosszát. Ez a zsinóron található plasztikcsattal állítható. Finom állítások a tartóoszlop tetején levő csavarral végezhetők. A zsinórhossz akkor megfelelő, ha egészen kicsi oszcillációknál a fázis LED ki-be kapcsol.
  
−
{{fig|A_kényszerrezgés_vizsgálata_4.png|fig:4|4. ábra}}
+
Az elektronika doboz a [[#fig:4|4. ábrán]] látható. Az elülső lapon található a DRIVE kapcsoló. Ezzel indítható a motor, mely a kényszer kereket forgatja.
 +
A FREQUENCY gombbal változtatható a kényszer frekvenciája. Óramutató járásával megegyezően forgatva növeli a frekvenciát.
 +
A FUNCTION kapcsoló határozza meg azt, hogy az alábbi három változóból melyiket írja ki a digitális kijelző. (A kijelző jobb oldalán egy LED mutatja, hogy melyik változó értéket olvashatjuk le.)
 +
*FREQ. – A kényszerkerék frekvenciája (Hz)
 +
*AMPL. – A mérőrúd csúcstól-csúcsig amplitúdója (ez az amplitúdó kétszerese) (mm)
 +
*PERIOD – A mérőrúd egy teljes rezgésének periódusideje (s).
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|A_kényszerrezgés_vizsgálata_2.png|fig:2|2. ábra}}
 +
| {{fig|A_kényszerrezgés_vizsgálata_3.png|fig:3|3. ábra}}
 +
| {{fig|A_kényszerrezgés_vizsgálata_4.png|fig:4|4. ábra}}
 +
|-
 +
|}
  
−
Az elektronika doboz a [[#fig:4|4. ábrán]] látható. Az elülső lapon található a ''DRIVE'' kapcsoló. Ezzel indítható a motor, mely a kényszer kereket forgatja.
 
−
A ''FREKVENCIA'' gombbal változtatható a kényszer frekvenciája. Óramutató járásával megegyezően forgatva növeli a frekvenciát.
 
−
A ''FUNKCIÓ'' kapcsoló határozza meg azt, hogy az alábbi három változóból melyiket írja ki a digitális kijelző. A kijelző jobb oldalán egy ''LED'' mutatja, hogy melyik változó értéket olvashatjuk le.
 
−
* ''FREQ.'' - A kényszerkerék frekvenciája (Hz)
 
−
* ''AMPL.'' - A mérőrúd csúcstól-csúcsig amplitúdója (ez az amplitúdó kétszerese) (mm)
 
−
* ''PERIOD'' - A mérőrúd egy teljes rezgésének periódusideje (s).
 
  
 
==Mérési feladatok==
 
==Mérési feladatok==
 +
 +
[[A méréshez rendelkezésre álló eszközök: A kényszerrezgés vizsgálata|A méréshez rendelkezésre álló eszközök]]
  
 
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
 
*''A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.''
101. sor: 124. sor:
 
'''2.''' Csillapítatlan rendszer lengésideje
 
'''2.''' Csillapítatlan rendszer lengésideje
  
−
Szabályozza be a készüléket! (Beállítás A és B pontok alapján) Ehhez a méréshez szerelje le a csillapító mágnes-pofákat! ''FUNKCIÓ'' kapcsolót állítsa ''PERIÓDUS-MÉRÉSRE''. Húzza a mérőrudat kb. 5 cm-rel az egyensúlyi helyzete alá, aztán engedje el! A digitális kijelző ekkor a rezgés ''PERIÓDUSIDEJÉT'' (s) mutatja. A mérést üres mérőrúddal, majd 50 és 100 g-os terhelésekkel is végezze el! Az eredményeket foglalja táblázatba és vesse össze az elmélet alapján kiszámolt értékekkel!
+
Szabályozza be a készüléket!
 +
*''Nagyon fontos, hogy a mérőrúd ne érjen a rúdvezető egyik falához se (lásd az [[#Beállítás|előző pontban]])!''
 +
Ehhez a méréshez szerelje le a csillapító mágnespofákat! A funkciókapcsolót állítsa periódusidőmérésre (PERIOD). Húzza a mérőrudat kb. 5 cm-rel az egyensúlyi helyzete alá, és engedje el! A digitális kijelző ekkor a rezgés periódusidejét (s) mutatja. A mérést üres mérőrúddal, majd 50 és 100 g-os terhelésekkel is végezze el!
 +
*''Az eredményeket foglalja táblázatba és vesse össze az elmélet alapján kiszámolt értékekkel!''
  
−
'''3.''' Kényszerrezgés amplitúdójának és sebesség-amplitúdójának vizsgálata a kényszerítő frekvencia függvényében
+
'''3.''' Kényszerrezgés amplitúdójának és sebességamplitúdójának vizsgálata a kényszerítő frekvencia függvényében
  
−
A méréseket két különböző csillapítás esetén, mindkét esetben kétféle tömeggel (mérőrúd + 50 g, mérőrúd + 100 g) végezze el! Szerelje vissza a csillapító mágnespofákat! A kis csillapításhoz a csillapító mágnespofákat egymástól a lehető legtávolabb állítsa be! A nagy csillapításhoz tekerje a mágnespofákat a lehető legközelebb, de csak annyira, hogy ne érjenek hozzá a csillapítórúdhoz! Ekkor mérje meg és jegyezze fel a mágnespofák távolságát!
+
A méréseket két különböző csillapítás esetén, mérőrúd + 50 g tömeggel végezze el! Szerelje vissza a csillapító mágnespofákat! A kis csillapításhoz a csillapító mágnespofákat egymástól a lehető legtávolabb állítsa be! A nagy csillapításhoz tekerje a mágnespofákat a lehető legközelebb, de csak annyira, hogy ne érjenek hozzá a csillapítórúdhoz! Ekkor mérje meg és jegyezze fel a mágnespofák távolságát!
  
−
Gondosan állítsa be a mérőrúd helyzetét úgy, hogy már egészen kis kitéréseknél villogjon a digitális kijelző (beállítás 2/2 pont)! A FUNKCIÓ kapcsolót állítsa FREKVENCIA mérésre és a ''DRIVE'' kapcsolóval indítsa el a kényszerrezgést! A ''FREKVENCIA'' szabályozó gombbal lassan (fokozatosan) növelje a frekvenciát, és időről-időre váltson át az ''AMPLITÚDÓ'' funkcióra! (Itt a kijelző mm-ben megadja a csúcstól-csúcsig amplitúdót – ez az amplitúdó kétszerese.) Figyelje eközben a fázisállandót jelző ''LED'' értékét! Amikor a kényszerítő frekvencia megegyezik az $f_0$ sajátfrekvenciával, a fázisszög 90°. Keresse meg az $f_{\text{max} }$ rezonanciafrekvenciát, ahol az amplitúdó maximális! [A rezonanciafrekvencia – különösen nagy csillapítás esetében – eltér a sajátfrekvenciától [[#eq:5|(5)]].] Amennyiben a rezgések amplitúdója túl nagy vagy túl kicsi lenne, úgy kapcsolja ki a készüléket és csökkentse, illetve növelje a kényszererő amplitúdóját, majd ellenőrizze a kitérést a rezonanciafrekvenciánál!
+
Gondosan állítsa be a mérőrúd helyzetét úgy, hogy már egészen kis kitéréseknél villogjon a digitális kijelző ([[#Beállítás|beállítás]])! A funkciókapcsolót állítsa frekvenciamérésre (FREQ.) és a DRIVE kapcsolóval indítsa el a kényszerrezgést! A frekvenciaszabályozó gombbal lassan (fokozatosan) növelje a frekvenciát, és időről-időre váltson át az amplitúdómérésre (AMPL.)!
 +
*''Itt a kijelző mm-ben megadja a csúcstól-csúcsig amplitúdót – ez az amplitúdó kétszerese.''
 +
*''Figyelje eközben a fázisállandót jelző LED értékét is! Amikor a kényszerítő frekvencia megegyezik az $f_0$ sajátfrekvenciával, a fázisszög 90°.''
 +
Keresse meg az $f_{max}$ rezonanciafrekvenciát, ahol az amplitúdó maximális!
 +
*''A rezonanciafrekvencia – különösen nagy csillapítás esetében – eltér a sajátfrekvenciától.''
 +
*''Amennyiben a rezgések amplitúdója túl nagy vagy túl kicsi lenne, úgy kapcsolja ki a készüléket és csökkentse, illetve növelje a kényszererő amplitúdóját, majd ellenőrizze a kitérést a rezonanciafrekvenciánál!''
  
−
Amennyiben mindent rendben talál, vegye fel táblázatosan a rezonanciafrekvenciánál 1 Hz-el kisebb és 1 Hz-el nagyobb frekvenciák közötti intervallumban 0,1 Hz-enként (és a rezonancia frekvencia közelében ennél sűrűbben is) a kitérési amplitúdókat! Ábrázolja az azonos tömeggel, de különböző csillapítással felvett görbéket közös diagrammon! Adja meg minden esetben $f_{\text{max}}$ értékét!
+
Amennyiben mindent rendben talál, vegye fel táblázatosan a rezonanciafrekvenciánál 1 Hz-cel kisebb és 1 Hz-cel nagyobb frekvenciák közötti intervallumban 0,1 Hz-enként (és a rezonancia frekvencia közelében ennél sűrűbben is) a kitérési amplitúdókat! Ábrázolja a különböző csillapítással felvett görbéket közös diagrammon! Adja meg minden esetben $f_{max}$ értékét!
  
−
A korábban megmért görbék valamennyi pontjánál (a kitérési amplitúdó és frekvencia ismeretében) számítsa ki a sebeség-amplitúdó $(A\cdot 2\pi f=A\omega)$ értékeket! Foglalja táblázatba és ábrázolja diagrammon a sebesség-amplitúdó - frekvencia görbéket!
+
A korábban megmért görbék valamennyi pontjánál (a kitérési amplitúdó és frekvencia ismeretében) számítsa ki a sebeségamplitúdó $(A\cdot 2\pi f=A\omega)$ értékeket! Foglalja táblázatba és ábrázolja diagrammon a sebességamplitúdó – körfrekvencia görbéket!
 +
*''A különböző csillapítással felvett görbéket most is közös diagrammon ábrázolja!
  
 
'''4.''' Csillapítási tényező és jósági tényező meghatározása
 
'''4.''' Csillapítási tényező és jósági tényező meghatározása
  
−
A csillapítási tényező kísérleti meghatározásának egyik lehetséges módszere a [[#eq:3|(3)]] egyenleten alapul. Ekkor egymás utáni lengések amplitúdó csökkenéseit mérjük. Ennek észlelése akkor pontos, ha a lengő rendszer periódusideje eléggé nagy (kb. 3<sup>&minus;10</sup>s). Az alkalmazott rugónál a lengésidő rövidebb, emiatt egy másik módszer alkalmazása előnyösebb. A csillapítási- és jósági tényezők a sebesség-amplitúdó frekvenciafüggéséből meghatározhatók. A sebesség-amplitúdó kifejezése:
+
A csillapítási tényező kísérleti meghatározásának egyik lehetséges módszere a csillapodási hányados mérésén alapul. Ekkor egymás utáni lengések amplitúdócsökkenéseit mérjük. Ennek észlelése akkor pontos, ha a lengő rendszer periódusideje eléggé nagy (kb. 3-10 s). Az alkalmazott rugónál a lengésidő rövidebb, emiatt egy másik módszer alkalmazása előnyösebb: a csillapítási- és jósági tényezők a sebességamplitúdó frekvenciafüggéséből meghatározhatók.
−
{{eq|A\omega{{=}}\frac{F\omega}{m\sqrt{(\omega_0^2-\omega^2)^2+4\delta^2\omega^2} },|eq:6|(6)}}
+
 
−
melynek maximuma $\omega_0$-nál van, ahol
+
Illesszen a 3. pontban mért sebességamplitúdó adatokra a sebességamplitúdó – körfrekvencia függvénynek megfelelő görbét! Az illesztett görbe illesztési paraméterei között szerepel a $\beta$ csillapítási tényező  és az $\omega_0$ saját körfrekvencia (valamint az $F_0/m$ hányados). Az illesztés alapján határozza meg ezeket a paramétereket és hibájukat. Ezek alapján már meghatározható a jósági tényező is.
−
$$A\omega_0=\frac{F_0}{m2\delta}.$$.
+
−
A maximum felének megfelelő frekvenciáknál ($f_1<f_2$, illetve $\omega_1<\omega_2$) $\omega_1$-nél
+
−
$$\frac{F_0}{4m\delta}=\frac{F_0\omega_1}{m\sqrt{(\omega_0^2-\omega_1^2)^2+4\delta^2\omega_1^2} },$$
+
−
$\omega_2$-nél
+
−
$$\frac{F_0}{4m\delta}=\frac{F_0\omega_2}{m\sqrt{(\omega_0^2-\omega_2^2)^2+4\delta^2\omega_2^2} }.$$
+
−
Négyzetre emelés és átrendezés után $(\omega_0^2-\omega_1^2)=\delta\omega_1\sqrt{12}$ ill. $(\omega_0^2+\omega_2^2)=\delta\omega_2\sqrt{12}$ adódik, míg $\delta$-t behelyettesítve $\omega_0=\sqrt{\omega_1\omega_2}$ $[f_0=\sqrt{f_1f_2}]$. Ezek alapján a $\delta$ csillapítási tényező
+
−
{{eq|\delta{{=}}\frac{\omega_2-\omega_1}{\sqrt{12} }{{=}}\frac{2\pi(f_2-f_1)}{\sqrt{12} },|eq:7|(7)}}
+
−
míg a $Q$ jósági tényező  
+
−
{{eq|Q{{=}}\frac{\omega_0}{2\delta}{{=}}\frac{\sqrt{3f_1f_2} }{f_2-f_1}.|eq:8|(8)}}
+
−
Illesszen a [[#Kényszerrezgés amplitúdójának és sebesség-amplitúdójának vizsgálata a kényszerítő frekvencia függvényében|3. pontban]] mért sebességamplitúdó adatokra a [[#eq:6|(6)]] egyenletnek megfelelő görbét és határozza meg a maximális sebesség-amplitúdó értékét, majd állapítsa meg azt a két frekvenciát melyeknél sebesség-amplitúdó a maximális érték fele! Számítsa ki a [[#eq:7|(7)]] és [[#eq:8|(8)]] képletek segítségével a csillapítási és jósági tényezőket!
+
  
 
'''5.''' Lebegés vizsgálata
 
'''5.''' Lebegés vizsgálata
133. sor: 155. sor:
 
{{fig|A_kényszerrezgés_vizsgálata_5.png|fig:5|5. ábra}}
 
{{fig|A_kényszerrezgés_vizsgálata_5.png|fig:5|5. ábra}}
  
−
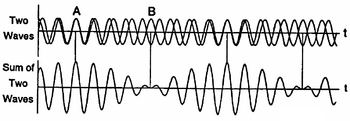
Két, kis mértékben különböző frekvenciájú, szinusz-hullám szuperpozíciójakor "lebegés" alakul ki [[#fig:5|(5. ábra)]]. Ha $t_A$ időpontban a rezgések éppen fázisban vannak, akkor a hullámok összeadódnak és az eredő rezgés maximális amplitúdójú lesz. Egy későbbi $t_B$ időpontban azonban a frekvencia különbség miatt a rezgések ellentétes fázisba kerülnek, és egymás hatását csökkentve minimális amplitúdót eredményeznek. Az amplitúdó változások burkológörbéje szintén szinuszos. A burkológörbe frekvenciája $f_L=\frac{f_1-f_2}{2}$, ahol $f_1$ és $f_2$ a két összetevő rezgés frekvenciája. A differenciálegyenlet megoldása [[#eq:4|(4)]] képlet tartalmazza a bekapcsolás után kialakuló két fajta frekvenciát. Az egyik szinusz-hullám körfrekvenciája $\omega’$, a másiké $\omega$. Lebegés akkor figyelhető meg, ha a kényszererő $\omega$ körfrekvenciája $\omega’$ közelében van, valamint, ha a csillapodás kicsi. Amint a tranziens elhal, a lebegés is megszűnik.  
+
Két, kis mértékben különböző frekvenciájú, szinuszhullám szuperpozíciójakor „lebegés” alakul ki [[#fig:5|(5. ábra)]]. Ha $t_A$ időpontban a rezgések éppen fázisban vannak, akkor a hullámok összeadódnak és az eredő rezgés maximális amplitúdójú lesz. Egy későbbi $t_B$ időpontban azonban a frekvencia különbség miatt a rezgések ellentétes fázisba kerülnek, és egymás hatását csökkentve minimális amplitúdót eredményeznek. Az amplitúdó változások burkológörbéje szintén szinuszos. A burkológörbe frekvenciája $f_L=\left(f_1-f_2\right)/2$, ahol $f_1$ és $f_2$ a két összetevő rezgés frekvenciája.
 +
 
 +
A kényszerrezgés bekapcsolásakor az állandósult tag mellett egy darabig megfigyelhető a csillapított rendszer idővel elhaló saját rezgése is. A differenciálegyenlet megoldása tartalmazza a bekapcsolás után kialakuló mindkét frekvenciát. A tranziens rezgés körfrekvenciája $\omega’$, az állandósulté pedig $\omega$. Lebegés akkor figyelhető meg, ha a kényszererő $\omega$ körfrekvenciája $\omega’$ közelében van, és a csillapítás elég kicsi. Amint a tranziens elhal, a lebegés is megszűnik.
 +
 
 +
Szerelje le újra a csillapító mágnespofákat és állítsa be pontosan a mérőrúd helyzetét. Határozza meg a rendszer sajátfrekvenciáját! (A 2. méréshez hasonlóan használja a készülék kijelzőjén a PERIOD állást! $f_0=1/T$) Állítsa a kényszerkeréken az amplitúdót 2 mm-re! Kapcsolja be a kényszermozgást és szabályozza annak frekvenciáját úgy, hogy 0,1 Hz-cel legyen alacsonyabb, mint $f_0$! Jegyezze fel mindét frekvencia értékét és kapcsolja ki a kényszert! Várjon, amíg a mérőrúd megáll! Állítsa a funkciókapcsolót AMPL. állásba.
 +
 
 +
Helyezze a mérőrúd alá az ultrahangos érzékelőt! Indítsa el a számítógépen a ''Logger Lite'' programot. A program felismeri a rákapcsolt szenzort. Végezze el a következő beállításokat: ''Experiment $\to$ Data Collection $\to$ Length'': 120 s; ''Options $\to$ Graph Options $\to$ Axes Options $\to$ Scaling: Autoscale'' (mindkét tengelyen).
 +
 
 +
Indítsa el az adatgyűjtést, majd kapcsolja be a kényszerrezgést! A lebegés megszűntéig mérjen! Utána a mérési adatok a ''File $\to$ Export as'' paranccsal menthetők.  
  
−
Szerelje le újra a csillapító mágnespofákat és állítsa be pontosan a mérőrúd helyzetét. Határozza meg a rendszer sajátfrekvenciáját! (A [[#Csillapítatlan rendszer lengésideje|2. méréshez]] hasonlóan használja a készülék kijelzőjén a ''PERIÓDUS'' állást! $f_0=\frac{1}{T}$) Állítsa a kényszerkeréken az amplitúdót 2 mm-re! Kapcsolja be a kényszermozgást és szabályozza annak frekvenciáját úgy, hogy 0,1 Hz-el legyen alacsonyabb, mint $f_0$! Jegyezze fel mindét frekvencia értékét és kapcsolja ki a kényszert! Várjon, amíg a mérőrúd megáll! Állítsa a funkciókapcsolót ''AMPLITÚDÓ'' mérésre.
+
Ábrázolja az amplitúdót az idő függvényében! Határozza meg a burkoló szinuszgörbe periódusidejét és frekvenciáját!
 +
*''Vesse össze az elmélet alapján várható értékekkel!''
 +
*''Akkor kap szép lebegést, ha kicsi a csillapítás (leszedett mágnespofák, jól beállított mérőrúd (nem súrlódik).''
  
−
Helyezze a mérőrúd alá az ultrahangos érzékelőt! Indítsa el a számítógépen a Logger Lite programot. A program felismeri a rákapcsolt szenzort. Végezze el a következő beállításokat: ''Experiment - Data Collection - Length'': 120 s; ''Options - Graph Options - Axes Options - Scaling: Autoscale'' (mindkét tengelyen).
+
'''FONTOS!''' Ebből a mérésból és az [[RLC körök mérése|RLC körök méréséből]] '''közös jegyzőkönyvet''' kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!
  
−
Indítsa el az adatgyűjtést, majd kapcsolja be a kényszerrezgést! A lebegés megszűntéig mérjen! Utána a mérési adatok a ''File- Export'' as paranccsal menthetők.
 
  
−
Ábrázolja az amplitúdót az idő függvényében! Határozza meg a burkoló szinusz-görbe periódusidejét és frekvenciáját! Vesse össze az elmélet alapján várható értékekkel!
+
[[Fizika laboratórium 1.|Vissza a Fizika laboratórium 1. tárgyoldalára.]]
  
 
</wlatex>
 
</wlatex>

A lap jelenlegi, 2020. február 29., 23:02-kori változata


A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul.

Ebben a mérésben mechanikai rezgéseket fog tanulmányozni. Az ezzel teljesen analóg módon leírható elektromos rezgőköröket az RLC körök mérésében tanulmányozza. A két mérésből közös jegyzőkönyvet kell készítenie.


Tartalomjegyzék


Elméleti összefoglaló

Csillapítatlan rezgések

Ha egy \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömegű anyagi pontra a kitéréssel arányos, rugalmas erő hat, akkor a mozgásegyenlet

\[ma=-Dx\]

alakú, ahol \setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0% a rugóállandó, \setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0% a tömegpont kitérése az egyensúlyi helyzetből, \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% a tömeg, és \setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0% a gyorsulás. A mozgásegyenlet megoldása

\[x(t)=A\sin(\omega_0 t+\alpha)\]

ahol \setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0% a (kitérési) amplitúdó, \setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0% a \setbox0\hbox{$t=0$}% \message{//depth:\the\dp0//}% \box0% időpillanathoz tartozó fázis (mindkettőt a kezdeti feltételek határozzák meg),

\[\omega_0=\sqrt{\frac{D}{m}}\]

a csillapítatlan rezgő rendszer körfrekvenciája. (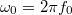\setbox0\hbox{$\omega_0=2\pi f_0$}% \message{//depth:\the\dp0//}% \box0%, ahol \setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0% a megfelelő frekvencia.)

A harmonikus rezgőmozgás sebessége

\[v(t)=\frac{\text{d} x}{\text{d} t}=A\omega_0\cos(\omega_0 t+\alpha)\]

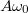ahol \setbox0\hbox{$A\omega_0$}% \message{//depth:\the\dp0//}% \box0% a maximális sebesség, az ún. sebességamplitúdó.

Csillapodó rezgések

A csillapodást okozó erők gyakran (jó közelítéssel) a sebességgel arányosak: 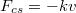\setbox0\hbox{$F_{cs}=-kv$}% \message{//depth:\the\dp0//}% \box0%, ahol \setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0% a csillapítás erősségére jellemző mennyiség. Ekkor a tömegpont mozgásegyenlete:

\[ma=-Dx-kv\]

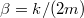ami a \setbox0\hbox{$\beta=k/(2m)$}% \message{//depth:\the\dp0//}% \box0% csillapítási tényező bevezetésével és \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0% definíciójának felhasználásával az alábbi alakra hozható:

\[\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=0\]

A differenciálegyenlet megoldása 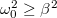\setbox0\hbox{$\omega_0^2\geq\beta^2$}% \message{//depth:\the\dp0//}% \box0% esetén időben csökkenő amplitúdójú lengéseket eredményez:

\[x(t)=Ae^{-\beta t}\sin(\omega' t+\alpha)\]

A rezgés körfrekvenciája

\[\omega'=\sqrt{\omega_0^2-\beta^2}\]

Az amplitúdóváltozás jellemzésére különböző mennyiségeket használnak. A csillapodási hányados két, azonos irányban egymás után következő amplitúdó hányadosa

\[K=\frac{x_n}{x_{n+1} }=e^{\beta T}\]

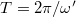ahol \setbox0\hbox{$T=2\pi/\omega'$}% \message{//depth:\the\dp0//}% \box0%. Használatos még a K csillapodási hányados logaritmusa, az ún. logaritmikus dekrementum is:

\[\Lambda=\ln K=\beta T\]

Kényszerrezgések

Egy \setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0% tömegre pl. motor és excenter segítségével időben periodikusan változó erőt alkalmazva egy átmeneti időszak után időben állandósult rezgés alakul ki, melynek frekvenciája megegyezik a kényszerítő erő frekvenciájával, míg amplitúdója függ az erőtől, a rugóállandótól, a tömegtől, a csillapítástól valamint a gerjesztő frekvenciától. Az anyagi pont mozgásegyenlete ekkor:

\[ma=-Dx-kv+F_0\sin(\omega t)\]

A korábban bevezetett jelöléseket alkalmazva másodrendű lineáris, inhomogén differenciálegyenletet kapunk:

\[\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=\frac{F_0}{m}\sin(\omega t)\]

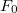ahol \setbox0\hbox{$F_0$}% \message{//depth:\the\dp0//}% \box0% a kényszererő maximális értéke. Az egyenlet megoldása:

\[x(t)=A_0e^{-\beta t}\sin(\omega' t+\alpha)+\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} }\sin(\omega t+\varphi),\]

melynek második tagja írja le az állandósult állapotot. Az állandósult állapot amplitúdója:

\[A(\omega)=\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} },\]

melynek maximuma van az

\[\omega_{max}=\sqrt{\omega_0^2-2\beta^2}\]

körfrekvenciánál. A \setbox0\hbox{$\varphi$}% \message{//depth:\the\dp0//}% \box0% fázisállandó nem az időmérés kezdetétől függ, hanem a kényszerítő erő fázisától való eltérés, ennek tangense:

\[\text{tg}\varphi=\frac{2\beta\omega}{\omega_0^2-\omega^2}.\]

Az amplitúdóhoz hasonlóan megadhatjuk a sebességamplitúdó kifejezését is:

\[A\omega=\frac{F_0\omega}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}}\]

melynek maximuma – ellentétben a kitérési amplitúdó maximumával – éppen \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%-nál van, ahol

\[A\omega_0=\frac{F_0}{2m\beta}.\]

A kényszerrezgés energiaviszonyainak jellemezésére az egy periódus alatt disszipált energia 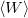\setbox0\hbox{$\langle W\rangle$}% \message{//depth:\the\dp0//}% \box0% és a rendszerben tárolt átlagos energia 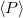\setbox0\hbox{$\langle P\rangle$}% \message{//depth:\the\dp0//}% \box0% hányadosával arányos jósági tényezőt használjuk

\[Q=2\pi\frac{\langle W\rangle}{T\langle P\rangle}\approx\frac{\omega_0}{2\beta}\]

A kísérleti berendezés leírása

1. ábra

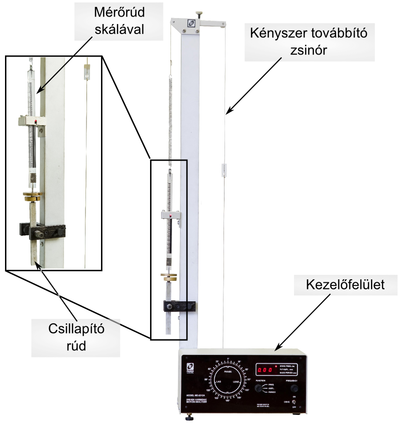
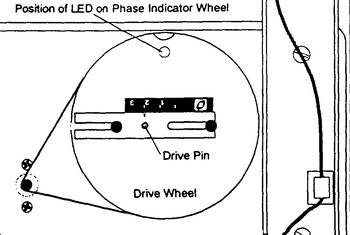
A kísérleti berendezés az 1. ábrán látható. Az alul elhelyezkedő elektronikai egység hátsó lapján található a kényszererőt létrehozó excenter. A kényszererő amplitúdója az amplitúdórúd helyzetének változtatásával szabályozható, ami a kényszert kifejtő zsinór rögzítési pontja és az excenter középpontja közötti távolságot befolyásolja (2. ábra). A kényszert továbbító zsinór a tartóoszlop tetején található két csiga vájatain áthaladva egy hurokkal kapcsolódik a vizsgálandó rugó egyik végéhez. A másik véghez a skálával ellátott mérőrúd és a hozzá erősített ún. csillapító rúd csatlakozik. E két rúd alkotja a rezgőmozgást végző „alaptömeget”, melynek értéke 50 g.

A mérőkészlethez tartozik két 50 g tömegű rézkorong is. A korongokat a mérőrudat és csillapitórudat összekötő csavarmenetre lehet felerősíteni. A tartóoszlop középmagasságánál látható a rúdvezető, melyben optikai érzékelők vannak. A mérőrudat a rúdvezető téglalap alakú nyílásán kell átvezetni.

Helyes beállítás esetén a rezgés csillapodása – melyet a légellenállás ill. a berendezés egyes elemei között fellépő súrlódás okoz – igen kicsi. Ezért a csillapítás változtatása (növelése) céljából a tartórúdra egy olyan mágnespárt szerelhetünk fel, melynek pofái között a távolság változtatható. Ezen mágnespofák között mozog az alumíniumból készült csillapítórúd. A mágneses tér hatására a mozgó fémrúdban örvényáramok keletkeznek, melyek Joule-hőjének disszipációja okozza a rendszer csillapodását. A mágnespofák közötti távolság csökkentésével a mágneses térerősség növelhető, azaz a disszipáció, vagyis a csillapítás fokozható.

Beállítás

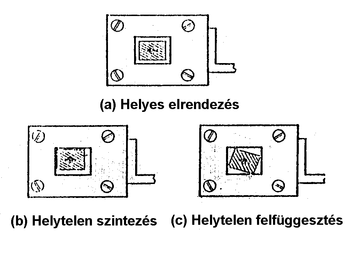
  • Ha a készülék jól van beállítva, a mérőrúd úgy függ, hogy egyik oldala sem ér hozzá a rúdvezető nyílásának falához (3. ábra). A nem jó a beállítás a 3. ábrán látható „b” vagy „c” esetben fordul elő. A „b” esetet az elektronika doboz változtatható magasságú lábainak megfelelő állításával korrigálhatjuk (vízszintezés). A „c” eset a mérőrúd felfüggesztésével (elcsavarásával)javítható.
  • A fázis és amplitúdó pontos méréséhez úgy kell felfüggeszteni a mérőrudat, hogy egyensúlyi helyzetben középvonala egybeessen a rúdvezető optikai érzékelőjével. Ennek beállításához:
    • Kapcsolja be az elektronika doboz hátoldalán levő kapcsolót. Figyelje a rúdvezető LED-et. Ha a mérőrúd középvonala (8,5 cm) feljebb van, mint a rúdvezető felső éle, akkor a LED kialszik. Ha a középvonal lejjebb került, akkor a LED kigyullad.
    • Mozgassa úgy a mérőrudat fel és le, hogy a középvonala áthaladjon a rúdvezetőn. Közben figyelje a FÁZIS kijelzést. Amikor a mérőrúd középvonala lefelé halad keresztül a rúdvezetőn, egy LED villog a fázisskálán. Annyira fordítsa el a kényszerkereket, hogy a fázist jelző LED éppen 0° fázishelyzetet mutasson.
    • Most pontosítsa a zsinór hosszát. Ez a zsinóron található plasztikcsattal állítható. Finom állítások a tartóoszlop tetején levő csavarral végezhetők. A zsinórhossz akkor megfelelő, ha egészen kicsi oszcillációknál a fázis LED ki-be kapcsol.

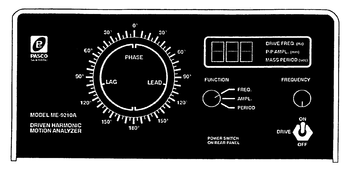
Az elektronika doboz a 4. ábrán látható. Az elülső lapon található a DRIVE kapcsoló. Ezzel indítható a motor, mely a kényszer kereket forgatja. A FREQUENCY gombbal változtatható a kényszer frekvenciája. Óramutató járásával megegyezően forgatva növeli a frekvenciát. A FUNCTION kapcsoló határozza meg azt, hogy az alábbi három változóból melyiket írja ki a digitális kijelző. (A kijelző jobb oldalán egy LED mutatja, hogy melyik változó értéket olvashatjuk le.)

  • FREQ. – A kényszerkerék frekvenciája (Hz)
  • AMPL. – A mérőrúd csúcstól-csúcsig amplitúdója (ez az amplitúdó kétszerese) (mm)
  • PERIOD – A mérőrúd egy teljes rezgésének periódusideje (s).
2. ábra
3. ábra
4. ábra


Mérési feladatok

A méréshez rendelkezésre álló eszközök

  • A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.

1. A rugóállandó mérése

Állítsa be a zsinór hosszát úgy, hogy a mérőrúd 17 cm-es jele a rúdvezető alsó szélével egy vonalba essék! Erősítse az egyik 50 g-os rézsúlyt a mérőrúd és a csillapítórúd közé! Mérje le a rugó sztatikus megnyúlását! Ezután helyezze fel a második rézsúlyt is, és mérje meg az újabb megnyúlást! Számítsa ki a rugó rugóállandóját!

2. Csillapítatlan rendszer lengésideje

Szabályozza be a készüléket!

  • Nagyon fontos, hogy a mérőrúd ne érjen a rúdvezető egyik falához se (lásd az előző pontban)!

Ehhez a méréshez szerelje le a csillapító mágnespofákat! A funkciókapcsolót állítsa periódusidőmérésre (PERIOD). Húzza a mérőrudat kb. 5 cm-rel az egyensúlyi helyzete alá, és engedje el! A digitális kijelző ekkor a rezgés periódusidejét (s) mutatja. A mérést üres mérőrúddal, majd 50 és 100 g-os terhelésekkel is végezze el!

  • Az eredményeket foglalja táblázatba és vesse össze az elmélet alapján kiszámolt értékekkel!

3. Kényszerrezgés amplitúdójának és sebességamplitúdójának vizsgálata a kényszerítő frekvencia függvényében

A méréseket két különböző csillapítás esetén, mérőrúd + 50 g tömeggel végezze el! Szerelje vissza a csillapító mágnespofákat! A kis csillapításhoz a csillapító mágnespofákat egymástól a lehető legtávolabb állítsa be! A nagy csillapításhoz tekerje a mágnespofákat a lehető legközelebb, de csak annyira, hogy ne érjenek hozzá a csillapítórúdhoz! Ekkor mérje meg és jegyezze fel a mágnespofák távolságát!

Gondosan állítsa be a mérőrúd helyzetét úgy, hogy már egészen kis kitéréseknél villogjon a digitális kijelző (beállítás)! A funkciókapcsolót állítsa frekvenciamérésre (FREQ.) és a DRIVE kapcsolóval indítsa el a kényszerrezgést! A frekvenciaszabályozó gombbal lassan (fokozatosan) növelje a frekvenciát, és időről-időre váltson át az amplitúdómérésre (AMPL.)!

  • Itt a kijelző mm-ben megadja a csúcstól-csúcsig amplitúdót – ez az amplitúdó kétszerese.
  • Figyelje eközben a fázisállandót jelző LED értékét is! Amikor a kényszerítő frekvencia megegyezik az \setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0% sajátfrekvenciával, a fázisszög 90°.

Keresse meg az 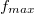\setbox0\hbox{$f_{max}$}% \message{//depth:\the\dp0//}% \box0% rezonanciafrekvenciát, ahol az amplitúdó maximális!

  • A rezonanciafrekvencia – különösen nagy csillapítás esetében – eltér a sajátfrekvenciától.
  • Amennyiben a rezgések amplitúdója túl nagy vagy túl kicsi lenne, úgy kapcsolja ki a készüléket és csökkentse, illetve növelje a kényszererő amplitúdóját, majd ellenőrizze a kitérést a rezonanciafrekvenciánál!

Amennyiben mindent rendben talál, vegye fel táblázatosan a rezonanciafrekvenciánál 1 Hz-cel kisebb és 1 Hz-cel nagyobb frekvenciák közötti intervallumban 0,1 Hz-enként (és a rezonancia frekvencia közelében ennél sűrűbben is) a kitérési amplitúdókat! Ábrázolja a különböző csillapítással felvett görbéket közös diagrammon! Adja meg minden esetben 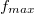\setbox0\hbox{$f_{max}$}% \message{//depth:\the\dp0//}% \box0% értékét!

A korábban megmért görbék valamennyi pontjánál (a kitérési amplitúdó és frekvencia ismeretében) számítsa ki a sebeségamplitúdó 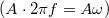\setbox0\hbox{$(A\cdot 2\pi f=A\omega)$}% \message{//depth:\the\dp0//}% \box0% értékeket! Foglalja táblázatba és ábrázolja diagrammon a sebességamplitúdó – körfrekvencia görbéket!

  • A különböző csillapítással felvett görbéket most is közös diagrammon ábrázolja!

4. Csillapítási tényező és jósági tényező meghatározása

A csillapítási tényező kísérleti meghatározásának egyik lehetséges módszere a csillapodási hányados mérésén alapul. Ekkor egymás utáni lengések amplitúdócsökkenéseit mérjük. Ennek észlelése akkor pontos, ha a lengő rendszer periódusideje eléggé nagy (kb. 3-10 s). Az alkalmazott rugónál a lengésidő rövidebb, emiatt egy másik módszer alkalmazása előnyösebb: a csillapítási- és jósági tényezők a sebességamplitúdó frekvenciafüggéséből meghatározhatók.

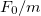Illesszen a 3. pontban mért sebességamplitúdó adatokra a sebességamplitúdó – körfrekvencia függvénynek megfelelő görbét! Az illesztett görbe illesztési paraméterei között szerepel a \setbox0\hbox{$\beta$}% \message{//depth:\the\dp0//}% \box0% csillapítási tényező és az \setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0% saját körfrekvencia (valamint az \setbox0\hbox{$F_0/m$}% \message{//depth:\the\dp0//}% \box0% hányados). Az illesztés alapján határozza meg ezeket a paramétereket és hibájukat. Ezek alapján már meghatározható a jósági tényező is.

5. Lebegés vizsgálata

5. ábra

Két, kis mértékben különböző frekvenciájú, szinuszhullám szuperpozíciójakor „lebegés” alakul ki (5. ábra). Ha 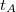\setbox0\hbox{$t_A$}% \message{//depth:\the\dp0//}% \box0% időpontban a rezgések éppen fázisban vannak, akkor a hullámok összeadódnak és az eredő rezgés maximális amplitúdójú lesz. Egy későbbi 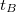\setbox0\hbox{$t_B$}% \message{//depth:\the\dp0//}% \box0% időpontban azonban a frekvencia különbség miatt a rezgések ellentétes fázisba kerülnek, és egymás hatását csökkentve minimális amplitúdót eredményeznek. Az amplitúdó változások burkológörbéje szintén szinuszos. 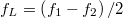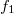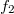A burkológörbe frekvenciája \setbox0\hbox{$f_L=\left(f_1-f_2\right)/2$}% \message{//depth:\the\dp0//}% \box0%, ahol \setbox0\hbox{$f_1$}% \message{//depth:\the\dp0//}% \box0% és \setbox0\hbox{$f_2$}% \message{//depth:\the\dp0//}% \box0% a két összetevő rezgés frekvenciája.

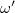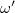A kényszerrezgés bekapcsolásakor az állandósult tag mellett egy darabig megfigyelhető a csillapított rendszer idővel elhaló saját rezgése is. A differenciálegyenlet megoldása tartalmazza a bekapcsolás után kialakuló mindkét frekvenciát. A tranziens rezgés körfrekvenciája \setbox0\hbox{$\omega’$}% \message{//depth:\the\dp0//}% \box0%, az állandósulté pedig \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%. Lebegés akkor figyelhető meg, ha a kényszererő \setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0% körfrekvenciája \setbox0\hbox{$\omega’$}% \message{//depth:\the\dp0//}% \box0% közelében van, és a csillapítás elég kicsi. Amint a tranziens elhal, a lebegés is megszűnik.

Szerelje le újra a csillapító mágnespofákat és állítsa be pontosan a mérőrúd helyzetét. Határozza meg a rendszer sajátfrekvenciáját! (A 2. méréshez hasonlóan használja a készülék kijelzőjén a PERIOD állást! 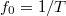\setbox0\hbox{$f_0=1/T$}% \message{//depth:\the\dp0//}% \box0%) Állítsa a kényszerkeréken az amplitúdót 2 mm-re! Kapcsolja be a kényszermozgást és szabályozza annak frekvenciáját úgy, hogy 0,1 Hz-cel legyen alacsonyabb, mint \setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0%! Jegyezze fel mindét frekvencia értékét és kapcsolja ki a kényszert! Várjon, amíg a mérőrúd megáll! Állítsa a funkciókapcsolót AMPL. állásba.

Helyezze a mérőrúd alá az ultrahangos érzékelőt! Indítsa el a számítógépen a Logger Lite programot. A program felismeri a rákapcsolt szenzort. Végezze el a következő beállításokat: Experiment \setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0% Data Collection \setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0% Length: 120 s; Options \setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0% Graph Options \setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0% Axes Options \setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0% Scaling: Autoscale (mindkét tengelyen).

Indítsa el az adatgyűjtést, majd kapcsolja be a kényszerrezgést! A lebegés megszűntéig mérjen! Utána a mérési adatok a File \setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0% Export as paranccsal menthetők.

Ábrázolja az amplitúdót az idő függvényében! Határozza meg a burkoló szinuszgörbe periódusidejét és frekvenciáját!

  • Vesse össze az elmélet alapján várható értékekkel!
  • Akkor kap szép lebegést, ha kicsi a csillapítás (leszedett mágnespofák, jól beállított mérőrúd (nem súrlódik).

FONTOS! Ebből a mérésból és az RLC körök méréséből közös jegyzőkönyvet kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!


Vissza a Fizika laboratórium 1. tárgyoldalára.


A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=A_kényszerrezgés_vizsgálata&oldid=26330”