„Lencsehibák vizsgálata sugárkövetés módszerével” változatai közötti eltérés
Gall (vitalap | szerkesztései) |
Lenk (vitalap | szerkesztései) a |
||
| (2 szerkesztő 340 közbeeső változata nincs mutatva) | |||
| 17. sor: | 17. sor: | ||
<!--[[Kategória:Fizika laboratórium 4.]]--> | <!--[[Kategória:Fizika laboratórium 4.]]--> | ||
[[Kategória:Fizika laboratórium 5.]] | [[Kategória:Fizika laboratórium 5.]] | ||
| − | [[Kategória:Szerkesztő:Gáll | + | [[Kategória:Szerkesztő:Gáll]] |
| + | [[Kategória:Szerkesztő:Lenk]] | ||
__TOC__ | __TOC__ | ||
| − | |||
| − | |||
==Elméleti összefoglaló== | ==Elméleti összefoglaló== | ||
| 27. sor: | 26. sor: | ||
===Bevezetés=== | ===Bevezetés=== | ||
| − | + | A személyi számítógépek tömeges elterjedése sok más klasszikus tudományterület mellett a fizika, ezen belül a geometriai optika módszereit is gyökeresen megváltoztatta. A zárt formulák és képletek helyett széles körben elterjedtek a numerikus módszerek. Számítógépek alkalmazásával kiküszöbölhető a geometriai optikával együtt járó algebrai számítások nagy része, és a számítási eredmények szemléletesen meg is jeleníthetők a képernyőn. Interaktív programok alkalmazásával lehetőség van számítógépes kísérleteket végezni és összetett lencserendszereket tervezni, optimalizálni. | |
| − | A személyi számítógépek tömeges elterjedése sok más klasszikus tudományterület mellett a fizika, ezen belül a geometriai optika módszereit is gyökeresen megváltoztatta. A zárt formulák és képletek helyett széles körben elterjedtek a numerikus módszerek. Számítógépek alkalmazásával kiküszöbölhető a geometriai optikával együtt járó algebrai számítások nagy része, és a számítási eredmények szemléletesen meg is jeleníthetők a képernyőn. Interaktív programok alkalmazásával lehetőség van számítógépes kísérleteket | + | |
Jelen mérés is egy ilyen grafikus, interaktív, számítógépes kísérletezésre alkalmas programra mutat példát, amely az áthaladó fénysugarak valós (nem csak az elsőrendben közelített, ú.n. paraxiális) menetét határozza meg. A mérésben használt program egy lencsetervező rendszer, amely alkalmas az optikai rendszerek részletes analízisére, és optimalizálására. A mérés során a program nyújtotta szolgáltatások közül csak a sugárátvezetést és a grafikus megjelenítést használjuk ki. Az optikai rendszerek részletes analízise, és az optimalizálás messze meghaladja egy alap fizika laboratórium kereteit (ezt az Optikai rendszerek tervezése c. választható tárgy keretei között sajátíthatják el). | Jelen mérés is egy ilyen grafikus, interaktív, számítógépes kísérletezésre alkalmas programra mutat példát, amely az áthaladó fénysugarak valós (nem csak az elsőrendben közelített, ú.n. paraxiális) menetét határozza meg. A mérésben használt program egy lencsetervező rendszer, amely alkalmas az optikai rendszerek részletes analízisére, és optimalizálására. A mérés során a program nyújtotta szolgáltatások közül csak a sugárátvezetést és a grafikus megjelenítést használjuk ki. Az optikai rendszerek részletes analízise, és az optimalizálás messze meghaladja egy alap fizika laboratórium kereteit (ezt az Optikai rendszerek tervezése c. választható tárgy keretei között sajátíthatják el). | ||
A geometriai optika középiskolából ismert egyszerű közelítő eljárásai (ld. pl. lencsetörvény) csak az optikai tengelyhez közeli tárgy-kép pontokra, és a tengellyel kis szöget bezáró paraxiálisnak nevezett sugarakra érvényesek (lásd pl. Budó-Mátrai: Kísérleti Fizika III. 35-76. oldal). A paraxiális közelítés hatalmas előnye abban rejlik, hogy keretei között teljesülnek az ideális képalkotást feltételei (többek között éles, torzításmentes az így kapott kép). A tengelytől távol haladó, valamint a tengellyel nagy szöget bezáró sugarak különböző képalkotási hibákat okoznak, mint pl. nyíláshiba (vagy gömbi eltérés), asztigmatizmus, kóma, képmezőhajlás. A lencsék anyagaként használt üvegek törésmutatójának hullámhossz függése (diszperziója) miatt fellép továbbá színi hiba (kromatikus aberráció) is. A felsorolt hibák pontos tárgyalása bonyolult és hosszadalmas. Jelen mérés célja ezen hibák kísérleti bemutatása a számítógép adta lehetőségek felhasználásával. (A hibák leírását lásd Budó-Mátrai: Kísérleti Fizika III. 65-69 oldal). | A geometriai optika középiskolából ismert egyszerű közelítő eljárásai (ld. pl. lencsetörvény) csak az optikai tengelyhez közeli tárgy-kép pontokra, és a tengellyel kis szöget bezáró paraxiálisnak nevezett sugarakra érvényesek (lásd pl. Budó-Mátrai: Kísérleti Fizika III. 35-76. oldal). A paraxiális közelítés hatalmas előnye abban rejlik, hogy keretei között teljesülnek az ideális képalkotást feltételei (többek között éles, torzításmentes az így kapott kép). A tengelytől távol haladó, valamint a tengellyel nagy szöget bezáró sugarak különböző képalkotási hibákat okoznak, mint pl. nyíláshiba (vagy gömbi eltérés), asztigmatizmus, kóma, képmezőhajlás. A lencsék anyagaként használt üvegek törésmutatójának hullámhossz függése (diszperziója) miatt fellép továbbá színi hiba (kromatikus aberráció) is. A felsorolt hibák pontos tárgyalása bonyolult és hosszadalmas. Jelen mérés célja ezen hibák kísérleti bemutatása a számítógép adta lehetőségek felhasználásával. (A hibák leírását lásd Budó-Mátrai: Kísérleti Fizika III. 65-69 oldal). | ||
| − | |||
| − | |||
===A sugárkövetés fizikai alapjai=== | ===A sugárkövetés fizikai alapjai=== | ||
| − | A sugárkövetés során a törési törvény sorozatos alkalmazására kerül sor. A számításokat a | + | A sugárkövetés során a törési törvény sorozatos alkalmazására kerül sor. A számításokat a [[#fig:1|11.1.ábra]] koordináta rendszerében végezzük. Gömbsüveg alakú lencsék, tükrök esetén az egyes törő-/ tükröző felületeket négy adattal jellemezzük: |
*- görbületi sugár (görbület ≡ 1 / görbületi sugár), | *- görbületi sugár (görbület ≡ 1 / görbületi sugár), | ||
*- a törőfelületet követő anyag törésmutatója, | *- a törőfelületet követő anyag törésmutatója, | ||
*- a törőfelületet követő felület távolsága, | *- a törőfelületet követő felület távolsága, | ||
*- a törőfelület apertúrájának (nyílásának) sugara | *- a törőfelület apertúrájának (nyílásának) sugara | ||
| − | (Ezt a számításnál általában nem használja a program, csak a rajz elkészítésénél). | + | (Ezt a számításnál általában '''nem''' használja a program, csak a rajz elkészítésénél). |
| − | {{fig|11.1. ábra.JPG|fig:1|11.1. ábra}} | + | {| cellpadding="5" cellspacing="0" align="center" |
| + | |- | ||
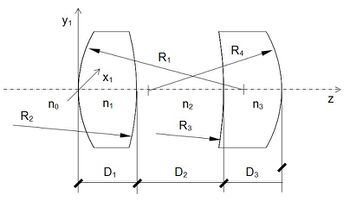
| + | | {{fig|11.1.1.ábra.JPG|fig:1|11.1. ábra. A felületen a fénytörést a felülethez rendelt lokális koordinátarendszerben vizsgáljuk (ld. az ábrán az első felületnél x<sub>1</sub>, y<sub>1</sub>), amelynek origója a felület és az optikai tengely metszéspontja. A szokásos konvenciónak megfelelően az ábrán feltüntetett első felület görbületi sugara (R<sub>1</sub>) pozitív, a másodiké (R<sub>2</sub>) negatív.}} | ||
| + | |} | ||
| − | + | Az abszolút koordináta-rendszer origója a tárgy és az optikai tengely metszéspontjában van. A ''z''-tengely egybeesik az optikai tengellyel. Az első törőfelület előtt a program automatikusan levegőt (n<sub>0</sub>=1 törésmutatót) tételez fel. Az utolsó törőfelület után - a felhasználó által megadott távolságban - a program automatikusan egy zérus görbületű felületet (sík ernyőt) tételez fel (képsík). | |
| − | Az abszolút koordináta-rendszer origója a tárgy és az optikai tengely metszéspontjában van. A z-tengely egybeesik az optikai tengellyel. Az első törőfelület előtt a program automatikusan levegőt ( | + | |
Egy fénysugarat a tér adott pontjában általános esetben hat adat ír le: | Egy fénysugarat a tér adott pontjában általános esetben hat adat ír le: | ||
| − | * | + | *X<sub>0</sub> : x koordináta, |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Az ( | + | *Y<sub>0</sub> : y koordináta, |
| − | + | ||
| − | (11.1 | + | *Z<sub>0</sub> : z koordináta, |
| − | A program a számításokat mindig egy lokális, az adott törőfelület és a z-tengely metszéspontjához rögzített koordináta-rendszerben végzi. Így a z koordináta értékeket ahol szükséges, át kell számolni abszolút koordinátákra. Az új közegben érvényes iránykoszinuszokat a 11.2. ábra alapján határozhatjuk meg. A számítások során a (11.2 | + | |
| − | 11.2. ábra. Az új közegben érvényes iránykoszinuszok meghatározása | + | *K : az x tengellyel bezárt szög koszinusza, |
| + | |||
| + | *L : az y tengellyel bezárt szög koszinusza, | ||
| + | |||
| + | *M : a z tengellyel bezárt szög koszinusza. | ||
| + | |||
| + | Az (X<sub>0</sub>, V<sub>0</sub>, Z<sub>0</sub>), a sugár kiinduló pontját, vagy egy törőfelülettel alkotott metszéspontját jelenti. (K, L, M) jelöli az iránykoszinuszokat (azaz a fénysugár irányú egységvektor koordinátáit), amelyek közül csak kettő független. A számítások során a program meghatározza a sugár metszéspontját a következő törőfelülettel, és a törési törvény alapján kiszámítja a sugár új irányát/iránykoszinuszait a következő közegben. A metszéspont meghatározása a ([[#eq:1|11.1]]) egyenletrendszer megoldását jelenti: | ||
| + | |||
| + | $$x = {{\rm{X}}_{\rm{0}}} + {\rm{K}}t$$ | ||
| + | $$y = {{\rm{Y}}_{\rm{0}}} + {\rm{L}}t$$ | ||
| + | $$z = {{\rm{Z}}_{\rm{0}}} + {\rm{M}}t$$ | ||
| + | {{eq|{{R^2} = {x^2} + {y^2} + {(z - R)^2}}|eq:1|(11.1)}} | ||
| + | |||
| + | A program a számításokat mindig egy lokális, az adott törőfelület és a ''z''-tengely metszéspontjához rögzített koordináta-rendszerben végzi. Így a ''z'' koordináta értékeket ahol szükséges, át kell számolni abszolút koordinátákra. Az új közegben érvényes iránykoszinuszokat a [[#fig:2|11.2.ábra]] alapján határozhatjuk meg. A számítások során a ([[#eq:2|11.2]]), ([[#eq:3|11.3]]) egyenletekből indulunk ki. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
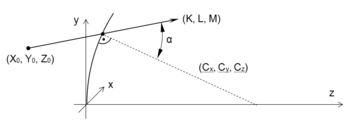
| + | | {{fig|Lencsehiba_2.png|fig:2|11.2. ábra. Az új közegben érvényes iránykoszinuszok meghatározása}} | ||
| + | |} | ||
| + | |||
| + | A beesési szög koszinusza a beeső nyaláb és a beesési pontba húzott felületi normális skaláris szorzatából számolható: | ||
| + | {{eq|C_xK + C_yL + C_zM {{=}} cos\alpha |eq:2|(11.2)}} | ||
| + | |||
| + | Itt (C<sub>x</sub>, C<sub>y</sub>, C<sub>z</sub>) a beesési pontba húzott felületnormális vektor iránykoszinuszait jelentik (lásd a [[#fig:2|11.2.ábrát]]). Az (C<sub>x</sub>, C<sub>y</sub>, C<sub>z</sub>) iránykoszinuszok a beesési pont meghatározása után számolhatók. A törési szög a Snellius-Descartes-törvényből számolható: | ||
| + | {{eq|\frac{\sin \alpha }{\sin \beta }{{=}}\frac{n_1}{n_0}{{=}}\sqrt {\frac{{1 - {\cos ^2}\alpha }}{{1 - {\cos ^2}\beta }}}|eq:3|(11.3)}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
Ebből az iránykoszinuszokra az alábbi egyenletet kapjuk: | Ebből az iránykoszinuszokra az alábbi egyenletet kapjuk: | ||
| − | + | {{eq|\frac{{1 - {\cos ^2}\alpha }}{{1 - {\cos ^2}\beta }} {{=}}\frac{n_1^2}{n_0^2}|eq:4|(11.4)}} | |
| − | + | {{eq|{(1 - {\cos ^2}\alpha )}\cdot \frac{n_0^2}{n_1^2} {{=}} 1 - {\cos ^2}\beta |eq:5|(11.5)}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | 11.3. ábra. A törési törvény felírásánál használt | + | Kifejezve ${\cos ^2}\beta $-t az alábbi egyenlet adódik: |
| + | |||
| + | {{eq|{\cos ^2}\beta {{=}} 1 + ( {\cos ^2}\alpha - 1 )\cdot \frac{n_0^2}{n_1^2}|eq:6|(11.6)}} | ||
| + | |||
| + | Kihasználjuk továbbá azt a tényt, hogy a beeső nyaláb, a megtört nyaláb és a beesési merőleges egy síkban fekszik, így a megtört nyaláb irányába mutató egységvektor felírható a beeső nyaláb <u>s</u><sub>0</sub>, és a beesési merőleges <u>s</u><sub>2</sub> egységvektorok lineáris kombinációjaként (lásd [[#fig:3|11.3.ábra]]). | ||
| + | {{eq|\underline s_1 {{=}} k{\underline s_0} + u{\underline s_2}|eq:7|(11.7)}} | ||
| + | |||
| + | A ([[#eq:7|11.7]]) egyenletet <u>s</u><sub>0</sub> -al, illetve <u>s</u><sub>2</sub> -vel beszorozva az alábbi két egyenletet nyerjük: | ||
| + | {{eq|{\underline s _0}{\underline s _1} {{=}} \cos \left( {\alpha - \beta } \right) {{=}} k + u\cos \alpha|eq:8|(11.8)}} | ||
| + | {{eq|\underline s _2\underline s _1 {{=}} \cos \beta {{=}} k\cos \alpha + u|eq:9|(11.9)}} | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
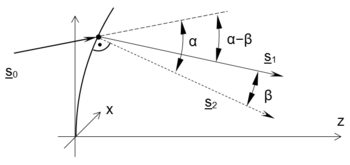
| + | | {{fig|Lencsehiba_3.png|fig:3|11.3. ábra. A törési törvény felírásánál használt koordinátarendszer}} | ||
| + | |} | ||
| + | |||
| + | A ([[#eq:8|11.8]]) és ([[#eq:9|11.9]]) egyenletekből a „k” és „u” ismeretlen paraméterek meghatározhatók: | ||
| + | {{eq|k{{=}}\frac{\sin \beta }{\sin \alpha }{{=}}\frac{n_0}{n_1}|eq:10|(10.10)}} | ||
| + | {{eq|{{u = \cos \beta - k \cdot \cos \alpha = \cos \beta \frac{{{{\rm{n}}_0}}}{{{{\rm{n}}_1}}} \cdot \cos \alpha}}|eq:11|(11.11)}} | ||
| − | |||
| − | |||
| − | |||
Ezek alapján a keresett egységvektor a következő egyenlet szerint írható le: | Ezek alapján a keresett egységvektor a következő egyenlet szerint írható le: | ||
| − | + | {{eq|\underline s _1 {{=}} k \cdot \underline s _0 + u \cdot \underline s _2 {{=}} \frac{n_0}{n_1} \underline s _0 + \frac{1}{n_1} \left(n_1 \cdot \cos \beta - n_0 \cdot \cos \alpha \right){\underline s _2}|eq:12|(11.12)}} | |
| − | A (11.12 | + | |
| − | + | A ([[#eq:12|11.12]]) vektoregyenlet három skalár egyenlet megoldását jelenti. Ezek megadják a megtört sugár (K', L', M') iránykoszinuszait. | |
| + | |||
| + | $${\underline s _1} = \left[ {\begin{array}{*{20}{c}} | ||
| + | {K'}\\ | ||
| + | {L'}\\ | ||
| + | {M'} | ||
| + | \end{array}} \right]$$ | ||
| + | {{eq||eq:13|(11.13)}} | ||
| + | |||
Ezek alapján a sugármenet számítására alkalmas program az alábbi számításokat végzi: | Ezek alapján a sugármenet számítására alkalmas program az alábbi számításokat végzi: | ||
| − | *- A belépő sugár (X<sub>0</sub>, Y<sub>0</sub>, Z<sub>0</sub>) kiinduló koordinátái és (K, L, M) iránykoszinuszai alapján a (11.1 | + | *- A belépő sugár (X<sub>0</sub>, Y<sub>0</sub>, Z<sub>0</sub>) kiinduló koordinátái és (K, L, M) iránykoszinuszai alapján a ([[#eq:1|11.1]]) egyenletrendszer megoldásával meghatározza a sugár és a felület (x, y, z) metszéspontját. |
| − | *- A (11.10), (11.11 ), (11.12 ) és (11.13) egyenletek alapján pedig kiszámítja a megtört sugár új iránykoszinuszait. | + | *- A ([[#eq:10|11.10]]), ([[#eq:11|11.11]]), ([[#eq:12|11.12]]) és ([[#eq:13|11.13]]) egyenletek alapján pedig kiszámítja a megtört sugár új iránykoszinuszait. |
A program a fenti két számítási lépést végzi el az összes belépő sugárra és az összes törőfelületre. Az eredmények numerikusan listázhatók, vagy különböző grafikus formákban megjeleníthetők. | A program a fenti két számítási lépést végzi el az összes belépő sugárra és az összes törőfelületre. Az eredmények numerikusan listázhatók, vagy különböző grafikus formákban megjeleníthetők. | ||
| − | |||
===Néhány szokásos elnevezés, definíció=== | ===Néhány szokásos elnevezés, definíció=== | ||
| + | *<u>Paraxiális sugarak:</u> az optikai tengellyel kis szöget bezáró (kb. 5° vagy kisebb, amelyekre teljesül $sin\alpha \approx \alpha [rad]$), és a tengelyhez közel haladó sugarak (x, y << R). | ||
| + | *<u>Paraxiális fókuszpont:</u> az optikai rendszer fókuszpontja végtelen távoli tárgypontból érkező paraxiális sugarak esetén. | ||
| + | *<u>Fősík:</u> paraxiális közelítésben az a két sík, amelyek m = +1-es nagyítású képei egymásnak. Ezek vékony lencse esetén egy síkká fajulnak, ami megegyezik a lencse síkjával. Tetszőlegesen bonyolult leképező rendszernél is meghatározható, és mindig csak kettő van belőle (első és hátsó). | ||
| + | *<u>Effektív fókusztávolság:</u> a paraxiális fókuszpont és a hátsó fősík „f” távolsága. Ha a „t” tárgytávolságot az első, a „k” képtávolságot pedig a hátsó fősíktól mérjük, akkor minden leképező rendszernél igaz a jól ismert lencsetörvény: $1/k = 1/f + 1/t$. | ||
| + | *<u>Apertúra:</u> magyarul nyílás. Ez lehet a lencse külső pereme, a lencsét tartó foglalat pereme, vagy egy külön erre a célra odahelyezett blende nyílása. | ||
| + | *<u>Tárgyszög:</u> a tárgytér szélén lévő tárgypontból az optikai rendszerhez érkező fénynyaláb központi fénysugarának az optikai tengellyel bezárt szöge. | ||
| + | *<u>Alaktényező:</u> | ||
| − | + | {{eq|S {{=}} \frac{R_1 + R_2}{R_1 - R_2}|eq:14|(11.14)}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
„S” egy-egy lencsetag jellemzője. Az összefüggés jól használható a különböző geometriai adatokkal rendelkező, de közel azonos fókusztávolságú lencsék szimmetriájának ill. aszimmetriájának jellemzésére. „S” értéke a leképezési hibákat (aberrációkat) befolyásolja. | „S” egy-egy lencsetag jellemzője. Az összefüggés jól használható a különböző geometriai adatokkal rendelkező, de közel azonos fókusztávolságú lencsék szimmetriájának ill. aszimmetriájának jellemzésére. „S” értéke a leképezési hibákat (aberrációkat) befolyásolja. | ||
| − | * | + | *<u>Szóródási folt:</u> Ha a lencsére nagy átmérőjű, az optikai tengellyel párhuzamos fénynyalábot ejtünk, akkor az a paraxiális közelítéstől eltérően nem egy pontban egyesül. Egy, az optikai tengelyre merőleges sík (általában a képsík) és a rendszeren átvezetett fénysugarak metszéspontjainak halmazát szóródási foltnak nevezzük. Elég sok sugarat átvezetve a képsíkon a szóródási folt jól modellezi a fényintenzitás eloszlást. Ahol nagy a metszéspontok sűrűsége, ott az intenzitás is nagy. Kevés metszéspont kisebb intenzitást jelent. |
| − | * | + | *<u>Aberráció:</u> tágabb értelemben minden képalkotási hiba. Szűkebb értelemben a leképezés elmélet harmadrendű közelítésében megkülönböztethető leképezési hibák fajtái. Néhány fontosabb aberráció jellemző képfoltját mutatja a [[#fig:4a|11.4.ábra]]. |
| − | * | + | *<u>Diffrakciókorlátos rendszer:</u> A közel ideális, geometriai optikai hibáktól mentes rendszerek képfoltja sem matematikai értelemben vett pont, hanem egy kis tartomány. Ilyen esetekben a képfolt méretét a diffrakció (fényelhajlás) határozza meg (felülről korlátozza). Kör alakú lencsét feltételezve a képfolt sugarát paraxiális esetben (f >> A) a ([[#eq:15|11.15]]) összefüggés adja meg (lásd a [[#fig:5a|11.5.ábrát]]). |
| − | + | ||
| − | + | ||
| − | + | {{eq|\Delta r {{=}} \frac{1.22\lambda f}{A}|eq:15|(11.15)}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | , ahol $\Delta r$ a diffrakciós folt első nullahelyének sugara, „f” a lencse fókusztávolsága, „A” a fénynyaláb átmérője a lencsén, $\lambda $ a hullámhossz az adott közegben. Az optikai rendszert diffrakció korlátosnak hívjuk, ha a geometriai optikai úton számolt szóródási folt méret kisebb, mint a diffrakciós folt. | |
| − | + | *<u>Numerikus apertúra (NA):</u> Egy hengerszimmetrikus nyaláb konvergenciáját leíró számadat, amelynek értéke definíció szerint: | |
| − | , | + | |
| − | + | $$NA = n \cdot \sin \Theta$$,ahol „n” a közeg törésmutatója, $\Theta $ pedig a nyaláb fél-kúpszöge (lásd a [[#fig:5a|11.5.ábrát]]). Az NA-t lencsék vagy objektívek felbontóképességének jellemzésére szokták használni (NA nagy → felbontóképesség nagy), mivel nagyobb kúpszögek esetén a ([[#eq:15|11.15]]) összefüggés helyett a diffrakciós folt mérete az alábbi képlettel számolható ki: | |
| − | + | ||
| + | $$\Delta r = \frac{{1.22{\lambda _0}}}{{2 \cdot NA}}$$ | ||
| + | ,ahol $\lambda{}_{0 }$ a levegőben mért hullámhossz. | ||
| + | |||
| + | ====Néhány fontosabb aberráció jellemző képfoltja geometriai optikai közelítésben==== | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|Ideális leképzés.JPG|fig:4a|11.4.a ábra. Ideális leképezés}} | ||
| + | | {{fig|Defókusz.JPG|fig:4b|11.4.b ábra. Defókusz}} | ||
| + | | {{fig|Nyíláshiba.JPG|fig:c|11.4.c ábra. Nyíláshiba}} | ||
| + | |} | ||
| + | |||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|Kóma.JPG|fig:4d|11.4.d ábra Kóma}} | ||
| + | | {{fig|Asztigmatizmus.JPG|fig:4e|11.4.e ábra Asztigmatizmus}} | ||
| + | |} | ||
| + | |||
| + | ====Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések==== | ||
| + | A ([[#fig:5a|/b]]) és ([[#fig:5c|/c]]) ábrán a lencse fókuszpont környéki intenzitás eloszlása látható (Airy-folt), ideális leképezés esetén. | ||
| + | |||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
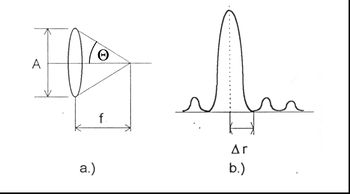
| + | | {{fig|Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések A és b.JPG|fig:5a|11.5.a-b ábra. Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések}} | ||
| + | | {{fig|Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések C.JPG|fig:5c|11.5.c ábra. Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések}} | ||
| + | |- | ||
| + | |} | ||
===Vastag lencsékre és paraxiális sugarakra vonatkozó közelítő összefüggések=== | ===Vastag lencsékre és paraxiális sugarakra vonatkozó közelítő összefüggések=== | ||
| + | {{eq|f {{=}} \frac{1}{\left (\left (n - 1\right )\left (\frac{1}{R_1} - \frac{1}{R_2} + \frac{n - 1}{n} \cdot \frac{t}{R_1 \cdot R_2}\right )\right )}|eq:16|(11.16)}} | ||
| + | {{eq|S_1 {{=}} \frac{R_1 \cdot t}{\left (n \cdot \left (R_1 - R_2\right ) -\left ( n - 1\right )t\right )}|eq:17|(11.17)}} | ||
| + | {{eq|S_2 {{=}} \frac{R_1 \cdot t}{\left (n \cdot \left (R_2 - R_1\right ) +\left ( n - 1\right )t\right )}|eq:18|(11.18)}} | ||
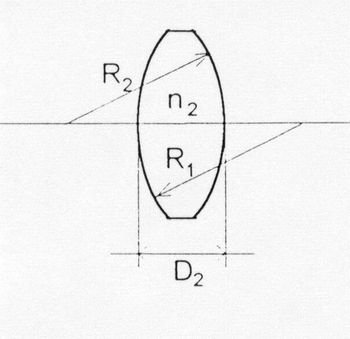
| + | ahol „f ” a lencse effektív fókusztávolsága, „n” a lencse törésmutatója, R<sub>1</sub> és R<sub>2</sub> a lencse első és második törőfelületének görbületi sugara, „t” avastagsága, valamint S<sub>1</sub> a tárgy-, S<sub>2</sub> a képoldali, azaz első és hátsó fősík helye a lencsefelületekhez képest (lásd a [[#fig:6|11.6 ábrát]]). | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|Vastag lencséknél alkalmazott jelölések.JPG|fig:6|Vastag lencséknél alkalmazott jelölések 11.6 ábra}} | ||
| + | |} | ||
| − | |||
| + | ===Az alkalmazott optikai tervező program leírása=== | ||
| + | A labormérés során az OSLO LT 6.1 szoftvert használjuk, amely az optikai modellezésben és ipari lencsetervezésben széles körben használt OSLO programcsalád legegyszerűbb változata. A program oktatásra/otthoni gyakorlásra ingyenesen letölthető a '''''http://www.lambdares.com/''''' honlapról. A program felhasználóbarát grafikus felülettel rendelkezik (ld. [[#fig:7|11.7. ábra]]), amely három különböző ablaktípust használ: | ||
| + | * Lencse adatokat tartalmazó és azok szerkesztésére szolgáló táblázat (egy ablak) | ||
| + | * Szöveges vagy numerikus kimenetek megjelenítésére szolgáló szöveges ablak (egyszerre kettő használható) | ||
| + | * Képi kimenetek megjelenítésére szolgáló grafikus ablak (egyszerre több is használható) | ||
| + | A program kezelése legegyszerűbben a menürendszeren keresztül vagy az ablakokon található ikonokkal történhet, de rendelkezik egy parancs-sorral, ahol közvetlen utasítások is kiadhatók. A szoftver alapszintű kezelését a mérési feladatok végrehajtása során fogjuk megtanulni, ennek megfelelően annak ismertetése is ott történik. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|Az OSLO LT 6.1 felhasználói felülete.JPG|fig:7|11.7.ábra Az OSLO LT 6.1 felhasználói felülete}} | ||
| + | |} | ||
==Mérési feladatok== | ==Mérési feladatok== | ||
| + | Végezze el az alábbi mérési feladatokat a számozás sorrendjében. Kérjük, hogy a használt lencsefájlokat ne változtassa meg és ne törölje le! A jegyzőkönyv készítéséhez használjon szövegszerkesztő programot. Az OSLO grafikus és szöveges ablakainak tartalmát jobb egérgombbal rákattintva a '''Copy to clipboard''' vagy a '''Copy page''' utasítással tudja másolni és a '''Szerkesztés beillesztés''' paranccsal a szövegszerkesztőbe illeszteni. Az adatok bevitelére használt ablakok bal felső sarkában található zöld pipával az ablakot a változtatásokat elmentve zárja be (OK), míg a piros X a változtatásokat nem veszi figyelembe (CANCEL). A szükséges grafikonok készítéséhez használjon táblázatkezelő programot! Minden egyes pontnál értelmezze / diszkutálja az eredményt! | ||
| + | '''1. feladat: A lencserendszer beolvasása''' | ||
| + | Indítsa el az OSLO LT programot a Start menü vagy az asztalon található ikon segítségével. A '''File''' menü '''Open lens''' parancsával nyissa meg a '''C:\Hallg mérés\singlet.len''' lencsefájlt. A '''Lens''' menü '''Lens drawing / System utasítással''' rajzoltassa ki a beolvasott lencsét (a felugró ablakban az eredeti beállítások megőrzéséhez válassza az OK gombot). Ugyanezt megteheti egyszerűbben a grafikus ablak tetején levő lencserendszert ábrázoló ikonra kattintva. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|A „singlet” lencse rendszerrajza.1.JPG|fig:8|11.8. A „singlet” lencse rendszerrajza}} | ||
| + | |} | ||
| − | == | + | Ekkor a [[#fig:8|11.8. ábrán]] bemutatott kép jelenik meg, amely fejlécében mutatja a lencse elnevezését, effektív fókusztávolságát (ld. [[#fig:6|11.6. ábra]]) és a képoldali (jobb oldal) nyaláb numerikus apertúráját. Látható, hogy a rendszer egy szimmetrikus bi-konvex lencsét tartalmaz, előtte egy külön apertúra helyezkedik el. A lencsét a végtelenből jövő párhuzamos sugárnyalábok világítják meg. A nyalábok rendre 0<sup>o</sup>, 6<sup>o</sup> és 12°-os szöget zárnak be az optikai tengellyel (z-tengely). A maximális nyalábszöget (tárgyszög) a lencse szerkesztő ablak '''field angle''' cellájában tudjuk átállítani (lásd a [[#fig:9|11.9.ábrát]]), a nyalábok száma, szöge és a megjelenített sugarak száma pedig a '''Lens''' menü '''Lens drawing conditions''' pontjában állítható (lásd a [[#fig:10|11.10.ábrát]]). |
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|A tárgyszög beállítása.JPG|fig:9|11.9. A tárgyszög beállítása}} | ||
| + | | {{fig|A lencserajzolás paramétereinek beállítása.JPG|fig:10|11.10. A lencserajzolás paramétereinek beállítása}} | ||
| + | |} | ||
| − | *[[Media:LENCSEHIBÁK.pdf|Lencsehibák vizsgálata sugárkövetés módszerével]] | + | {| cellpadding="5" cellspacing="0" align="center" |
| + | |- | ||
| + | | {{fig|A singlet.len lencse geometriai adatai.JPG|fig:11|11.11. A singlet.len lencse geometriai adatai}} | ||
| + | |} | ||
| + | * R<sub>1</sub> = 10mm (C<sub>1</sub> = 1/R<sub>1</sub> = 0.1) | ||
| + | * R<sub>2</sub> = -10mm (C<sub>2</sub> = 1/R<sub>2</sub> = -0.1) | ||
| + | * D<sub>1</sub> = 2mm | ||
| + | * apertúra sugár = 3 mm | ||
| + | * anyag: Schott BK7 üveg | ||
| + | |||
| + | '''2. feladat: A beolvasott adatok ellenőrzése''' | ||
| + | |||
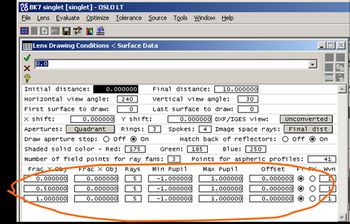
| + | A '''Lens''' menü '''Show Surface Data / All data''' utasításával listázza ki a lencseadatokat a képernyőre. Hasonlítsa össze azt [[#fig:12|11.12.ábrán]] bemutatott adatokkal. Az első szakasz a lencse geometriai adatait tartalmazza (görbületi sugár, vastagság, apertúra sugár, anyag) minden egyes felületre. A program a vastagság és anyag tulajdonságot az adott anyagot megelőző felület tulajdonságaihoz rendeli hozzá. Így az első sor (a program számozása szerint 0. jelölése OBJ) a tárgysíkot írja le, amelynek 10<sup>20</sup> mm-es vastagsága azt jelenti, hogy a tárgy a végtelenben van, azaz a lencsét párhuzamos fénysugarak világítják meg. A második sor, a program számozása szerint 1. felület, a lencse első felülete. A harmadik sor (a program számozása szerint 2) a lencse hátsó felülete és végül a negyedik a képsík. A második szakasz a különböző felületeken érvényes apertúra sugarakat (lencseátmérő fele) mutatja, harmadik a használt hullámhosszakat és azok súlyfaktorát, amellyel az adott hullámhossz az foltméret számításnál szerepel. Az utolsó két szakaszban leírja a használt üvegek törésmutatóját és áteresztését (transzmisszió) a fent definiált hullámhosszakra. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|Lencsehiba_12.png|fig:12|11.12. A singlet.len fájlban található lencse adatai a program által kilistázva}} | ||
| + | |} | ||
| + | |||
| + | '''3. feladat: Szóródási foltok kirajzolása''' | ||
| + | |||
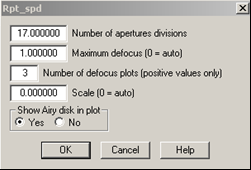
| + | A szóródási foltokat először egyetlen hullámhosszon vizsgáljuk. Ezért a lencse-adatokat szerkesztő ablakban kattintson a '''wavelengths''' gombra és ott törölje ki a 2. és 3. hullámhosszt, így csak egyetlen hullámhossz marad (587,56 nm). A '''Window''' menü '''Graphics/New''' parancsával nyisson új grafikus ablakot, majd az '''Evaluate''' menü '''Spot diagram/Report graphic''' utasításával rajzolja ki a lencse szóródási foltjait. A felugró ablakban adja meg az ábrázolt sugarak számát (aperture divisions), a képsíktól való maximális z irányú eltérést (max. defocus) és az ábrázolandó defókusz értékek számát a [[#fig:13a|11.13.a ábrának]] megfelelően. Ekkor a [[#fig:13a|11.13.b ábrán]] látható kép jelenik meg. Az egymás alatti három ábrasorozat rendre az optikai tengellyel 12°, 8,46° és 0°-os szöget bezáró nyalábokhoz tartozik. (Az értékeket a program az egyes sorok előtt az ábra bal oldalán tünteti fel). Egy vízszintes ábrasoron belül a középső szóródási foltot pontosan a képsíkban, az előtte illetve utána lévő két másik foltot a képsíkkal párhuzamos, de kismértékben eltolt síkokban kapjuk. Az eltolás mértéke (defókusz) a függőleges oszlopok alatt látható. Lehetőség van arra is, hogy a középső oszlopot is kitoljuk a képsíkból. Ekkor a lencse-adatokat szerkesztő ablakban az utolsó lencsefelülethez tartozó vastagság értékét kell átállítani. | ||
| + | |||
| + | Az ábra bal alsó részén egy függőleges vonal, és egy mellé írt szám mutatja a méretskálát (mm-ben) a képsíkban. Ez lehetővé teszi, hogy durván meghatározzuk a szóródási foltok méretét. Az ábra alapján hol van az optimális fókusz? Miért? | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|Lencsehibak_13a.png|fig:13a|11.13.a. Paraméterek a szóródási folt rajzolásához a.) A rendszer szóródási foltjai}} | ||
| + | | {{fig|Lencsehibak_13b.png|fig:13b|11.13.b. Paraméterek a szóródási folt rajzolásához b.) három különböző irányú síkhullám megvilágítás esetén, a paraxiális fókuszsíkban és azzal párhuzamos, attól a Z tengely mentén 0.5 és 1 mm-re eltolt síkokban}} | ||
| + | |} | ||
| + | |||
| + | '''4. feladat: A szóródási folt vizsgálata a képsík helyzetének függvényében''' | ||
| + | |||
| + | A szóródási foltok segítségével az optikai tengellyel párhuzamos sugárnyaláb esetén rajzolja fel a szóródási folt méret - képsík defókusz görbét a ±2-mm tartományban. A görbe pontjait pl. a kinyomtatott diagramokról mérheti le. A jobb felbontás és nagyobb pontosság érdekében érdemes megnövelni az ábrázolandó defókusz (képsík eltolás) értékek és sugarak számát, valamint átállítani az ábrázolás léptékét (Scale). Kísérletezze ki a legjobb beállításokat és vegye fel a görbét. Ábrázolja a kapott eredményt! | ||
| + | |||
| + | A foltméretek pontos és gyors meghatározásához igénybe veheti a program által nyújtott automatikus számolásokat is. A fókuszfolt méretét kiszámoltathatja az '''Evaluate''' menü '''Spot diagram/Spot size analysis''' pontjában (object point 0,0,0, best focus: NO!). Az itt kapott foltsugár (GEO RMS R) az átvezetett sugaraknak a képsíkkal vett metszéspontjaiból 2D átlagot számol és meghatározza az attól való eltérés négyzetes középértékét (súlypont). Ez az ún. RMS foltméret használatos a geometriai optikai felbontás jellemzésére. | ||
| + | |||
| + | A szóródási foltméret - képsík defókusz görbe kvalitatív vizsgálatára alkalmas a lencse rendszerrajza is, ha csak az optikai tengellyel párhuzamos nyalábot ábrázoljuk nagyobb számú átvezetett sugárral (ld. '''Lens drawing conditions''' és [[#fig:10|11.10.ábra]]). Rajzoltassa ki a sugarakat és a fókuszpontra zoomolva figyelje meg a fénynyaláb burkoló görbéjét (zoomolás: kijelölheti a területet a bal egérgombot lenyomva tartott egeret elhúzva). Hasonlítsa össze a foltméretekből kapott görbe és az ábra jellegét! | ||
| + | |||
| + | '''5. feladat: Paraxiális fókuszpont meghatározása''' | ||
| + | |||
| + | A program segítségével határozza meg a lencse paraxiális fókuszpontjának a távolságát, az utolsó lencsefelülettől mérve! A kapott eredményt hasonlítsa össze a vastag lencsékre és tengelymenti sugarakra érvényes közelítő formulából számított értékkel! ([[#eq:16|11.16]] összefüggés). A fókuszpont helyét úgy határozzuk meg, hogy elindítunk egy, a tengellyel párhuzamos, a tengelyhez nagyon közeli sugarat és meghatározzuk a tengellyel való metszését. A sugarat az '''Evaluate''' menü '''Single ray trace''' parancsával indíthatjuk. A paramétereket a következőképpen állítsuk be: | ||
| + | |||
| + | '' | ||
| + | output format: full, | ||
| + | surface selection: all, | ||
| + | FY=0.01, | ||
| + | set object point 0,0,0'' | ||
| + | |||
| + | Ilyen módon az optikai tengellyel párhuzamos, attól (0.01 $ \times$ apertúra =) 0.03 mm-re haladó sugarat indítunk, és annak átvezetését a szöveges ablakban követhetjük nyomon. A szöveges ablakban megjelenő táblázat első oszlopa tartalmazza felületenként az optikai tengelytől mért távolságot (Y) és alatta az iránykoszinuszok értékeit (L). Rajzolja meg vázlatosan a sugár útját a képsík közelében és elemi geometriai módon határozza meg a tengellyel való metszéspontot. Állítsa be a képsík „vastagság” értékét úgy, hogy a képsík az így meghatározott helyre kerüljön. Próbáljon ki más, a tengelytől kicsit távolabbi sugarakat is. Figyelje meg a különbséget. | ||
| + | |||
| + | '''6. feladat: Nyíláshiba (szférikus aberráció, gömbi eltérés) vizsgálata''' | ||
| + | |||
| + | A nyíláshiba jól jellemezhető a paraxiális fókuszban mérhető nyalábátmérővel A nyalábátmérő azonos fókusztávolság és azonos lencsevastagság esetén függ a lencse görbületi sugaraitól. Határozza meg és ábrázolja a [[#eq:91|11.1 táblázatban]] megadott lencsék paraxiális nyalábátmérőjét a lencsék ún. alaktényezője függvényében! A lencséket 4 mm átmérőjű, a z- tengellyel párhuzamos sugárnyalábbal világítjuk meg. A lencsék vastagsága D=2mm, törésmutatója n=1,51418 azonos. Közelítőleg azonos a fókusztávolságuk is. A szóródási foltok fölrajzoltatásával határozza meg, hogy az alaktényező mely értéknél lesz minimális a nyalábátmérő! Szükség lehet az aberrációs skála, a defókusz vagy a "Z" irányú lépésköz optimális beállítására. | ||
| + | |||
| + | A lencse adatokat szerkesztő ablakban cserélje ki a törőfelületek görbületi sugarát! Az előzőek szerint határozza meg a minimális nyalábátmérőt a táblázatban szereplő összes lencsére! A nyalábátmérő meghatározásához igénybe veheti a program által nyújtott automatikus számolásokat. A paraxiális fókusz pontos beállításához (a konfiguráció minden megváltoztatása után!) kattintson a képsík vastagságértéke mellett jobbra található téglalapra és válassza az '''Autofocus – paraxial focus''' utasítást. A fókuszfolt méretét ezentúl pontosan kiszámoltathatja az '''Evaluate''' menü '''Spot diagram/Spot size analysis''' pontjában (object point 0,0,0, best focus: NO!). Az itt kapott foltsugár (GEO RMS R) az átvezetett sugarak a képsíkkal való metszéspontjaiból 2D átlagot számol (folt súlypontja) és meghatározza az attól való eltérés négyzetes középértékét. Ez az ún. RMS foltméret használatos a geometriai optikai felbontás jellemzésére. Az előzőektől különböző foltméretet kap, ha az az '''Autofocus – paraxial focus''' helyett az az '''Autofocus – Minimum RMS spotsize-On axis (monochromatic)''' beállítást választja. Magyarázza a különbséget! | ||
| + | |||
| + | Ábrázolja a foltméretet az alaktényező függvényében a paraxiális és a legkisebb foltméretet adó valós fókuszpontban is! Minden lencseátmérő 6 mm legyen! | ||
| + | |||
| + | $$ | ||
| + | \begin{array}{|c|c|c|} | ||
| + | \hline | ||
| + | {\bf R_1(mm)} & {\bf R_2 (mm)} & {\bf S} \\ | ||
| + | \hline | ||
| + | inf & -5.00 & -1.00 \\ | ||
| + | \hline | ||
| + | 10 & -10 & -0.00 \\ | ||
| + | \hline | ||
| + | 5.0 & inf & 1 \\ | ||
| + | \hline | ||
| + | 3.33 & 10 & 2 \\ | ||
| + | \hline | ||
| + | \end{array} | ||
| + | $$ | ||
| + | {{eq|11.1.\ t\acute{a}bl\acute{a}zat.\ Lencseadatok\ a\ 6.\ feladathoz|eq:91|(11.1.)}} | ||
| + | |||
| + | Hasonlítsa össze a fenti foltméreteket az előzőeknek megfelelő fókusztávolságú és apertúrájú belépő oldalán aszférikus felülettel határolt fókuszáló lencse '''(C:\Hallg mérés\singlet_asphere.len)''' által adott szóródási folttal. A példa mutatja, hogy egy aszférikus felülettel a gömbi eltérés igen jól korrigálható. | ||
| + | |||
| + | '''7. feladat: A kóma hiba tanulmányozása''' | ||
| + | |||
| + | Növelje meg a tárgyszöget ('''Field angle''') 20°-ra és a 3. feladathoz hasonlóan rajzolja fel ismét a szóródási foltokat. Az ábra szemléletesen mutatja az úgynevezett kómát (üstökös hibát). A sugarak és az optikai tengely által bezárt szög növelésével a képsíkon egy jellegzetes üstökös szerű képet kapunk. A képnek van egy erősen megvilágított középső foltja („az üstökös magja”). Ezt a lencserendszerbe belépő nyaláb középső tartományán áthaladó fénysugarak alakítják ki. A belépő nyaláb szélén haladó sugarak egy sokkal kisebb intenzitású, de a mag méreténél kétszer háromszor nagyobb területre szóródnak szét. A tárgyszög növelésével a mag középpontja és a farokrész eltolódik. | ||
| + | |||
| + | A belépő nyalábban koncentrikus körökben elhelyezkedő sugarak átvezetésével még szemléletesebb képet kapunk ('''Evaluate''' menü '''Spot diagram– Recipolar spot diagram'''). Egy sajnálatos programhiba miatt ezen utasítás nem engedi a képszög állítását, így a 20 fokos tárgyszögre akkor kapja a megfelelő ábrát, ha előtte pl. '''Spot diagram– single spot diagram''' utasítást hajt végre és ott beállítja a kívánt relatív képszöget ('''set object point''', FBY=1) A tengellyel párhuzamos sugarak esetén jól láthatók a körök, amelyek a szög növelésével már eltorzulnak és nem koncentrikusak, az egyre nagyabb sugarú körökből érkező fénysugarak egyre jobban eltolódnak a kisebb sugarú körökből származó fénysugarakhoz képest. Rajzoltassa ki az így kapott szóródási foltot! | ||
| + | |||
| + | '''8. feladat: Színi hiba vizsgálata''' | ||
| + | |||
| + | Olvassa be újra a singlet.len fájlt (kilépésnél <u>NE mentse el a lencsefájl változásait</u>!). A lencse úgynevezett BK7-s üvegből készült. A lencsét 6 mm átmérőjű fehér színű sugárnyalábbal világítjuk meg. Az üveg törésmutatóját a hullámhossz függvényében a [[#eq:92|11.2 táblázatban]] adtuk meg. Az előzőekben sárga fényben meghatároztuk a fókuszpont helyét. Becsülje meg a folt növekedését, ha mindhárom hullámhosszt figyelembe vesszük. | ||
| + | |||
| + | Rajzoltassa ki a szóródási foltokat három színre. Hasonlítsa össze a 3. feladatban kapott eredményekkel | ||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | ! Szín | ||
| + | ! Hullámhossz (μm) | ||
| + | ! Törésmutató | ||
| + | |||
| + | |- | ||
| + | | align="center" | vörös | ||
| + | | align="center" | 0.65628 | ||
| + | | align="center" | 1.51418 | ||
| + | |- | ||
| + | | align="center" | sárga | ||
| + | | align="center" | 0.58959 | ||
| + | | align="center" | 1.51666 | ||
| + | |- | ||
| + | | align="center" | kék | ||
| + | | align="center" | 0.48613 | ||
| + | | align="center" | 1.52225 | ||
| + | |} | ||
| + | {{eq|11.2.\ t\acute{a}bl\acute{a}zat.\ Korona\ddot{u}veg\ t\ddot{o}r\acute{e}smutat\acute{o}ja\ k\ddot{u}l\ddot{o}nb\ddot{o}z\ddot{o}\ hull\acute{a}mhosszakra|eq:92|(11.2.)}} | ||
| + | |||
| + | '''9. feladat: Diffrakciós korlát vizsgálata''' | ||
| + | |||
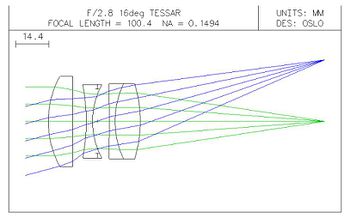
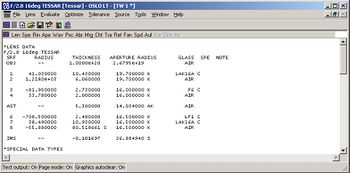
| + | Olvassa be a '''tessar.len''' fájlt, mely a [[#fig:15|11.15. ábrán]] látható adatokkal jellemzett lencsét tartalmazza. A rendszer rajzát a [[#fig:14|11.14. ábrán]] mutatjuk be. A lencseadatok kilistázásával ellenőrizze a paramétereket. | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | {{fig|A tessar.len fájlban tárolt lencse, és az átvezetett fénysugarak.1.JPG|fig:14|11.14. A tessar.len fájlban tárolt lencse, és az átvezetett fénysugarak}} | ||
| + | | {{fig|A tessar.len fájlban tárolt lencse adatai.JPG|fig:15|11.15. A tessar.len fájlban tárolt lencse adatai}} | ||
| + | |} | ||
| + | |||
| + | A lencsehibák abból adódnak hogy gömbfelületekkel nem lehet ideális hibamentes leképezést megvalósítani. Ez azt jelenti, hogy egy geometriai pont képe nem pont, hanem a lencse paramétereitől függő kisebb vagy nagyobb tartomány. A hiba jelentősen csökkenthető ha bonyolult optimalizációs eljárás eredményeképpen több gömbfelületből álló lencserendszert alkalmazunk. A '''tessar.len''' fájlból beolvasott négytagú rendszer is ilyen. Ezek a rendszerek azonban csak az optimalizálásnál figyelembe vett tárgyszögnél kisebb szögekre, és az optimalizálásnál használt belépő nyaláb méret esetén működnek megfelelően. Ettől kismértékben eltérve a rendszer tulajdonságai rohamosan romlanak. | ||
| + | |||
| + | A geometriai optikai hibák és a képfolt mérete jelentősen csökkenthető a belépő nyaláb méretének csökkentésével. Az alábbiakban megvizsgáljuk, hogy meddig kell csökkenteni az előzőekben vázolt optimalizált lencserendszer apertúráját ahhoz, hogy a rendszer a tengellyel párhuzamos nyalábra diffrakciókorlátos legyen. | ||
| + | |||
| + | A belépő nyaláb méretét a lencse szerkesztő ablak '''Ent beam radius''' pontja alatt változtathatjuk meg. A fájlból beolvasott rendszer belépő nyaláb sugara 15 mm. Csökkentse ezt addig, míg a fókuszpontban a szóródási folt mérete a ([[#eq:15|11.15]]) összefüggéssel megadott diffrakciós korlát alá süllyed. A belépő nyaláb méret módosításával változik a diffrakciós foltméret is. Ezért ezt minden módosítás után újra kell számolni. Ábrázolja az RMS foltméretet és a diffrakciós foltméretet a belépő nyaláb sugarának függvényében tengellyel párhuzamos nyalábokra. Határozza meg azokat a belépő nyaláb méreteket, amely mellett a rendszer diffrakció-korlátos. | ||
| + | |||
| + | A valódi, kísérletileg mérhető intenzitáseloszlást természetesen a geometriai és a diffrakciós effektusok együttes figyelembevételével lehet megkapni. Ezt a program úgy számolja ki, hogy a geometriai hibák által eltorzított és a rendszer apertúrája által levágott hullámfrontot Fourier transzformálja és azt négyzetre emeli. Az így kapott intenzitáseloszlást pontszórásfüggvénynek nevezzük (Point spread function: PSF). | ||
| + | |||
| + | Vizsgálja meg a pontszórásfüggvényt legalább három apertúra értékre: a teljes apertúrára, az előző pontban megállapított diffrakciós határra, és egy annál lényegesen kisebb apertúrára. A programban ezt az '''Evaluate''' menü '''Spread Function – Plot PSF map''' paranccsal teheti meg. Melyik esetben nevezné a rendszer felbontását a legnagyobbnak? Miért? | ||
| + | |||
| + | '''10. feladat: Képmező hajlás tanulmányozása''' | ||
| + | |||
| + | Az előző pontban vizsgált lencserendszernél állítsa be a belépő nyaláb sugarát 15 mm-re, és töröljön ki 2 hullámhosszat, hogy monokromatikus esetben vizsgálhassa a rendszert. Rajzoltassa ki a szóródási foltokat 3. pontban leírtakhoz hasonlóan. Állítsa be úgy a maximális defókuszt és a „Z” irányú lépésközt, hogy mind a három tárgyszögre egyszerre legyen látható a legkisebb képfolt. A képmező elhajlást a 0°-os és a 15°-os irányokhoz tartozó minimális foltok „Z”- irányú távolságával jellemezhetjük. Határozza meg ezt az értéket! | ||
| + | |||
| + | ==PDF formátum== | ||
| + | *[[Media:LENCSEHIBÁK.pdf|Lencsehibák vizsgálata sugárkövetés módszerével (nem korrigált változat)]] | ||
</wlatex> | </wlatex> | ||
| + | |||
| + | <!--Utolso szerkesztes: 2013.09.25--> | ||
A lap jelenlegi, 2013. szeptember 25., 15:16-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Bevezetés
A személyi számítógépek tömeges elterjedése sok más klasszikus tudományterület mellett a fizika, ezen belül a geometriai optika módszereit is gyökeresen megváltoztatta. A zárt formulák és képletek helyett széles körben elterjedtek a numerikus módszerek. Számítógépek alkalmazásával kiküszöbölhető a geometriai optikával együtt járó algebrai számítások nagy része, és a számítási eredmények szemléletesen meg is jeleníthetők a képernyőn. Interaktív programok alkalmazásával lehetőség van számítógépes kísérleteket végezni és összetett lencserendszereket tervezni, optimalizálni.
Jelen mérés is egy ilyen grafikus, interaktív, számítógépes kísérletezésre alkalmas programra mutat példát, amely az áthaladó fénysugarak valós (nem csak az elsőrendben közelített, ú.n. paraxiális) menetét határozza meg. A mérésben használt program egy lencsetervező rendszer, amely alkalmas az optikai rendszerek részletes analízisére, és optimalizálására. A mérés során a program nyújtotta szolgáltatások közül csak a sugárátvezetést és a grafikus megjelenítést használjuk ki. Az optikai rendszerek részletes analízise, és az optimalizálás messze meghaladja egy alap fizika laboratórium kereteit (ezt az Optikai rendszerek tervezése c. választható tárgy keretei között sajátíthatják el).
A geometriai optika középiskolából ismert egyszerű közelítő eljárásai (ld. pl. lencsetörvény) csak az optikai tengelyhez közeli tárgy-kép pontokra, és a tengellyel kis szöget bezáró paraxiálisnak nevezett sugarakra érvényesek (lásd pl. Budó-Mátrai: Kísérleti Fizika III. 35-76. oldal). A paraxiális közelítés hatalmas előnye abban rejlik, hogy keretei között teljesülnek az ideális képalkotást feltételei (többek között éles, torzításmentes az így kapott kép). A tengelytől távol haladó, valamint a tengellyel nagy szöget bezáró sugarak különböző képalkotási hibákat okoznak, mint pl. nyíláshiba (vagy gömbi eltérés), asztigmatizmus, kóma, képmezőhajlás. A lencsék anyagaként használt üvegek törésmutatójának hullámhossz függése (diszperziója) miatt fellép továbbá színi hiba (kromatikus aberráció) is. A felsorolt hibák pontos tárgyalása bonyolult és hosszadalmas. Jelen mérés célja ezen hibák kísérleti bemutatása a számítógép adta lehetőségek felhasználásával. (A hibák leírását lásd Budó-Mátrai: Kísérleti Fizika III. 65-69 oldal).
A sugárkövetés fizikai alapjai
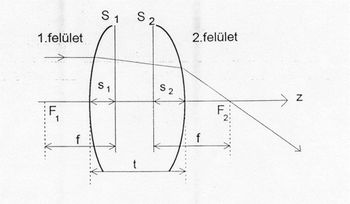
A sugárkövetés során a törési törvény sorozatos alkalmazására kerül sor. A számításokat a 11.1.ábra koordináta rendszerében végezzük. Gömbsüveg alakú lencsék, tükrök esetén az egyes törő-/ tükröző felületeket négy adattal jellemezzük:
- - görbületi sugár (görbület ≡ 1 / görbületi sugár),
- - a törőfelületet követő anyag törésmutatója,
- - a törőfelületet követő felület távolsága,
- - a törőfelület apertúrájának (nyílásának) sugara
(Ezt a számításnál általában nem használja a program, csak a rajz elkészítésénél).
Az abszolút koordináta-rendszer origója a tárgy és az optikai tengely metszéspontjában van. A z-tengely egybeesik az optikai tengellyel. Az első törőfelület előtt a program automatikusan levegőt (n0=1 törésmutatót) tételez fel. Az utolsó törőfelület után - a felhasználó által megadott távolságban - a program automatikusan egy zérus görbületű felületet (sík ernyőt) tételez fel (képsík).
Egy fénysugarat a tér adott pontjában általános esetben hat adat ír le:
- X0 : x koordináta,
- Y0 : y koordináta,
- Z0 : z koordináta,
- K : az x tengellyel bezárt szög koszinusza,
- L : az y tengellyel bezárt szög koszinusza,
- M : a z tengellyel bezárt szög koszinusza.
Az (X0, V0, Z0), a sugár kiinduló pontját, vagy egy törőfelülettel alkotott metszéspontját jelenti. (K, L, M) jelöli az iránykoszinuszokat (azaz a fénysugár irányú egységvektor koordinátáit), amelyek közül csak kettő független. A számítások során a program meghatározza a sugár metszéspontját a következő törőfelülettel, és a törési törvény alapján kiszámítja a sugár új irányát/iránykoszinuszait a következő közegben. A metszéspont meghatározása a (11.1) egyenletrendszer megoldását jelenti:
![\[x = {{\rm{X}}_{\rm{0}}} + {\rm{K}}t\]](/images/math/4/5/e/45ece3cbd11a9e89dd02e8148658dd24.png)
![\[y = {{\rm{Y}}_{\rm{0}}} + {\rm{L}}t\]](/images/math/5/b/b/5bb3d96169c5569d5cc7ed90275b8716.png)
![\[z = {{\rm{Z}}_{\rm{0}}} + {\rm{M}}t\]](/images/math/b/c/1/bc14fe8287fd819bc8bf1ec6162a7ecf.png)
![\[{{R^2} = {x^2} + {y^2} + {(z - R)^2}}\]](/images/math/9/6/0/960de4162c3fc61eeea705653eb8af10.png)
A program a számításokat mindig egy lokális, az adott törőfelület és a z-tengely metszéspontjához rögzített koordináta-rendszerben végzi. Így a z koordináta értékeket ahol szükséges, át kell számolni abszolút koordinátákra. Az új közegben érvényes iránykoszinuszokat a 11.2.ábra alapján határozhatjuk meg. A számítások során a (11.2), (11.3) egyenletekből indulunk ki.
A beesési szög koszinusza a beeső nyaláb és a beesési pontba húzott felületi normális skaláris szorzatából számolható:
![\[C_xK + C_yL + C_zM = cos\alpha \]](/images/math/0/7/5/075f68ea98cdc048178f17187af2ccbe.png)
Itt (Cx, Cy, Cz) a beesési pontba húzott felületnormális vektor iránykoszinuszait jelentik (lásd a 11.2.ábrát). Az (Cx, Cy, Cz) iránykoszinuszok a beesési pont meghatározása után számolhatók. A törési szög a Snellius-Descartes-törvényből számolható:
![\[\frac{\sin \alpha }{\sin \beta }=\frac{n_1}{n_0}=\sqrt {\frac{{1 - {\cos ^2}\alpha }}{{1 - {\cos ^2}\beta }}}\]](/images/math/b/c/0/bc0439efa14b0f05d39a8abd109dbf3d.png)
Ebből az iránykoszinuszokra az alábbi egyenletet kapjuk:
![\[\frac{{1 - {\cos ^2}\alpha }}{{1 - {\cos ^2}\beta }} =\frac{n_1^2}{n_0^2}\]](/images/math/f/d/0/fd091cd2cfa3343b7987064cf266b2c1.png)
![\[{(1 - {\cos ^2}\alpha )}\cdot \frac{n_0^2}{n_1^2} = 1 - {\cos ^2}\beta \]](/images/math/0/9/7/097ba67763248d6863df256720f4a1ae.png)
Kifejezve 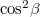 -t az alábbi egyenlet adódik:
-t az alábbi egyenlet adódik:
![\[{\cos ^2}\beta = 1 + ( {\cos ^2}\alpha - 1 )\cdot \frac{n_0^2}{n_1^2}\]](/images/math/e/3/d/e3d513c560263495fd7fe162441332a7.png)
Kihasználjuk továbbá azt a tényt, hogy a beeső nyaláb, a megtört nyaláb és a beesési merőleges egy síkban fekszik, így a megtört nyaláb irányába mutató egységvektor felírható a beeső nyaláb s0, és a beesési merőleges s2 egységvektorok lineáris kombinációjaként (lásd 11.3.ábra).
![\[\underline s_1 = k{\underline s_0} + u{\underline s_2}\]](/images/math/6/4/9/649c2dd3c471cd193bffe9aa9efd4ed4.png)
A (11.7) egyenletet s0 -al, illetve s2 -vel beszorozva az alábbi két egyenletet nyerjük:
![\[{\underline s _0}{\underline s _1} = \cos \left( {\alpha - \beta } \right) = k + u\cos \alpha\]](/images/math/d/b/3/db332be3c266e3547f08ffb80b3afd92.png)
![\[\underline s _2\underline s _1 = \cos \beta = k\cos \alpha + u\]](/images/math/7/7/1/77184125718371677ca472e96a5b9d47.png)
A (11.8) és (11.9) egyenletekből a „k” és „u” ismeretlen paraméterek meghatározhatók:
![\[k=\frac{\sin \beta }{\sin \alpha }=\frac{n_0}{n_1}\]](/images/math/e/a/c/eacead7a6fc144489b07b55453b1d2d1.png)
![\[{{u = \cos \beta - k \cdot \cos \alpha = \cos \beta \frac{{{{\rm{n}}_0}}}{{{{\rm{n}}_1}}} \cdot \cos \alpha}}\]](/images/math/7/b/9/7b9d66b166dc95213f0fa2161d5a2f80.png)
Ezek alapján a keresett egységvektor a következő egyenlet szerint írható le:
![\[\underline s _1 = k \cdot \underline s _0 + u \cdot \underline s _2 = \frac{n_0}{n_1} \underline s _0 + \frac{1}{n_1} \left(n_1 \cdot \cos \beta - n_0 \cdot \cos \alpha \right){\underline s _2}\]](/images/math/3/5/5/355c70f1865e32300353b36c622c2d5e.png)
A (11.12) vektoregyenlet három skalár egyenlet megoldását jelenti. Ezek megadják a megtört sugár (K', L', M') iránykoszinuszait.
![\[{\underline s _1} = \left[ {\begin{array}{*{20}{c}} {K'}\\ {L'}\\ {M'} \end{array}} \right]\]](/images/math/6/8/a/68a04787495db1efa5632dc7fdcb9b7c.png)
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
Ezek alapján a sugármenet számítására alkalmas program az alábbi számításokat végzi:
- - A belépő sugár (X0, Y0, Z0) kiinduló koordinátái és (K, L, M) iránykoszinuszai alapján a (11.1) egyenletrendszer megoldásával meghatározza a sugár és a felület (x, y, z) metszéspontját.
- - A (11.10), (11.11), (11.12) és (11.13) egyenletek alapján pedig kiszámítja a megtört sugár új iránykoszinuszait.
A program a fenti két számítási lépést végzi el az összes belépő sugárra és az összes törőfelületre. Az eredmények numerikusan listázhatók, vagy különböző grafikus formákban megjeleníthetők.
Néhány szokásos elnevezés, definíció
- Paraxiális sugarak: az optikai tengellyel kis szöget bezáró (kb. 5° vagy kisebb, amelyekre teljesül
![\setbox0\hbox{$sin\alpha \approx \alpha [rad]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/a/0/5/a05da770e401b3f6fb7b8c416d3cd3cf.png) ), és a tengelyhez közel haladó sugarak (x, y << R).
), és a tengelyhez közel haladó sugarak (x, y << R).
- Paraxiális fókuszpont: az optikai rendszer fókuszpontja végtelen távoli tárgypontból érkező paraxiális sugarak esetén.
- Fősík: paraxiális közelítésben az a két sík, amelyek m = +1-es nagyítású képei egymásnak. Ezek vékony lencse esetén egy síkká fajulnak, ami megegyezik a lencse síkjával. Tetszőlegesen bonyolult leképező rendszernél is meghatározható, és mindig csak kettő van belőle (első és hátsó).
- Effektív fókusztávolság: a paraxiális fókuszpont és a hátsó fősík „f” távolsága. Ha a „t” tárgytávolságot az első, a „k” képtávolságot pedig a hátsó fősíktól mérjük, akkor minden leképező rendszernél igaz a jól ismert lencsetörvény:
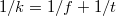 .
.
- Apertúra: magyarul nyílás. Ez lehet a lencse külső pereme, a lencsét tartó foglalat pereme, vagy egy külön erre a célra odahelyezett blende nyílása.
- Tárgyszög: a tárgytér szélén lévő tárgypontból az optikai rendszerhez érkező fénynyaláb központi fénysugarának az optikai tengellyel bezárt szöge.
- Alaktényező:
![\[S = \frac{R_1 + R_2}{R_1 - R_2}\]](/images/math/e/3/e/e3edeb88b4e7431df6877e1130263ade.png)
„S” egy-egy lencsetag jellemzője. Az összefüggés jól használható a különböző geometriai adatokkal rendelkező, de közel azonos fókusztávolságú lencsék szimmetriájának ill. aszimmetriájának jellemzésére. „S” értéke a leképezési hibákat (aberrációkat) befolyásolja.
- Szóródási folt: Ha a lencsére nagy átmérőjű, az optikai tengellyel párhuzamos fénynyalábot ejtünk, akkor az a paraxiális közelítéstől eltérően nem egy pontban egyesül. Egy, az optikai tengelyre merőleges sík (általában a képsík) és a rendszeren átvezetett fénysugarak metszéspontjainak halmazát szóródási foltnak nevezzük. Elég sok sugarat átvezetve a képsíkon a szóródási folt jól modellezi a fényintenzitás eloszlást. Ahol nagy a metszéspontok sűrűsége, ott az intenzitás is nagy. Kevés metszéspont kisebb intenzitást jelent.
- Aberráció: tágabb értelemben minden képalkotási hiba. Szűkebb értelemben a leképezés elmélet harmadrendű közelítésében megkülönböztethető leképezési hibák fajtái. Néhány fontosabb aberráció jellemző képfoltját mutatja a 11.4.ábra.
- Diffrakciókorlátos rendszer: A közel ideális, geometriai optikai hibáktól mentes rendszerek képfoltja sem matematikai értelemben vett pont, hanem egy kis tartomány. Ilyen esetekben a képfolt méretét a diffrakció (fényelhajlás) határozza meg (felülről korlátozza). Kör alakú lencsét feltételezve a képfolt sugarát paraxiális esetben (f >> A) a (11.15) összefüggés adja meg (lásd a 11.5.ábrát).
![\[\Delta r = \frac{1.22\lambda f}{A}\]](/images/math/3/8/9/38928a8bf5b3b2da41dce15a317ec32a.png)
, ahol 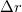 a diffrakciós folt első nullahelyének sugara, „f” a lencse fókusztávolsága, „A” a fénynyaláb átmérője a lencsén,
a diffrakciós folt első nullahelyének sugara, „f” a lencse fókusztávolsága, „A” a fénynyaláb átmérője a lencsén, 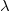 a hullámhossz az adott közegben. Az optikai rendszert diffrakció korlátosnak hívjuk, ha a geometriai optikai úton számolt szóródási folt méret kisebb, mint a diffrakciós folt.
a hullámhossz az adott közegben. Az optikai rendszert diffrakció korlátosnak hívjuk, ha a geometriai optikai úton számolt szóródási folt méret kisebb, mint a diffrakciós folt.
- Numerikus apertúra (NA): Egy hengerszimmetrikus nyaláb konvergenciáját leíró számadat, amelynek értéke definíció szerint:
![\[NA = n \cdot \sin \Theta\]](/images/math/3/a/d/3ad672a0c530cd4285001c191945589d.png)
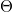 pedig a nyaláb fél-kúpszöge (lásd a 11.5.ábrát). Az NA-t lencsék vagy objektívek felbontóképességének jellemzésére szokták használni (NA nagy → felbontóképesség nagy), mivel nagyobb kúpszögek esetén a (11.15) összefüggés helyett a diffrakciós folt mérete az alábbi képlettel számolható ki:
pedig a nyaláb fél-kúpszöge (lásd a 11.5.ábrát). Az NA-t lencsék vagy objektívek felbontóképességének jellemzésére szokták használni (NA nagy → felbontóképesség nagy), mivel nagyobb kúpszögek esetén a (11.15) összefüggés helyett a diffrakciós folt mérete az alábbi képlettel számolható ki:
![\[\Delta r = \frac{{1.22{\lambda _0}}}{{2 \cdot NA}}\]](/images/math/8/d/f/8dff30ee4b604b0405c3d39f840a02b2.png)
,ahol 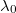 a levegőben mért hullámhossz.
a levegőben mért hullámhossz.
Néhány fontosabb aberráció jellemző képfoltja geometriai optikai közelítésben
Lencsék diffrakciós foltjának meghatározásánál alkalmazott jelölések
A (/b) és (/c) ábrán a lencse fókuszpont környéki intenzitás eloszlása látható (Airy-folt), ideális leképezés esetén.
Vastag lencsékre és paraxiális sugarakra vonatkozó közelítő összefüggések
![\[f = \frac{1}{\left (\left (n - 1\right )\left (\frac{1}{R_1} - \frac{1}{R_2} + \frac{n - 1}{n} \cdot \frac{t}{R_1 \cdot R_2}\right )\right )}\]](/images/math/d/a/0/da0f73792725f95e49812a7515a4b9ae.png)
![\[S_1 = \frac{R_1 \cdot t}{\left (n \cdot \left (R_1 - R_2\right ) -\left ( n - 1\right )t\right )}\]](/images/math/b/8/6/b8639c8954ba9646420a34f30d77c713.png)
![\[S_2 = \frac{R_1 \cdot t}{\left (n \cdot \left (R_2 - R_1\right ) +\left ( n - 1\right )t\right )}\]](/images/math/f/9/7/f97cd53dcae1e20c56cf61642f690ada.png)
ahol „f ” a lencse effektív fókusztávolsága, „n” a lencse törésmutatója, R1 és R2 a lencse első és második törőfelületének görbületi sugara, „t” avastagsága, valamint S1 a tárgy-, S2 a képoldali, azaz első és hátsó fősík helye a lencsefelületekhez képest (lásd a 11.6 ábrát).
Az alkalmazott optikai tervező program leírása
A labormérés során az OSLO LT 6.1 szoftvert használjuk, amely az optikai modellezésben és ipari lencsetervezésben széles körben használt OSLO programcsalád legegyszerűbb változata. A program oktatásra/otthoni gyakorlásra ingyenesen letölthető a http://www.lambdares.com/ honlapról. A program felhasználóbarát grafikus felülettel rendelkezik (ld. 11.7. ábra), amely három különböző ablaktípust használ:
- Lencse adatokat tartalmazó és azok szerkesztésére szolgáló táblázat (egy ablak)
- Szöveges vagy numerikus kimenetek megjelenítésére szolgáló szöveges ablak (egyszerre kettő használható)
- Képi kimenetek megjelenítésére szolgáló grafikus ablak (egyszerre több is használható)
A program kezelése legegyszerűbben a menürendszeren keresztül vagy az ablakokon található ikonokkal történhet, de rendelkezik egy parancs-sorral, ahol közvetlen utasítások is kiadhatók. A szoftver alapszintű kezelését a mérési feladatok végrehajtása során fogjuk megtanulni, ennek megfelelően annak ismertetése is ott történik.
Mérési feladatok
Végezze el az alábbi mérési feladatokat a számozás sorrendjében. Kérjük, hogy a használt lencsefájlokat ne változtassa meg és ne törölje le! A jegyzőkönyv készítéséhez használjon szövegszerkesztő programot. Az OSLO grafikus és szöveges ablakainak tartalmát jobb egérgombbal rákattintva a Copy to clipboard vagy a Copy page utasítással tudja másolni és a Szerkesztés beillesztés paranccsal a szövegszerkesztőbe illeszteni. Az adatok bevitelére használt ablakok bal felső sarkában található zöld pipával az ablakot a változtatásokat elmentve zárja be (OK), míg a piros X a változtatásokat nem veszi figyelembe (CANCEL). A szükséges grafikonok készítéséhez használjon táblázatkezelő programot! Minden egyes pontnál értelmezze / diszkutálja az eredményt!
1. feladat: A lencserendszer beolvasása
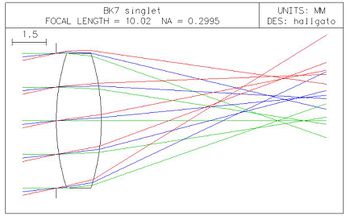
Indítsa el az OSLO LT programot a Start menü vagy az asztalon található ikon segítségével. A File menü Open lens parancsával nyissa meg a C:\Hallg mérés\singlet.len lencsefájlt. A Lens menü Lens drawing / System utasítással rajzoltassa ki a beolvasott lencsét (a felugró ablakban az eredeti beállítások megőrzéséhez válassza az OK gombot). Ugyanezt megteheti egyszerűbben a grafikus ablak tetején levő lencserendszert ábrázoló ikonra kattintva.
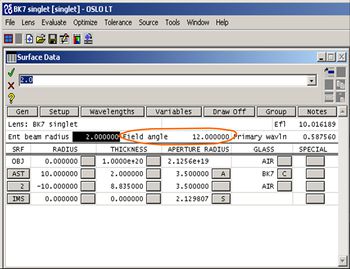
Ekkor a 11.8. ábrán bemutatott kép jelenik meg, amely fejlécében mutatja a lencse elnevezését, effektív fókusztávolságát (ld. 11.6. ábra) és a képoldali (jobb oldal) nyaláb numerikus apertúráját. Látható, hogy a rendszer egy szimmetrikus bi-konvex lencsét tartalmaz, előtte egy külön apertúra helyezkedik el. A lencsét a végtelenből jövő párhuzamos sugárnyalábok világítják meg. A nyalábok rendre 0o, 6o és 12°-os szöget zárnak be az optikai tengellyel (z-tengely). A maximális nyalábszöget (tárgyszög) a lencse szerkesztő ablak field angle cellájában tudjuk átállítani (lásd a 11.9.ábrát), a nyalábok száma, szöge és a megjelenített sugarak száma pedig a Lens menü Lens drawing conditions pontjában állítható (lásd a 11.10.ábrát).
- R1 = 10mm (C1 = 1/R1 = 0.1)
- R2 = -10mm (C2 = 1/R2 = -0.1)
- D1 = 2mm
- apertúra sugár = 3 mm
- anyag: Schott BK7 üveg
2. feladat: A beolvasott adatok ellenőrzése
A Lens menü Show Surface Data / All data utasításával listázza ki a lencseadatokat a képernyőre. Hasonlítsa össze azt 11.12.ábrán bemutatott adatokkal. Az első szakasz a lencse geometriai adatait tartalmazza (görbületi sugár, vastagság, apertúra sugár, anyag) minden egyes felületre. A program a vastagság és anyag tulajdonságot az adott anyagot megelőző felület tulajdonságaihoz rendeli hozzá. Így az első sor (a program számozása szerint 0. jelölése OBJ) a tárgysíkot írja le, amelynek 1020 mm-es vastagsága azt jelenti, hogy a tárgy a végtelenben van, azaz a lencsét párhuzamos fénysugarak világítják meg. A második sor, a program számozása szerint 1. felület, a lencse első felülete. A harmadik sor (a program számozása szerint 2) a lencse hátsó felülete és végül a negyedik a képsík. A második szakasz a különböző felületeken érvényes apertúra sugarakat (lencseátmérő fele) mutatja, harmadik a használt hullámhosszakat és azok súlyfaktorát, amellyel az adott hullámhossz az foltméret számításnál szerepel. Az utolsó két szakaszban leírja a használt üvegek törésmutatóját és áteresztését (transzmisszió) a fent definiált hullámhosszakra.
3. feladat: Szóródási foltok kirajzolása
A szóródási foltokat először egyetlen hullámhosszon vizsgáljuk. Ezért a lencse-adatokat szerkesztő ablakban kattintson a wavelengths gombra és ott törölje ki a 2. és 3. hullámhosszt, így csak egyetlen hullámhossz marad (587,56 nm). A Window menü Graphics/New parancsával nyisson új grafikus ablakot, majd az Evaluate menü Spot diagram/Report graphic utasításával rajzolja ki a lencse szóródási foltjait. A felugró ablakban adja meg az ábrázolt sugarak számát (aperture divisions), a képsíktól való maximális z irányú eltérést (max. defocus) és az ábrázolandó defókusz értékek számát a 11.13.a ábrának megfelelően. Ekkor a 11.13.b ábrán látható kép jelenik meg. Az egymás alatti három ábrasorozat rendre az optikai tengellyel 12°, 8,46° és 0°-os szöget bezáró nyalábokhoz tartozik. (Az értékeket a program az egyes sorok előtt az ábra bal oldalán tünteti fel). Egy vízszintes ábrasoron belül a középső szóródási foltot pontosan a képsíkban, az előtte illetve utána lévő két másik foltot a képsíkkal párhuzamos, de kismértékben eltolt síkokban kapjuk. Az eltolás mértéke (defókusz) a függőleges oszlopok alatt látható. Lehetőség van arra is, hogy a középső oszlopot is kitoljuk a képsíkból. Ekkor a lencse-adatokat szerkesztő ablakban az utolsó lencsefelülethez tartozó vastagság értékét kell átállítani.
Az ábra bal alsó részén egy függőleges vonal, és egy mellé írt szám mutatja a méretskálát (mm-ben) a képsíkban. Ez lehetővé teszi, hogy durván meghatározzuk a szóródási foltok méretét. Az ábra alapján hol van az optimális fókusz? Miért?
4. feladat: A szóródási folt vizsgálata a képsík helyzetének függvényében
A szóródási foltok segítségével az optikai tengellyel párhuzamos sugárnyaláb esetén rajzolja fel a szóródási folt méret - képsík defókusz görbét a ±2-mm tartományban. A görbe pontjait pl. a kinyomtatott diagramokról mérheti le. A jobb felbontás és nagyobb pontosság érdekében érdemes megnövelni az ábrázolandó defókusz (képsík eltolás) értékek és sugarak számát, valamint átállítani az ábrázolás léptékét (Scale). Kísérletezze ki a legjobb beállításokat és vegye fel a görbét. Ábrázolja a kapott eredményt!
A foltméretek pontos és gyors meghatározásához igénybe veheti a program által nyújtott automatikus számolásokat is. A fókuszfolt méretét kiszámoltathatja az Evaluate menü Spot diagram/Spot size analysis pontjában (object point 0,0,0, best focus: NO!). Az itt kapott foltsugár (GEO RMS R) az átvezetett sugaraknak a képsíkkal vett metszéspontjaiból 2D átlagot számol és meghatározza az attól való eltérés négyzetes középértékét (súlypont). Ez az ún. RMS foltméret használatos a geometriai optikai felbontás jellemzésére.
A szóródási foltméret - képsík defókusz görbe kvalitatív vizsgálatára alkalmas a lencse rendszerrajza is, ha csak az optikai tengellyel párhuzamos nyalábot ábrázoljuk nagyobb számú átvezetett sugárral (ld. Lens drawing conditions és 11.10.ábra). Rajzoltassa ki a sugarakat és a fókuszpontra zoomolva figyelje meg a fénynyaláb burkoló görbéjét (zoomolás: kijelölheti a területet a bal egérgombot lenyomva tartott egeret elhúzva). Hasonlítsa össze a foltméretekből kapott görbe és az ábra jellegét!
5. feladat: Paraxiális fókuszpont meghatározása
A program segítségével határozza meg a lencse paraxiális fókuszpontjának a távolságát, az utolsó lencsefelülettől mérve! A kapott eredményt hasonlítsa össze a vastag lencsékre és tengelymenti sugarakra érvényes közelítő formulából számított értékkel! (11.16 összefüggés). A fókuszpont helyét úgy határozzuk meg, hogy elindítunk egy, a tengellyel párhuzamos, a tengelyhez nagyon közeli sugarat és meghatározzuk a tengellyel való metszését. A sugarat az Evaluate menü Single ray trace parancsával indíthatjuk. A paramétereket a következőképpen állítsuk be:
output format: full, surface selection: all, FY=0.01, set object point 0,0,0
Ilyen módon az optikai tengellyel párhuzamos, attól (0.01  apertúra =) 0.03 mm-re haladó sugarat indítunk, és annak átvezetését a szöveges ablakban követhetjük nyomon. A szöveges ablakban megjelenő táblázat első oszlopa tartalmazza felületenként az optikai tengelytől mért távolságot (Y) és alatta az iránykoszinuszok értékeit (L). Rajzolja meg vázlatosan a sugár útját a képsík közelében és elemi geometriai módon határozza meg a tengellyel való metszéspontot. Állítsa be a képsík „vastagság” értékét úgy, hogy a képsík az így meghatározott helyre kerüljön. Próbáljon ki más, a tengelytől kicsit távolabbi sugarakat is. Figyelje meg a különbséget.
apertúra =) 0.03 mm-re haladó sugarat indítunk, és annak átvezetését a szöveges ablakban követhetjük nyomon. A szöveges ablakban megjelenő táblázat első oszlopa tartalmazza felületenként az optikai tengelytől mért távolságot (Y) és alatta az iránykoszinuszok értékeit (L). Rajzolja meg vázlatosan a sugár útját a képsík közelében és elemi geometriai módon határozza meg a tengellyel való metszéspontot. Állítsa be a képsík „vastagság” értékét úgy, hogy a képsík az így meghatározott helyre kerüljön. Próbáljon ki más, a tengelytől kicsit távolabbi sugarakat is. Figyelje meg a különbséget.
6. feladat: Nyíláshiba (szférikus aberráció, gömbi eltérés) vizsgálata
A nyíláshiba jól jellemezhető a paraxiális fókuszban mérhető nyalábátmérővel A nyalábátmérő azonos fókusztávolság és azonos lencsevastagság esetén függ a lencse görbületi sugaraitól. Határozza meg és ábrázolja a 11.1 táblázatban megadott lencsék paraxiális nyalábátmérőjét a lencsék ún. alaktényezője függvényében! A lencséket 4 mm átmérőjű, a z- tengellyel párhuzamos sugárnyalábbal világítjuk meg. A lencsék vastagsága D=2mm, törésmutatója n=1,51418 azonos. Közelítőleg azonos a fókusztávolságuk is. A szóródási foltok fölrajzoltatásával határozza meg, hogy az alaktényező mely értéknél lesz minimális a nyalábátmérő! Szükség lehet az aberrációs skála, a defókusz vagy a "Z" irányú lépésköz optimális beállítására.
A lencse adatokat szerkesztő ablakban cserélje ki a törőfelületek görbületi sugarát! Az előzőek szerint határozza meg a minimális nyalábátmérőt a táblázatban szereplő összes lencsére! A nyalábátmérő meghatározásához igénybe veheti a program által nyújtott automatikus számolásokat. A paraxiális fókusz pontos beállításához (a konfiguráció minden megváltoztatása után!) kattintson a képsík vastagságértéke mellett jobbra található téglalapra és válassza az Autofocus – paraxial focus utasítást. A fókuszfolt méretét ezentúl pontosan kiszámoltathatja az Evaluate menü Spot diagram/Spot size analysis pontjában (object point 0,0,0, best focus: NO!). Az itt kapott foltsugár (GEO RMS R) az átvezetett sugarak a képsíkkal való metszéspontjaiból 2D átlagot számol (folt súlypontja) és meghatározza az attól való eltérés négyzetes középértékét. Ez az ún. RMS foltméret használatos a geometriai optikai felbontás jellemzésére. Az előzőektől különböző foltméretet kap, ha az az Autofocus – paraxial focus helyett az az Autofocus – Minimum RMS spotsize-On axis (monochromatic) beállítást választja. Magyarázza a különbséget!
Ábrázolja a foltméretet az alaktényező függvényében a paraxiális és a legkisebb foltméretet adó valós fókuszpontban is! Minden lencseátmérő 6 mm legyen!
![\[ \begin{array}{|c|c|c|} \hline {\bf R_1(mm)} & {\bf R_2 (mm)} & {\bf S} \\ \hline inf & -5.00 & -1.00 \\ \hline 10 & -10 & -0.00 \\ \hline 5.0 & inf & 1 \\ \hline 3.33 & 10 & 2 \\ \hline \end{array} \]](/images/math/7/1/4/7140f56c774d8974b1384a4eba5fee98.png)
![\[11.1.\ t\acute{a}bl\acute{a}zat.\ Lencseadatok\ a\ 6.\ feladathoz\]](/images/math/c/b/5/cb5a3e6f964571a4433d60a0396347aa.png)
Hasonlítsa össze a fenti foltméreteket az előzőeknek megfelelő fókusztávolságú és apertúrájú belépő oldalán aszférikus felülettel határolt fókuszáló lencse (C:\Hallg mérés\singlet_asphere.len) által adott szóródási folttal. A példa mutatja, hogy egy aszférikus felülettel a gömbi eltérés igen jól korrigálható.
7. feladat: A kóma hiba tanulmányozása
Növelje meg a tárgyszöget (Field angle) 20°-ra és a 3. feladathoz hasonlóan rajzolja fel ismét a szóródási foltokat. Az ábra szemléletesen mutatja az úgynevezett kómát (üstökös hibát). A sugarak és az optikai tengely által bezárt szög növelésével a képsíkon egy jellegzetes üstökös szerű képet kapunk. A képnek van egy erősen megvilágított középső foltja („az üstökös magja”). Ezt a lencserendszerbe belépő nyaláb középső tartományán áthaladó fénysugarak alakítják ki. A belépő nyaláb szélén haladó sugarak egy sokkal kisebb intenzitású, de a mag méreténél kétszer háromszor nagyobb területre szóródnak szét. A tárgyszög növelésével a mag középpontja és a farokrész eltolódik.
A belépő nyalábban koncentrikus körökben elhelyezkedő sugarak átvezetésével még szemléletesebb képet kapunk (Evaluate menü Spot diagram– Recipolar spot diagram). Egy sajnálatos programhiba miatt ezen utasítás nem engedi a képszög állítását, így a 20 fokos tárgyszögre akkor kapja a megfelelő ábrát, ha előtte pl. Spot diagram– single spot diagram utasítást hajt végre és ott beállítja a kívánt relatív képszöget (set object point, FBY=1) A tengellyel párhuzamos sugarak esetén jól láthatók a körök, amelyek a szög növelésével már eltorzulnak és nem koncentrikusak, az egyre nagyabb sugarú körökből érkező fénysugarak egyre jobban eltolódnak a kisebb sugarú körökből származó fénysugarakhoz képest. Rajzoltassa ki az így kapott szóródási foltot!
8. feladat: Színi hiba vizsgálata
Olvassa be újra a singlet.len fájlt (kilépésnél NE mentse el a lencsefájl változásait!). A lencse úgynevezett BK7-s üvegből készült. A lencsét 6 mm átmérőjű fehér színű sugárnyalábbal világítjuk meg. Az üveg törésmutatóját a hullámhossz függvényében a 11.2 táblázatban adtuk meg. Az előzőekben sárga fényben meghatároztuk a fókuszpont helyét. Becsülje meg a folt növekedését, ha mindhárom hullámhosszt figyelembe vesszük.
Rajzoltassa ki a szóródási foltokat három színre. Hasonlítsa össze a 3. feladatban kapott eredményekkel
| Szín | Hullámhossz (μm) | Törésmutató |
|---|---|---|
| vörös | 0.65628 | 1.51418 |
| sárga | 0.58959 | 1.51666 |
| kék | 0.48613 | 1.52225 |
![\[11.2.\ t\acute{a}bl\acute{a}zat.\ Korona\ddot{u}veg\ t\ddot{o}r\acute{e}smutat\acute{o}ja\ k\ddot{u}l\ddot{o}nb\ddot{o}z\ddot{o}\ hull\acute{a}mhosszakra\]](/images/math/9/4/5/9450a5ec98572014ce7709f77bb8252c.png)
9. feladat: Diffrakciós korlát vizsgálata
Olvassa be a tessar.len fájlt, mely a 11.15. ábrán látható adatokkal jellemzett lencsét tartalmazza. A rendszer rajzát a 11.14. ábrán mutatjuk be. A lencseadatok kilistázásával ellenőrizze a paramétereket.
A lencsehibák abból adódnak hogy gömbfelületekkel nem lehet ideális hibamentes leképezést megvalósítani. Ez azt jelenti, hogy egy geometriai pont képe nem pont, hanem a lencse paramétereitől függő kisebb vagy nagyobb tartomány. A hiba jelentősen csökkenthető ha bonyolult optimalizációs eljárás eredményeképpen több gömbfelületből álló lencserendszert alkalmazunk. A tessar.len fájlból beolvasott négytagú rendszer is ilyen. Ezek a rendszerek azonban csak az optimalizálásnál figyelembe vett tárgyszögnél kisebb szögekre, és az optimalizálásnál használt belépő nyaláb méret esetén működnek megfelelően. Ettől kismértékben eltérve a rendszer tulajdonságai rohamosan romlanak.
A geometriai optikai hibák és a képfolt mérete jelentősen csökkenthető a belépő nyaláb méretének csökkentésével. Az alábbiakban megvizsgáljuk, hogy meddig kell csökkenteni az előzőekben vázolt optimalizált lencserendszer apertúráját ahhoz, hogy a rendszer a tengellyel párhuzamos nyalábra diffrakciókorlátos legyen.
A belépő nyaláb méretét a lencse szerkesztő ablak Ent beam radius pontja alatt változtathatjuk meg. A fájlból beolvasott rendszer belépő nyaláb sugara 15 mm. Csökkentse ezt addig, míg a fókuszpontban a szóródási folt mérete a (11.15) összefüggéssel megadott diffrakciós korlát alá süllyed. A belépő nyaláb méret módosításával változik a diffrakciós foltméret is. Ezért ezt minden módosítás után újra kell számolni. Ábrázolja az RMS foltméretet és a diffrakciós foltméretet a belépő nyaláb sugarának függvényében tengellyel párhuzamos nyalábokra. Határozza meg azokat a belépő nyaláb méreteket, amely mellett a rendszer diffrakció-korlátos.
A valódi, kísérletileg mérhető intenzitáseloszlást természetesen a geometriai és a diffrakciós effektusok együttes figyelembevételével lehet megkapni. Ezt a program úgy számolja ki, hogy a geometriai hibák által eltorzított és a rendszer apertúrája által levágott hullámfrontot Fourier transzformálja és azt négyzetre emeli. Az így kapott intenzitáseloszlást pontszórásfüggvénynek nevezzük (Point spread function: PSF).
Vizsgálja meg a pontszórásfüggvényt legalább három apertúra értékre: a teljes apertúrára, az előző pontban megállapított diffrakciós határra, és egy annál lényegesen kisebb apertúrára. A programban ezt az Evaluate menü Spread Function – Plot PSF map paranccsal teheti meg. Melyik esetben nevezné a rendszer felbontását a legnagyobbnak? Miért?
10. feladat: Képmező hajlás tanulmányozása
Az előző pontban vizsgált lencserendszernél állítsa be a belépő nyaláb sugarát 15 mm-re, és töröljön ki 2 hullámhosszat, hogy monokromatikus esetben vizsgálhassa a rendszert. Rajzoltassa ki a szóródási foltokat 3. pontban leírtakhoz hasonlóan. Állítsa be úgy a maximális defókuszt és a „Z” irányú lépésközt, hogy mind a három tárgyszögre egyszerre legyen látható a legkisebb képfolt. A képmező elhajlást a 0°-os és a 15°-os irányokhoz tartozó minimális foltok „Z”- irányú távolságával jellemezhetjük. Határozza meg ezt az értéket!
PDF formátum