„Félvezető fotodetektorok” változatai közötti eltérés

A Fizipedia wikiből
a
 
(2 szerkesztő 122 közbeeső változata nincs mutatva)
21. sor: 21. sor:
  
 
__TOC__
 
__TOC__
−
 
−
'''''Szerkesztés alatt!'''''
 
  
 
==Elméleti összefoglaló==
 
==Elméleti összefoglaló==
34. sor: 32. sor:
  
 
Egy tökéletes sugárforrás - ún. feketetest - elektromágneses emisszióját a Planck-törvény írja le:
 
Egy tökéletes sugárforrás - ún. feketetest - elektromágneses emisszióját a Planck-törvény írja le:
 +
$$M_{e,\lambda } \left (\lambda, T\right ) {{=}} \frac{2\pi hc^2}{\lambda^5\left (e^{\frac{hc}{\lambda kT}}-1\right )}$$
 +
ahol
 +
* $M_{e,\lambda}\left (\lambda, T\right ) \left [Wm^{-3} \right ]$ a felületegység által kisugárzott spektrális sugárzási teljesítmény,
 +
* $\lambda [m]$ az emittált hullámhossz,
 +
* $T[K]$ az abszolút hőmérséklet,
 +
* $h {{=}} 6,62 \cdot 10^{-34} Ws^{2}$ a Planck állandó,
 +
* $c[m/s]$ a fénysebesség, és
 +
* $k {{=}} 1,38 \cdot 10^{-23} WsK^{-1}$ a Boltzmann állandó.
 +
A teljes hulllámhossz tartományon kisugárzott teljesítményt a Stefan-Boltzmann törvény adja:
 +
$$M_e\left (T\right ) {{=}} \int\limits_0^\infty M_{e,\lambda} \left (\lambda ,T\right )d\lambda {{=}} \sigma_eT^4$$
 +
ahol $\sigma_e {{=}} \frac{2\pi^5k^4}{15h^3c^2} {{=}} 5,67 \cdot 10^{-8} Wm^{-2}K^{-4}$
 +
 +
A kisugárzott teljesítmény helyett a $\lambda$ hullámhosszú foton ($hc/\lambda$) energiájának figyelembevételével megkaphatjuk az egységnyi felület teljes kisugárzott fotoáramát.
 +
$$M_p\left (T\right ) {{=}} \int\limits_0^\infty M_{e,\lambda} \left (\lambda ,T\right )\frac{\lambda}{hc}d\lambda {{=}} \sigma_pT^3$$
 +
ahol $\sigma_e {{=}} 1,52 \cdot 10^{15} fotons^{-1}m^{-2}K^{-3}$.
 +
 +
A Wien-féle eltolási törvény kapcsolatot teremt a hőmérséklet és a kisugárzott teljesítmény hullámhossz-szerinti maximuma között:
 +
$$\lambda T\Big| _{\frac{\partial M_{e,\lambda}}{\partial \lambda} {{=}} 0} {{=}} 2898\ \mu mK$$
 +
Egy valós anyag spektrális emisszióképességét az anyag által adott $\Omega$ térszögbe kisugárzott teljesítmény és a tökéletes fekete test által kisugárzott teljesítmény hányadosa adja:
 +
$$\epsilon \left (\Omega,\lambda,T\right ) {{=}} \frac{L_{e,\lambda}(\lambda,T)_{anyag}}{L_{e,\lambda}(\lambda,T)_{fekete\ test}} {{=}} \epsilon_e(\lambda)$$
 +
ahol $L_{e,\lambda} {{=}} M_{e,\lambda}/\Omega$.
 +
 +
Megjegyzendő, hogy míg a spektrális fotonkibocsátás és az emisszióképesség minden esetben megegyezik,
 +
$$\epsilon_e(\lambda) {{=}} \epsilon_p(\lambda)$$
 +
az egész spektrumon integrált teljes emisszió általában nem azonos:
 +
$$\epsilon_e {{=}}\frac{\int\limits_0^\infty\epsilon_e(\lambda)L_{e,\lambda}(\lambda,T)d\lambda}{\int\limits_0^\infty L_{e,\lambda}(\lambda,T)d\lambda} \neq \epsilon_p$$
 +
 +
Az elektromágneses sugárzás Kirchoff-törvénye szerint termikus egyensúlyban az emittált és abszorbeált energia megegyezik:
 +
$$\alpha(\lambda) {{=}} \epsilon (\lambda)$$
 +
 +
Egy tetszőleges felületre beeső optikai nyaláb viselkedését három tényező írja le a következő módon:
 +
$$\alpha + r + t {{=}} 1$$
 +
 +
ahol r és t a reflexió, illetve a transzmisszió. Tökéletes fekete test esetén $\epsilon(\lambda) {{=}} 1$, vagyis $\alpha {{=}} 1$, így $r+t {{=}} 0$.
 +
 +
Minden sugárforrás esetén fellép valamilyen bizonytalanság a kibocsátott elektromágneses sugárzás mennyiségében, melyet csak statisztikusan írhatunk le. n foton kibocsátásának valószínűségét a Poisson-eloszlás jól közelíti:
 +
$$P_{\tau} (n) {{=}} \frac{n^{-n}}{n! \cdot e^{\overline{n}}} \qquad\overline{n} {{=}} \sum\limits_nP_{\tau}(n)n$$
 +
ahol $\tau$ a vizsgált időintervallum, és
 +
 +
$\overline{n}$ a $\tau$ idő alatt kibocsátott fotonok átlagos száma.
 +
 +
A detektált fotonok száma a kibocsátási folyamat diszkrét volta miatt binomiális eloszlást követ, mely nagyszámú megfigyelés esetén a Poisson-eloszláshoz közelít. A megfigyelő detektor m számú fotont érzékel, ha kvantumhatásfoka kisebb, mint egységnyi:
 +
$$P_{\tau} (m) {{=}} \frac{{\left (\eta \overline{n}\right )}^{-n}}{m! \cdot e^{\eta\overline{n}}} \qquad\eta {{=}} \frac{\overline{m}}{\overline{n}}$$
 +
ahol $\overline{n}$ a detektorra érkező fotonok átlagos száma, és
 +
 +
$\eta$ a detektor kvantumhatásfoka.
 +
 +
Az előzőekből következik, hogy egy tökéletesen zajmentes detektorral sem lehet végtelen jel/zaj viszonyt elérni. A sugárzás statisztikus volta meghatározza az elméletileg elérhető jel/zaj viszonyt:
 +
$$SNR {{=}} \frac{\overline{n}}{\delta} {{=}} \sqrt{\overline{n}}$$
 +
 +
ahol $\delta {{=}} \sqrt{\overline{n}}$ a Poisson-eloszlás szórása. Nem egységnyi kvantumhatásfokú detektor esetén:
 +
$$SNR {{=}} \frac{\eta\overline{n}}{\sqrt{\eta\overline{n}}} {{=}} \sqrt{\eta\overline{n}}$$
 +
 +
A detektor megfigyelt jel/zaj viszonya soha nem lehet jobb, mint az előző összefüggésben megadott érték.
 +
 +
===Félvezető detektor működése===
 +
A fény kvantumos természetének következtében a fémek ionizációja akkor következik be, ha a foton $E_p$ energiája meghaladja a fémben az elektron $\phi$ kilépési munkáját (fotoelektromos jelenség):
 +
$$E_p {{=}} h\nu \geq \phi$$
 +
 +
A fotonok detektálhatóságát a fotonenergia és az anyag megengedett elektronenergia állapotainak kapcsolata határozza meg. Szilárdtestben az egyetlen atomra jellemző állapotok nagyszámú, egymáshoz közeli állapotokra - sávokra - hasadnak. Abszolút nulla fokon a legmagasabb betöltött energiaszintet $E_F$ Fermi-szintnek nevezzük. A kilépési munka:
 +
$$\phi {{=}} E_i - E_F$$
 +
 +
ahol $E_i$ az elektron ionizációs energiája. Magasabb hőmérsékleten a Fermi-szint megadja azt az energiaszintet, ahol a betöltési valószínűség 50%. Az egyes $E_n$ energiaállapotok $P(E_n)$ betöltési valószínűségét az elektronokra érvényes Fermi-Diac eloszlás adja:
 +
$$P\left (E_n\right ) {{=}} \frac{1}{e^{\frac{E_n - E_f}{kT}}+1}$$
 +
 +
Az [[#fig:1|1. ábra]] tünteti fel a fémekben az elektronok eloszlását, a legfelső betöltetlen energiasávban,
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|Fotodet_01.png|fig:1|1. ábra Fémek elektroneloszlása}}
 +
| {{fig|Fotodet_02.png|fig:2|2. ábra Félvezetők megengedett állapotai}}
 +
|}
 +
 +
A szigetelők és a félvezetők sávszerkezete eltér a fémekétől, a vezetési (T = 0 K -en üres) és a vegyérték sáv egymástól elválik, közöttük széles tiltott sáv helyezkedik el. Az anyag mindaddig szigetelő, amíg a termikus energia kellően alacsony:
 +
$$kT \ll E_g$$
 +
Megjegyzendő, hogy a Fermi-szint közelítőleg a tiltott sáv felénél helyezkedik el. Termikus gerjesztés esetén az elektron a vezetési sávba kerül és egy pozitív töltésű lyukat hagy maga után, mely szintén hozzájárul az áramszállításhoz. Termikus egyensúly esetén az elektron és lyuk koncentráció megegyezik és az intrinsic (adalékolatlan) töltéshordozó-koncertráció az alábbi módon számolható:
 +
$$n_i^2 {{=}} np {{=}}4\left ({\frac{2\pi \sqrt{m_n^*m_p^*}kT}{h^2}}^3\right )e^{-\frac{E_g}{kT}}$$
 +
ahol n<sub>i</sub>, n<sub>p</sub> intrinsic, elektron és lyuk töltéshordozó koncentráció,
 +
 +
$m_n^*$, $m_p^*$ elektron és lyuk effektív tömeg.
 +
 +
A vezetés az alábbi módon adható meg pl. elektronokra:
 +
$$\sigma {{=}} nq_e\mu_n$$
 +
ahol $q_e$ az elektron töltése és $\mu_n$ az elektronmozgékonyság:
 +
$$\mu_n {{=}} \frac{\nu_d}{E_0} {{=}} \frac{q_e}{m_n^*}\overline{\tau}$$
 +
amely arányos a töltéshordozók $\nu_d$ driftsebességének és az alkalmazott $E_0$ külső térerősségnek a hányadosával, illetve felírható az ütközések közötti $\overline{\tau}$ átlagos idő és az effektív tömeg segítségével.
 +
 +
Termikus gerjesztés mellett más, (pl. foton-} gerjesztésre is kerülhet töltéshordozó a vezetési sávba, ha a foton energiája:
 +
$$h\nu \geq E_g$$
 +
A leggyakoribb optikai detektálási mód, hogy mérjük az eszköz vezetőképességét (vagy ellenállását: fotokonduktív detektorok).
 +
 +
Az extrinsic ("külső vezetésű") félvezetők a kristályrácsba beépített adalékatomok hatása következtében válnak vezetővé. Az adalékatomok donorok, ha negatív töltésfelesleget visznek be a kristályba, akceptorok, ha pozitívat. A [[#fig:3|3.]] és [[#fig:4|4. ábra]] mutatja az adalékolt félvezetők sávszerkezetét.
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|Fotodet_03.png|fig:3|3. ábra A donorok hatása a sávszerkezetre}}
 +
| {{fig|Fotodet_04.png|fig:4|4. ábra Az akceptorok hatása a sávszerkezetre}}
 +
|}
 +
Az ábrák illusztrálják a Fermi-nívó eltolódást is. Megfelelő adalékolás esetén a félvezető vezetési tulajdonságai nagymértékben függetlenné válnak a hőmérséklettől, mivel így a vezetést nem a termikusan gerjesztett, hanem az adalékolás hatására a tiltott sáv szélességénél jóval kisebb energiával a vezetési sávba gerjesztett donor elektronok, illetve az akceptor szintek gerjesztettsége miatt a vegyértéksávban létrehozott lyukak biztosítják.
 +
 +
Ha p-n átmenetet hozunk létre különböző vezetési típusú félvezetőkből, az egyensúly beállításához szükséges a Fermi-szintek kiegyenlítődése, ahogy az az [[#fig:5|5. ábrán]] látható. Ez potenciálkülönbséget  hoz létre a p-n átmeneten, melynek egyensúlyi értéke:
 +
$$\phi_0 \approx \frac{kT}{q_e}ln\frac{n_pp_n}{n_i^2}$$
 +
ahol $n_p$ az elektronkoncentráció a p-tartományban és
 +
 +
$p_n$ a lyukkoncentráció az n-tartományban melyeket kisebbségi töltéshordozónak nevezünk.
 +
 +
A kisebbségi töltéshordozók jelenlétét azok ellentétes tartományból történő diffúziója okozza. A diffúzió következtében a p-n átmenet közelében a töltéshordozó-koncentráció csökken, vagyis kiürített tartomány jön létre, mely a - pozitív, illetve negatív atomtörzsek révén biztosítja a Fermi-nívó  kiegyenlítéséhez szükséges $\phi_0$  potenciálkülönbséget.
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|Fotodet_05.png|fig:5|5. ábra A p-n átmenet}}
 +
|}
 +
Külső nyitófeszültség hatására (n-oldalra negatív, p-oldalra pozitív feszültséget kapcsolva), a kiürített réteg szélessége, így $\phi_0$  értéke csökken, az átmeneten áthaladó áram pedig exponenciális függvény szerint növekszik. Fordított irányú - zárófeszültség esetén $\phi_0$ , értéke növekszik, az áram pedig csökken. Ebben az esetben jelentőssé válik a - kisebbségi töltéshordozók által szállított - zéróirányú, ún. visszáram. Külső, pl. fotongerjesztéssel a visszáram értéke jelentősen nő, a gerjesztés révén keletkező kisebbségi töltéshordozó-párok miatt. Ezen az elven működnek az ún. fotovoltaikus detektorok.
 +
 +
Érdemes megjegyezni, hogy a félvezető eszközökben az áramot kétféle hatás alakítja ki, melyekkel a teljes j áramsűrűség elektronokra és lyukakra (vektoriális formában):
 +
$$j_n {{=}} +q_eD_ngradn + q_en\mu_nE$$
 +
$$j_p {{=}} -q_eD_ngradp + q_en\mu_pE$$
 +
 +
Az egyenletek első tagja a töltéshordozó-koncentráció eltérésből eredő gradiens okozta diffúziót írja le. A D diffúziós állandó kifejezése az ún. Einstein-összefüggéssel lehetséges:
 +
$$D_{n,p} {{=}} \frac{kT}{q_e}\mu_{n,p}$$
 +
 +
Az áramsűrűség másik összetevője a külső E térerősség hatására létrejövő ún. drift, mely a vezetőképességgel kifejezve:
 +
$$j_{n,p,E} {{=}} \sigma_{n,p}E$$
 +
 +
===Detektálási mechanizmusok===
 +
A két alapvető detektálási mód a fotokonduktív és a fotovoltaikus, mindkettő a belső fotoeffektuson alapul.
 +
 +
A fotokonduktív detektor elektronjai megfelelő energiájú foton hatására gerjesztődnek, vagyis nő a vezetésben résztvevő töltéshordozók koncentrációja, így az eszköz vezetőképessége változik:
 +
$$\Delta \sigma {{=}} \Delta nq_e\mu_n$$
 +
 +
Fotovoltaikus esetben a beérkező fotonok hatására a p-n átmenetben töltéshordozó párok keletkeznek, és az elektronok a p-rétegből az n-rétegbe, a lyukak az n-ből a p-rétegbe vándorolnak, a kiürített réteg által létrehozott elektromos tér hatására. Ennek következtében megváltozik a p-n átmenet feszültség-áram karakterisztikája a [[#fig:6|6.ábrának]] megfelelően.
 +
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|A fotovoltaikus detektor I-U görbéje.JPG|fig:6|A fotovoltaikus detektor I-U görbéje 6. ábra}}
 +
|}
 +
 +
A görbe alapján a detektor működhet záróirányban előfeszítve (III. síknegyed), vagy rövidzárban (IV. síknegyed), pl, műveleti erősítő bemenetére kapcsokra, mert így a fotoáram a fotonfluxus lineáris függvénye, hiszen a detektordinamikus ellenállása ekkor állandó hőmérsékleten állandó:
 +
$$R_d {{=}} \frac{\partial U}{\partial I}\bigg \vert_{U=0} {{=}} \frac{\beta kT}{q_eI_0}e^{-\frac{q_eU}{\beta kT}}\bigg \vert_{U=0} {{=}}\ \acute{a}lland\acute{o}$$
 +
 +
A harmadik típusú detektor a fotoemissziós elvet alkalmazza, vagyis működése ~a fotoelelektromos hatáson (direkt fotoeffektus) alapul. Ebben az esetben az alacsony kiléoési munkájú ún. fotokatódból kilépő elektron biztosítja a fotoáramot (pl. fotoelektronsokszorozó fotokatódja). E három típuson kívül még sokféle működési mechanizmus létezik, melyeken hely hiányában nem tárgyalunk (bolométerek, piezoelektromos detektorok, stb.).
 +
 +
===A detektorok  jellemzői===
 +
A következőkben definiált mennyiségek (spektrális érzékenység, NEP, SNR és detektivitás) az egyes detektorok paramétereinek összehasonlítására szolgálnak adott feladat esetén. Feladattól függően igen sokféle jellemző mennyiség definálható, itt csak a legfontosabbakat említjük meg.
 +
 +
'''Spektrális érzékenység''': a detektor kimenő jelének és a beeső sugárzási teljesítménynek a hányadosa:
 +
$$\Re_u (\lambda ) {{=}} \frac{u_{ki}}{\phi_e (\lambda )} \qquad vagy \qquad \Re_i (\lambda ) {{=}} \frac{i_{ki}}{\phi_e(\lambda )}$$
 +
 +
ahol u<sub>ki</sub>[V], a detektor kimeneti  jelfeszültsége,
 +
 +
vagy i<sub>ki</sub>[A] , kimeneti jeláram,
 +
 +
és $\phi_e(\lambda[W])$, a beeső spektrális fényteljesítmény.
 +
 +
'''NEP''': zaj egyenértékű teljesítmény (noise equivalent power), dimenziója [W] az a legkisebb fényteljesítmény, amely egységnyi jel/zaj viszonyt produkál.
 +
 +
Ekkor a kimenő jel (pl. i<sub>ki</sub> )  nagysága megegyezik a kimenő zaj "rms" (négyzetes közép-} értékével:
 +
$$SNR {{=}} \frac{i_{ki}}{i_{rms}} {{=}} \frac{\Re_i\phi_c}{i_{rms}} \qquad SNR {{=}} 1 {{=}} \frac{\Re_iNEP}{i_{rms}}$$
 +
 +
'''Detektivitás:'''
 +
$$D {{=}} \frac{1}{NEP}[W^{-1}]$$
 +
 +
'''Jel/zaj viszony''' (SNR - signal-to-noise ratio): a kimenő jel és az "rms" zaj hányadosa. Az SNR értéke mindig kisebb, mint a zajmentes detektorra a 2. részben definiált SNR.
 +
 +
A detektorzaj forrásai a következők:
 +
* Foton-zaj (a sugárzási zaj)
 +
* Detektor által generált zaj (Johnson-, 1/f-, hőmérsékleti-, stb.)
 +
* Áramköri zaj (hasonlóan a b. ponthoz)
 +
 +
===Képérzékelő eszközök===
 +
A képérzékelő eszközök a fotodetektorok általánosításának is tekinthetők annyiban, hogy a kimenő jel nemcsak a felületet ért átlagos megvilágításról, hanem annak térbeli eloszlásáról is ad információt. Így a képérzékelő eszközök is - az egyszerű detektorokhoz hasonlóan - csoportosíthatók a fény-anyag kölcsönhatás (a detektálás mechanizmusa} szerint. Egy másik csoportosítás szerint a fotodetektorok integráló és nem integráló típusú eszközökre oszthatók. Ebben az esetben, bár a detektálási mechanizmusok ugyanazok, a kimenő jel információtartalma eltérő az egyes eszközökben. Ennek különösen impulzus, vagy egyéb, időben változó fényintenzitás-eloszlások detektálásakor van jelentősége. A mérés során kétféle detektorral ismerkedünk meg, egy integráló típusú ún. CCD detektorsorral és egy nem integráló típusú ún. analóg pozícióérzékelő detektormátrixszal.
 +
 +
====Lineáris (CCD) detektorsorok====
 +
 +
A jelfeldolgozó és képfelvevő eszközök területén a töltéscsatolt eszközök (CCD - charge coupled device) megalkotása nyitott új perspektívát az 1970-es évek elején. Működésük alapja, hely periódikus fém-szigetelő-félvezető (MIS - metal-insulator-semiconductor) struktúrában lehetőség van töltéscsomagok létrehozására. A töltéstárolás mechanizmusát a MIS kapacitás modell alapján, a töltéstovábbítást pedig a szabad elektron modell alapján lehet tárgyalni. A megvalósított eszközökben a detektorelemek térben mindig elkülönülnek a kiolvasó shift regiszterektől.
 +
 +
A [[#fig:7|7. ábra]] a lineáris szilárdtest képérzékelők négy alapvető fajtáját szemlélteti. A felső sorban a két alapvető kiolvasási mód (digitális shift regiszterrel vezérelt analóg kapcsolók, ill. analóg CCD shift regiszter), az alsó sorban pedig a két alapvető érzékelő elemtípus (diffúzióval előállított fotodióda, ill. MOS kapacitás) metszete látható- Az ábrán A, B, C és D betűvel jelöltük a kétféle kiolvasási mód és a kétféle ~detektortípus lehetséges négy kombinációját
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|A lineáris detektorsorok fajtái.JPG|fig:7|A lineáris detektorsorok fajtái 7. ábra}}
 +
|}
 +
 +
Az „A" esetben diffúzióval előállított p-n átmenetet tartalmazó fotodióda a detektor. Digitális shift regiszter kapcsolja egymás után a kimenetre a detektorokat. Ez az elrendezés az ún. "self-scanned" fotodiódasor (SSPD). A "B" elrendezésben (CCD detektorsor) a töltések a poliszilícium elektróda alatt létrejövő inverziós rétegben képződnek, amit pixelnek (elemi képpontnak) hívnak. A pixelekből az információ átírása párhuzamosan történik egy analóg shift regiszterbe, amelynek a kimenetén a soros videojel jelenik meg. A "C" és "D" elrendezés a kétféle detektor és a kétféle kiolvasási mód további kombinációja. A "D" típus az ún. CCPD (töltéscsatolt fotodióda). 1987-ben fejlesztettek ki egy új típusú, ún. FOTOFET érzékelő elemekből felépített különlegesen nagy dinamikájú detektorsor családot. (Detektordinamikán a maximálisan megengedhető és a minimálisan detektálható optikai jel arányát értjeük. A FOTOFET a Dalsa cég szabadalma, felépítését tekintve egy hagyományos p-n átmenetes és n-csatornás MOS struktúrájú fotodióda kombinációja, míg a töltéskiolvasás módja a CCD detektorsorban alkalmazotthoz áll a legközelebb.
 +
 +
A mérésben használt detektorsor is egy Dalsa cég által gyártott - igen nagy dinamikatartománnyal rendelkező (névlegesen 10<sup>6</sup>:1) - típus. Ennek ára viszont, hogy az eszköz karakterisztikája nem lineáris a teljes tartományban, hanem nagy intenzitásoknál logaritmikus. Ennek következtében viszont nem lép fel az ún. blooming (foltkiszélesedési) jelenség. (Nagy intenzitásoknál ugyanis a töltések távolabbi pixeleken is megjelennek - töltésszétfolyás -, így az egész detektorsor telítésbe kerülhet!) A sor 2048 elemi képpontot tartalmaz, melyek távolsága és szélessége is $16\ \mu m$. A páros és páratlan képpontok kiolvasására egy-egy analóg shift regisztereket tartalmazó csatorna áll rendelkezésre.
 +
 +
====Az analóg pozícióérzékelő detektor (PSD)====
 +
Az analóg pozícióérzékelő detektorok (PSD) kb. 1984-ben jelentek meg először. Ezek nem valódi képérzékelő eszközök, mivel csak a rájuk eső intenzitáseloszlás súlypontjának koordinátáját képesek megmérni. A PSD eszköz három rétegből áll ([[#fig:8|8. ábra]]): p-, n-, és i-típusúból. Ezeket a rétegeket egy Si szeleten hozzák létre. Ha a felületre fényfolt esik, az időegység alatta fényteljesítménnyel arányos mennyiségű töltéshordozót generál a beesés helyén. A töltések a p-típusú ellenállásrétegen keresztül haladnak az elektródák felé. Mivel a p-réteg ellenállása egyenletes, az elektródákon kifolyó áram fordítottan arányos a beesési pont és az elektróda közt mérhető távolsággal.
 +
 +
Ha a két elektróda távolsága 2L, a kifolyó teljes áram  , akkor a középponttól mért pozíciót a következő összefüggésekkel kaphatjuk meg:
 +
$$I_1 {{=}} I_0\cdot\frac{L - x}{2L} \qquad I_2 {{=}} I_0\cdot\frac{L + x}{2L} \qquad \frac{I_2 - I_1}{I_2 + I_1} {{=}} \frac{x}{L}$$
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|Az analóg pozícióérzékelő detektor (PSD).JPG|fig:8|Az analóg pozícióérzékelő detektor (PSD) 8. ábra}}
 +
|}
 +
 +
A fenti összefüggések igazak tetszőleges intenzitáseloszlás eredő súlypontjának meghatározásánál is. A PSD eszközök (lehetnek egy- vagy kétdimenziósak is. A torzítás csökkentésére és a felbontóképesség javítására a kétdimenziós eszközöknek javított változatai is lehetnek, de valamennyinél azonos a működés alapelve.
 +
 +
====A PSD és CCD detektorok paramétereinek összehasonlítása====
 +
=====Spektrális érzékenység=====
 +
A PSD eszközök spektrális érzékenysége - a Si-ból készült szilárdtest képérzékelő eszközökhöz hasonlóan - kb. $0,4\ \mu m$-től $1,1\ \mu m$-ig terjed, tehát pl. $1,06\ \mu m$ hullámhosszú Nd-YAG lézer fényt még jól detektálják.
 +
 +
=====Felbontás=====
 +
Ezt a paramétert általában a fényfolt legkisebb detektálható elmozdulásával definiálják. Az irodalom szerint a felbontás független a foltmérettől és arányos a detektort ért  megvilágítással. Mivel a PSD eszközökben a pozíciót amplitúdóméréssel  lehet meghatározni, a felbontást jelentősen befolyásolja a detektorhoz kapcsolódó elektronikus rendszer zaja is. A katalógusok ezért mindig megadják a mérési körülményeket is, pl.:
 +
* fényforrás: LED (900 nm),
 +
* fényfolt mérete:  $200\\mu m$ átmérő,
 +
* frekvencia: 10 kHz,
 +
* fotoáram:  $1\ \mu A$,
 +
* elektronika bemenő zaja:$10\ \mu V$ (sávszélesség 10 kHz).
 +
 +
Ilyen feltételek mellett típustól függően egy irányban 1000-10000 diszkrét pontnak megfelelő felbontás mérhető.
 +
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| {{fig|PSD detektorok tipikus torzítása.JPG|fig:9|PSD detektorok tipikus torzítása (A vonalak közötti valós távolság konstans) 9. ábra}}
 +
|}
 +
 +
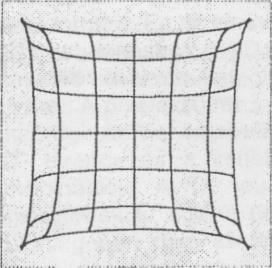
Itt kell megemlíteni a kétdimenziós PSD eszközök egy jelentős hátrányát a detektormátrixokkal szemben. Ez a paraméter a geometriai torzítás. A diszkrét érzékelőjü szilárdtest eszközöknek gyakorlatilag nincs geometriai torzítása, mivel a gyártástechnológia igen pontos mérettartást tesz lehetővé a teljes felületen. A kétdimenziós PSD eszközök esetében a szélek felé haladva már nem lineáris az összefüggés a fényfolt tényleges elmozdulása és az áramokból meghatározott érték között. A [[#fig:9|9. ábrán]] látható egy tipikus mért torzítási görbesereg, amelynek segítségével a mérőkészüléket kalibrálni kell. Az újabb fejlesztésű - korrigált geometriával rendelkező - eszközök torzítása lényegesen kisebb.
 +
 +
=====Dinamika=====
 +
A PSD eszközök lineáris tartományát felülről a maximális fotoáram korlátozza, alulról pedig a sötétáram. A maximális fotoáram minden típusnál ugyanaz (kb. 1 mA), a sötétáram viszont a felület növelésével nő. Ezért a legjobb dinamikája a kis felületű típusoknak van (kb. 50000:1). Az integráló típusú diszkrét elemekből álló (CCD) eszközök egy bizonyos korlátig (blooming) telítés esetén is alkalmasak pozíciómérésre. A PSD detektor azonban a működési elvéből következően csak a lineáris tartományban tud pozíciót mérni. Mivel a pozíciómérést a kifolyó áramok amplitúdó mérésére vezetjük vissza, ezért a nagy dinamika eléréséhez pontos jelfeldolgozás szükséges.
 +
 +
=====Sebesség=====
 +
Ezt a paramétert a PSD eszközöknél döntően a PIN dióda kapacitása határozza meg. A kapacitás csökkenthető záró irányú előfeszítéssel, de ekkor megnő a sötétáram. A nagyobb felületű típusok a nagyobb kapacitásuk miatt lassabbak. Tipikus felfutási idők  ($10\ k\Omega $-os munkaellenállásal) $2,5-50\ \mu s$. A diszkrét képpontokból álló eszközöknél valamennyi képpontot ki kell olvasni a következő mérés kezdetéig. A kiolvasás sebességét a CCD shift regiszterekkel elérhető max. 20 MHz-es órafrekvencia korlátozza a detektorsoroknál kb. $50-100\ \mu s$-ra, mátrixoknál néhány ms-ra. Ezen kívül a detektormátrixoknál a nagy mennyiségű adat gyors tárolása és feldolgozása is problémákat okoz.
 +
 +
Összefoglalva megállapíthatjuk, hogy a PSD analóg pozícióérzékelő detektorok számításba veendők, ha (1) nincs szükség a teljes intenzitáselosztásra, hanem elég csak egy folt koordinátáit, vagy az intenzitáselosztás megváltozását megmérni, (2) nagy sebességű mérés szükséges. Néhány tipikus alkalmazási terület:
 +
* valósidejű frekvencia analizátor akuszto-optikai Bragg cella használatával,
 +
* lézeres távolságmérő háromszögeléssel
 +
* ipari robotok mérőfejei
  
 
==Mérési feladatok==
 
==Mérési feladatok==
 +
1. Vegye föl a detektorok kimenő feszültség-detektált intenzitás (U<sub>ki</sub> - I) görbéjét (CCD: sor közepére beállított nyaláb, PSD: pl. függőleges középvonal mentén beállított nyaláb). Az intenzitás az optikai útba helyezett polarizátor forgatásával, illetve az intenzitáscsökkentő (ún. neutrál-) szűrők felhasználásával változtatható.
 +
 +
2. Határozza meg a detektorok dinamikáját a minimális és maximális detektálható intenzitás mérésével. Ha szükséges, használjon neutrál szűrőt a fényútban az intenzitás csökkentése érdekében.
 +
 +
3. Határozza meg a detektorok segítségével a fénynyaláb átmérőjét lencsével és lencse nélkül. Vegye figyelembe, hogy a CCD detektor véges szélességű tartományban integrál, valamint karakterisztikája logaritmikus! Gauss-nyalábot feltételezve vegye fel a tényleges nyalábokat és határozza meg annak félértékszélességét! Figyelem, a páros és páratlan csatornát egyaránt figyelembe kell venni!
 +
 +
4. Határozza meg a detektorok felbontását, valamint a PSD pozíció kimenőfeszültség karakterisztikáját (geometriai torzítását)!
  
 
==PDF formátum==
 
==PDF formátum==
 +
*[[Media:FÉLVEZETŐ FOTODETEKTOROK VIZSGÁLATA.pdf|Félvezető fotodetektorok vizsgálata (nem korrigált verzió)]]
  
 
</wlatex>
 
</wlatex>
 +
 +
<!--Utolso valtoztatas: 2013.09.25-->

A lap jelenlegi, 2013. szeptember 25., 14:46-kori változata


Tartalomjegyzék


Elméleti összefoglaló

Bevezetés

Manapság bármilyen berendezést, vagy készüléket tekintünk is, annak működtetése szinte elképzelhetetlen félvezető optikai detektorok nélkül. Gondoljunk csak a háztartási elektronika majd minden készülékébe beépített infravörös vevőegységre, a képfelvevő eszközökre, vagy akár a hőérzékelő elemekre hőfokmérő- és szabályzó egységekben, az ipari alkalmazásokról nem is beszélve. Az optikai detektorok skálája igen széles, érzékelési tartományuk a távoli infravöröstől az ultraibolyáig terjed. Azt mondhatnánk, hogy tulajdonképpen minden optikai sugárzást kibocsátó elemhez kifejlesztettek neki megfelelő detektort is.

Mivel az optikai detektorok felépítése, tulajdonságai, és egyéb paraméterei rendkívül sokoldalúak, egy hallgatói mérés során még felsorolásuk is lehetetlen. Ezért a mérés célja az, hogy ismeretet adjon egy-két, speciális tulajdonságokkal rendelkező detektortípusról. Ezek közelebbi vizsgálata megadja a módszert arra, hogyan kezdjük az ismerkedést immár tetszőleges típusú detektorral. Mielőtt a mérésben szereplő eszközök ismertetésére sor kerülne, szükséges néhány általánosan használt alapfogalom ismertetése.

Alapfogalmak

Minden anyag rendelkezik valamilyen - zérustól eltérő - belső energiával,- vagyis az őket felépítő atomok és molekulák mozgásban vannak. Mozgásuk során egymásra kölcsönhatnak (ütközések, kötések, stb. révén), így az atomok elemi töltéseinek gyorsulása van, miközben elektromágneses sugárzást bocsátanak ki.

Egy tökéletes sugárforrás - ún. feketetest - elektromágneses emisszióját a Planck-törvény írja le:

\[M_{e,\lambda } \left (\lambda, T\right ) {{=}} \frac{2\pi hc^2}{\lambda^5\left (e^{\frac{hc}{\lambda kT}}-1\right )}\]

ahol

  • \setbox0\hbox{$M_{e,\lambda}\left (\lambda, T\right ) \left [Wm^{-3} \right ]$}% \message{//depth:\the\dp0//}% \box0% a felületegység által kisugárzott spektrális sugárzási teljesítmény,
  • \setbox0\hbox{$\lambda [m]$}% \message{//depth:\the\dp0//}% \box0% az emittált hullámhossz,
  • \setbox0\hbox{$T[K]$}% \message{//depth:\the\dp0//}% \box0% az abszolút hőmérséklet,
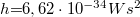  • \setbox0\hbox{$h {{=}} 6,62 \cdot 10^{-34} Ws^{2}$}% \message{//depth:\the\dp0//}% \box0% a Planck állandó,
  • \setbox0\hbox{$c[m/s]$}% \message{//depth:\the\dp0//}% \box0% a fénysebesség, és
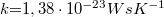  • \setbox0\hbox{$k {{=}} 1,38 \cdot 10^{-23} WsK^{-1}$}% \message{//depth:\the\dp0//}% \box0% a Boltzmann állandó.

A teljes hulllámhossz tartományon kisugárzott teljesítményt a Stefan-Boltzmann törvény adja:

\[M_e\left (T\right ) {{=}} \int\limits_0^\infty M_{e,\lambda} \left (\lambda ,T\right )d\lambda {{=}} \sigma_eT^4\]

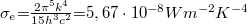
ahol \setbox0\hbox{$\sigma_e {{=}} \frac{2\pi^5k^4}{15h^3c^2} {{=}} 5,67 \cdot 10^{-8} Wm^{-2}K^{-4}$}% \message{//depth:\the\dp0//}% \box0%

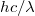A kisugárzott teljesítmény helyett a \setbox0\hbox{$\lambda$}% \message{//depth:\the\dp0//}% \box0% hullámhosszú foton (\setbox0\hbox{$hc/\lambda$}% \message{//depth:\the\dp0//}% \box0%) energiájának figyelembevételével megkaphatjuk az egységnyi felület teljes kisugárzott fotoáramát.

\[M_p\left (T\right ) {{=}} \int\limits_0^\infty M_{e,\lambda} \left (\lambda ,T\right )\frac{\lambda}{hc}d\lambda {{=}} \sigma_pT^3\]

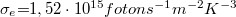ahol \setbox0\hbox{$\sigma_e {{=}} 1,52 \cdot 10^{15} fotons^{-1}m^{-2}K^{-3}$}% \message{//depth:\the\dp0//}% \box0%.

A Wien-féle eltolási törvény kapcsolatot teremt a hőmérséklet és a kisugárzott teljesítmény hullámhossz-szerinti maximuma között:

\[\lambda T\Big| _{\frac{\partial M_{e,\lambda}}{\partial \lambda} {{=}} 0} {{=}} 2898\ \mu mK\]

Egy valós anyag spektrális emisszióképességét az anyag által adott \setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0% térszögbe kisugárzott teljesítmény és a tökéletes fekete test által kisugárzott teljesítmény hányadosa adja:

\[\epsilon \left (\Omega,\lambda,T\right ) {{=}} \frac{L_{e,\lambda}(\lambda,T)_{anyag}}{L_{e,\lambda}(\lambda,T)_{fekete\ test}} {{=}} \epsilon_e(\lambda)\]

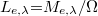ahol \setbox0\hbox{$L_{e,\lambda} {{=}} M_{e,\lambda}/\Omega$}% \message{//depth:\the\dp0//}% \box0%.

Megjegyzendő, hogy míg a spektrális fotonkibocsátás és az emisszióképesség minden esetben megegyezik,

\[\epsilon_e(\lambda) {{=}} \epsilon_p(\lambda)\]

az egész spektrumon integrált teljes emisszió általában nem azonos:

\[\epsilon_e {{=}}\frac{\int\limits_0^\infty\epsilon_e(\lambda)L_{e,\lambda}(\lambda,T)d\lambda}{\int\limits_0^\infty L_{e,\lambda}(\lambda,T)d\lambda} \neq \epsilon_p\]

Az elektromágneses sugárzás Kirchoff-törvénye szerint termikus egyensúlyban az emittált és abszorbeált energia megegyezik:

\[\alpha(\lambda) {{=}} \epsilon (\lambda)\]

Egy tetszőleges felületre beeső optikai nyaláb viselkedését három tényező írja le a következő módon:

\[\alpha + r + t {{=}} 1\]

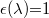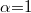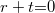ahol r és t a reflexió, illetve a transzmisszió. Tökéletes fekete test esetén \setbox0\hbox{$\epsilon(\lambda) {{=}} 1$}% \message{//depth:\the\dp0//}% \box0%, vagyis \setbox0\hbox{$\alpha {{=}} 1$}% \message{//depth:\the\dp0//}% \box0%, így \setbox0\hbox{$r+t {{=}} 0$}% \message{//depth:\the\dp0//}% \box0%.

Minden sugárforrás esetén fellép valamilyen bizonytalanság a kibocsátott elektromágneses sugárzás mennyiségében, melyet csak statisztikusan írhatunk le. n foton kibocsátásának valószínűségét a Poisson-eloszlás jól közelíti:

\[P_{\tau} (n) {{=}} \frac{n^{-n}}{n! \cdot e^{\overline{n}}} \qquad\overline{n} {{=}} \sum\limits_nP_{\tau}(n)n\]

ahol \setbox0\hbox{$\tau$}% \message{//depth:\the\dp0//}% \box0% a vizsgált időintervallum, és

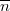\setbox0\hbox{$\overline{n}$}% \message{//depth:\the\dp0//}% \box0% a \setbox0\hbox{$\tau$}% \message{//depth:\the\dp0//}% \box0% idő alatt kibocsátott fotonok átlagos száma.

A detektált fotonok száma a kibocsátási folyamat diszkrét volta miatt binomiális eloszlást követ, mely nagyszámú megfigyelés esetén a Poisson-eloszláshoz közelít. A megfigyelő detektor m számú fotont érzékel, ha kvantumhatásfoka kisebb, mint egységnyi:

\[P_{\tau} (m) {{=}} \frac{{\left (\eta \overline{n}\right )}^{-n}}{m! \cdot e^{\eta\overline{n}}} \qquad\eta {{=}} \frac{\overline{m}}{\overline{n}}\]

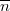ahol \setbox0\hbox{$\overline{n}$}% \message{//depth:\the\dp0//}% \box0% a detektorra érkező fotonok átlagos száma, és

\setbox0\hbox{$\eta$}% \message{//depth:\the\dp0//}% \box0% a detektor kvantumhatásfoka.

Az előzőekből következik, hogy egy tökéletesen zajmentes detektorral sem lehet végtelen jel/zaj viszonyt elérni. A sugárzás statisztikus volta meghatározza az elméletileg elérhető jel/zaj viszonyt:

\[SNR {{=}} \frac{\overline{n}}{\delta} {{=}} \sqrt{\overline{n}}\]

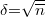ahol \setbox0\hbox{$\delta {{=}} \sqrt{\overline{n}}$}% \message{//depth:\the\dp0//}% \box0% a Poisson-eloszlás szórása. Nem egységnyi kvantumhatásfokú detektor esetén:

\[SNR {{=}} \frac{\eta\overline{n}}{\sqrt{\eta\overline{n}}} {{=}} \sqrt{\eta\overline{n}}\]

A detektor megfigyelt jel/zaj viszonya soha nem lehet jobb, mint az előző összefüggésben megadott érték.

Félvezető detektor működése

A fény kvantumos természetének következtében a fémek ionizációja akkor következik be, ha a foton 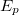\setbox0\hbox{$E_p$}% \message{//depth:\the\dp0//}% \box0% energiája meghaladja a fémben az elektron 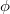\setbox0\hbox{$\phi$}% \message{//depth:\the\dp0//}% \box0% kilépési munkáját (fotoelektromos jelenség):

\[E_p {{=}} h\nu \geq \phi\]

A fotonok detektálhatóságát a fotonenergia és az anyag megengedett elektronenergia állapotainak kapcsolata határozza meg. Szilárdtestben az egyetlen atomra jellemző állapotok nagyszámú, egymáshoz közeli állapotokra - sávokra - hasadnak. Abszolút nulla fokon a legmagasabb betöltött energiaszintet 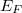\setbox0\hbox{$E_F$}% \message{//depth:\the\dp0//}% \box0% Fermi-szintnek nevezzük. A kilépési munka:

\[\phi {{=}} E_i - E_F\]

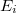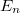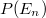ahol \setbox0\hbox{$E_i$}% \message{//depth:\the\dp0//}% \box0% az elektron ionizációs energiája. Magasabb hőmérsékleten a Fermi-szint megadja azt az energiaszintet, ahol a betöltési valószínűség 50%. Az egyes \setbox0\hbox{$E_n$}% \message{//depth:\the\dp0//}% \box0% energiaállapotok \setbox0\hbox{$P(E_n)$}% \message{//depth:\the\dp0//}% \box0% betöltési valószínűségét az elektronokra érvényes Fermi-Diac eloszlás adja:

\[P\left (E_n\right ) {{=}} \frac{1}{e^{\frac{E_n - E_f}{kT}}+1}\]

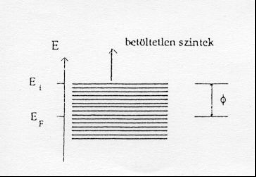
Az 1. ábra tünteti fel a fémekben az elektronok eloszlását, a legfelső betöltetlen energiasávban,

1. ábra Fémek elektroneloszlása
2. ábra Félvezetők megengedett állapotai

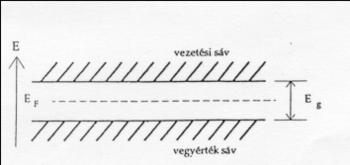
A szigetelők és a félvezetők sávszerkezete eltér a fémekétől, a vezetési (T = 0 K -en üres) és a vegyérték sáv egymástól elválik, közöttük széles tiltott sáv helyezkedik el. Az anyag mindaddig szigetelő, amíg a termikus energia kellően alacsony:

\[kT \ll E_g\]

Megjegyzendő, hogy a Fermi-szint közelítőleg a tiltott sáv felénél helyezkedik el. Termikus gerjesztés esetén az elektron a vezetési sávba kerül és egy pozitív töltésű lyukat hagy maga után, mely szintén hozzájárul az áramszállításhoz. Termikus egyensúly esetén az elektron és lyuk koncentráció megegyezik és az intrinsic (adalékolatlan) töltéshordozó-koncertráció az alábbi módon számolható:

\[n_i^2 {{=}} np {{=}}4\left ({\frac{2\pi \sqrt{m_n^*m_p^*}kT}{h^2}}^3\right )e^{-\frac{E_g}{kT}}\]

ahol ni, np intrinsic, elektron és lyuk töltéshordozó koncentráció,

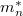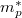\setbox0\hbox{$m_n^*$}% \message{//depth:\the\dp0//}% \box0%, \setbox0\hbox{$m_p^*$}% \message{//depth:\the\dp0//}% \box0% elektron és lyuk effektív tömeg.

A vezetés az alábbi módon adható meg pl. elektronokra:

\[\sigma {{=}} nq_e\mu_n\]

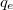ahol \setbox0\hbox{$q_e$}% \message{//depth:\the\dp0//}% \box0% az elektron töltése és 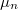\setbox0\hbox{$\mu_n$}% \message{//depth:\the\dp0//}% \box0% az elektronmozgékonyság:

\[\mu_n {{=}} \frac{\nu_d}{E_0} {{=}} \frac{q_e}{m_n^*}\overline{\tau}\]

amely arányos a töltéshordozók 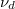\setbox0\hbox{$\nu_d$}% \message{//depth:\the\dp0//}% \box0% driftsebességének és az alkalmazott 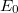\setbox0\hbox{$E_0$}% \message{//depth:\the\dp0//}% \box0% külső térerősségnek a hányadosával, illetve felírható az ütközések közötti 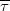\setbox0\hbox{$\overline{\tau}$}% \message{//depth:\the\dp0//}% \box0% átlagos idő és az effektív tömeg segítségével.

Termikus gerjesztés mellett más, (pl. foton-} gerjesztésre is kerülhet töltéshordozó a vezetési sávba, ha a foton energiája:

\[h\nu \geq E_g\]

A leggyakoribb optikai detektálási mód, hogy mérjük az eszköz vezetőképességét (vagy ellenállását: fotokonduktív detektorok).

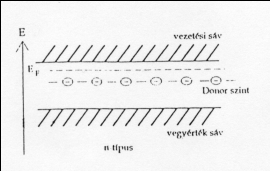
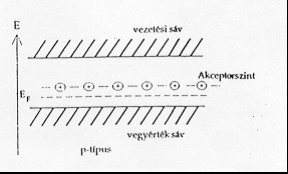
Az extrinsic ("külső vezetésű") félvezetők a kristályrácsba beépített adalékatomok hatása következtében válnak vezetővé. Az adalékatomok donorok, ha negatív töltésfelesleget visznek be a kristályba, akceptorok, ha pozitívat. A 3. és 4. ábra mutatja az adalékolt félvezetők sávszerkezetét.

3. ábra A donorok hatása a sávszerkezetre
4. ábra Az akceptorok hatása a sávszerkezetre

Az ábrák illusztrálják a Fermi-nívó eltolódást is. Megfelelő adalékolás esetén a félvezető vezetési tulajdonságai nagymértékben függetlenné válnak a hőmérséklettől, mivel így a vezetést nem a termikusan gerjesztett, hanem az adalékolás hatására a tiltott sáv szélességénél jóval kisebb energiával a vezetési sávba gerjesztett donor elektronok, illetve az akceptor szintek gerjesztettsége miatt a vegyértéksávban létrehozott lyukak biztosítják.

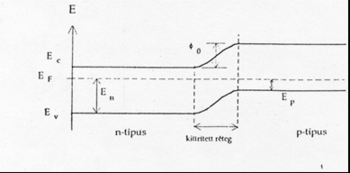
Ha p-n átmenetet hozunk létre különböző vezetési típusú félvezetőkből, az egyensúly beállításához szükséges a Fermi-szintek kiegyenlítődése, ahogy az az 5. ábrán látható. Ez potenciálkülönbséget hoz létre a p-n átmeneten, melynek egyensúlyi értéke:

\[\phi_0 \approx \frac{kT}{q_e}ln\frac{n_pp_n}{n_i^2}\]

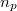ahol \setbox0\hbox{$n_p$}% \message{//depth:\the\dp0//}% \box0% az elektronkoncentráció a p-tartományban és

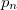\setbox0\hbox{$p_n$}% \message{//depth:\the\dp0//}% \box0% a lyukkoncentráció az n-tartományban melyeket kisebbségi töltéshordozónak nevezünk.

A kisebbségi töltéshordozók jelenlétét azok ellentétes tartományból történő diffúziója okozza. A diffúzió következtében a p-n átmenet közelében a töltéshordozó-koncentráció csökken, vagyis kiürített tartomány jön létre, mely a - pozitív, illetve negatív atomtörzsek révén biztosítja a Fermi-nívó kiegyenlítéséhez szükséges 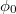\setbox0\hbox{$\phi_0$}% \message{//depth:\the\dp0//}% \box0% potenciálkülönbséget.

5. ábra A p-n átmenet

Külső nyitófeszültség hatására (n-oldalra negatív, p-oldalra pozitív feszültséget kapcsolva), a kiürített réteg szélessége, így 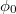\setbox0\hbox{$\phi_0$}% \message{//depth:\the\dp0//}% \box0% értéke csökken, az átmeneten áthaladó áram pedig exponenciális függvény szerint növekszik. Fordított irányú - zárófeszültség esetén 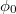\setbox0\hbox{$\phi_0$}% \message{//depth:\the\dp0//}% \box0% , értéke növekszik, az áram pedig csökken. Ebben az esetben jelentőssé válik a - kisebbségi töltéshordozók által szállított - zéróirányú, ún. visszáram. Külső, pl. fotongerjesztéssel a visszáram értéke jelentősen nő, a gerjesztés révén keletkező kisebbségi töltéshordozó-párok miatt. Ezen az elven működnek az ún. fotovoltaikus detektorok.

Érdemes megjegyezni, hogy a félvezető eszközökben az áramot kétféle hatás alakítja ki, melyekkel a teljes j áramsűrűség elektronokra és lyukakra (vektoriális formában):

\[j_n {{=}} +q_eD_ngradn + q_en\mu_nE\]
\[j_p {{=}} -q_eD_ngradp + q_en\mu_pE\]

Az egyenletek első tagja a töltéshordozó-koncentráció eltérésből eredő gradiens okozta diffúziót írja le. A D diffúziós állandó kifejezése az ún. Einstein-összefüggéssel lehetséges:

\[D_{n,p} {{=}} \frac{kT}{q_e}\mu_{n,p}\]

Az áramsűrűség másik összetevője a külső E térerősség hatására létrejövő ún. drift, mely a vezetőképességgel kifejezve:

\[j_{n,p,E} {{=}} \sigma_{n,p}E\]

Detektálási mechanizmusok

A két alapvető detektálási mód a fotokonduktív és a fotovoltaikus, mindkettő a belső fotoeffektuson alapul.

A fotokonduktív detektor elektronjai megfelelő energiájú foton hatására gerjesztődnek, vagyis nő a vezetésben résztvevő töltéshordozók koncentrációja, így az eszköz vezetőképessége változik:

\[\Delta \sigma {{=}} \Delta nq_e\mu_n\]

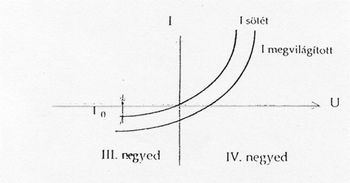
Fotovoltaikus esetben a beérkező fotonok hatására a p-n átmenetben töltéshordozó párok keletkeznek, és az elektronok a p-rétegből az n-rétegbe, a lyukak az n-ből a p-rétegbe vándorolnak, a kiürített réteg által létrehozott elektromos tér hatására. Ennek következtében megváltozik a p-n átmenet feszültség-áram karakterisztikája a 6.ábrának megfelelően.

A fotovoltaikus detektor I-U görbéje 6. ábra

A görbe alapján a detektor működhet záróirányban előfeszítve (III. síknegyed), vagy rövidzárban (IV. síknegyed), pl, műveleti erősítő bemenetére kapcsokra, mert így a fotoáram a fotonfluxus lineáris függvénye, hiszen a detektordinamikus ellenállása ekkor állandó hőmérsékleten állandó:

\[R_d {{=}} \frac{\partial U}{\partial I}\bigg \vert_{U=0} {{=}} \frac{\beta kT}{q_eI_0}e^{-\frac{q_eU}{\beta kT}}\bigg \vert_{U=0} {{=}}\ \acute{a}lland\acute{o}\]

A harmadik típusú detektor a fotoemissziós elvet alkalmazza, vagyis működése ~a fotoelelektromos hatáson (direkt fotoeffektus) alapul. Ebben az esetben az alacsony kiléoési munkájú ún. fotokatódból kilépő elektron biztosítja a fotoáramot (pl. fotoelektronsokszorozó fotokatódja). E három típuson kívül még sokféle működési mechanizmus létezik, melyeken hely hiányában nem tárgyalunk (bolométerek, piezoelektromos detektorok, stb.).

A detektorok jellemzői

A következőkben definiált mennyiségek (spektrális érzékenység, NEP, SNR és detektivitás) az egyes detektorok paramétereinek összehasonlítására szolgálnak adott feladat esetén. Feladattól függően igen sokféle jellemző mennyiség definálható, itt csak a legfontosabbakat említjük meg.

Spektrális érzékenység: a detektor kimenő jelének és a beeső sugárzási teljesítménynek a hányadosa:

\[\Re_u (\lambda ) {{=}} \frac{u_{ki}}{\phi_e (\lambda )} \qquad vagy \qquad \Re_i (\lambda ) {{=}} \frac{i_{ki}}{\phi_e(\lambda )}\]

ahol uki[V], a detektor kimeneti jelfeszültsége,

vagy iki[A] , kimeneti jeláram,

és \setbox0\hbox{$\phi_e(\lambda[W])$}% \message{//depth:\the\dp0//}% \box0%, a beeső spektrális fényteljesítmény.

NEP: zaj egyenértékű teljesítmény (noise equivalent power), dimenziója [W] az a legkisebb fényteljesítmény, amely egységnyi jel/zaj viszonyt produkál.

Ekkor a kimenő jel (pl. iki ) nagysága megegyezik a kimenő zaj "rms" (négyzetes közép-} értékével:

\[SNR {{=}} \frac{i_{ki}}{i_{rms}} {{=}} \frac{\Re_i\phi_c}{i_{rms}} \qquad SNR {{=}} 1 {{=}} \frac{\Re_iNEP}{i_{rms}}\]

Detektivitás:

\[D {{=}} \frac{1}{NEP}[W^{-1}]\]

Jel/zaj viszony (SNR - signal-to-noise ratio): a kimenő jel és az "rms" zaj hányadosa. Az SNR értéke mindig kisebb, mint a zajmentes detektorra a 2. részben definiált SNR.

A detektorzaj forrásai a következők:

  • Foton-zaj (a sugárzási zaj)
  • Detektor által generált zaj (Johnson-, 1/f-, hőmérsékleti-, stb.)
  • Áramköri zaj (hasonlóan a b. ponthoz)

Képérzékelő eszközök

A képérzékelő eszközök a fotodetektorok általánosításának is tekinthetők annyiban, hogy a kimenő jel nemcsak a felületet ért átlagos megvilágításról, hanem annak térbeli eloszlásáról is ad információt. Így a képérzékelő eszközök is - az egyszerű detektorokhoz hasonlóan - csoportosíthatók a fény-anyag kölcsönhatás (a detektálás mechanizmusa} szerint. Egy másik csoportosítás szerint a fotodetektorok integráló és nem integráló típusú eszközökre oszthatók. Ebben az esetben, bár a detektálási mechanizmusok ugyanazok, a kimenő jel információtartalma eltérő az egyes eszközökben. Ennek különösen impulzus, vagy egyéb, időben változó fényintenzitás-eloszlások detektálásakor van jelentősége. A mérés során kétféle detektorral ismerkedünk meg, egy integráló típusú ún. CCD detektorsorral és egy nem integráló típusú ún. analóg pozícióérzékelő detektormátrixszal.

Lineáris (CCD) detektorsorok

A jelfeldolgozó és képfelvevő eszközök területén a töltéscsatolt eszközök (CCD - charge coupled device) megalkotása nyitott új perspektívát az 1970-es évek elején. Működésük alapja, hely periódikus fém-szigetelő-félvezető (MIS - metal-insulator-semiconductor) struktúrában lehetőség van töltéscsomagok létrehozására. A töltéstárolás mechanizmusát a MIS kapacitás modell alapján, a töltéstovábbítást pedig a szabad elektron modell alapján lehet tárgyalni. A megvalósított eszközökben a detektorelemek térben mindig elkülönülnek a kiolvasó shift regiszterektől.

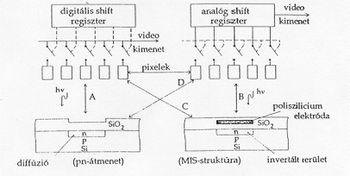
A 7. ábra a lineáris szilárdtest képérzékelők négy alapvető fajtáját szemlélteti. A felső sorban a két alapvető kiolvasási mód (digitális shift regiszterrel vezérelt analóg kapcsolók, ill. analóg CCD shift regiszter), az alsó sorban pedig a két alapvető érzékelő elemtípus (diffúzióval előállított fotodióda, ill. MOS kapacitás) metszete látható- Az ábrán A, B, C és D betűvel jelöltük a kétféle kiolvasási mód és a kétféle ~detektortípus lehetséges négy kombinációját

A lineáris detektorsorok fajtái 7. ábra

Az „A" esetben diffúzióval előállított p-n átmenetet tartalmazó fotodióda a detektor. Digitális shift regiszter kapcsolja egymás után a kimenetre a detektorokat. Ez az elrendezés az ún. "self-scanned" fotodiódasor (SSPD). A "B" elrendezésben (CCD detektorsor) a töltések a poliszilícium elektróda alatt létrejövő inverziós rétegben képződnek, amit pixelnek (elemi képpontnak) hívnak. A pixelekből az információ átírása párhuzamosan történik egy analóg shift regiszterbe, amelynek a kimenetén a soros videojel jelenik meg. A "C" és "D" elrendezés a kétféle detektor és a kétféle kiolvasási mód további kombinációja. A "D" típus az ún. CCPD (töltéscsatolt fotodióda). 1987-ben fejlesztettek ki egy új típusú, ún. FOTOFET érzékelő elemekből felépített különlegesen nagy dinamikájú detektorsor családot. (Detektordinamikán a maximálisan megengedhető és a minimálisan detektálható optikai jel arányát értjeük. A FOTOFET a Dalsa cég szabadalma, felépítését tekintve egy hagyományos p-n átmenetes és n-csatornás MOS struktúrájú fotodióda kombinációja, míg a töltéskiolvasás módja a CCD detektorsorban alkalmazotthoz áll a legközelebb.

A mérésben használt detektorsor is egy Dalsa cég által gyártott - igen nagy dinamikatartománnyal rendelkező (névlegesen 106:1) - típus. Ennek ára viszont, hogy az eszköz karakterisztikája nem lineáris a teljes tartományban, hanem nagy intenzitásoknál logaritmikus. Ennek következtében viszont nem lép fel az ún. blooming (foltkiszélesedési) jelenség. (Nagy intenzitásoknál ugyanis a töltések távolabbi pixeleken is megjelennek - töltésszétfolyás -, így az egész detektorsor telítésbe kerülhet!) A sor 2048 elemi képpontot tartalmaz, melyek távolsága és szélessége is 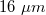\setbox0\hbox{$16\ \mu m$}% \message{//depth:\the\dp0//}% \box0%. A páros és páratlan képpontok kiolvasására egy-egy analóg shift regisztereket tartalmazó csatorna áll rendelkezésre.

Az analóg pozícióérzékelő detektor (PSD)

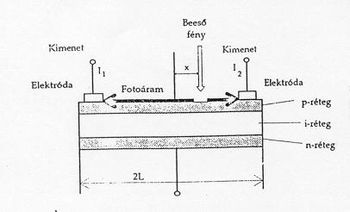
Az analóg pozícióérzékelő detektorok (PSD) kb. 1984-ben jelentek meg először. Ezek nem valódi képérzékelő eszközök, mivel csak a rájuk eső intenzitáseloszlás súlypontjának koordinátáját képesek megmérni. A PSD eszköz három rétegből áll (8. ábra): p-, n-, és i-típusúból. Ezeket a rétegeket egy Si szeleten hozzák létre. Ha a felületre fényfolt esik, az időegység alatta fényteljesítménnyel arányos mennyiségű töltéshordozót generál a beesés helyén. A töltések a p-típusú ellenállásrétegen keresztül haladnak az elektródák felé. Mivel a p-réteg ellenállása egyenletes, az elektródákon kifolyó áram fordítottan arányos a beesési pont és az elektróda közt mérhető távolsággal.

Ha a két elektróda távolsága 2L, a kifolyó teljes áram , akkor a középponttól mért pozíciót a következő összefüggésekkel kaphatjuk meg:

\[I_1 {{=}} I_0\cdot\frac{L - x}{2L} \qquad I_2 {{=}} I_0\cdot\frac{L + x}{2L} \qquad \frac{I_2 - I_1}{I_2 + I_1} {{=}} \frac{x}{L}\]
Az analóg pozícióérzékelő detektor (PSD) 8. ábra

A fenti összefüggések igazak tetszőleges intenzitáseloszlás eredő súlypontjának meghatározásánál is. A PSD eszközök (lehetnek egy- vagy kétdimenziósak is. A torzítás csökkentésére és a felbontóképesség javítására a kétdimenziós eszközöknek javított változatai is lehetnek, de valamennyinél azonos a működés alapelve.

A PSD és CCD detektorok paramétereinek összehasonlítása

Spektrális érzékenység

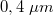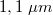A PSD eszközök spektrális érzékenysége - a Si-ból készült szilárdtest képérzékelő eszközökhöz hasonlóan - kb. \setbox0\hbox{$0,4\ \mu m$}% \message{//depth:\the\dp0//}% \box0%-től \setbox0\hbox{$1,1\ \mu m$}% \message{//depth:\the\dp0//}% \box0%-ig terjed, tehát pl. 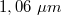\setbox0\hbox{$1,06\ \mu m$}% \message{//depth:\the\dp0//}% \box0% hullámhosszú Nd-YAG lézer fényt még jól detektálják.

Felbontás

Ezt a paramétert általában a fényfolt legkisebb detektálható elmozdulásával definiálják. Az irodalom szerint a felbontás független a foltmérettől és arányos a detektort ért megvilágítással. Mivel a PSD eszközökben a pozíciót amplitúdóméréssel lehet meghatározni, a felbontást jelentősen befolyásolja a detektorhoz kapcsolódó elektronikus rendszer zaja is. A katalógusok ezért mindig megadják a mérési körülményeket is, pl.:

  • fényforrás: LED (900 nm),
  • fényfolt mérete: 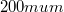\setbox0\hbox{$200\\mu m$}% \message{//depth:\the\dp0//}% \box0% átmérő,
  • frekvencia: 10 kHz,
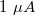  • fotoáram: \setbox0\hbox{$1\ \mu A$}% \message{//depth:\the\dp0//}% \box0%,
  • elektronika bemenő zaja: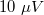\setbox0\hbox{$10\ \mu V$}% \message{//depth:\the\dp0//}% \box0% (sávszélesség 10 kHz).

Ilyen feltételek mellett típustól függően egy irányban 1000-10000 diszkrét pontnak megfelelő felbontás mérhető.

PSD detektorok tipikus torzítása (A vonalak közötti valós távolság konstans) 9. ábra

Itt kell megemlíteni a kétdimenziós PSD eszközök egy jelentős hátrányát a detektormátrixokkal szemben. Ez a paraméter a geometriai torzítás. A diszkrét érzékelőjü szilárdtest eszközöknek gyakorlatilag nincs geometriai torzítása, mivel a gyártástechnológia igen pontos mérettartást tesz lehetővé a teljes felületen. A kétdimenziós PSD eszközök esetében a szélek felé haladva már nem lineáris az összefüggés a fényfolt tényleges elmozdulása és az áramokból meghatározott érték között. A 9. ábrán látható egy tipikus mért torzítási görbesereg, amelynek segítségével a mérőkészüléket kalibrálni kell. Az újabb fejlesztésű - korrigált geometriával rendelkező - eszközök torzítása lényegesen kisebb.

Dinamika

A PSD eszközök lineáris tartományát felülről a maximális fotoáram korlátozza, alulról pedig a sötétáram. A maximális fotoáram minden típusnál ugyanaz (kb. 1 mA), a sötétáram viszont a felület növelésével nő. Ezért a legjobb dinamikája a kis felületű típusoknak van (kb. 50000:1). Az integráló típusú diszkrét elemekből álló (CCD) eszközök egy bizonyos korlátig (blooming) telítés esetén is alkalmasak pozíciómérésre. A PSD detektor azonban a működési elvéből következően csak a lineáris tartományban tud pozíciót mérni. Mivel a pozíciómérést a kifolyó áramok amplitúdó mérésére vezetjük vissza, ezért a nagy dinamika eléréséhez pontos jelfeldolgozás szükséges.

Sebesség

Ezt a paramétert a PSD eszközöknél döntően a PIN dióda kapacitása határozza meg. A kapacitás csökkenthető záró irányú előfeszítéssel, de ekkor megnő a sötétáram. A nagyobb felületű típusok a nagyobb kapacitásuk miatt lassabbak. Tipikus felfutási idők (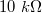\setbox0\hbox{$10\ k\Omega $}% \message{//depth:\the\dp0//}% \box0%-os munkaellenállásal) 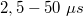\setbox0\hbox{$2,5-50\ \mu s$}% \message{//depth:\the\dp0//}% \box0%. A diszkrét képpontokból álló eszközöknél valamennyi képpontot ki kell olvasni a következő mérés kezdetéig. A kiolvasás sebességét a CCD shift regiszterekkel elérhető max. 20 MHz-es órafrekvencia korlátozza a detektorsoroknál kb. 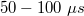\setbox0\hbox{$50-100\ \mu s$}% \message{//depth:\the\dp0//}% \box0%-ra, mátrixoknál néhány ms-ra. Ezen kívül a detektormátrixoknál a nagy mennyiségű adat gyors tárolása és feldolgozása is problémákat okoz.

Összefoglalva megállapíthatjuk, hogy a PSD analóg pozícióérzékelő detektorok számításba veendők, ha (1) nincs szükség a teljes intenzitáselosztásra, hanem elég csak egy folt koordinátáit, vagy az intenzitáselosztás megváltozását megmérni, (2) nagy sebességű mérés szükséges. Néhány tipikus alkalmazási terület:

  • valósidejű frekvencia analizátor akuszto-optikai Bragg cella használatával,
  • lézeres távolságmérő háromszögeléssel
  • ipari robotok mérőfejei

Mérési feladatok

1. Vegye föl a detektorok kimenő feszültség-detektált intenzitás (Uki - I) görbéjét (CCD: sor közepére beállított nyaláb, PSD: pl. függőleges középvonal mentén beállított nyaláb). Az intenzitás az optikai útba helyezett polarizátor forgatásával, illetve az intenzitáscsökkentő (ún. neutrál-) szűrők felhasználásával változtatható.

2. Határozza meg a detektorok dinamikáját a minimális és maximális detektálható intenzitás mérésével. Ha szükséges, használjon neutrál szűrőt a fényútban az intenzitás csökkentése érdekében.

3. Határozza meg a detektorok segítségével a fénynyaláb átmérőjét lencsével és lencse nélkül. Vegye figyelembe, hogy a CCD detektor véges szélességű tartományban integrál, valamint karakterisztikája logaritmikus! Gauss-nyalábot feltételezve vegye fel a tényleges nyalábokat és határozza meg annak félértékszélességét! Figyelem, a páros és páratlan csatornát egyaránt figyelembe kell venni!

4. Határozza meg a detektorok felbontását, valamint a PSD pozíció kimenőfeszültség karakterisztikáját (geometriai torzítását)!

PDF formátum



A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Félvezető_fotodetektorok&oldid=12905”