„Kis fényintenzitások mérése zajos környezetben: Mérések spektrofotométerrel, hidrogén színkép vizsgálata” változatai közötti eltérés
Lenk (vitalap | szerkesztései) a |
Lenk (vitalap | szerkesztései) a |
||
| (egy szerkesztő 12 közbeeső változata nincs mutatva) | |||
| 51. sor: | 51. sor: | ||
Ebből ([[#eq:1|1]]) alapján kifejezhető a kisugárzott foton hullámszáma: | Ebből ([[#eq:1|1]]) alapján kifejezhető a kisugárzott foton hullámszáma: | ||
| − | {{eq|\overline\nu {{=}} \frac{\Delta E}{c\cdot h} {{=}} \frac{m\cdot e^4}{8\cdot c\cdot\epsilon_0^2 \cdot h^3} \cdot \left( \frac{1}{n_0^2} - \frac{1}{n_1^2}\right) {{=}} R_{\infty} \cdot \left(\frac{1}{n_0^2} - \frac{1}{n_1^2}\right) \Rightarrow \frac{1}{\lambda} {{=}} \left(\frac{1}{n_0^2} - \frac{1}{n_1^2}\right)|eq:5|(5)}} | + | {{eq|\overline\nu {{=}} \frac{\Delta E}{c\cdot h} {{=}} \frac{m\cdot e^4}{8\cdot c\cdot\epsilon_0^2 \cdot h^3} \cdot \left( \frac{1}{n_0^2} - \frac{1}{n_1^2}\right) {{=}} R_{\infty} \cdot \left(\frac{1}{n_0^2} - \frac{1}{n_1^2}\right) \Rightarrow \frac{1}{\lambda} {{=}} R_{\infty} \cdot \left(\frac{1}{n_0^2} - \frac{1}{n_1^2}\right)|eq:5|(5)}} |
| − | ahol $R_{\infty}$ a Rydberg-állandó. A jelölésben alkalmazott „∞” szimbólum azt jelenti, hogy az energia ([[#eq:3|3]]) képletének levezetésénél az atommag tömegét végtelen nagynak tekintettük az elektronéhoz képest. Az elhanyagolás miatt hidrogén esetében $R_{\infty}$-től csekély eltérést tapasztalunk. A kis korrekció miatt a hidrogén atom Rydberg-állandója: | + | ahol $R_{\infty}$ a Rydberg-állandó. A jelölésben alkalmazott „∞” szimbólum azt jelenti, hogy az energia ([[#eq:3|3]]) képletének levezetésénél az atommag tömegét végtelen nagynak tekintettük az elektronéhoz képest. Az elhanyagolás miatt hidrogén esetében $R_{\infty}$-től csekély eltérést tapasztalunk. A kis korrekció miatt a hidrogén atom Rydberg-állandója: $R_H \sim 1,0968 \cdot 10^7 \frac{1}{m} $ . Az alapállapot főkvantum-számának (n<sub>0</sub>) rögzítésével emissziós sorozatokat kapunk, melyek közül az n<sub>0</sub> = 2 (az ún. Balmer-sorozat) adja a hidrogén látható színképét. A Balmer-sorozat első négy tagja (n<sub>1</sub> = 3, 4, 5, 6) esik az emberi szemmel látható fény tartományába (ezeket H<sub>α</sub>, H<sub>β</sub>, H<sub>γ</sub>, H<sub>δ</sub>-val jelölik). Ez a spektrum, valamint egy hidrogén lámpa képe látható a [[#fig:2a|2. ábrán]]. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| {{fig|hidrogén_lámpa.jpg|fig:2a|2. a. ábra hidrogén lámpa}} | | {{fig|hidrogén_lámpa.jpg|fig:2a|2. a. ábra hidrogén lámpa}} | ||
| − | {{fig|spektométer_belépő_rése.jpg|fig:2b|2. b. ábra spektométer belépő rése}} | + | | {{fig|spektométer_belépő_rése.jpg|fig:2b|2. b. ábra spektométer belépő rése}} |
{{fig|belépő_rés_képe_a_monokromátor_képsíkjában.jpg|fig:2c|2. c. ábra belépő rés képe a monokromátor képsíkjában. A hidrogén látható színképének négy atomi vonala közötti folytonos háttér a gerjesztett hidrogén molekuláktól és ionoktól származik.}} | {{fig|belépő_rés_képe_a_monokromátor_képsíkjában.jpg|fig:2c|2. c. ábra belépő rés képe a monokromátor képsíkjában. A hidrogén látható színképének négy atomi vonala közötti folytonos háttér a gerjesztett hidrogén molekuláktól és ionoktól származik.}} | ||
|} | |} | ||
| 75. sor: | 75. sor: | ||
{{eq|k\cdot\lambda {{=}} \frac{2}{G}\cdot\sin(\theta)+x\cdot\frac{\cos(\theta)}{f\cdot G} \left[mm\right]|eq:6|(6)}} | {{eq|k\cdot\lambda {{=}} \frac{2}{G}\cdot\sin(\theta)+x\cdot\frac{\cos(\theta)}{f\cdot G} \left[mm\right]|eq:6|(6)}} | ||
| − | ahol $\theta$ a kijelzett szögállás, „k” a diffrakció rendje (mérésünkben k = 1), f = 2075 mm (a PGS-2 homorútükrének fókusztávolsága), és G = 651,5 | + | ahol $\theta$ a kijelzett szögállás, „k” a diffrakció rendje (mérésünkben k = 1), f = 2075 mm (a PGS-2 homorútükrének fókusztávolsága), és G = 651,5 mm<sup>−1</sup> (a PGS-2 diffrakciós rácsának térfkervenciája, azaz a milliméteren-kénti osztásszám.) Az „x” a spektrométer kilépő résének pozíciója [mm]-ben. Jelen esetben értéke bizonytalan: x = −2..+2 mm, ami a mérést hibával terheli. |
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
| 96. sor: | 96. sor: | ||
A léptetés végén mentse el az adatokat („Save As...”), és ellenőrizze, hogy a számítógép által lejegyzett szögérték megegyezik-e a valóságossal! Mekkora eltérést tapasztal? Becsülje meg ez mekkora eltérést eredményezhet hullámhosszban! A rések 0,1 mm-es szélessége hány nm-nek felel meg ebben a spektrométerben? A mért H<sub>α</sub>, H<sub>β</sub>, H<sub>γ</sub>, H<sub>δ</sub> hullámhossz-szögérték adatok alapján ([[#eq:6|6]]) segítségével határozza meg az „x” paramétert! (Pl. mind a négy hullámhosszra kiszámítani x-et, majd átlagolni.) | A léptetés végén mentse el az adatokat („Save As...”), és ellenőrizze, hogy a számítógép által lejegyzett szögérték megegyezik-e a valóságossal! Mekkora eltérést tapasztal? Becsülje meg ez mekkora eltérést eredményezhet hullámhosszban! A rések 0,1 mm-es szélessége hány nm-nek felel meg ebben a spektrométerben? A mért H<sub>α</sub>, H<sub>β</sub>, H<sub>γ</sub>, H<sub>δ</sub> hullámhossz-szögérték adatok alapján ([[#eq:6|6]]) segítségével határozza meg az „x” paramétert! (Pl. mind a négy hullámhosszra kiszámítani x-et, majd átlagolni.) | ||
| − | |||
| + | ===2. feladat: LED spektrumának meghatározása=== | ||
Tegye a fény emittáló diódát (LED) egész közel a belépő réshez. FIGYELEM: a mérésvezérlő szoftver 0-10 V méréstartományban működik, ennek megfelelően kell a fényforrást elhelyezni a rés előtt (túl sok fény esetén távolítani, kevés esetén közelíteni kell a LED-et). A tápegységen állítson be áramkorlátnak 20 mA-t, feszültségkorlátnak 3,5 V-ot. Csatlakoztassa a diódát a tápegységhez (a hosszabb lábat a pozitív pólushoz). Milyen színű fényt bocsát ki a dióda? Ennek megfelelő hullámhossztartományt rögzítsen a számítógép segítségével, ehhez használja a normálás funkciót! FIGYELEM: technikai okokból a detektor érzékenységét 370-840 nm hullámhossz tartományban kalibráltuk, a kalibráció hibája kb. ±3%. Vizsgálja meg hogyan változik a spektrum, ha 10 mA-re lecsökkenti a diódaáramot! Az átállításhoz az on/off gombbal vegye le a feszültséget! Mindkét spektrumot mentse el, és az előző pontban kiszámított x-et behelyettesítve ábrázolja azokat! | Tegye a fény emittáló diódát (LED) egész közel a belépő réshez. FIGYELEM: a mérésvezérlő szoftver 0-10 V méréstartományban működik, ennek megfelelően kell a fényforrást elhelyezni a rés előtt (túl sok fény esetén távolítani, kevés esetén közelíteni kell a LED-et). A tápegységen állítson be áramkorlátnak 20 mA-t, feszültségkorlátnak 3,5 V-ot. Csatlakoztassa a diódát a tápegységhez (a hosszabb lábat a pozitív pólushoz). Milyen színű fényt bocsát ki a dióda? Ennek megfelelő hullámhossztartományt rögzítsen a számítógép segítségével, ehhez használja a normálás funkciót! FIGYELEM: technikai okokból a detektor érzékenységét 370-840 nm hullámhossz tartományban kalibráltuk, a kalibráció hibája kb. ±3%. Vizsgálja meg hogyan változik a spektrum, ha 10 mA-re lecsökkenti a diódaáramot! Az átállításhoz az on/off gombbal vegye le a feszültséget! Mindkét spektrumot mentse el, és az előző pontban kiszámított x-et behelyettesítve ábrázolja azokat! | ||
| 103. sor: | 103. sor: | ||
A fizikából tanultak alapján diffrakciós rácsok esetében a beeső fénysugár felületnormálissal bezárt szöge (α−θ), és a „k”-ik rendbe diffraktált fénysugár felületnormálissal bezárt szöge (β+θ) között az álábbi összefüggés áll fönn (magyarázat ld. a [[#fig:6|6.a. ábrán]]): | A fizikából tanultak alapján diffrakciós rácsok esetében a beeső fénysugár felületnormálissal bezárt szöge (α−θ), és a „k”-ik rendbe diffraktált fénysugár felületnormálissal bezárt szöge (β+θ) között az álábbi összefüggés áll fönn (magyarázat ld. a [[#fig:6|6.a. ábrán]]): | ||
| − | {{eq|\sin(\beta+\theta) - \sin(\alpha-\theta){{=}} k\cdot G \cdot \lambda|eq:7|(7)}} | + | {{eq|\sin(\beta+\theta) - \sin(\alpha-\theta){{=}} k\cdot G \cdot \lambda \qquad (G {{=}} \frac{1}{d},\ d\ a\ r\acute{a}cs\acute{a}lland\acute{o})|eq:7|(7)}} |
ahol „G” a rács rovátkáinak térfrekvenciája, α a beeső fénysugár és β a diffraktált fénysugár z-tengellyel (azaz a homorú főtökör forgástengelyével) bezárt szög (figyelem: β és θ előjeles szögek!). A fenti egyenlet trigonometrikus azonosságok alapján így írható át: | ahol „G” a rács rovátkáinak térfrekvenciája, α a beeső fénysugár és β a diffraktált fénysugár z-tengellyel (azaz a homorú főtökör forgástengelyével) bezárt szög (figyelem: β és θ előjeles szögek!). A fenti egyenlet trigonometrikus azonosságok alapján így írható át: | ||
| 123. sor: | 123. sor: | ||
A PGS-2 spektrométer monokromátorának esetében α ≈ 0 és x << f. Ezekkel a közelítésekkel ([[#eq:11|11]]) jelentősen leegyszerűsödik: | A PGS-2 spektrométer monokromátorának esetében α ≈ 0 és x << f. Ezekkel a közelítésekkel ([[#eq:11|11]]) jelentősen leegyszerűsödik: | ||
| − | {{eq|k \cdot G \cdot \lambda {{=}} \sin(\theta) \cdot 2 + x \cdot \frac{\cos(\theta)}{f}|eq:12|(12)}} | + | {{eq|k \cdot G \cdot \lambda {{=}} \sin(\theta) \cdot 2 + x \cdot \frac{\cos(\theta)}{f} \Rightarrow k\cdot \lambda {{=}} \frac{2}{G}\cdot\sin(\theta) + x\cdot \frac{\cos(\theta)}{f \cdot G}|eq:12|(12)}} |
| + | |||
| + | amivel megkaptuk a keresett ([[#eq:6|6]]) egyenletet, amely előjelhelyesen írja le x és θ kapcsolatát. | ||
| − | |||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
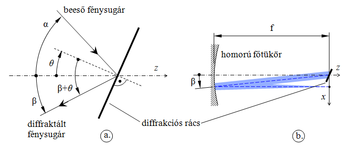
| − | | {{fig| | + | | {{fig|Szinkep6.png|fig:6|6. ábra. Magyarázat a monokromátor egyenletének levezetéséhez. a. diffraktált fénysugár irányának meghatározása. b. a diffraktált fénynyaláb fókuszpontja x-koordinátájának meghatározása.}} |
|} | |} | ||
| − | |||
==PDF formátum== | ==PDF formátum== | ||
| − | + | *[[Media:kisfeny_hidrogenL.pdf|Mérések spektrofotométerrel, hidrogén színkép vizsgálata]] | |
| − | *[[Media: | + | |
</wlatex> | </wlatex> | ||
| + | <!--Utolso szerkesztes:2013.09.25--> | ||
A lap jelenlegi, 2013. szeptember 27., 10:19-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Bevezetés
Már régóta ismert jelenség, hogy különféle anyagokat magas hőmérsékletű lángba helyezve a láng színében az adott anyagra jellemző elváltozás tapasztalható. Hasonló jelenség lép fel akkor is, ha kisülési csőbe az azt létrehozó gázon kívül egyéb anyagot helyezünk. Mindkét jelenség mögött az rejlik, hogy a bevitt anyag a lángban, illetve a kisülésben atomjaira esik szét, és az atomok ütközések révén gerjesztett állapotba kerülnek, majd ebből az állapotból fénykibocsátás útján térnek vissza alapállapotukba. A megfigyelések szerint a kibocsátott fény vagy más elektromágneses hullám frekvenciája/hullámhossza az adott atomra jellemző. Egy adott atomhoz több ilyen jellemző frekvencia illetve hullámhossz tartozik, melyek sorozatokba rendezhetők, és együttesen alkotják az atom spektrumát (színképét). A spektrumok meghatározásával, mérésével foglalkozik a spektroszkópia tudománya. Az optikai spektroszkópiában – tehát az elektromágneses sugárzások látható és ahhoz közeli tartományában – a hullámhosszat ( ), vagy ennek reciprokát, a hullámszámot (
), vagy ennek reciprokát, a hullámszámot (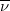 ) használják a vonalak azonosítására a frekvencia helyett. E mennyiségeket a hullámtanból jól ismert összefüggések kötik össze:
) használják a vonalak azonosítására a frekvencia helyett. E mennyiségeket a hullámtanból jól ismert összefüggések kötik össze:
![\[\nu = \frac{c}{\lambda} \qquad ; \qquad \overline\nu = \frac{1}{\lambda} = \frac{\nu}{c}\]](/images/math/8/d/0/8d06a0dc37cca7b4b07972dddb57969b.png)
ahol „c” a hullám terjedési sebessége, „ ” pedig a frekvenciája. A spektrum előállításához a fényforrás által kibocsátott fényt egy diszperzív elemre vezetik, amely a különböző hullámhosszúságú fénykomponenseket más-más irányba téríti el, így térbelileg választja szét ezeket. Az optikában leggyakrabban használt diszperzív elemek a prizma és a diffrakciós rács. Prizma esetében a diszperzió oka a törésmutató hullámhosszfüggése, melynek következtében a törési szög is függeni fog a hullámhossztól. Diffrakciós rácsoknál pedig azt használják ki, hogy az elhajlási (diffrakciós) rendek iránya erősen hullámhosszfüggő. A rácsok lehetnek reflexiósak (tükrözők) vagy transzmissziósak (fényáteresztők). Készülhetnek mechanikailag rovátkált fémből, vagy üveglapból, melyet utólag tükröző bevonattal látnak el. Gyakori emellett a holografikus rács, amit úgy állítanak elő, hogy két egymással szöget bezáró fénynyaláb interferenciaképét exponálják egy megfelelő anyagba (fotorezisztbe vagy fotopolimerbe), amely az interferenciaképet törésmutató változás formájában (azaz rácsként) rögzíti. Korszerű diszperzív eszköz továbbá az akuszto-optikai fénymodulátor, melyben egy egykristályban terjedő ultrahang hozza létre a hullámhosszának megfelelő sűrűségű rácsot. Az ultrahang hullámhossza (így a rácsperiódus) az ultrahangkeltő meghajtó jelétől függ, ezáltal akuszto-optikai modulátorból elektromosan hangolható spektrométer építhető.
” pedig a frekvenciája. A spektrum előállításához a fényforrás által kibocsátott fényt egy diszperzív elemre vezetik, amely a különböző hullámhosszúságú fénykomponenseket más-más irányba téríti el, így térbelileg választja szét ezeket. Az optikában leggyakrabban használt diszperzív elemek a prizma és a diffrakciós rács. Prizma esetében a diszperzió oka a törésmutató hullámhosszfüggése, melynek következtében a törési szög is függeni fog a hullámhossztól. Diffrakciós rácsoknál pedig azt használják ki, hogy az elhajlási (diffrakciós) rendek iránya erősen hullámhosszfüggő. A rácsok lehetnek reflexiósak (tükrözők) vagy transzmissziósak (fényáteresztők). Készülhetnek mechanikailag rovátkált fémből, vagy üveglapból, melyet utólag tükröző bevonattal látnak el. Gyakori emellett a holografikus rács, amit úgy állítanak elő, hogy két egymással szöget bezáró fénynyaláb interferenciaképét exponálják egy megfelelő anyagba (fotorezisztbe vagy fotopolimerbe), amely az interferenciaképet törésmutató változás formájában (azaz rácsként) rögzíti. Korszerű diszperzív eszköz továbbá az akuszto-optikai fénymodulátor, melyben egy egykristályban terjedő ultrahang hozza létre a hullámhosszának megfelelő sűrűségű rácsot. Az ultrahang hullámhossza (így a rácsperiódus) az ultrahangkeltő meghajtó jelétől függ, ezáltal akuszto-optikai modulátorból elektromosan hangolható spektrométer építhető.
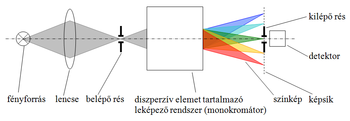
A spektrométerek működési elvét az 1. ábra mutatja: a vizsgálandó fényforrás fényét (pl. egy lencsével) összegyűjtjük a spektrométer belépő résén, ami egy 0-tól néhány tized mm-ig állítható szélességű keskeny téglalap. Ezt a rést egy erősen diszperzív elemet tartalmazó leképező rendszerrel (ún. monokromátorral, amely a jelen mérés során egy reflexiós elven működő diffrakciós rácsot tartalmaz) leképezik. A belépő rés képe megsokszorozva, minden egyes hullámhosszra más pozícióban jelenik meg a spektrométer képsíkjában, ld. 2. b. ábra és 2. c. ábra. Az így nyert spektrumot egészében rögzíthetik fotólemezen, vagy pixelezett fénydetektorral (CCD). Nagy érzékenységű műszerekben (miként a jelen mérésben is) detektorként fotoelektron sokszorozót használnak, amely nem pixelezett, így önmagában nem képes spektrális információt szolgáltatni. Ebben az esetben adott hullámhossz komponens a spektrométer képsíkjába helyezett másik (ún. kilépő) réssel választható ki. A teljes színkép felvételekor vagy a kilépő rés-detektor együttest mozgatják végig a spektrumon, vagy a hullámhossz szerint szétválasztott nyalábot pozícionálják úgy, hogy a színképnek mindig más és más része essen a kilépő résre. A mérés során alkalmazott spektrométerben ez utóbbi megoldást használjuk a hidrogén atom és más fényforrások színképének meghatározására.
A hidrogén atom
Az atomok eletronhéja fénykibocsájtás során egy nagyobb energiájú gerjesztett állapotból pillanatszerűen átalakul egy kisebb energiájú alapállapotba, miközben egy – a két állapot ΔE energiakülönbségével egyenlő energiájú – fotont sugároz ki. A foton energiája és frekvenciája ( ) közötti kapcsolatot a jól ismert képlet írja le:
) közötti kapcsolatot a jól ismert képlet írja le:
![\[\Delta E = h\cdot\nu\]](/images/math/a/f/3/af3c598512162a612f6189608a93b29f.png)
ahol „h” a Planck-állandó. Előzetes tanulmányainkban (a Bohr-féle atommodell alapján, vagy a hidrogén atom Schrödinger-egyenletének megoldásával) meghatároztuk a hidrogén atom elektronburkának lehetséges En energiáját:
![\[E_n = -\frac{m\cdot e^4}{8\cdot\epsilon_0^2\cdot h^2}\cdot\frac{1}{n^2}\]](/images/math/4/a/d/4ad22e20dfb51aab4057e6833413cb37.png)
ahol n = 1, 2, 3, ... az elekronhéjak energiaszintjeit leíró ún. főkvantumszám, „m” és „e” az elektron tömege ill. töltése, 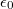 pedig a vákuum dielektromos permittivitása. Mivel elektronátmenet csak egyik héjról a másikra lehetséges, ezért a kisugárzott fotonenergia értéke egyenlő a gerjesztett (n1) és az alapállapot (n0) energiáinak különbségével:
pedig a vákuum dielektromos permittivitása. Mivel elektronátmenet csak egyik héjról a másikra lehetséges, ezért a kisugárzott fotonenergia értéke egyenlő a gerjesztett (n1) és az alapállapot (n0) energiáinak különbségével:
![\[\Delta E = E_{n_1} - E_{n_0} = \frac{m\cdot e^4}{8\cdot\epsilon_0^2 \cdot h^2} \cdot \left( \frac{1}{n_0^2} - \frac{1}{n_1^2}\right) = h\cdot\nu\]](/images/math/4/3/1/431cc5780b5a82d81c8cfe93c297886c.png)
Ebből (1) alapján kifejezhető a kisugárzott foton hullámszáma:
![\[\overline\nu = \frac{\Delta E}{c\cdot h} = \frac{m\cdot e^4}{8\cdot c\cdot\epsilon_0^2 \cdot h^3} \cdot \left( \frac{1}{n_0^2} - \frac{1}{n_1^2}\right) = R_{\infty} \cdot \left(\frac{1}{n_0^2} - \frac{1}{n_1^2}\right) \Rightarrow \frac{1}{\lambda} = R_{\infty} \cdot \left(\frac{1}{n_0^2} - \frac{1}{n_1^2}\right)\]](/images/math/0/7/e/07eda7a11e332112021268a83e1e3b24.png)
ahol 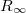 a Rydberg-állandó. A jelölésben alkalmazott „∞” szimbólum azt jelenti, hogy az energia (3) képletének levezetésénél az atommag tömegét végtelen nagynak tekintettük az elektronéhoz képest. Az elhanyagolás miatt hidrogén esetében
a Rydberg-állandó. A jelölésben alkalmazott „∞” szimbólum azt jelenti, hogy az energia (3) képletének levezetésénél az atommag tömegét végtelen nagynak tekintettük az elektronéhoz képest. Az elhanyagolás miatt hidrogén esetében 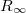 -től csekély eltérést tapasztalunk. A kis korrekció miatt a hidrogén atom Rydberg-állandója:
-től csekély eltérést tapasztalunk. A kis korrekció miatt a hidrogén atom Rydberg-állandója: 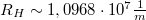 . Az alapállapot főkvantum-számának (n0) rögzítésével emissziós sorozatokat kapunk, melyek közül az n0 = 2 (az ún. Balmer-sorozat) adja a hidrogén látható színképét. A Balmer-sorozat első négy tagja (n1 = 3, 4, 5, 6) esik az emberi szemmel látható fény tartományába (ezeket Hα, Hβ, Hγ, Hδ-val jelölik). Ez a spektrum, valamint egy hidrogén lámpa képe látható a 2. ábrán.
. Az alapállapot főkvantum-számának (n0) rögzítésével emissziós sorozatokat kapunk, melyek közül az n0 = 2 (az ún. Balmer-sorozat) adja a hidrogén látható színképét. A Balmer-sorozat első négy tagja (n1 = 3, 4, 5, 6) esik az emberi szemmel látható fény tartományába (ezeket Hα, Hβ, Hγ, Hδ-val jelölik). Ez a spektrum, valamint egy hidrogén lámpa képe látható a 2. ábrán.
A mérési elrendezés
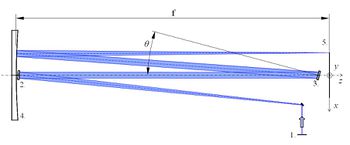
Az elrendezés az 1. ábrán látható vázlatnak megfelelően van kialakítva. A mérésben alkalmazott PGS-2 típusú német gyártmányú spektrométer monokromátorának működését a 3. ábra szemlélteti. A fényforrást egy lencse segítségével a spektrométer 0-0,3 mm között állítható szélességű belépő résére képezzük közel egy az egyes nagyítással. A résből kiinduló fénysugarakat az „f” fókusztávolságú homorú segédtükör párhuzamosítja, így jutnak a forgatható optikai rácsra, majd onnan visszatükröződve a szintén „f” fókusztávolságú homorú főtükörre. A tükör a sugarakat a kilépő résre fókuszálja, így végül a kilépő rés síkjában a belépő rés 1:1-arányú képe jelenik meg x-irányban hullámhosszakra bontva. A homorú tükör alkalmazásának egyik előnye, hogy ellentétben a lencsékkel nincs színi hibája, azaz fókusztávolsága minden hullámhosszon azonos, és színtorzítása (transzverzális kromatikus aberrációja) nulla. A kilépő rés az x ≈ 0 pozícióban van elhelyezve, ehhez szorosan, fényzáró módon illeszkedik a photomultiplier (fotoelektron sokszorozó) detektor, melynek erősített jelét egy voltmérővel mérjük. Tekintsük át az elrendezés elemeit!
A fényforrás egy függőlegesen elhelyezett kisülési cső, melyben hidrogén gáz található (ld. 2.a. ábra ). Ezt 3,4 kV-os és 3,5 mA-es egyenárammal gerjesztjük (vigyázat, nagyfeszültség!). A kisülésben az eredetileg molekuláris állapotú hidrogén egy része atomjaira esik, majd ezek az elektronokkal ütközve gerjesztődnek, ionizálódnak. Az így létrejövő keverék spektrumában az atomi színképvonalak is karakteresen megjelennek, de mellette a 2.c. ábrán látható háttérspektrum is létrejön. A 2.a. ábrán is látható módon a kisülés nem egyszínű. A mérés során igyekezzünk a ciklámen színű (rózsaszín) kisülésdarabot a belépő résre képezni, mert ez jellemző az atomi hidrogén kisugárzására.
A spektrométer egy hálózati főkapcsolóval (Netz) valamint egy fényzárral (Verschluss) is rendelkezik. A rácsot egy 100-as beosztású forgatógombbal lehet elfordítani. Egy teljes fordulat egy fokot fordít, a θ szöghelyzetet (ld. 3. ábra) pedig egy egyfokos beosztású skálán lehet leolvasni. A skála és a forgatógomb együttes állása mutatja a századfok pontos szöget (lásd 4. ábra). A szöghelyzethez tartozó, a kilépő résre eső hullámhosszt a monokromátor alábbi egyenlete adja meg (levezetést ld. a mellékletben):
![\[k\cdot\lambda = \frac{2}{G}\cdot\sin(\theta)+x\cdot\frac{\cos(\theta)}{f\cdot G} \left[mm\right]\]](/images/math/7/0/7/707bd60df6fb533c3c25234e08c3efe5.png)
ahol  a kijelzett szögállás, „k” a diffrakció rendje (mérésünkben k = 1), f = 2075 mm (a PGS-2 homorútükrének fókusztávolsága), és G = 651,5 mm−1 (a PGS-2 diffrakciós rácsának térfkervenciája, azaz a milliméteren-kénti osztásszám.) Az „x” a spektrométer kilépő résének pozíciója [mm]-ben. Jelen esetben értéke bizonytalan: x = −2..+2 mm, ami a mérést hibával terheli.
a kijelzett szögállás, „k” a diffrakció rendje (mérésünkben k = 1), f = 2075 mm (a PGS-2 homorútükrének fókusztávolsága), és G = 651,5 mm−1 (a PGS-2 diffrakciós rácsának térfkervenciája, azaz a milliméteren-kénti osztásszám.) Az „x” a spektrométer kilépő résének pozíciója [mm]-ben. Jelen esetben értéke bizonytalan: x = −2..+2 mm, ami a mérést hibával terheli.
A photomultipliert egy nagyfeszültségű (kb. 600 V-os) tápegység működteti, voltmérésre pedig egy asztali multimétert használunk (célszerűen 20 V-os méréshatárban). Működéséből eredően a detektor jele nulla megvilágítás esetén sem zérus, ezt hívják sötétzajnak (értéke kb. 0,08 V). A spektrométer fényzárjának bezárásakor megállapítható az átlagos értéke, melyet a továbbiakban ki kell vonni a mért feszültségekből.
Mérési feladatok
1. feladat: A spektrométer kalibrálása
A mérés célja a PGS-2 spektrométer kalibrálása a Balmer-formula segítségével, ugyanis a Rydberg-állandóban csak univerzális állandók szerepelnek mint tényezők, ezért független a környezeti paraméterektől (pl: nyomás, hőmérséklet…). A hidrogén kisülési lámpa fényében több emissziós sorozat megjelenik, azért a Balmer sorozatot használjuk, mert ez esik a látható tartományba, és itt érzékeny a fény detektálására használt fotoelektron sokszorozó. Kapcsolja be a kisülési csövet, a detektort ellátó tápegységet valamint a spektrométert és a feszültségmérőt. A fotoelektron sokszorozó feszültségét állítsa 600 V-ra. A Hidrogén lámpa bemelegedési ideje kb. 15 perc. Ellenőrizze a kisülési cső leképezését a belépő résre, ha szükséges, állítsa be megfelelően. A beállítást segíti, ha a rés mérete nem túl kicsi, mert nagyobb résméretnél nagyobb jeleket lehet mérni, de a külső háttérfény is jobban beszűrődik. Az „éles” mérések előtt állítsa be- illetve kilépő réseket 0,1 mm szélesre.
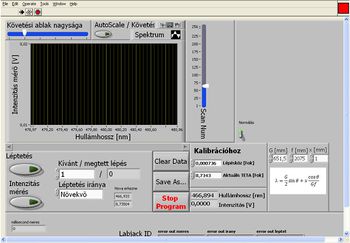
Kapcsolja be a számítógépen a spektrométer adatgyűjtő programját (kezelőfelületet ld. 5. ábrán) és ellenőrizze, hogy a program által kijelzett szögérték („Aktuális TETA”) megegyezik-e a spektrométeren kijelzettel. Amennyiben szükséges, adja meg a programnak a helyes szögértéket. A hullámhossz kalibráláshoz kapcsolja ki a normálást (ez a tényező a detektor hullámhosszfüggését küszöböli ki). Az (5) összefüggés alapján számítsa ki a Balmer-sorozat első négy elemének (Hα, Hβ, Hγ, Hδ) hullámhosszát. Állítsa be a lépésszámot és az irányt úgy, hogy ez a négy elem beleessen a mérés hullámhossz tartományába, törölje a korábban mért adatokat („Clear Data”), majd indítsa el a léptetést.
A léptetés végén mentse el az adatokat („Save As...”), és ellenőrizze, hogy a számítógép által lejegyzett szögérték megegyezik-e a valóságossal! Mekkora eltérést tapasztal? Becsülje meg ez mekkora eltérést eredményezhet hullámhosszban! A rések 0,1 mm-es szélessége hány nm-nek felel meg ebben a spektrométerben? A mért Hα, Hβ, Hγ, Hδ hullámhossz-szögérték adatok alapján (6) segítségével határozza meg az „x” paramétert! (Pl. mind a négy hullámhosszra kiszámítani x-et, majd átlagolni.)
2. feladat: LED spektrumának meghatározása
Tegye a fény emittáló diódát (LED) egész közel a belépő réshez. FIGYELEM: a mérésvezérlő szoftver 0-10 V méréstartományban működik, ennek megfelelően kell a fényforrást elhelyezni a rés előtt (túl sok fény esetén távolítani, kevés esetén közelíteni kell a LED-et). A tápegységen állítson be áramkorlátnak 20 mA-t, feszültségkorlátnak 3,5 V-ot. Csatlakoztassa a diódát a tápegységhez (a hosszabb lábat a pozitív pólushoz). Milyen színű fényt bocsát ki a dióda? Ennek megfelelő hullámhossztartományt rögzítsen a számítógép segítségével, ehhez használja a normálás funkciót! FIGYELEM: technikai okokból a detektor érzékenységét 370-840 nm hullámhossz tartományban kalibráltuk, a kalibráció hibája kb. ±3%. Vizsgálja meg hogyan változik a spektrum, ha 10 mA-re lecsökkenti a diódaáramot! Az átállításhoz az on/off gombbal vegye le a feszültséget! Mindkét spektrumot mentse el, és az előző pontban kiszámított x-et behelyettesítve ábrázolja azokat!
Melléklet: a monokromátor egyenletének levezetése
A fizikából tanultak alapján diffrakciós rácsok esetében a beeső fénysugár felületnormálissal bezárt szöge (α−θ), és a „k”-ik rendbe diffraktált fénysugár felületnormálissal bezárt szöge (β+θ) között az álábbi összefüggés áll fönn (magyarázat ld. a 6.a. ábrán):
![\[\sin(\beta+\theta) - \sin(\alpha-\theta)= k\cdot G \cdot \lambda \qquad (G = \frac{1}{d},\ d\ a\ r\acute{a}cs\acute{a}lland\acute{o})\]](/images/math/f/6/6/f661b707a521fdfea84cd9bd0ad8aa6d.png)
ahol „G” a rács rovátkáinak térfrekvenciája, α a beeső fénysugár és β a diffraktált fénysugár z-tengellyel (azaz a homorú főtökör forgástengelyével) bezárt szög (figyelem: β és θ előjeles szögek!). A fenti egyenlet trigonometrikus azonosságok alapján így írható át:
![\[\sin(\beta) \cdot \cos(\theta) + \cos(\beta) \cdot \sin(\theta) - \sin(\alpha) \cdot \cos(\theta) + \cos(\alpha) \cdot \sin(\theta)= k\cdot G \cdot \lambda\]](/images/math/3/9/d/39ddad522053b4d452257d179f3e2521.png)
Szintén korábbi ismereteink alapján tudjuk, hogy „f” fókusztávolságú leképezőrendszer esetében a β tárgyszög és a hozzá tartozó fókuszpont x-koordinátája közötti kapcsolat a következő alakú:
![\[x = f \cdot tg(\beta)\]](/images/math/8/4/3/84365ac57b5340b6cb566d978a739f37.png)
(9)-ből kifejezhető sin(β) és cos(β):
![\[sin(\beta) = \frac{x}{ \sqrt{f^2+x^2} } \qquad cos( \beta) = \frac{f}{ \sqrt{f^2+x^2} }\]](/images/math/5/a/2/5a22d3191d543b73bee3db3888109769.png)
Ezt visszahelyettesítve (8)-ba, és átrendezve a kapott egyenletet:
![\[k \cdot G \cdot \lambda = \sin(\theta) \cdot \left[ \frac{f}{ \sqrt{f^2+x^2} } + \cos(\alpha)\right] + \cos(\theta) \cdot \left[ \frac{x}{ \sqrt{f^2+x^2} } - \sin(\alpha)\right]\]](/images/math/2/0/2/2021b5933194a2c31bd0c2a0188e1717.png)
A PGS-2 spektrométer monokromátorának esetében α ≈ 0 és x << f. Ezekkel a közelítésekkel (11) jelentősen leegyszerűsödik:
![\[k \cdot G \cdot \lambda = \sin(\theta) \cdot 2 + x \cdot \frac{\cos(\theta)}{f} \Rightarrow k\cdot \lambda = \frac{2}{G}\cdot\sin(\theta) + x\cdot \frac{\cos(\theta)}{f \cdot G}\]](/images/math/e/7/b/e7b72b8da1e529b9e5d35106f88c764a.png)
amivel megkaptuk a keresett (6) egyenletet, amely előjelhelyesen írja le x és θ kapcsolatát.
PDF formátum