„Kvantumpöttyök” változatai közötti eltérés
(→Kvantum pöttyök, energia skálák) |
(→Kvantum pöttyök, energia skálák) |
||
| 90. sor: | 90. sor: | ||
ahol $\alpha$ egy $N$ független szám. A fentiek alapján a kapufeszültség hatása egy $Q_0=V_G C_G$ un. offset töltéssel azonos. | ahol $\alpha$ egy $N$ független szám. A fentiek alapján a kapufeszültség hatása egy $Q_0=V_G C_G$ un. offset töltéssel azonos. | ||
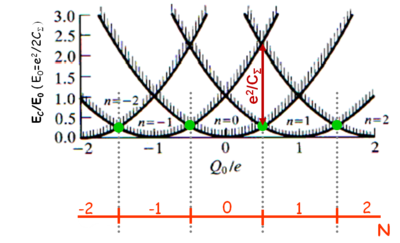
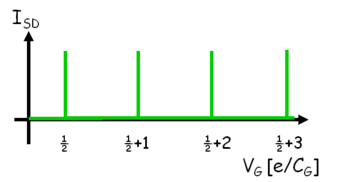
| − | Az elektrosztatikus energiára kapott $E_C$ kifejezés az 5.a ábrán látható az offset töltés függvényében különböző $N$ elektron számok mellett. Az ábra alapján minden egyes $Q_0$ értékre könnyen meghatározható, hogy milyen elektron szám fogja minimalizálnia a kvantum pötty energiáját. A piros tengelyen a pötty alapállapotához tartozó elektron szám van feltüntetve. Az ábrán jelölt zöld pontokban a kvantum pötty alapállapota degenerált. Például a $Q_0/e=1/2$ helyen az $N=0$ és $N=1$ állapotok energiája azonos. Ezekben a speciális pontokban az egyik elektródáról egy elektron be tud ugrani a kvantum pöttyre energia költség nélkül és az elektron ki tud ugrani a másik elektródára. Ezen szekvenciális elektron alagutazási folyamaton keresztül áram tud folyni a kvantum pöttyön keresztül ha kis $V_{SD}$ feszültséget kapcsolunk a két elektróda közé. 5.b ábra mutatja a kvantum pöttyön átfolyó áramot az offset töltéssel arányos kapufeszültség függvényében (kis $V_{SD}$ mellett). Az áram a $V_G$ paramétertér nagyrészében nulla leszámítva egymástól egyenlő távolságban található pontokat, ahol az áram csúcsszerűen megnő. Ezeket hívjuk ún. Coulomb-csúcsoknak. Véges áramot csak ezen degenerációs pontokban kapunk | + | Az elektrosztatikus energiára kapott $E_C$ kifejezés az 5.a ábrán látható az offset töltés függvényében különböző $N$ elektron számok mellett. Az ábra alapján minden egyes $Q_0$ értékre könnyen meghatározható, hogy milyen elektron szám fogja minimalizálnia a kvantum pötty energiáját. A piros tengelyen a pötty alapállapotához tartozó elektron szám van feltüntetve. Az ábrán jelölt zöld pontokban a kvantum pötty alapállapota degenerált. Például a $Q_0/e=1/2$ helyen az $N=0$ és $N=1$ állapotok energiája azonos. Ezekben a speciális pontokban az egyik elektródáról egy elektron be tud ugrani a kvantum pöttyre energia költség nélkül és az elektron ki tud ugrani a másik elektródára. Ezen szekvenciális elektron alagutazási folyamaton keresztül áram tud folyni a kvantum pöttyön keresztül ha kis $V_{SD}$ feszültséget kapcsolunk a két elektróda közé. 5.b ábra mutatja a kvantum pöttyön átfolyó áramot az offset töltéssel arányos kapufeszültség függvényében (kis $V_{SD}$ mellett). Az áram a $V_G$ paramétertér nagyrészében nulla leszámítva egymástól egyenlő távolságban található pontokat, ahol az áram csúcsszerűen megnő. Ezeket hívjuk ún. Coulomb-csúcsoknak. Véges áramot csak ezen degenerációs pontokban kapunk közöttük az elektronok átjutás a pöttyön blokkolva van. Ezt a jelenséget hívják ún. Coulomb-blokádnak, ami a kvantum pöttyök egyik fontos tulajdonsága. A Coulomb-blokád az elektronok közötti taszító Coulomb-kölcsönhatás és az elektromos töltés kvantáltságának a következménye. A kvantum pöttyön az elektron szám jól meghatározott és ennek következtében áram nem tud a pöttyön keresztül folyni egészen addig, amíg az offset töltés változtatásával degenerációs pontba nem hangoljuk az elektron szigetet. (A degenerációs pontok távolsága $\Delta Q_0=1$). |
| 102. sor: | 102. sor: | ||
|} | |} | ||
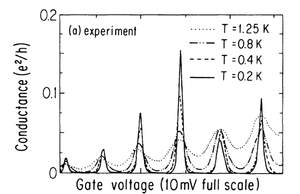
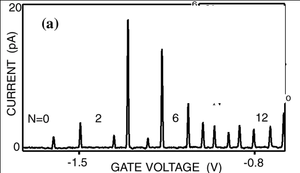
| − | A kapott elméleti várakozásokat vessük össze kvantum pöttyökön mért tipikus kísérleti eredményekkel. A 6. ábrán láthatóak vezetőképesség ($G=I/V_{SD}$) mérések a kapufeszültség függvényében (kis $V_{SD}$ mellett). Alacsony hőmérsékleten éles csúcsok jelentkeznek, amiket nulla vezetőképességű tartományok határolnak el a Coulomb-blokádnak megfelelően. A 6.a ábrán a csúcsok egyenletesen helyezkednek el $V_G$ tengely mentén az elektrosztatikus képben kapott eredményekkel összhangban. A hőmérséklet növelésével a csúcsok elmosódnak és a köztes völgyekben az áram egyre nagyobbra nő. Ez a termikus elmosódás akkor válik jelentőssé, ha a pötty hőmérséklete összemérhetővé válik | + | A kapott elméleti várakozásokat vessük össze kvantum pöttyökön mért tipikus kísérleti eredményekkel. A 6. ábrán láthatóak vezetőképesség ($G=I/V_{SD}$) mérések a kapufeszültség függvényében (kis $V_{SD}$ mellett). Alacsony hőmérsékleten éles csúcsok jelentkeznek, amiket nulla vezetőképességű tartományok határolnak el a Coulomb-blokádnak megfelelően. A 6.a ábrán a csúcsok egyenletesen helyezkednek el $V_G$ tengely mentén az elektrosztatikus képben kapott eredményekkel összhangban. A hőmérséklet növelésével a csúcsok elmosódnak és a köztes völgyekben az áram egyre nagyobbra nő. Ez a termikus elmosódás akkor válik jelentőssé, ha a pötty hőmérséklete összemérhetővé válik az elektrosztatikus energiaskálával: $k_B T \approx E_C$. A 6.b ábrán is egy hasonló mérés látható, a Coulomb-csúcsok itt is megjelennek, ugyanakkor a csúcsok távolsága nem egyenletes, ahogyan az egyszerű modellünkből várnánk. Ennek megértéséhez már az elektrosztatikus képen túl kell lépni és a pötty bezáró potenciáljában kialakuló diszkrét elektron állapotokat figyelembe kell vennünk. Ilyen viselkedést a kisebb méretű kvantum pöttyökben tapasztalhatunk. |
| + | |||
| + | |||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
A lap 2013. június 30., 21:24-kori változata
Szerkesztés alatt!
Q.
Hát erről lesz szó, csak kicsit bővebben.
Tartalomjegyzék |
Kvantum pöttyök, energia skálák
Korábban láttunk páldákat olyan nanoszerkezetekre, ahol az elektronok mozgása csak két illetve egy dimenzióban megengedett (GaAs/AlGaAs határfelületen létrejövő 2 dimenziós elektrongázok ill. pontkontaktusok). Ezen alacsony dimenziós szerkezetek olyan érdekes jelenségek megfigyelését teszik lehetővé, mint a kvantált Hall-effektus vagy a vezetőképesség kvantálás (linkek). Ebben a fejezetben egy további alacsony dimenziós nanoszerkezet családdal fogunk foglalkozni, az un. kvantum pöttyökkel (kvantum dotokkal), ahol az elektronok mozgását mind a három dimenzió mentén megszorítjuk. Ezen nulla dimenziós szerkezetek egy mesterséges szigetet jelentenek az elektronok számára, amik tipikus sugara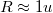 
m
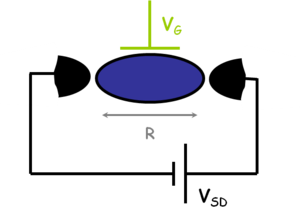
m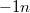 (lásd 1. ábra). Kvantum pöttyöket gyakran a térvezérelt tranzisztorokhoz hasonló áramkörökbe építik (link): két elektródát kapcsolnak a szigethez (forrás/source és nyelő/drain), amikből elektronok juthatnak a szigetre és távozhatnak onnet. Ezt egy harmadik, un. kapu/gate elektróda egészíti ki, ami a sziget elektromos potenciájának változtatását teszi lehetővé. A továbbiakban ilyen térvezérelt geometriájú kvantum pöttyöket fogunk tárgyalni.
 |
1. ábra Kvantum pötty/dot áramkörbe építve. Egy  sugarú sziget, forrás/source és nyelő/drain elektródág között (fekete) illetve egy kapu/gate elektródához csatolva (zöld).
|
Megvalósítás
Kvantum pöttyöket különböző módszerekkel lehet létrehozni. Ezekre lássunk néhány példát:
- Egy kétdimenziós elektron gázra kapuelektródákat téve, az elektródákra adott negatív feszültséggel a kapu elektródák alól az elektronok kiszorulnak. A kapukat megfelelően elrendezve létre lehet hozni szigeteket az elektron gázból, amik kvantum pöttyként viselkednek (lásd. 3a ábra). A kapukra adott feszültség változtatásával
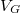a pötty potenciálja hangolható.
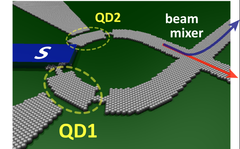
- Kvantum pöttyök készíthetőek változatos nanoszerkezetekből: szén nanocsövekből, félvezető nanopálcákból, grafénból. 3b. ábra mutat egy példát grafén kvantum pöttyre. Plazma marással egy szigetet vágunk ki a szén síkból, ami elvékonyított részekkel kapcsolódhat az elektródákhoz.
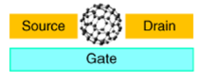
- Elektródák közé juttatott nagyobb molekula (pl. fullerén) is mutathat kvantum pötty viselkedést (lásd. 3.c ábra). A molekulák kis méretéből adódóan (
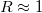nm)a három elektróda elhelyezése problémás.
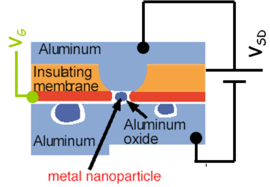
- Kvantum pöttyként működnek kis fémes szemcsék is. Ha ezeket szigetelő rétegbe ágyazzuk és fém elekródákat hozunk létre mellettük, a szokásos forrást, nyelőt és kapu elektródát tartalmazó geometria létrehozható (lásd. 3.d ábra).
 |
 |
 |
 |
| 3a. ábra 2DEG-ban kapuelektródákkal létrehozott kvantum pötty. A fekete körvonalú szürke területek a kapu elektródák, a rájuk kapcsolt negatív feszültség hozza létre az elektronok csapdázó potenciálját. A zölddel jelölt elektródára adott feszültség szolgál a potenciálgödör hangolására. Elektronok a sárga tartományban vannak. [1] | 3b. ábra Grafénből kimart szerkezet két kvantum pöttyel (QD1 és QD2) | 3c. ábra Molekulán alapuló kvantum pötty [2] | 3d. ábra Oxidba ágyazott fém nanoszemcsén alapuló kvantum pötty [2] |
Energia skálák
Kvantum pöttyre helyezett elektronok viselkedését a sziget bezáró potenciája, az elektronok közötti taszitó kölcsönhatás illetve a szigeten töltött átlagos idejük jelentősen befolyásolja. Tekintsük át az ezekhez kapcsolódó energiaskálákat:
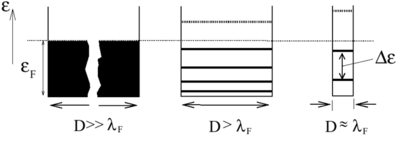
- Szint távolság (Level spacing,
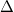): Ha a kvantum pötty mérete nem sokkal nagyobb, mint a Fermi-hullámhossz, azaz 
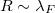, az elektronok hullám természetét figyelembe kell venni. Az elektronok a sziget bezáró potenciája által meghatározott hullámfüggvényeket tölthetik be, melyekhez a folytonos energia spektrum helyett diszkrét energiaszintek tartoznak, ha a pötty mérete elegendően kicsi (lásd 2a ábra). A diszkrét energiaszintek átlagos távolságát hívjuk szinttávolságanak, 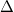. A szint távolság például két dimenziós kvantum pötty esetén 
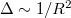. Tipikus értéke 
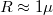m esetén 
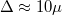eV.
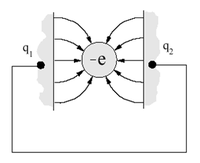
- Elektrosztatikus energia (Charging energy,
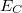): Az elektronok között fellépő Coulomb-taszítás miatt energia költséggel jár ha újabb és újabb elektronokat akarunk helyezni a kvantum pöttyre. Egyszerű elektrosztatikus képben (lásd. 2b. ábra) ezt a többlet energiát, a pötty és a környezete közötti kapacitás 
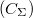határozza meg, 
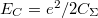. A szigetet sugarú gömbbel közelítve,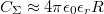 
alapján, 
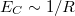függést kapunk. Maradva a két dimenziós elektron gázból kialakított pötty példájánál, egy 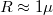m pötty esetében: 
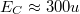eV.
- Kvantum fluktuációk energia bizonytalansága: Mivel a kvantum pötty alagút átmeneteken keresztül csatolva van az elektródákhoz, a pöttyre helyezett elektronok véges valószínűséggel távozhatnak a pöttyről, ami a sziget eneriaszintjeinek a kiszélesedéséhez vezet. A Heisenberg-féle határozatlansági reláció alapján a kiszélesedés mértéke:
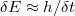, ahol h a Plank-állandó 
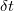pedig az átlagos idő, amit az elektron a pöttyön tartózkodik. Az utóbbit megbecsülhetjük az alagútátmenet ellenállása (
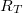) és kapacitása (
) alapján: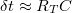 
. Ahhoz hogy a kvantum pötty viselkedést a fluktuációk ne mossák el, megköveteljük, hogy 
. 
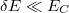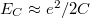-t kihasználva az alagútátmenet ellenállására a következő megszorítást kapjuk: 
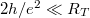. Az ellenállás kvatumot bevezetve 
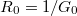, ahol 
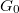a korábban definiált vezetőképesség kvantum (link) 
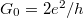, a feltételt átírhatjuk: 
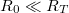. Azaz az alagútátmenet ellenállását nagyobbra kell választani az ellenállás kvantumnál, hogy a kvantum pötty viselkedés megfigyelhető legyen.
A kapott számok alapján látható, hogy egy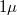 
m körüli kvantum pöttynél az elektrosztatikus energia lényegesen nagyobb, mint a szint távolság. Ugyanakkor ha a kvantum pötty méretét csökkentjük, a szinttávolság erősebb méretfüggéséből adódóan, a két skála azonos nagyságúvá válhat. Ha tekintjük a legkisebb kvantum pöttyöket, egyetlen atomot vagy molekulát, ott már a szinttávolság a domináns energia skála. Az atomok elektronszerkezetét (azaz a periódusos rendszert) elsődlegesen a mag vonzó potenciáljában kialakuló hullámfüggvényekhez tartozó diszkrét energiaszintek határozzák meg és az elektronok közötti Coulomb-kölcsönhatás csak korrekciót ad ehhez.
 |
 |
| 2a. ábra Kvantum bezártságból adódó energia szintek [1] | 2b. ábra Kvatum pöttyre helyezett elektron elektrosztatikus energiája [1] |
Kvantum pöttyök leírása elektrosztatikus képben
Kvantum pöttybe zárt elektronok eneregiája az elektronok kinetikus energiájából, a bezáró potenciál és az elektronok között fellépő elektron-elektron kölcsönhatásból adódik össze. Az elektronok közötti taszításból származó többlet energiát egyszerűen közelíhetjük elektrosztatikus képben a kvantum pötty és a környezete közötti kapacitások figyelembe vételével. Az előző részben kapott becslések alapján láttuk, hogy egy átlagos méretű kvantum pötty esetén a kinetikus energiát és a bezáró potenciált együttesen jellemző szinttávolság lényegesen kisebb, mint a kapacitások alapján becsült elektrosztatikus energia; így a következőkben kizárólag az elektrosztatikus energia tagot megtartva adunk leírást a kvantum pöttyök viselékedésére. Látni fogjuk, hogy a kvantum pöttyök alapvető jelenségei (mint például a Coulomb-blokád, Coulomb-gyémánt szerkezet, egy elektron tranzisztor viselkedés ...) már ebben az egyszerű képben is megérthetőek.
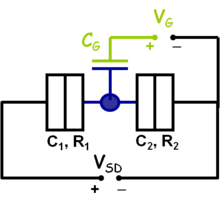
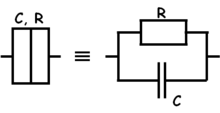
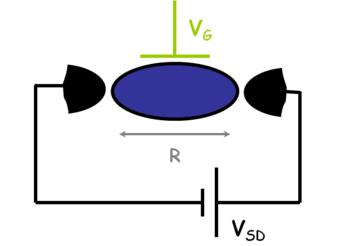
Az 1. ábrán látható áramkörbe épített kvantum pöttyöt elektrosztatikus képben a 4. ábrán látható módon helyettesíthetjük. A pötty területe (kék) két alagútátmeneten keresztül kapcsolődik a forrás és a nyelő oldal közé kapcsolt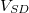 
feszültség forráshoz. Az alagútátmeneteket párhuzamosan kapcsolt kapacitással () és ellenállással modellezhetjük (). A kapacitás fegyverzeteit az alagútátmenet által elválasztott két közeli felület adja, a tipikusan nagy ellennállás érték pedig az alagútátmeneten történő átjutást jellemzi. A kvantum pötty közelében található kapuelektródát (zöld) a sziget és az elektróda közötti kapacitással irhatjuk le (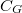
). A kapu elektródára kapcsolt 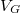feszültség segítségével lehet majd a pötty betöltöttségét hangolni.
 |
 |
| 4a. ábra Kvantum pötty elektrosztatikus helyettestő képe | 4b. ábra Az elektródákat elválasztó alagútátmenetek helyettesítő képe |
Elektrosztatikus közelítésben a kvantum pötty energiája a pöttyöt körbehatároló kapacitások segítségével a következőkéépen irhatjuk fel:
![\[E_C (N, V_{SD}=0, V_G = 0) = (Ne)^2/2C_{\Sigma}\]](/images/math/6/2/1/621721a5f701d76365a6bd2da5fcf35d.png)
ahol 
a kvantum pöttyön lévő elektronok száma,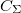 
pedig a pötty és a környezete közötti összkapacitás: 
.
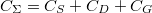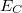kifejezése alapján, ha az elektronok számát növelni akarjuk eggyel, az a következő többlet energiába kerül: 
.
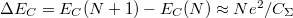Véges kapufeszültség esetén vigyázni kell az energia felírásakor, hiszen az elektronok pöttyre helyezése során a kapu telepe is munkát végez, ami csökkenti a feltöltéshez szükséges energiát. Ha a pöttyre helyezett töltés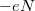 
, akkor a párhuzamosan kapcsolt kapacitások miatt a kapu elektróda fegyverzetén 
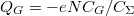töltés lesz. A pötty energiáját a telep
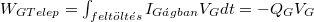munkavégzésével korrigálva kapjuk: 
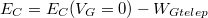. Mindezek alapján:
![\[E_C (N, V_{SD}=0, V_G) = 1/2C_{\Sigma}(Ne-V_G C_G)^2 + \alpha\]](/images/math/d/a/b/dab58959ce356b9dd6071a745607c6f2.png)
ahol 
egy független szám. A fentiek alapján a kapufeszültség hatása egy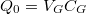 
un. offset töltéssel azonos.
Az elektrosztatikus energiára kapott 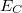kifejezés az 5.a ábrán látható az offset töltés függvényében különböző elektron számok mellett. Az ábra alapján minden egyes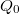 
értékre könnyen meghatározható, hogy milyen elektron szám fogja minimalizálnia a kvantum pötty energiáját. A piros tengelyen a pötty alapállapotához tartozó elektron szám van feltüntetve. Az ábrán jelölt zöld pontokban a kvantum pötty alapállapota degenerált. Például a 
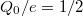helyen az 
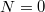és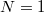 
állapotok energiája azonos. Ezekben a speciális pontokban az egyik elektródáról egy elektron be tud ugrani a kvantum pöttyre energia költség nélkül és az elektron ki tud ugrani a másik elektródára. Ezen szekvenciális elektron alagutazási folyamaton keresztül áram tud folyni a kvantum pöttyön keresztül ha kis 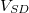feszültséget kapcsolunk a két elektróda közé. 5.b ábra mutatja a kvantum pöttyön átfolyó áramot az offset töltéssel arányos kapufeszültség függvényében (kis 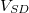mellett). Az áram a 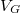paramétertér nagyrészében nulla leszámítva egymástól egyenlő távolságban található pontokat, ahol az áram csúcsszerűen megnő. Ezeket hívjuk ún. Coulomb-csúcsoknak. Véges áramot csak ezen degenerációs pontokban kapunk közöttük az elektronok átjutás a pöttyön blokkolva van. Ezt a jelenséget hívják ún. Coulomb-blokádnak, ami a kvantum pöttyök egyik fontos tulajdonsága. A Coulomb-blokád az elektronok közötti taszító Coulomb-kölcsönhatás és az elektromos töltés kvantáltságának a következménye. A kvantum pöttyön az elektron szám jól meghatározott és ennek következtében áram nem tud a pöttyön keresztül folyni egészen addig, amíg az offset töltés változtatásával degenerációs pontba nem hangoljuk az elektron szigetet. (A degenerációs pontok távolsága 
).
 |
 |
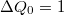| 5a. ábra Kvantum pötty elektrosztatikus energiája különböző elektronszámnál (n). A zöld pontokban az alapállapot degenerált és ezzel a pöttyön az elektron szám nem jól meghatározott. Az alapállapoti elektron számok pirossal vannak feltüntetve. | 5b. ábra Coulomb-blokád jelensége: a kvantum pöttyön keresztül csak 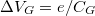 távolságra eső kapufeszültségek mellett folyik áram, mikor a pöttyön az elektron szám nem meghatározott.
|
A kapott elméleti várakozásokat vessük össze kvantum pöttyökön mért tipikus kísérleti eredményekkel. A 6. ábrán láthatóak vezetőképesség (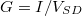
) mérések a kapufeszültség függvényében (kis 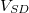mellett). Alacsony hőmérsékleten éles csúcsok jelentkeznek, amiket nulla vezetőképességű tartományok határolnak el a Coulomb-blokádnak megfelelően. A 6.a ábrán a csúcsok egyenletesen helyezkednek el 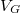tengely mentén az elektrosztatikus képben kapott eredményekkel összhangban. A hőmérséklet növelésével a csúcsok elmosódnak és a köztes völgyekben az áram egyre nagyobbra nő. Ez a termikus elmosódás akkor válik jelentőssé, ha a pötty hőmérséklete összemérhetővé válik az elektrosztatikus energiaskálával: 
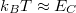. A 6.b ábrán is egy hasonló mérés látható, a Coulomb-csúcsok itt is megjelennek, ugyanakkor a csúcsok távolsága nem egyenletes, ahogyan az egyszerű modellünkből várnánk. Ennek megértéséhez már az elektrosztatikus képen túl kell lépni és a pötty bezáró potenciáljában kialakuló diszkrét elektron állapotokat figyelembe kell vennünk. Ilyen viselkedést a kisebb méretű kvantum pöttyökben tapasztalhatunk.
 |
 |
| 6a. ábra Kvantum pöttyök Coulomb-csúcsai kísérletben, | 6b. ábra Coulomb-csúcsok nem ekvidisztans poziciókban, |
| Y. Meir et al., Phys. Rev. Lett. 66, 3048 (1991). | S. Tarucha et al., Phys. Rev. Lett. 77, 3613 (1996). |
 |
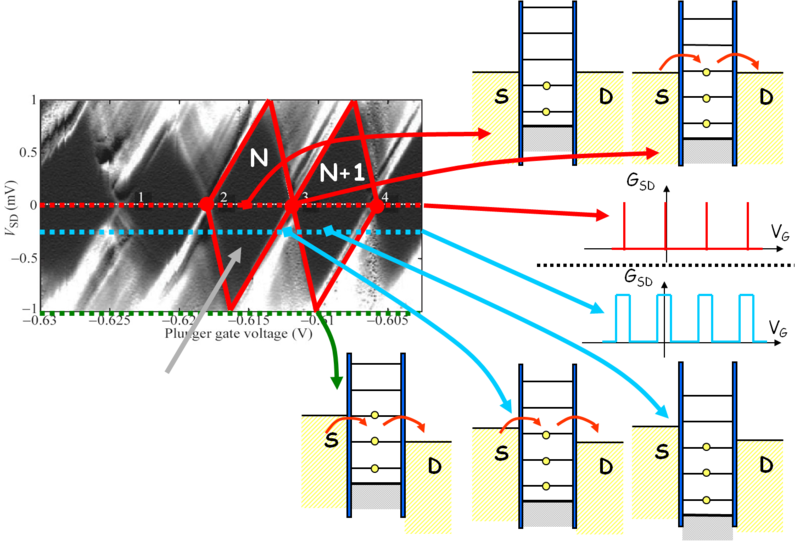
| 7. ábra Coulomb gyémánt mintázat. A kvantum pötty energiaszintjei a gyémánt mintázat különböző részein |
Szöveg egyelektron-tranzisztorrol
Összefoglalva az alfejezetet, a kvantum pöttyök viselkedését egy leegyszerűsített model keretében tárgyaltuk, ami a kvantum pöttyön az elektronok között fellépő Coulomb-taszítást vette figyelembe, ezt is egyszerű elektrosztatikus közelítésen keresztül a pötty és a környezetében található elektródák közötti kapacitások figyelembevételével. Már ebben az egyszerű elektrosztatikuis képben a kvantum pöttyök alapvető elektromos vezetési tulajdonságai, úgy mint a Coulomb-blokád jelenség vagy a Coulomb-gyémánt mintázatok megérthetőek.
S. Tarucha et al., Phys. Rev. Lett. 77, 3613 (1996).
az va. Az teszi érdekessé, hogy kontaktálható... Mesterséges atomok,
![\[<Q>=T\cdot e+(1-T)\cdot 0=T\cdot e,\]](/images/math/5/b/a/5bab70164556df83b81d56389eb1de9a.png)
tárgyalt két dimenziós elektrongázok illetve láttunk páldákat, olyan 2 illetve nanoszerkezetek előállitásáról szóló
Elektrosztatikus energia kvantum pöttyökben
Coulomb gyémántok
Mesterséges atomok és kvantum bezártság
Pauli spin blokád
Cotunneling és Kondo effektus
Kvantum pöttyök felhasználása
Egy elektron pumpa, spin kvantum bit
| |
| 1. ábra |
Az MBE olyan termikus forrásfűtésű, 0.001
| |
|
| 3a. ábra | 3b. ábra |
abban a zaj fogalmát.
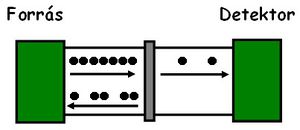
A korábbiakban láttuk, hogy egy egycsatornás kvantumvezeték vezetőképessége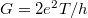 
, ahol 
a vezeték közepén elhelyezett szórócentrum transzmissziós valószínűsége. Ez a vezetőképesség abból adódik, hogy a bejövő elektronhullám parciálisan transzmittálódik illetve reflektálódik. A fotonokkal végzett kétrés kísérlethez hasonlóan ha megmérjük, hogy egy elektron áthaladt vagy visszaverődött a szórócentrumon, akkor csak azt kaphatjuk, hogy vagy az egész elektron áthaladt vagy az egész elektron visszaverődött, parciális töltés transzmisszióját nem mérhetjük. Így a mért áram (ill. vezetőképesség) abból adódik, hogy az elektronok -ed része teljesen transzmittálódik,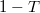 
-ed része pedig reflektálódik. Innen már rögtön látszik, hogy a véletlenszerűen transzmittálódó töltéscsomagok árama a várható érték körül fluktuálni fog.
 |
| 1. ábra |
Egy elektronra vonatkoztatva az áthaladt töltés $T$ valószínűséggel $e$, $1-T$ valószínűséggel pedig $0$, így várhatóértékben $$<Q>=T\cdot e+(1-T)\cdot 0=T\cdot e,$$ azaz a Landauer formulának megfelelően az áram $T$-vel arányos. Hasonlóan kiszámolhatjuk az áthaladt töltés szórásnégyzetét: $$<(\Delta Q)^2>=<Q^2>-<Q>^2=T\cdot e^2 - (T\cdot e)^2=T(1-T)e^2,$$ azaz az áram szórásnégyzete $T(1-T)$-vel arányos, ami $T=0$ és $T=1$ kivételével mindig véges, azaz egy részlegesen transzmittáló nanovezeték mindig véges áramfluktuációt, véges zajt mutat.
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.
</wlatex>
Az áram időbeli fluktuációja
A korábbiakban l
A zaj, azaz egy mennyiség várható érték körüli fluktuációja sok esetben lényeges többlet információt hordozhat a várható értékhez (pl. vezetőképességhez) képest, amire a későbbiekben pár egyszerű példát mutatunk. Mindenek előtt azonban definiáljuk pontosabban a zaj fogalmát.
[1] Jonathan P Bird, Electron transport in quantum dots, Kluwer Academic Publishers, (2003). [2] Jan von Delft and D. C. Ralph, Spectroscopy of Discrete Energy Levels in Ultrasmall Metallic Grains, Physics Reports 345, 61 (2001).
