„Folyadékok felületi feszültségének mérése” változatai közötti eltérés

A Fizipedia wikiből
(Új oldal, tartalma: „Folyadékok felületi feszültségének mérése A mérés célja: - megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével; - elmély…”)
 
1. sor: 1. sor:
−
Folyadékok felületi feszültségének mérése
+
<wlatex>
−
 
+
__TOC__
 
   
 
   
−
A mérés célja:
+
''A mérés célja:''
 +
 
 
- megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével;
 
- megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével;
−
- elmélyíteni a felületi feszültséggel kapcsolatos ismere-teket.
 
  
−
Ennek érdekében:
+
- elmélyíteni a felületi feszültséggel kapcsolatos ismereteket.
−
- ismertetünk néhány a felületi feszültség mérésére al-kalmas módszert;
+
−
- az ismertetett módszerek segítségével felületi feszült-séget mérünk;
+
−
- vizsgáljuk a folyadék felületi feszültségének a hőmér-séklettől és a folyadék összetételétől való függését.
+
  
−
1. Elméleti összefoglaló
 
  
−
Tapasztalati tény, hogy a folyadékfelszín igyekszik a lehető legkisebbre összehúzódni. A folyadékfelszín visel-kedését egy olyan rugalmas hártya viselkedéséhez hason-líthatjuk, amelynek határvonalán erő hat. Ennek alapján a folyadék felszínét határoló görbe bármely l darabjára a felszín érintősíkjában a vonaldarabra merőlegesen
+
''Ennek érdekében:''
  
−
  (1)
+
- ismertetünk néhány a felületi feszültség mérésére alkalmas módszert;
  
−
nagyságú erő hat. Ugyanekkora erő hat a felszín bármely belső, elemien keskeny l hosszúságú ún. vonalelemének mindkét oldalára. Az (1) kifejezésben szereplő  arányos-sági tényezőt felületi feszültségnek nevezzük:
+
- az ismertetett módszerek segítségével felületi feszültséget mérünk;
  
−
(2)
+
- vizsgáljuk a folyadék felületi feszültségének a hőmérséklettől és a folyadék összetételétől való függését.
  
−
A felületi feszültség az egységnyi vonalhosszúságra ható erő. Mértékegysége Nm-1. A felületi feszültség a folyadék-felszín növeléséhez szükséges munkával is kapcsolatba hozható. A folyadék felszínének A-val való megnövelé-séhez szükséges munka arányos a felület növekedésével és a   felületi szabadenergiával:
 
  
−
,   (3)
+
==Elméleti összefoglaló==
  
−
ahol a felületi szabadenergia mértékegysége Jm-2. Be-látható, hogy folyadékok esetében a felületi feszültség egyenlő a felületi szabadenergiával. Ezért a két mennyisé-get gyakran nem különböztetik meg. Az egyenlőség azon-ban kizárólag folyadékok esetén igaz, hiszen a szabad-energia mindig skalár, míg a felületi feszültség általában tenzor (pl. szilárdtestek esetén).
+
Tapasztalati tény, hogy a folyadékfelszín igyekszik a lehető legkisebbre összehúzódni. A folyadékfelszín viselkedését egy olyan rugalmas hártya viselkedéséhez hasonlíthatjuk, amelynek határvonalán erő hat. Ennek alapján a folyadék felszínét határoló görbe bármely &Delta;''l'' darabjára a felszín érintősíkjában a vonaldarabra merőlegesen
−
+
 
−
Az, hogy a fenti két mennyiség folyadékok esetén va-lóban egyenlő, az 1. ábrán vázolt kísérlet elemzésével lát-ható be. Az (1) összefüggés szerint a hártya egyik oldalát alkotó l hosszúságú keretdarabra
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \Delta F = \alpha \Delta l \]</latex></div>
 +
| align = "right" | <span id="eq2"> (1) </span>
 +
|}
 +
 
 +
nagyságú erő hat. Ugyanekkora erő hat a felszín bármely belső, elemien keskeny &Delta;''l'' hosszúságú ún. vonalelemének mindkét oldalára. Az (1) kifejezésben szereplő &alpha; arányossági tényezőt felületi feszültségnek nevezzük:
 +
 
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \alpha = \frac{\Delta F}{\Delta l} \]</latex></div>
 +
| align = "right" | <span id="eq2"> (2) </span>
 +
|}
 +
 
 +
A felületi feszültség az egységnyi vonalhosszúságra ható erő. Mértékegysége Nm<sup>-1</sup>. A felületi feszültség a folyadékfelszín növeléséhez szükséges munkával is kapcsolatba hozható. A folyadék felszínének &Delta;''A''-val való megnöveléséhez szükséges munka arányos a felület növekedésével és a &gamma; felületi szabadenergiával:
 +
 
 +
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \Delta W = \Delta E_f = \gamma \Delta A \]</latex></div>
 +
| align = "right" | <span id="eq2"> (3) </span>
 +
|}
 +
 
 +
ahol a felületi szabadenergia mértékegysége Jm<sup>-2</sup>. Belátható, hogy folyadékok esetében a felületi feszültség egyenlő a felületi szabadenergiával. Ezért a két mennyiséget gyakran nem különböztetik meg. Az egyenlőség azonban kizárólag folyadékok esetén igaz, hiszen a szabadenergia mindig skalár, míg a felületi feszültség általában tenzor (pl. szilárdtestek esetén).
 +
 
 +
[[Fájl:felfesz_1_abra.jpg|bélyegkép|180px|1.ábra]]
  
−
          (4)
+
Az, hogy a fenti két mennyiség folyadékok esetén valóban egyenlő, az 1. ábrán vázolt kísérlet elemzésével látható be. Az (1) összefüggés szerint a hártya egyik oldalát alkotó ''l'' hosszúságú keretdarabra
  
 +
{| width = "80%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ F_f = 2 \alpha l \]</latex></div>
 +
| align = "right" | <span id="eq2"> (4) </span>
 +
|}
 
   
 
   
−
nagyságú erő hat. (A 2-es szorzó azt veszi figyelembe, hogy a hártya első és hátsó felszínén is fellép a felületi feszültség.) Ha a keret k-val jelölt, l hosszúságú darabját x-szel elmozdítjuk, és így a hártya felszínét 2lx = A-val megnöveljük, akkor a végzett munka:
+
nagyságú erő hat. (A 2-es szorzó azt veszi figyelembe, hogy a hártya első és hátsó felszínén is fellép a felületi feszültség.) Ha a keret ''k''-val jelölt, ''l'' hosszúságú darabját &Delta;''x''-szel elmozdítjuk, és így a hártya felszínét $ 2 l \Delta x = \Delta A $-val megnöveljük, akkor a végzett munka:
  
−
      (5)
+
{| width = "80%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \Delta W = \Delta x F_h = \Delta x 2 \alpha l = \alpha \Delta A \]</latex></div>
 +
| align = "right" | <span id="eq2"> (5) </span>
 +
|}
  
−
melyet a (3) egyenlettel összevetve az = kapcsolat közvetlenül adódik. A felületi feszültség (első közelítésben) független a felszín alakjától, értéke a folya-dék minőségétől, állapotától valamint attól függ, hogy a szabad felszínnel milyen közeg érintkezik.
+
melyet a (3) egyenlettel összevetve az $ \alpha = \gamma $ kapcsolat közvetlenül adódik. A felületi feszültség (első közelítésben) független a felszín alakjától, értéke a folyadék minőségétől, állapotától valamint attól függ, hogy a szabad felszínnel milyen közeg érintkezik.
−
A táblázatokban található felületi feszültség értékek ál-talában a saját gőzével egyensúlyban lévő folyadékra vo-natkoznak. A felületi feszültség függ a hőmérséklettől, növekvő hőmérséklettel csökken és a kritikus ponton eltű-nik. Ez a viselkedés jól közelíthető az
+
A táblázatokban található felületi feszültség értékek általában a saját gőzével egyensúlyban lévő folyadékra vonatkoznak. A felületi feszültség függ a hőmérséklettől, növekvő hőmérséklettel csökken és a kritikus ponton eltűnik. Ez a viselkedés jól közelíthető az
  
−
  (6)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \alpha V^{2/3} = K \left( T_c-T \right) \]</latex></div>
 +
| align = "right" | <span id="eq2"> (6) </span>
 +
|}
  
−
Eötvös-formulával, ahol V a folyadék móltérfogata, K az Eötvös-állandó, míg Tc a kritikus hőmérséklet. Mivel a fe-lületi feszültség molekuláris erők következménye értékét erősen módosíthatja a határfelület szennyezettsége.
+
Eötvös-formulával, ahol ''V'' a folyadék móltérfogata, ''K'' az Eötvös-állandó, míg ''T<sub>c</sub>'' a kritikus hőmérséklet. Mivel a felületi feszültség molekuláris erők következménye értékét erősen módosíthatja a határfelület szennyezettsége.
  
−
2. Mérési módszerek
+
==Mérési módszerek==
  
−
2.1 Felületi feszültség mérése hajszálcső segítségével
+
===Felületi feszültség mérése hajszálcső segítségével===
  
−
Ha nagyobb szabad felületű folyadékba függőlegesen hajszálcsövet mártunk, akkor a cső belsejében a folyadék felszínének szintje a szabad felszín szintjéhez képest eltér. A csőben lévő folyadék szintje akkor magasabb, ha a fo-lyadék a cső falát nedvesíti, és akkor alacsonyabb, ha a fo-lyadék a cső falát nem nedvesíti. (2a ábra)
+
Ha nagyobb szabad felületű folyadékba függőlegesen hajszálcsövet mártunk, akkor a cső belsejében a folyadék felszínének szintje a szabad felszín szintjéhez képest eltér. A csőben lévő folyadék szintje akkor magasabb, ha a folyadék a cső falát nedvesíti, és akkor alacsonyabb, ha a folyadék a cső falát nem nedvesíti. (2a ábra)
−
A nedvesítő folyadékoknál a felületi feszültség hatásá-ra fellépő erő a felemelkedett folyadékoszlop súlyával tart egyensúlyt. Ebből levezethető, hogy:
+
  
−
  ,   (7)
+
{| cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:felfesz_2_abra.jpg|közép|600px|2.ábra]]
 +
|-
 +
| align="center"|2. ábra
 +
|}
  
−
ahol h az emelkedés magassága,  a folyadék sűrűsége, g a nehézségi gyorsulás, r a cső sugara és  a nedvesítési szög. Ideálisan nedvesítő folyadék esetén ( = 0):
+
A nedvesítő folyadékoknál a felületi feszültség hatására fellépő erő a felemelkedett folyadékoszlop súlyával tart egyensúlyt. Ebből levezethető, hogy:
  
−
.   (8)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \alpha = \frac{h \rho g r}{2 \cos \theta} \]</latex></div>
 +
| align = "right" | <span id="eq2"> (7) </span>
 +
|}
  
−
A mérésnél a csőben lévő folyadékfelszín alsó pontjának magasságát mérjük meg (hm) és az emelkedés magasságát az alábbiak szerint számítjuk.(ld. 2b és 2c ábrák)
+
ahol ''h'' az emelkedés magassága, &rho; a folyadék sűrűsége, ''g'' a nehézségi gyorsulás, ''r'' a cső sugara és &theta; a nedvesítési szög. Ideálisan nedvesítő folyadék esetén (&theta; = 0):
  
−
.   (9)
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \alpha = h \rho g r / 2 \]</latex></div>
 +
| align = "right" | <span id="eq2"> (8) </span>
 +
|}
  
−
A nedvesítési szög ismeretében tehát a felületi feszültség egy kapilláris, valamint a (7) és (9) kifejezések segítségé-vel határozható meg.
+
A mérésnél a csőben lévő folyadékfelszín alsó pontjának magasságát mérjük meg (''h<sub>m</sub>'') és az emelkedés magasságát az alábbiak szerint számítjuk.(ld. 2b és 2c ábrák)
  
−
3.2 Felületi feszültség mérése csepegtetéssel
+
{| width = "100%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ h = h_m + r/3 \]</latex></div>
 +
| align = "right" | <span id="eq2"> (9) </span>
 +
|}
  
−
+
A nedvesítési szög ismeretében tehát a felületi feszültség egy kapilláris, valamint a (7) és (9) kifejezések segítségével határozható meg.
−
Ezen mérési módszer alapgondolata az, hogy egy folyadékcsepp lecseppenése akkor következik be, amikor a csepp súlya meghaladja a leszakadási felületnél a felületi feszültségből származó erőt. Ha vastag falú, függőleges, alul síkra csiszolt kapilláris csőből lassan csepegtetjük ki a csövet jól nedvesítő folyadékot, akkor a csepp felszíne az r külső sugarú csővel 2r hosszú darabon érintkezik. Ekkor a felületi feszültségből származó erő legfeljebb G = 2r  súlyú cseppet tud megtartani. Valójában a leszakadó csepp súlya a 3. ábrán látható "befűződés" mi-att a fenti értéknél kisebb: G = kr, ahol a k állandó a fe-lületi fesztültségtől, a cső méretétől és a folyadék sűrűsé-gétől függő állandó, értéke 3,8 és 4,5 közötti.
+
−
Egy adott eszköz k értékét ismert felületi feszültségű anyagok segítségével határozhatjuk meg. Tájékozódó jel-legű összehasonlító méréseknél a k ismerete mellőzhető, mert ebben az esetben két folyadékra nézve
+
  
−
. (10)
+
===Felületi feszültség mérése csepegtetéssel===
  
−
A csepegtetéssel működő felületi feszültség mérő eszkö-zöket sztalagmométereknek nevezzük.
+
[[Fájl:felfesz_3_abra.jpg|bélyegkép|120px|3. ábra]]
  
−
3.3 Felületi feszültség mérés szakításos módszerrel
+
Ezen mérési módszer alapgondolata az, hogy egy folyadékcsepp lecseppenése akkor következik be, amikor a csepp súlya meghaladja a leszakadási felületnél a felületi feszültségből származó erőt. Ha vastag falú, függőleges, alul síkra csiszolt kapilláris csőből lassan csepegtetjük ki a csövet jól nedvesítő folyadékot, akkor a csepp felszíne az ''r'' külső sugarú csővel $ 2 r \pi $ hosszú darabon érintkezik. Ekkor a felületi feszültségből származó erő legfeljebb $ G = 2 r \pi \alpha $ súlyú cseppet tud megtartani. Valójában a leszakadó csepp súlya a 3. ábrán látható "befűződés" miatt a fenti értéknél kisebb: $ G = k r \alpha $, ahol a ''k'' állandó a felületi feszültségtől, a cső méretétől és a folyadék sűrűségétől függő állandó, értéke 3,8 és 4,5 közötti.
 +
Egy adott eszköz ''k'' értékét ismert felületi feszültségű anyagok segítségével határozhatjuk meg. Tájékozódó jellegű összehasonlító méréseknél a ''k'' ismerete mellőzhető, mert ebben az esetben két folyadékra nézve
 +
 
 +
{| width = "86%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ \alpha_1 / \alpha_2 = G_1 / G_2 \]</latex></div>
 +
| align = "right" | <span id="eq2"> (10) </span>
 +
|}
 +
 
 +
A csepegtetéssel működő felületi feszültség mérő eszközöket sztalagmométereknek nevezzük.
 +
 
 +
===Felületi feszültség mérés szakításos módszerrel===
  
 
   
 
   
−
Egy folyadékba mártott gyűrűt – amelynek anyagát a folyadék nedvesíti – lassan, függőlegesen kiemeljük a fo-lyadékból, és közben folyamatosan mérjük az erőt. (4. áb-ra). Az erő maximális értéke a gyűrű súlyával és a gyűrű-höz tapadó vékony folyadékhártya elszakításához szüksé-ges erővel egyenlő.
+
Egy folyadékba mártott gyűrűt – amelynek anyagát a folyadék nedvesíti – lassan, függőlegesen kiemeljük a folyadékból, és közben folyamatosan mérjük az erőt. (4. ábra) Az erő maximális értéke a gyűrű súlyával és a gyűrűhöz tapadó vékony folyadékhártya elszakításához szükséges erővel egyenlő.
 +
 
 +
{|  cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
| [[Fájl:felfesz_4_abra.jpg|közép|640px|4.ábra]]
 +
|-
 +
| align="center"|4. ábra
 +
|}
 +
 
 
A 4a ábrán látható elrendezés esetén:
 
A 4a ábrán látható elrendezés esetén:
  
−
, (11)
+
{| width = "84%"
 +
|-
 +
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ F_{max} = G + 2 \pi \left( r_1 + r_2 \right) \alpha \]</latex></div>
 +
| align = "right" | <span id="eq2"> (11) </span>
 +
|}
  
 
a 4b ábrán látható elrendezés esetén pedig
 
a 4b ábrán látható elrendezés esetén pedig
  
−
. (12)
+
{| width = "84%"
−
 
+
|-
−
Mérési feladatok:
+
| width = "10%" |
 +
| width = "80%" | <div class="texdisplay"><latex display >\[ F_{max} = G + 4 \pi r \alpha \]</latex></div>
 +
| align = "right" | <span id="eq2"> (12) </span>
 +
|}
  
−
I. Víz-alkohol oldatok felületi feszültségének mérése csepegteté-ses módszerrel
+
==Mérési feladatok==
  
−
1. Határozzuk meg a sztalagmométer k készülékállandóját desztillált víz segítségével!
+
===Víz-alkohol oldatok felületi feszültségének mérése csepegtetéses módszerrel===
−
A sztalagmométer egy csapos tölcsér. Ne érintsük kézzel a kapilláris zsírtalanított alsó peremét ill. a tölcsér belsejét! A sztalagmométert függőleges helyzetbe rögzítjük, majd a csap elzárása után a tölcsér feléig megtöltjük desztillált vízzel. A csepegtetés megkezdése előtt mérjünk le táramérleggel egy üres műanyag edényt, majd csepegtessünk a pohárba mini-málisan 100 cseppet. A csap óvatos nyitásával a folyadék-áramlást úgy szabályozzuk be, hogy a cseppek kényelmesen számolhatóak legyenek. Az edény visszamérése után 1 csepp átlagtömege, m számolható. Az egyensúly feltételéből gm = kr, ami alapján a desztillált víz felületi feszültségé-nek ismeretében a k készülékállandó meghatározható.
+
  
−
2. Ismételjük meg az 1. feladatot 10 és 20 %-os alkohol oldat-tal! Az oldatcseréhez engedjük le a tölcséres csepegtetőből a folyadékot, töltsük fel a következő oldattal, majd azt is fo-lyassuk ki. Egy újabb (második) feltöltés után az új oldat már mérhető. Az alkoholos oldatok maradékait kérjük a gyűjtőedénybe önteni.
+
1. Határozzuk meg a sztalagmométer ''k'' készülékállandóját desztillált víz segítségével!
 +
A sztalagmométer egy csapos tölcsér. Ne érintsük kézzel a kapilláris zsírtalanított alsó peremét ill. a tölcsér belsejét! A sztalagmométert függőleges helyzetbe rögzítjük, majd a csap elzárása után a tölcsér feléig megtöltjük desztillált vízzel. A csepegtetés megkezdése előtt mérjünk le táramérleggel egy üres műanyag edényt, majd csepegtessünk a pohárba minimálisan 100 cseppet. A csap óvatos nyitásával a folyadékáramlást úgy szabályozzuk be, hogy a cseppek kényelmesen számolhatóak legyenek. Az edény visszamérése után 1 csepp átlagtömege, &Delta;''m'' számolható. Az egyensúly feltételéből $ g \Delta m = k r \alpha $, ami alapján a desztillált víz felületi feszültségének ismeretében a ''k'' készülékállandó meghatározható.
  
−
II. Szakításos felületi feszültség mérő beállítása és kalibrálása
+
2. Ismételjük meg az 1. feladatot 10 és 20 %-os alkohol oldattal! Az oldatcseréhez engedjük le a tölcséres csepegtetőből a folyadékot, töltsük fel a következő oldattal, majd azt is folyassuk ki. Egy újabb (második) feltöltés után az új oldat már mérhető. Az alkoholos oldatok maradékait kérjük a gyűjtőedénybe önteni.
  
−
3. Állítsuk össze a szakításos felületi feszültség mérőt! Az in-duktív erőmérő elektronikája az erőhatással arányos -10 és +10 V közötti feszültségjelet generál, melynek a nulla szintje potméterrel szabályozható. Ezt a feszültségjelet kös-sük a HAMEG digitális multiméterre. A mért feszültséget számítógépes interfészen keresztül, a felfesz_meres.exe program segítségével rögzítjük. Ellenőrizzük a program működését, és állítsuk be az induktív erőmérő nullszintjét  -6 V és -3 V közötti értékre. Figyelem! A mérőkeretet elő-zetesen zsírtalanítottuk, ezért azt kézzel érinteni tilos!
+
===Szakításos felületi feszültség mérő beállítása és kalibrálása===
  
−
4. Kalibráljuk az induktív erőmérőt! Akasszunk növekvő számban felfüggeszthető súlyokat az erőmérőre, és a súlyok számának függvényében vegyük fel az erőmérő kimenő fe-szültségét, illesszünk egyenest a mért pontokra. (Megj.: a súlyokat ne a mérőkeretre, hanem a mérőkeret feletti mű-anyag lapon található lyukakba akasszuk. Ügyeljünk a keret egyenletes terhelésére, ha a súlyok egy oldalra húzzák a ke-retet, megnő az induktív erőmérőben a súrlódás, ami növeli a mérési hibát. A súlyok átlagos tömege: 0,47 g)
+
3. Állítsuk össze a szakításos felületi feszültség mérőt! Az induktív erőmérő elektronikája az erőhatással arányos -10 és +10 V közötti feszültségjelet generál, melynek a nulla szintje potméterrel szabályozható. Ezt a feszültségjelet kössük a HAMEG digitális multiméterre. A mért feszültséget számítógépes interfészen keresztül, a felfesz_meres.exe program segítségével rögzítjük. Ellenőrizzük a program működését, és állítsuk be az induktív erőmérő nullszintjét  -6 V és -3 V közötti értékre. Figyelem! A mérőkeretet előzetesen zsírtalanítottuk, ezért azt kézzel érinteni tilos!
  
−
5. Vízszintezzük a mérőkeretet! Ehhez helyezzünk a keret alá egy állítható lábú plexi asztalkát. Az asztalra helyezett víz-szintmérő segítségével vízszintezzük az aszalt olyan ma-gasságban, hogy a mérőkeret éppen ne érjen hozzá. Ezután a mérőkeret feletti műanyag tárcsán található piros csava-rok segítségével állítsuk be a mérőkeretet az asztal síkjával párhuzamosan. A mérőkeret vízszintességét a mérés során többször is ellenőrizzük, és szükség esetén korrigáljuk.  
+
4. Kalibráljuk az induktív erőmérőt! Akasszunk növekvő számban felfüggeszthető súlyokat az erőmérőre, és a súlyok számának függvényében vegyük fel az erőmérő kimenő feszültségét, illesszünk egyenest a mért pontokra. (Megj.: a súlyokat ne a mérőkeretre, hanem a mérőkeret feletti műanyag lapon található lyukakba akasszuk. Ügyeljünk a keret egyenletes terhelésére, ha a súlyok egy oldalra húzzák a keretet, megnő az induktív erőmérőben a súrlódás, ami növeli a mérési hibát. A súlyok átlagos tömege: 0,47 g)
  
 +
5. Vízszintezzük a mérőkeretet! Ehhez helyezzünk a keret alá egy állítható lábú plexi asztalkát. Az asztalra helyezett vízszintmérő segítségével vízszintezzük az aszalt olyan magasságban, hogy a mérőkeret éppen ne érjen hozzá. Ezután a mérőkeret feletti műanyag tárcsán található piros csavarok segítségével állítsuk be a mérőkeretet az asztal síkjával párhuzamosan. A mérőkeret vízszintességét a mérés során többször is ellenőrizzük, és szükség esetén korrigáljuk.
 
   
 
   
−
III. Víz-alkohol oldatok felületi feszültségének mérése szakítá-sos módszerrel
+
===Víz-alkohol oldatok felületi feszültségének mérése szakításos módszerrel===
  
−
6. Helyezzük a deszt. víz feliratú, leeresztő csappal ellátott edényt a mérőkeret alá. Töltsük fel az edényt desztillált víz-zel addig, hogy a vízszint pár mm magasan legyen a keret alsó éle felett. Gyors csepegtetéssel eresszük le az edényből a vizet a deszt. víz feliratú gyűjtőedénybe, közben vegyük fel az erő változását a gyűrű szakadásáig. Ekkor a csapot elzárva a pohárból töltsük vissza a vizet a keret közepébe (nem a keretre!) és a szakítási kísérletet ismételjük meg legalább kétszer! (Megj.: az erőt mindig az elszakadás előtti és a szakadás utáni feszültségszint különbségéből állapítsuk meg. A mérőkeret átmérője a szakítási élnél: 91 mm)  
+
6. Helyezzük a deszt. víz feliratú, leeresztő csappal ellátott edényt a mérőkeret alá. Töltsük fel az edényt desztillált vízzel addig, hogy a vízszint pár mm magasan legyen a keret alsó éle felett. Gyors csepegtetéssel eresszük le az edényből a vizet a deszt. víz feliratú gyűjtőedénybe, közben vegyük fel az erő változását a gyűrű szakadásáig. Ekkor a csapot elzárva a pohárból töltsük vissza a vizet a keret közepébe (nem a keretre!) és a szakítási kísérletet ismételjük meg legalább kétszer! (Megj.: az erőt mindig az elszakadás előtti és a szakadás utáni feszültségszint különbségéből állapítsuk meg. A mérőkeret átmérője a szakítási élnél: 91 mm)  
  
−
7. A 6. mérést ismételjük meg 10 %-os és 20 %-os alkoholol-dattal. Figyelem! Az oldatokat mindig a koncentrációnak megfelelő feliratú edénybe töltsük, majd a mérés végén ne öntsük ki, hanem töltsük vissza a megfelelő tároló edénybe. Ügyeljünk rá, hogy az oldatok ne keveredjenek.
+
7. A 6. mérést ismételjük meg 10 %-os és 20 %-os alkohololdattal. Figyelem! Az oldatokat mindig a koncentrációnak megfelelő feliratú edénybe töltsük, majd a mérés végén ne öntsük ki, hanem töltsük vissza a megfelelő tároló edénybe. Ügyeljünk rá, hogy az oldatok ne keveredjenek.
  
−
IV. Desztillált víz felületi feszültségének hőmérséklet függése, Eötvös-féle szabály igazolása
+
===Desztillált víz felületi feszültségének hőmérséklet függése, Eötvös-féle szabály igazolása===
  
−
8. A 6. mérést ismételjük meg desztillált vízzel 40 és 60 °C-os hőmérsékleten. Hőmérséklet méréséhez rögzítsük a higany-szálas hőmérőt a bunsen állványhoz. A víz melegítése köz-ben használjunk mágneses keverőt, de az erőmérés előtt kapcsoljuk ki a keverőt, és várjuk meg, míg a vízfelszín megnyugszik.
+
8. A 6. mérést ismételjük meg desztillált vízzel 40 és 60 °C-os hőmérsékleten. Hőmérséklet méréséhez rögzítsük a higanyszálas hőmérőt a bunsen állványhoz. A víz melegítése közben használjunk mágneses keverőt, de az erőmérés előtt kapcsoljuk ki a keverőt, és várjuk meg, míg a vízfelszín megnyugszik.
−
Ábrázoljuk a felületi feszültséget a hőmérséklet függvényé-ben, és illesszünk egyenest a mérési pontokra! Az egyenes paramétereiből határozzuk meg az Eötvös-állandót és a kri-tikus hőmérsékletet.
+
Ábrázoljuk a felületi feszültséget a hőmérséklet függvényében, és illesszünk egyenest a mérési pontokra! Az egyenes paramétereiből határozzuk meg az Eötvös-állandót és a kritikus hőmérsékletet.

A lap 2012. január 31., 21:32-kori változata


Tartalomjegyzék


A mérés célja:

- megismerkedni a folyadékok felületi feszültségének néhány mérési módszerével;

- elmélyíteni a felületi feszültséggel kapcsolatos ismereteket.


Ennek érdekében:

- ismertetünk néhány a felületi feszültség mérésére alkalmas módszert;

- az ismertetett módszerek segítségével felületi feszültséget mérünk;

- vizsgáljuk a folyadék felületi feszültségének a hőmérséklettől és a folyadék összetételétől való függését.


Elméleti összefoglaló

Tapasztalati tény, hogy a folyadékfelszín igyekszik a lehető legkisebbre összehúzódni. A folyadékfelszín viselkedését egy olyan rugalmas hártya viselkedéséhez hasonlíthatjuk, amelynek határvonalán erő hat. Ennek alapján a folyadék felszínét határoló görbe bármely Δl darabjára a felszín érintősíkjában a vonaldarabra merőlegesen

\[ \Delta F = \alpha \Delta l \]
 (1)

nagyságú erő hat. Ugyanekkora erő hat a felszín bármely belső, elemien keskeny Δl hosszúságú ún. vonalelemének mindkét oldalára. Az (1) kifejezésben szereplő α arányossági tényezőt felületi feszültségnek nevezzük:

\[ \alpha = \frac{\Delta F}{\Delta l} \]
 (2)

A felületi feszültség az egységnyi vonalhosszúságra ható erő. Mértékegysége Nm-1. A felületi feszültség a folyadékfelszín növeléséhez szükséges munkával is kapcsolatba hozható. A folyadék felszínének ΔA-val való megnöveléséhez szükséges munka arányos a felület növekedésével és a γ felületi szabadenergiával:

\[ \Delta W = \Delta E_f = \gamma \Delta A \]
 (3)

ahol a felületi szabadenergia mértékegysége Jm-2. Belátható, hogy folyadékok esetében a felületi feszültség egyenlő a felületi szabadenergiával. Ezért a két mennyiséget gyakran nem különböztetik meg. Az egyenlőség azonban kizárólag folyadékok esetén igaz, hiszen a szabadenergia mindig skalár, míg a felületi feszültség általában tenzor (pl. szilárdtestek esetén).

1.ábra

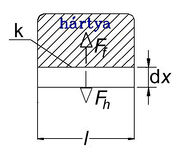
Az, hogy a fenti két mennyiség folyadékok esetén valóban egyenlő, az 1. ábrán vázolt kísérlet elemzésével látható be. Az (1) összefüggés szerint a hártya egyik oldalát alkotó l hosszúságú keretdarabra

\[ F_f = 2 \alpha l \]
 (4)

nagyságú erő hat. (A 2-es szorzó azt veszi figyelembe, hogy a hártya első és hátsó felszínén is fellép a felületi feszültség.) Ha a keret k-val jelölt, l hosszúságú darabját Δx-szel elmozdítjuk, és így a hártya felszínét 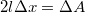\setbox0\hbox{$ 2 l \Delta x = \Delta A $}% \message{//depth:\the\dp0//}% \box0%-val megnöveljük, akkor a végzett munka:

\[ \Delta W = \Delta x F_h = \Delta x 2 \alpha l = \alpha \Delta A \]
 (5)

melyet a (3) egyenlettel összevetve az 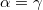\setbox0\hbox{$ \alpha = \gamma $}% \message{//depth:\the\dp0//}% \box0% kapcsolat közvetlenül adódik. A felületi feszültség (első közelítésben) független a felszín alakjától, értéke a folyadék minőségétől, állapotától valamint attól függ, hogy a szabad felszínnel milyen közeg érintkezik. A táblázatokban található felületi feszültség értékek általában a saját gőzével egyensúlyban lévő folyadékra vonatkoznak. A felületi feszültség függ a hőmérséklettől, növekvő hőmérséklettel csökken és a kritikus ponton eltűnik. Ez a viselkedés jól közelíthető az

\[ \alpha V^{2/3} = K \left( T_c-T \right) \]
 (6)

Eötvös-formulával, ahol V a folyadék móltérfogata, K az Eötvös-állandó, míg Tc a kritikus hőmérséklet. Mivel a felületi feszültség molekuláris erők következménye értékét erősen módosíthatja a határfelület szennyezettsége.

Mérési módszerek

Felületi feszültség mérése hajszálcső segítségével

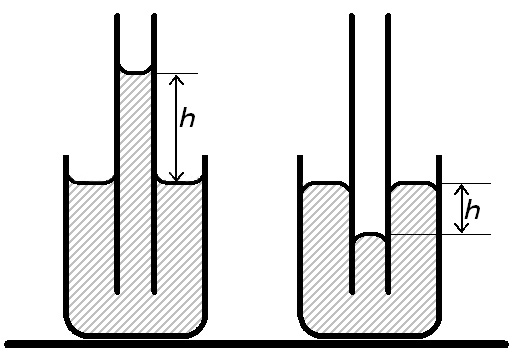
Ha nagyobb szabad felületű folyadékba függőlegesen hajszálcsövet mártunk, akkor a cső belsejében a folyadék felszínének szintje a szabad felszín szintjéhez képest eltér. A csőben lévő folyadék szintje akkor magasabb, ha a folyadék a cső falát nedvesíti, és akkor alacsonyabb, ha a folyadék a cső falát nem nedvesíti. (2a ábra)

2.ábra
2. ábra

A nedvesítő folyadékoknál a felületi feszültség hatására fellépő erő a felemelkedett folyadékoszlop súlyával tart egyensúlyt. Ebből levezethető, hogy:

\[ \alpha = \frac{h \rho g r}{2 \cos \theta} \]
 (7)

ahol h az emelkedés magassága, ρ a folyadék sűrűsége, g a nehézségi gyorsulás, r a cső sugara és θ a nedvesítési szög. Ideálisan nedvesítő folyadék esetén (θ = 0):

\[ \alpha = h \rho g r / 2 \]
 (8)

A mérésnél a csőben lévő folyadékfelszín alsó pontjának magasságát mérjük meg (hm) és az emelkedés magasságát az alábbiak szerint számítjuk.(ld. 2b és 2c ábrák)

\[ h = h_m + r/3 \]
 (9)

A nedvesítési szög ismeretében tehát a felületi feszültség egy kapilláris, valamint a (7) és (9) kifejezések segítségével határozható meg.

Felületi feszültség mérése csepegtetéssel

3. ábra

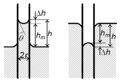
Ezen mérési módszer alapgondolata az, hogy egy folyadékcsepp lecseppenése akkor következik be, amikor a csepp súlya meghaladja a leszakadási felületnél a felületi feszültségből származó erőt. Ha vastag falú, függőleges, alul síkra csiszolt kapilláris csőből lassan csepegtetjük ki a csövet jól nedvesítő folyadékot, akkor a csepp felszíne az r külső sugarú csővel 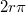\setbox0\hbox{$ 2 r \pi $}% \message{//depth:\the\dp0//}% \box0% hosszú darabon érintkezik. Ekkor a felületi feszültségből származó erő legfeljebb 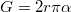\setbox0\hbox{$ G = 2 r \pi \alpha $}% \message{//depth:\the\dp0//}% \box0% súlyú cseppet tud megtartani. Valójában a leszakadó csepp súlya a 3. ábrán látható "befűződés" miatt a fenti értéknél kisebb: 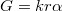\setbox0\hbox{$ G = k r \alpha $}% \message{//depth:\the\dp0//}% \box0%, ahol a k állandó a felületi feszültségtől, a cső méretétől és a folyadék sűrűségétől függő állandó, értéke 3,8 és 4,5 közötti. Egy adott eszköz k értékét ismert felületi feszültségű anyagok segítségével határozhatjuk meg. Tájékozódó jellegű összehasonlító méréseknél a k ismerete mellőzhető, mert ebben az esetben két folyadékra nézve

\[ \alpha_1 / \alpha_2 = G_1 / G_2 \]
 (10)

A csepegtetéssel működő felületi feszültség mérő eszközöket sztalagmométereknek nevezzük.

Felületi feszültség mérés szakításos módszerrel

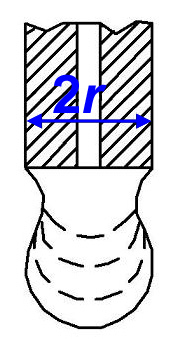
Egy folyadékba mártott gyűrűt – amelynek anyagát a folyadék nedvesíti – lassan, függőlegesen kiemeljük a folyadékból, és közben folyamatosan mérjük az erőt. (4. ábra) Az erő maximális értéke a gyűrű súlyával és a gyűrűhöz tapadó vékony folyadékhártya elszakításához szükséges erővel egyenlő.

4.ábra
4. ábra

A 4a ábrán látható elrendezés esetén:

\[ F_{max} = G + 2 \pi \left( r_1 + r_2 \right) \alpha \]
 (11)

a 4b ábrán látható elrendezés esetén pedig

\[ F_{max} = G + 4 \pi r \alpha \]
 (12)

Mérési feladatok

Víz-alkohol oldatok felületi feszültségének mérése csepegtetéses módszerrel

1. Határozzuk meg a sztalagmométer k készülékállandóját desztillált víz segítségével! A sztalagmométer egy csapos tölcsér. Ne érintsük kézzel a kapilláris zsírtalanított alsó peremét ill. a tölcsér belsejét! A sztalagmométert függőleges helyzetbe rögzítjük, majd a csap elzárása után a tölcsér feléig megtöltjük desztillált vízzel. A csepegtetés megkezdése előtt mérjünk le táramérleggel egy üres műanyag edényt, majd csepegtessünk a pohárba minimálisan 100 cseppet. A csap óvatos nyitásával a folyadékáramlást úgy szabályozzuk be, hogy a cseppek kényelmesen számolhatóak legyenek. Az edény visszamérése után 1 csepp átlagtömege, Δm számolható. Az egyensúly feltételéből 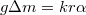\setbox0\hbox{$ g \Delta m = k r \alpha $}% \message{//depth:\the\dp0//}% \box0%, ami alapján a desztillált víz felületi feszültségének ismeretében a k készülékállandó meghatározható.

2. Ismételjük meg az 1. feladatot 10 és 20 %-os alkohol oldattal! Az oldatcseréhez engedjük le a tölcséres csepegtetőből a folyadékot, töltsük fel a következő oldattal, majd azt is folyassuk ki. Egy újabb (második) feltöltés után az új oldat már mérhető. Az alkoholos oldatok maradékait kérjük a gyűjtőedénybe önteni.

Szakításos felületi feszültség mérő beállítása és kalibrálása

3. Állítsuk össze a szakításos felületi feszültség mérőt! Az induktív erőmérő elektronikája az erőhatással arányos -10 és +10 V közötti feszültségjelet generál, melynek a nulla szintje potméterrel szabályozható. Ezt a feszültségjelet kössük a HAMEG digitális multiméterre. A mért feszültséget számítógépes interfészen keresztül, a felfesz_meres.exe program segítségével rögzítjük. Ellenőrizzük a program működését, és állítsuk be az induktív erőmérő nullszintjét -6 V és -3 V közötti értékre. Figyelem! A mérőkeretet előzetesen zsírtalanítottuk, ezért azt kézzel érinteni tilos!

4. Kalibráljuk az induktív erőmérőt! Akasszunk növekvő számban felfüggeszthető súlyokat az erőmérőre, és a súlyok számának függvényében vegyük fel az erőmérő kimenő feszültségét, illesszünk egyenest a mért pontokra. (Megj.: a súlyokat ne a mérőkeretre, hanem a mérőkeret feletti műanyag lapon található lyukakba akasszuk. Ügyeljünk a keret egyenletes terhelésére, ha a súlyok egy oldalra húzzák a keretet, megnő az induktív erőmérőben a súrlódás, ami növeli a mérési hibát. A súlyok átlagos tömege: 0,47 g)

5. Vízszintezzük a mérőkeretet! Ehhez helyezzünk a keret alá egy állítható lábú plexi asztalkát. Az asztalra helyezett vízszintmérő segítségével vízszintezzük az aszalt olyan magasságban, hogy a mérőkeret éppen ne érjen hozzá. Ezután a mérőkeret feletti műanyag tárcsán található piros csavarok segítségével állítsuk be a mérőkeretet az asztal síkjával párhuzamosan. A mérőkeret vízszintességét a mérés során többször is ellenőrizzük, és szükség esetén korrigáljuk.

Víz-alkohol oldatok felületi feszültségének mérése szakításos módszerrel

6. Helyezzük a deszt. víz feliratú, leeresztő csappal ellátott edényt a mérőkeret alá. Töltsük fel az edényt desztillált vízzel addig, hogy a vízszint pár mm magasan legyen a keret alsó éle felett. Gyors csepegtetéssel eresszük le az edényből a vizet a deszt. víz feliratú gyűjtőedénybe, közben vegyük fel az erő változását a gyűrű szakadásáig. Ekkor a csapot elzárva a pohárból töltsük vissza a vizet a keret közepébe (nem a keretre!) és a szakítási kísérletet ismételjük meg legalább kétszer! (Megj.: az erőt mindig az elszakadás előtti és a szakadás utáni feszültségszint különbségéből állapítsuk meg. A mérőkeret átmérője a szakítási élnél: 91 mm)

7. A 6. mérést ismételjük meg 10 %-os és 20 %-os alkohololdattal. Figyelem! Az oldatokat mindig a koncentrációnak megfelelő feliratú edénybe töltsük, majd a mérés végén ne öntsük ki, hanem töltsük vissza a megfelelő tároló edénybe. Ügyeljünk rá, hogy az oldatok ne keveredjenek.

Desztillált víz felületi feszültségének hőmérséklet függése, Eötvös-féle szabály igazolása

8. A 6. mérést ismételjük meg desztillált vízzel 40 és 60 °C-os hőmérsékleten. Hőmérséklet méréséhez rögzítsük a higanyszálas hőmérőt a bunsen állványhoz. A víz melegítése közben használjunk mágneses keverőt, de az erőmérés előtt kapcsoljuk ki a keverőt, és várjuk meg, míg a vízfelszín megnyugszik. Ábrázoljuk a felületi feszültséget a hőmérséklet függvényében, és illesszünk egyenest a mérési pontokra! Az egyenes paramétereiből határozzuk meg az Eötvös-állandót és a kritikus hőmérsékletet.

A lap eredeti címe: „https://fizipedia.bme.hu/index.php?title=Folyadékok_felületi_feszültségének_mérése&oldid=2515”