„Állóhullámok megfeszített, rugalmas húrban” változatai közötti eltérés
| 26. sor: | 26. sor: | ||
* megvizsgáljuk egy mindkét végén rögzített húrban ki-alakuló állóhullámokat, | * megvizsgáljuk egy mindkét végén rögzített húrban ki-alakuló állóhullámokat, | ||
* hullámhossz- és frekvenciamérésekkel meghatározzuk a húrban a hang terjedési sebességét, és annak függését a húr jellemző adataitól. | * hullámhossz- és frekvenciamérésekkel meghatározzuk a húrban a hang terjedési sebességét, és annak függését a húr jellemző adataitól. | ||
| + | |||
__TOC__ | __TOC__ | ||
| 33. sor: | 34. sor: | ||
Kísérleteink során mindkét végén rögzített húrban terjedő hullámokat vizsgálunk. A hullám leírásánál feltételezzük, hogy a hullámterjedés egydimenziósnak tekinthető (a hullám a húr mentén terjed), a hullám transzverzális (a húr pontjainak elmozdulásvektorai a húrra merőlegesek) és síkban polarizált (a pontok elmozdulásvektorai mindig ugyanabban a síkban vannak). Ez azt jelenti, hogy a húr pontjainak az egyensúlyi helyzetből való kitérése (elmozdulása) egyetlen skaláris mennyiséggel jellemezhető. A hullám leírására a fentiek alapján a húrral párhuzamosan választott $x$-tengely esetén a | Kísérleteink során mindkét végén rögzített húrban terjedő hullámokat vizsgálunk. A hullám leírásánál feltételezzük, hogy a hullámterjedés egydimenziósnak tekinthető (a hullám a húr mentén terjed), a hullám transzverzális (a húr pontjainak elmozdulásvektorai a húrra merőlegesek) és síkban polarizált (a pontok elmozdulásvektorai mindig ugyanabban a síkban vannak). Ez azt jelenti, hogy a húr pontjainak az egyensúlyi helyzetből való kitérése (elmozdulása) egyetlen skaláris mennyiséggel jellemezhető. A hullám leírására a fentiek alapján a húrral párhuzamosan választott $x$-tengely esetén a | ||
{{eq|c^2\frac{\partial^2\psi(x,t)}{\partial x^2}{{=}}\frac{\partial^2\psi(x,t)}{\partial t^2}|eq:1|(1)}} | {{eq|c^2\frac{\partial^2\psi(x,t)}{\partial x^2}{{=}}\frac{\partial^2\psi(x,t)}{\partial t^2}|eq:1|(1)}} | ||
| − | egydimenziós hullámegyenletet használhatjuk. Itt $x$ koordináta, $t$ az idő, a kitérés hely- és időfüggését megadó | + | egydimenziós hullámegyenletet használhatjuk. Itt $x$ koordináta, $t$ az idő, a kitérés hely- és időfüggését megadó – tehát a hullám terjedését leíró – hullámfüggvény, $c$ pedig a hullám terjedési sebessége a húron. Ha a hullámegyenletet a húr esetére levezetjük, akkor kiderül, hogy a $c$ terjedési sebessége a húrt megfeszítő erőtől $(T)$ és a húr egységnyi hosszára jutó tömegtől $(\mu)$ függ, és ezekkel az alábbi módon fejezhető ki |
{{eq|c{{=}}\sqrt{\frac{T}{\mu} }.|eq:2|(2)}} | {{eq|c{{=}}\sqrt{\frac{T}{\mu} }.|eq:2|(2)}} | ||
| − | A húrban valamilyen külső gerjesztés hatására kialakuló hullám általában igen bonyolult. Tapasztalatból tudjuk azonban, hogy meghatározott frekvenciákon történő gerjesztés esetén a húron, a végekről visszaverődő hullámok interferenciája révén sajátos, állandósult hullámalakzat | + | A húrban valamilyen külső gerjesztés hatására kialakuló hullám általában igen bonyolult. Tapasztalatból tudjuk azonban, hogy meghatározott frekvenciákon történő gerjesztés esetén a húron, a végekről visszaverődő hullámok interferenciája révén sajátos, állandósult hullámalakzat – ún. állóhullám – jön létre. Ennek jellegzetessége az, hogy a húr meghatározott szakaszán levő pontok azonos fázisban rezegnek, a rezgés amplitúdója pedig a hely függvénye. Ez matematikailag úgy fogalmazható meg, hogy az [[#eq:1|(1)]] egyenletnek létezik olyan megoldása, amely egy csak helytől és egy csak időtől függő függvény szorzata [az [[#eq:1|(1)]] parciális differenciálegyenletben a változók szeparálhatók]. Harmonikus gerjesztés esetén ez a megoldás a |
{{eq|\psi(x,t){{=}}\varphi(x)\sin(\omega t+\alpha)|eq:3|(3)}} | {{eq|\psi(x,t){{=}}\varphi(x)\sin(\omega t+\alpha)|eq:3|(3)}} | ||
alakban írható fel, ahol $\omega=2\pi\nu$ a rezgés körfrekvenciája ($\nu$ frekvencia, Hz), $\alpha$ pedig a fázisszög. | alakban írható fel, ahol $\omega=2\pi\nu$ a rezgés körfrekvenciája ($\nu$ frekvencia, Hz), $\alpha$ pedig a fázisszög. | ||
| − | A [[#eq:3|(3)]] megoldást az [[#eq:1|(1)]] egyenletbe helyettesítve az időfüggő rész kiesik, a helyfüggő részre pedig | + | A [[#eq:3|(3)]] megoldást az [[#eq:1|(1)]] egyenletbe helyettesítve az időfüggő rész kiesik, a helyfüggő részre pedig – amely a rezgés amplitúdójának a húr mentén való változását adja meg – az alábbi közönséges másodrendű differenciál-egyenletet eredményezi: |
{{eq|\frac{\mathrm{d}^2\varphi(x)}{\mathrm{d}x^2}+k^2\varphi(x){{=}}0.|eq:4|(4)}} | {{eq|\frac{\mathrm{d}^2\varphi(x)}{\mathrm{d}x^2}+k^2\varphi(x){{=}}0.|eq:4|(4)}} | ||
Az egyenletben bevezettük a $k$ hullámszámot, amelyet a $k=\frac{\omega}{c}$ összefüggés definiál. | Az egyenletben bevezettük a $k$ hullámszámot, amelyet a $k=\frac{\omega}{c}$ összefüggés definiál. | ||
| 67. sor: | 68. sor: | ||
{{eq|\varphi_n(x){{=}}A_n\sin\left(\frac{n\pi}{L}x\right).\quad (n{{=}}1,\,2,\,3,\dots)|eq:10|(10)}} | {{eq|\varphi_n(x){{=}}A_n\sin\left(\frac{n\pi}{L}x\right).\quad (n{{=}}1,\,2,\,3,\dots)|eq:10|(10)}} | ||
| − | Az $A_n$ állandót | + | Az $A_n$ állandót – vagyis az amplitúdó maximális értékét – a gerjesztés körülményei (a kezdeti feltételek) határozzák meg, ez azonban vizsgálataink szempontjából érdektelen. Feltételezve, hogy a húrban egyetlen $n$ értéknek megfelelő állóhullám-alakzat jött létre, az [[#eq:1|(1)]] egyenlet megoldása végül az alábbi módon irható fel: |
{{eq|\varphi_n(x,t){{=}}A_n\sin\left(\frac{2\pi}{\lambda_n}x\right)\sin(\omega_n t+\alpha_n).\quad (n{{=}}1,\,2,\,3,\dots)|eq:11|(11)}} | {{eq|\varphi_n(x,t){{=}}A_n\sin\left(\frac{2\pi}{\lambda_n}x\right)\sin(\omega_n t+\alpha_n).\quad (n{{=}}1,\,2,\,3,\dots)|eq:11|(11)}} | ||
{{fig|Állóhullámok_megfeszített,_rugalmas_húrban_1.png|fig:1|1. ábra}} | {{fig|Állóhullámok_megfeszített,_rugalmas_húrban_1.png|fig:1|1. ábra}} | ||
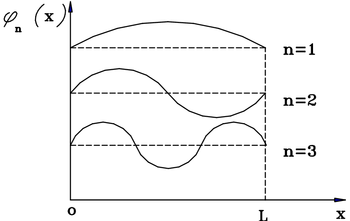
| − | A létrejött állóhullám lehetséges amplitúdó-eloszlásait a [[#eq:10|(10)]] megoldás adja meg. A megfelelő | + | A létrejött állóhullám lehetséges amplitúdó-eloszlásait a [[#eq:10|(10)]] megoldás adja meg. A megfelelő – csomópontokat és duzzadóhelyeket tartalmazó – amplitúdó-eloszlások az [[#fig:1|1. ábrán]] láthatók néhány $n$ érték esetén. A [[#eq:10|(10)]] egyenletből az is látszik, hogy adott $n$ esetén a csomópontok egymástól mért $d_n$ távolsága |
$$d_n=\frac{L}{n}=\frac{\lambda_n}{2}.$$ | $$d_n=\frac{L}{n}=\frac{\lambda_n}{2}.$$ | ||
| 100. sor: | 101. sor: | ||
A különböző állóhullám alakzatok (rezonanciák) keresésekor a gerjesztő frekvenciát kb. 50 Hz-től kezdve lassan növeljük, közben figyeljük a detektor jelét és a húr hangját: stabil állóhullám alakzat (rezonancia) elérésekor a jelnek és a hang erősségének maximuma van. Ha a jel kicsi, először próbáljuk a detektor tekercset elmozdítani, ha ez sem segít, akkor növeljük a gerjesztő jel amplitúdóját. A maximum észlelése után a detektort húzzuk végig a húr mentén, és a jel-amplitúdó helyfüggéséből állapítsuk meg az állóhullám jellegét és a hozzátartozó $n$ értékét. | A különböző állóhullám alakzatok (rezonanciák) keresésekor a gerjesztő frekvenciát kb. 50 Hz-től kezdve lassan növeljük, közben figyeljük a detektor jelét és a húr hangját: stabil állóhullám alakzat (rezonancia) elérésekor a jelnek és a hang erősségének maximuma van. Ha a jel kicsi, először próbáljuk a detektor tekercset elmozdítani, ha ez sem segít, akkor növeljük a gerjesztő jel amplitúdóját. A maximum észlelése után a detektort húzzuk végig a húr mentén, és a jel-amplitúdó helyfüggéséből állapítsuk meg az állóhullám jellegét és a hozzátartozó $n$ értékét. | ||
| − | Az állóhullám frekvenciáját mindig a detektor jelének vizsgálatával határozzuk meg: vagy a jel periódus-idejének közvetlen mérésével az oszcilloszkópon, vagy | + | Az állóhullám frekvenciáját mindig a detektor jelének vizsgálatával határozzuk meg: vagy a jel periódus-idejének közvetlen mérésével az oszcilloszkópon, vagy – ha kétsugaras oszcilloszkópot használunk – a gerjesztő jellel való összehasonlítás útján. |
===Mérési felszerelés=== | ===Mérési felszerelés=== | ||
A lap 2012. szeptember 4., 16:26-kori változata
A mérés célja:
- az állóhullámokkal kapcsolatos ismeretek elmélyítése,
- az állóhullámokra és a hullámterjedésre vonatkozó legfontosabb összefüggések kísérleti ellenőrzése.
A cél érdekében:
- összefoglaljuk az állóhullámokra vonatkozó alapvető ismereteket,
- megvizsgáljuk egy mindkét végén rögzített húrban ki-alakuló állóhullámokat,
- hullámhossz- és frekvenciamérésekkel meghatározzuk a húrban a hang terjedési sebességét, és annak függését a húr jellemző adataitól.
Tartalomjegyzék |
Elméleti összefoglaló
Kísérleteink során mindkét végén rögzített húrban terjedő hullámokat vizsgálunk. A hullám leírásánál feltételezzük, hogy a hullámterjedés egydimenziósnak tekinthető (a hullám a húr mentén terjed), a hullám transzverzális (a húr pontjainak elmozdulásvektorai a húrra merőlegesek) és síkban polarizált (a pontok elmozdulásvektorai mindig ugyanabban a síkban vannak). Ez azt jelenti, hogy a húr pontjainak az egyensúlyi helyzetből való kitérése (elmozdulása) egyetlen skaláris mennyiséggel jellemezhető. A hullám leírására a fentiek alapján a húrral párhuzamosan választott 
-tengely esetén a
![\[c^2\frac{\partial^2\psi(x,t)}{\partial x^2}=\frac{\partial^2\psi(x,t)}{\partial t^2}\]](/images/math/b/0/e/b0ef9cf2519684045e4864c4f433945e.png)
egydimenziós hullámegyenletet használhatjuk. Itt koordináta, 
az idő, a kitérés hely- és időfüggését megadó – tehát a hullám terjedését leíró – hullámfüggvény, 
pedig a hullám terjedési sebessége a húron. Ha a hullámegyenletet a húr esetére levezetjük, akkor kiderül, hogy a terjedési sebessége a húrt megfeszítő erőtől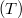 
és a húr egységnyi hosszára jutó tömegtől 
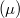függ, és ezekkel az alábbi módon fejezhető ki
![\[c=\sqrt{\frac{T}{\mu} }.\]](/images/math/2/3/c/23c5f62f18ab564971630dfe28296353.png)
A húrban valamilyen külső gerjesztés hatására kialakuló hullám általában igen bonyolult. Tapasztalatból tudjuk azonban, hogy meghatározott frekvenciákon történő gerjesztés esetén a húron, a végekről visszaverődő hullámok interferenciája révén sajátos, állandósult hullámalakzat – ún. állóhullám – jön létre. Ennek jellegzetessége az, hogy a húr meghatározott szakaszán levő pontok azonos fázisban rezegnek, a rezgés amplitúdója pedig a hely függvénye. Ez matematikailag úgy fogalmazható meg, hogy az (1) egyenletnek létezik olyan megoldása, amely egy csak helytől és egy csak időtől függő függvény szorzata [az (1) parciális differenciálegyenletben a változók szeparálhatók]. Harmonikus gerjesztés esetén ez a megoldás a
![\[\psi(x,t)=\varphi(x)\sin(\omega t+\alpha)\]](/images/math/2/2/2/222ded6048c1a13c8cede3f8388971de.png)
alakban írható fel, ahol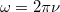 
a rezgés körfrekvenciája (
frekvencia, Hz), 
pedig a fázisszög.
A (3) megoldást az (1) egyenletbe helyettesítve az időfüggő rész kiesik, a helyfüggő részre pedig – amely a rezgés amplitúdójának a húr mentén való változását adja meg – az alábbi közönséges másodrendű differenciál-egyenletet eredményezi:
![\[\frac{\mathrm{d}^2\varphi(x)}{\mathrm{d}x^2}+k^2\varphi(x)=0.\]](/images/math/1/a/4/1a4dbdd689c337c08082a35e523a162e.png)
Az egyenletben bevezettük a 
hullámszámot, amelyet a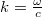 
összefüggés definiál.
A (4) egyenlet általános megoldása
![\[\varphi(x)=A\sin(kx)+B\cos(kx),\]](/images/math/3/8/3/383ae33439eaff0692626840ac8120c1.png)
ahol 
és 
tetszőleges állandók, melyeket a konkrét fizikai feltételek határoznak meg. Esetünkben az egyik ilyen feltétel az, hogy a húr két vége rögzített, ami azt jelenti, hogy itt a kitérés mindig nulla. Emiatt a matematikailag lehetséges (5) általános megoldásnak csak olyan alakjai lehetnek elfogadhatóak, amelyekre fennáll, hogy
![\[\varphi(0)=0,\]](/images/math/5/d/a/5da23fd530f533cccb3fc2a495840cce.png)
![\[\varphi(L)=0,\]](/images/math/7/b/6/7b6e22ae6f19f52c7dd9141c6393f7f1.png)
(koordinátarendszerünk kezdőpontja a húr egyik vége, így a másik végpont koordinátája 
, a húr hossza).
Könnyen belátható, hogy a (6a) határfeltétel csak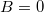 
esetén elégíthető ki, vagyis a megoldás csak egy
![\[\varphi(x)=A\sin(kx)\]](/images/math/5/a/f/5af45621e42ad9438608213c3979da03.png)
típusú függvény lehet, de a (6b) feltétel miatt ez is csak akkor, ha a k hullámszám értéke a
![\[k_n=n\frac{\pi}{L},\quad (n=1,\,2,\,3,\dots)\]](/images/math/f/b/9/fb9bb0d5c43f34a9b60b5589eed93a98.png)
összefüggéssel meghatározott értékeket veszi fel.
Mivel a hullámszám a 
hullámhosszal egyértelmű kapcsolatban van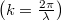 
, a (7) feltétel azt jelenti, hogy állóhullám csak meghatározott
![\[\lambda_n=\frac{2L}{n},\quad (n=1,\,2,\,3,\dots)\]](/images/math/d/0/b/d0b356e91b8ecc2ab92c3c6673e537bd.png)
hullámhosszak esetén jön létre. Ez a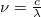 
összefüggés miatt egyben azt is jelenti, hogy meghatározott terjedési sebességgel [ami húrnál a (2) egyenlet miatt meghatározott feszítőerőt és lineáris sűrűséget jelent] a húr rezgési frekvenciája sem lehet tetszőleges, hanem csak a
![\[\nu_n=n\frac{c}{2L},\quad (n=1,\,2,\,3,\dots)\]](/images/math/d/3/d/d3d776cba4732e92fde913eb6958fe3d.png)
értékeket veheti fel. Ezek a frekvenciák a húr rezonancia-frekvenciái.
A fentiek alapján a határfeltételeket kielégítő megoldások az alábbi alakban írhatók fel:
![\[\varphi_n(x)=A_n\sin\left(\frac{n\pi}{L}x\right).\quad (n=1,\,2,\,3,\dots)\]](/images/math/1/6/5/165b524451e15ef75d0fb6fa3ac620f2.png)
Az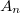 
állandót – vagyis az amplitúdó maximális értékét – a gerjesztés körülményei (a kezdeti feltételek) határozzák meg, ez azonban vizsgálataink szempontjából érdektelen. Feltételezve, hogy a húrban egyetlen 
értéknek megfelelő állóhullám-alakzat jött létre, az (1) egyenlet megoldása végül az alábbi módon irható fel:
![\[\varphi_n(x,t)=A_n\sin\left(\frac{2\pi}{\lambda_n}x\right)\sin(\omega_n t+\alpha_n).\quad (n=1,\,2,\,3,\dots)\]](/images/math/5/b/0/5b0f028079986f51bff69d6a9eb6ae4d.png)
A létrejött állóhullám lehetséges amplitúdó-eloszlásait a (10) megoldás adja meg. A megfelelő – csomópontokat és duzzadóhelyeket tartalmazó – amplitúdó-eloszlások az 1. ábrán láthatók néhány érték esetén. A (10) egyenletből az is látszik, hogy adott esetén a csomópontok egymástól mért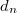 
távolsága
![\[d_n=\frac{L}{n}=\frac{\lambda_n}{2}.\]](/images/math/a/8/c/a8c4af901c9e937442e024acbe505054.png)
A különböző értékekhez – a (9) összefüggésnek megfelelően – különböző frekvenciák ill. hangmagasságok tartoznak. A szokásos elnevezés szerint az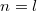 
értékhez tartozó hang a húr alaphangja, míg a magasabb értékekhez tartozók a felharmonikusok.
Itt jegyezzük meg, hogy egy húr szokásos gerjesztésekor (pl.: pengetéssel, vonóval) általában sok lehetséges rezgési forma jelenik meg egyidejűleg. [Matematikailag ez azt jelenti, hogy a hullámegyenlet megoldása az egyes rezgési formákhoz tartozó (11) típusú megoldások összege.] Egy húrnak azért lehet mégis meghatározott hangmagassága, mert az alaphang amplitúdója rendszerint sokkal nagyobb, mint a felharmonikusoké. Mindig megszólalnak azonban a felharmonikusok is: ezek határozzák meg a húr hangjának hangszínét.
Méréseink során harmonikus (szinuszos) gerjesztést alkalmazunk, ezért a húrban a frekvencia megfelelő megválasztásával különböző értékekhez tartozó állóhullám-formákat tudunk létrehozni. Mivel azonban a gerjesztés meglehetősen bonyolult folyamat, a létrejött hullámalakzat meghatározásánál legyünk óvatosak és azt ne a gerjesztő rezgés frekvenciája alapján, hanem közvetlen mérés útján próbáljuk azonosítani. A gerjesztés során ugyanis – minden igyekezetünk ellenére – a húrban több rezgési forma gerjesztődik és előfordulhat, hogy ezek közül nem a gerjesztő rezgés frekvenciájának, hanem valamelyik felharmonikusának megfelelő forma válik dominánssá. Így a gerjesztett rezgés frekvenciája a gerjesztő frekvencia egészszámú többszöröse is lehet.
A mérőberendezés és használata
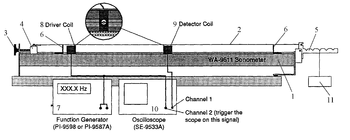
A mérőberendezés (2. ábra) egy alaplapra (1) szerelt, megfeszített acél húr (2), melynek végei egy csavarral (3) mozgatható alumínium tömbhöz (4), ill. a kétkarú emelőhöz (5) csatlakoznak. A húrhosszúság csúsztatható támaszokkal (6) szabályozható. A rezgést egy függvénygenerátorral (7) meghajtott gerjesztő tekercs (8) hozza létre mágneses csatolás révén, melynek hatására transzverzális- és gyakorlatilag síkban polarizált hullámok keletkeznek a húron. A létrejövő rezgést egy detektor-tekerccsel (9) észleljük, melynek jelét (a gerjesztő jellel együtt) kétsugaras oszcilloszkópon (10) jelenítjük meg. A húrt feszítő erőt az (5) emelő megfelelő karjára (a hosszabb, a használat során a vízszintes kar) akasztott súllyal (11) hozzuk létre.
A húr rögzítése: Az (5) emelő karján levő résbe a húr egyik végét úgy helyezzük be, hogy a rajta levő sárgaréz bütyök megakadjon, a másik végén levő fület pedig a (4) tömbön levő csavarra akasztjuk. Ehhez a tömböt a (3) csavarral a szükséges mértékben elmozdítjuk. Ezután ugyanezen csavarral a húrt megfeszítjük, úgy hogy az emelő erőkarja vízszintes legyen.
A berendezéssel a mérés szempontjából fontos paraméterek az alábbi módon változtathatók:
- A húr vizsgált hosszát a (6) támaszok eltolásával változtathatjuk.
- A húrt feszítő erő az erőkarra akasztott tömeg helyének (az erőkar hosszának) változtatásával szabályozható. Az emelő kialakítása olyan, hogy a feszítő erő megegyezik a felakasztott tömeg súlyával, ha az a tengelytől számított első vájatban van, az erő kétszeres, ha második vájatban van, stb. (A súly felhelyezése után a (3) csavarral mindig állítsuk be az erőkar vízszintes helyzetét).
- A húr egységnyi hosszra eső tömegét a húr kicserélésével tudjuk változtatni. Az egyes húrok
értéke az átmérő méréséből (csavarmikrométer) az acél ismert (7800 kgm−3) sűrűségének felhasználásával számolható ki.
- A húron létrejövő állóhullám alakzatot a függvénygenerátor frekvenciájának változtatásával módosíthatjuk.
A mérés során a függvénygenerátort szinuszos rezgésre állítsuk, a gerjesztő tekercset pedig az egyik támaszhoz közel (kb. 5 cm) helyezzük el (leghatékonyabban csomópont közelében működik). A detektor tekercset kezdetben a vizsgált húrszakasz közepe tájához tegyük, majd a feladatnak megfelelően változtassuk meg helyét. (A detektor a legnagyobb jelet a duzzadóhely közelében adja.)
A különböző állóhullám alakzatok (rezonanciák) keresésekor a gerjesztő frekvenciát kb. 50 Hz-től kezdve lassan növeljük, közben figyeljük a detektor jelét és a húr hangját: stabil állóhullám alakzat (rezonancia) elérésekor a jelnek és a hang erősségének maximuma van. Ha a jel kicsi, először próbáljuk a detektor tekercset elmozdítani, ha ez sem segít, akkor növeljük a gerjesztő jel amplitúdóját. A maximum észlelése után a detektort húzzuk végig a húr mentén, és a jel-amplitúdó helyfüggéséből állapítsuk meg az állóhullám jellegét és a hozzátartozó értékét.
Az állóhullám frekvenciáját mindig a detektor jelének vizsgálatával határozzuk meg: vagy a jel periódus-idejének közvetlen mérésével az oszcilloszkópon, vagy – ha kétsugaras oszcilloszkópot használunk – a gerjesztő jellel való összehasonlítás útján.
Mérési felszerelés
PASCO állóhullám berendezés (húr befogó + feszítő, gerjesztő, érzékelő), hanggenerátor, kétsugaras oszcilloszkóp, multiméter, kábelek, terhelő súly.
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
1. Állítsa be a 60 cm-es húrhosszúságot, majd feszítse meg a húrt kb. 60 N erővel (pl. 2 kg tömeget az emelő erőkarjának harmadik vájatába akasztva)! A gerjesztő frekvencia változtatásával állítsa elő az első öt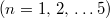 
állóhullám alakzatot! Mindegyiknél mérje meg a frekvenciát, az egyes csomópontok és duzzadóhelyek koordinátáit (pl. a húr egyik végétől mérve) és a mért koordináták alapján állapítsa meg az állóhullám hullámhosszát! Az eredményeket foglalja táblázatba! Ellenőrizze, hogy teljesül-e a (8) összefüggés!
2. Ábrázolja az egyes állóhullám-alakzatok frekvenciáját (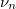
) az alakzat sorszámának függvényében, és illesszen egyenest a pontokra! Mérje meg a húr hosszát, majd az egyenes meredekségéből számítsa ki a hang c terjedési sebességét a húrban! Vesse össze az értéket a (2) összefüggésből számolt hangsebességgel!
3. Állítsa elő az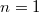 
-hez tartozó állóhullámot változatlan feszítő erő, de négy másik hosszúság esetén is, és mindegyik esetben mérje meg a rezgés frekvenciáját! Ábrázolja a frekvenciát a húr hosszúság reciprokának függvényében, majd illesszen a mérési pontokra egyenest! Határozza meg ismét a hang terjedési sebességét, vesse össze a korábban kapott értékekkel!
4. Kiválasztva az egyik húrt, állítson be kb. 60 cm-es húrhosszúságot, akasszon egy súlyt az emelő erőkarjának első vájatába, majd a gerjesztő frekvencia változtatásával állítsa be az első állóhullám alakzatot (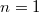)! Mérje meg az állóhullám hullámhosszát és frekvenciáját és a 
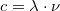összefüggés alapján számítsa ki a hang terjedési sebességét a húrban! Készítsen táblázatot és írja be a 
feszítő erő, a lineáris sűrűség, a alapfrekvencia és a terjedési sebesség értékeit! Ismételje meg a mérést még négy különböző feszítő erővel (a súlyt helyezze egyre távolabb az emelő tengelyétől) és írja be ismét az adatokat a táblázatba! Ezután közepes feszítő erőnél ismételje meg a mérést a mérőhelyen található többi húrral, és ismét írja be az adatokat a táblázatba!
5. Az 4. pontban kapott táblázat alapján ellenőrizze a (2) egyenletet! (Az egyenlet szerint állandó mellett a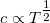 
összefüggés lineáris, állandó mellett pedig a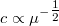 
összefüggés lineáris.) Ha a táblázat alapján elkészítjük ezeket a grafikonokat, akkor a pontoknak egy egyenesen kell lenniük és a meredekség az első esetben 
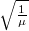, második esetben pedig 
.
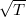