„Szilárdtestfizika gyakorlat” változatai közötti eltérés
(Új oldal, tartalma: „Kategória:Fizika BSC alapképzés <!--Kategória:Fizika BSC alkalmazott fizika szakirány--> <!--Kategória:Fizika BSC fizikus szakirány--> <!--[[Kategória:…”) |
(→Tematika) |
||
| 45. sor: | 45. sor: | ||
==Tematika== | ==Tematika== | ||
| − | * ''Kristályok szimmetriái'' Nevezetes rácsok és reciprok rácsaik. Miller index, kristály síkok, reciprok rácsvektorok kapcsolata. Neumann-elv. | + | * '''Kristályok szimmetriái.''' Nevezetes rácsok és reciprok rácsaik. Miller index, kristály síkok, reciprok rácsvektorok kapcsolata. Neumann-elv. |
| − | * | + | * '''Röntgen-diffrakció tökéletes kristályon.''' Rácsösszeg. Atomi alaktényezõ számítása különbözõ töltéseloszlások esetén. |
| − | Röntgen-diffrakció tökéletes kristályon | + | * '''Röntgen-diffrakció nem-tökéletes kristályon.''' Rácsrezgések figyelembe vétele. Véletlen ötvözetek. |
| − | Rácsösszeg. Atomi alaktényezõ számítása különbözõ töltéseloszlások esetén. | + | * '''Rácsrezgések dinamikája.''' Két dimenziós rácsok rugós modelljei. Rezgési módusok és frekvenciájuk. |
| − | Röntgen-diffrakció nem-tökéletes kristályon | + | * '''Rácsfajhõ és állapotsûrûség.''' Az állapotsûrûség viselkedése különbözõ dimenziókban izotrop és anizotrop hangsebesség esetén. Debye-modell. Debye-Waller faktor. Lindemann kritérium az olvadáspontra. |
| − | Rácsrezgések figyelembe vétele. Véletlen ötvözetek. | + | * '''Elektronok szoros kötésû közelítésben.''' Atomi hullámfüggvények egydimenziós Dirac-delta potenciál esetén. Elektronok kétdimenziós ferdeszögû rácsban. S- és p-típusú pályák. |
| − | Rácsrezgések dinamikája | + | * '''Kváziszabad elektron közelítés.''' Tilos sáv számítása egydimenziós Dirac-delta potenciál esetén. Elektronsávok négyzetrács esetén. |
| − | Két dimenziós rácsok rugós modelljei. Rezgési módusok és frekvenciájuk. | + | * '''Elektronok állapotsûrûsége és fajhõje.''' Fermi-hullámszám számítása. Állapotsûrûség kétdimenziós derékszögû tight-binding modellben kis betöltés esetén. |
| − | Rácsfajhõ és állapotsûrûség | + | |
| − | Az állapotsûrûség viselkedése különbözõ dimenziókban izotrop és anizotrop hangsebesség esetén. Debye-modell. Debye-Waller faktor. Lindemann kritérium az olvadáspontra. | + | |
| − | Elektronok szoros kötésû közelítésben | + | |
| − | Atomi hullámfüggvények egydimenziós Dirac-delta potenciál esetén. Elektronok kétdimenziós ferdeszögû rácsban. S- és p-típusú pályák. | + | |
| − | Kváziszabad elektron közelítés | + | |
| − | Tilos sáv számítása egydimenziós Dirac-delta potenciál esetén. Elektronsávok négyzetrács esetén. | + | |
| − | Elektronok állapotsûrûsége és fajhõje | + | |
| − | Fermi-hullámszám számítása. Állapotsûrûség kétdimenziós derékszögû tight-binding modellben kis betöltés esetén. | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Részletes tematika== | ==Részletes tematika== | ||
A lap 2012. szeptember 3., 06:18-kori változata
Tartalomjegyzék[elrejtés] |
Általános adatok (2012 ősz)
- Kód: BMETE11AF06;
- Követelmény: 0/2/0/F/2;
- Félév: ősz;
- Nyelv: magyar;
- Tárgyfelelős: Dr. Készmárki István egyetemi docens
- Gyakorlatvezetők: Dr. Kézsmárki István, Bácsi Ádám, Kanász-Nagy Márton
- A gyakorlatok időpontja: csütörtök 14:15-16:00
- Helyszín: T606 (K.I. csoportja), T604 (B.Á. csoportja), T601/2 (K-N.M. csoportja)
- Jelenléti követelmények: A félév végi aláírás feltétele előadások legalább 70%-án való részvétel. Az előadásokon jelenléti ívet vezetünk.
- Félévközi számonkérések: azonosak a [Szilárdtestfizika gyakorlat] számonkéréseivel.
- Félév végi osztályzat: írásbeli és szóbeli vizsga. A vizsga feltétele az aláírás, valamint a gyakorlati jegy megszerzése.
Tematika
- Kristályok szimmetriái. Nevezetes rácsok és reciprok rácsaik. Miller index, kristály síkok, reciprok rácsvektorok kapcsolata. Neumann-elv.
- Röntgen-diffrakció tökéletes kristályon. Rácsösszeg. Atomi alaktényezõ számítása különbözõ töltéseloszlások esetén.
- Röntgen-diffrakció nem-tökéletes kristályon. Rácsrezgések figyelembe vétele. Véletlen ötvözetek.
- Rácsrezgések dinamikája. Két dimenziós rácsok rugós modelljei. Rezgési módusok és frekvenciájuk.
- Rácsfajhõ és állapotsûrûség. Az állapotsûrûség viselkedése különbözõ dimenziókban izotrop és anizotrop hangsebesség esetén. Debye-modell. Debye-Waller faktor. Lindemann kritérium az olvadáspontra.
- Elektronok szoros kötésû közelítésben. Atomi hullámfüggvények egydimenziós Dirac-delta potenciál esetén. Elektronok kétdimenziós ferdeszögû rácsban. S- és p-típusú pályák.
- Kváziszabad elektron közelítés. Tilos sáv számítása egydimenziós Dirac-delta potenciál esetén. Elektronsávok négyzetrács esetén.
- Elektronok állapotsûrûsége és fajhõje. Fermi-hullámszám számítása. Állapotsûrûség kétdimenziós derékszögû tight-binding modellben kis betöltés esetén.
Részletes tematika
Kristálytan - Szerkezetvizsgálat
Kristály = Rács + Bázis
Kristályrendszerek (eltolás + egy definiáló szimmetria) Bravais-rácsok (élhossz és szögek szerinti osztályozás) Pontcsoportok, Tércsoportok
Elemi cella, Wigner-Seitz cella Kristály síkok, Miller-index Reciprok rács, Brillouin-zóna
Diffrakció elmélete: Bragg-feltétel, Laue féle leírás, Szerkezeti tényező, atomi alaktényző
Rugalmas szóráskisérletek: Ewald szerkesztés, Debye-Scherrer- és Laue-módszer Röntgen-, elektron- és neutron-szórási mechanizmus Szinkrotron-sugárzás
Kvázikristályok Nem-kristályos szilárd testek (páreloszlási függvény) Ponthibák, vonalhibák (diszlokációk)
Rácsrezgések - fononok
Szilárd testek fajhőjének Einstein- és Debye-modellje
Lineáris lánc rezgései Rácsrezgések 3 dimenzióban (Dinamikus mátrix sajátérték-egyenlete) Rugalmas hullámok
Diszperziós reláció Állapotsűrűség, Van Hove szingularitás
Kvantummechanikai leírás Fonon-energia és impulzus, a fonongáz fajhője
A diszperziós reláció kisérleti meghatározása: Megmaradási tételek részecske-fonon, ill. foton-fonon kölcsönhatáskor
Rugalmatlan neutron-szórás
Elektronok
Szabad elektrongáz kvantummechanikai leírása: A Fermi-statisztika, Sommerfeld-sorfejtés Fajhő, szuszceptibilitás
Elektronok periodikus potenciálban: Bloch-tétel, Energiaspektrum perturbációs számolása Szoros kötésű közelítés Sávszerkezet, diszperziós reláció
Elektronok propagálása mágneses térben:
Kváziklasszikus közelítés
Ciklotron frekvencia
Drude-modell: vezetőképesség, Hall-állandó diszperziós reláció, optikai tulajdonságok
Tételek
- Kristályrács definíciója. Reciprok-rács, kristálysíkok, Miller-index. Szimmetriaműveletek, kristályrendszerek, Bravais-rácsok.
- Diffrakció elmélete. Szerkezeti tényező, atomi szórási tényező. Röntgen-, elektron- és neutron-szórási kísérletek. Kvázikristályos és amorf anyagok.
- Rácsrezgések diszperziós relációja. A dinamikus mátrix sajátérték-egyenlete. Akusztikus és optikai ágak. A diszperziós reláció kísérleti meghatározása.
- Szilárd testek fajhőjének kvantummechanikai leírása. Bose-Einstein eloszlás. Az állapotsűrűség számolása. Debye-modell.
- Szabad elektrongáz kvantummechanikai leírása. Elektron-fajhő, fémek mágneses szuszceptibilitása (Sommerfeld-sorfejtés).
- Bloch-tétel. Közel szabad elektron modell. Sávszerkezet.
 (k) kísérleti meghatározása: szögfelbontású fotoelektron-spektroszkópia (ARPES).
(k) kísérleti meghatározása: szögfelbontású fotoelektron-spektroszkópia (ARPES).
- Wannier-függvények. Szoros kötésű közelítés. Lokalizált és kiterjedt elektronállapotok. Effektív tömeg.
- Hullámcsomag. Elektronok mágneses térben:ciklotron frekvencia. Landau-nívók. Drude-modell: Hall-állandó,
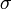 (
(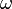 ),
),  (
(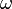 ).
).
Irodalom
Charles Kittel: Introduction to Solid State Physics, 6th edition, John Wiley & Sons, New York (1986). Neil W. Aschcroft and N.David Mermin: Solid State Physics, Sauders Collage, Philadelphia (1976). Sólyom Jenő: A modern szilárdtestfizika alapjai I, A szilárd testek szerkezete és dinamikája, ELTE Eötvös Kiadó, Budapest (2002).