„Fénytörés és visszaverődés vizsgálata” változatai közötti eltérés
| 47. sor: | 47. sor: | ||
avagy kifejezve az áthaladó fény intenzitását a közeg törésmutatójával: | avagy kifejezve az áthaladó fény intenzitását a közeg törésmutatójával: | ||
| − | $$ I_0 = I_R + I_0\frac{4n}{(n+1)^2} $$ | + | $$ I_0 = I_R + I_0\frac{4n}{(n+1)^2} $$. |
| + | A visszaverődő fény intenzitását kifejezve az | ||
| + | $$ I_R = \left( \frac{n-1}{n+1}\right) ^2 I_0 $$ | ||
| + | összefüggés adódik. Jól látható, hogy még merőleges beesésnél is a sugárzás egy jelentős hányada visszaverődik (pl. $n = 1,5$ törésmutatójú üveget véve alapul, a beeső fény intenzitásának 4 %-a verődik vissza). Ha a veszteségektől eltekintünk, az áthaladó intenzitás a leírt összefüggések alapján meghatározható. | ||
| + | |||
| + | Most vizsgáljuk meg azon eseteket, amikor lineárisan poláros fény esik a felületre ''(a)'' úgy, hogy a fény rezgési síkja merőleges a beesési síkra, ill. ''(b)'' a rezgési sík párhuzamos a beesési síkkal. Emlékeztetőül: a beesési sík a beeső, a visszavert és a megtört sugarak által meghatározott sík. A fenti két esetnek megfelelő viszonyokat az ''1. ábrán'' vázoltuk, ahol körrel jelöltük a síkra merőleges, és sugárra merőleges kétirányú nyíllal a párhuzamos rezgést. | ||
| + | A számolások részletezése nélkül (ez bármelyik optikával foglalkozó kézikönyvben megtalálható) megadjuk az ún. Fresnel-formulákat, melyek a fenti eseteknek megfelelő amplitúdó ($\Psi$) viszonyokat írják le. Az (a) esetre | ||
</wlatex> | </wlatex> | ||
A lap 2012. szeptember 29., 16:01-kori változata
Szerkesztés alatt!
A mérés célja:
- elmélyíteni a hallgatók geometriai optikai ismereteit.
Ennek érdekében:
- áttekintjük a fénytörés és visszaverődés elméletét,
- geometriai optikai méréseket végzünk,
- vizsgáljuk a polarizált fény visszaverődését.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Törésmutató meghatározása a reflexió vizsgálatával
A testeket érő elektromágneses sugárzás részben visszaverődik a felületről, részben elnyelődik, egy része pedig áthalad rajta. Ezen három rész intenzitás-aránya anyagonként más és más, és függ a hullámhossztól is.
Méréstechnikai szempontból legegyszerűbben a visszaverődő és az áthaladó hányad mérhető meg, míg az elnyelt részt az energia-megmaradás törvénye alapján határozhatjuk meg. Minthogy az elektromágneses sugárzás transzverzális, így nem lényegtelen megvizsgálnunk, hogy milyenek a polarizációs viszonyok a visszaverődéskor. Ezért tanulmányozzuk a lineárisan poláros fény visszaverődését is.
Essen két közeg határfelületére lineárisan poláros,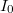 
intenzitású fény. Legyen az első közeg levegő, míg a másodiknak a levegőre vonatkozó törésmutatója 
. A beeső, a visszaverődő és a megtört sugárzás intenzitásait jelölje , 
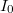, és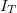 
. Az egyszerűség kedvéért itt eltekintünk az elnyelődéstől.
Tudjuk, hogy merőleges beesésnél a visszavert és a megtört sugár egyaránt merőlegesek a felületre és az intenzitásokra az energia-megmaradás értelmében:
![\[ I_0 = I_R + I_T \]](/images/math/6/6/e/66e5071e95175dfa38414adba00e98bc.png)
avagy kifejezve az áthaladó fény intenzitását a közeg törésmutatójával:
![\[ I_0 = I_R + I_0\frac{4n}{(n+1)^2} \]](/images/math/3/4/6/346ef3a1d526c01a8eed48a9f8dc036d.png)
A visszaverődő fény intenzitását kifejezve az
![\[ I_R = \left( \frac{n-1}{n+1}\right) ^2 I_0 \]](/images/math/f/6/3/f63cdec0a810209eb6d17bf3fb043f8c.png)
összefüggés adódik. Jól látható, hogy még merőleges beesésnél is a sugárzás egy jelentős hányada visszaverődik (pl.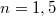 
törésmutatójú üveget véve alapul, a beeső fény intenzitásának 4 %-a verődik vissza). Ha a veszteségektől eltekintünk, az áthaladó intenzitás a leírt összefüggések alapján meghatározható.
Most vizsgáljuk meg azon eseteket, amikor lineárisan poláros fény esik a felületre (a) úgy, hogy a fény rezgési síkja merőleges a beesési síkra, ill. (b) a rezgési sík párhuzamos a beesési síkkal. Emlékeztetőül: a beesési sík a beeső, a visszavert és a megtört sugarak által meghatározott sík. A fenti két esetnek megfelelő viszonyokat az 1. ábrán vázoltuk, ahol körrel jelöltük a síkra merőleges, és sugárra merőleges kétirányú nyíllal a párhuzamos rezgést.
A számolások részletezése nélkül (ez bármelyik optikával foglalkozó kézikönyvben megtalálható) megadjuk az ún. Fresnel-formulákat, melyek a fenti eseteknek megfelelő amplitúdó (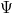
) viszonyokat írják le. Az (a) esetre
