„Mérések Michelson-interferométerrel” változatai közötti eltérés
| 82. sor: | 82. sor: | ||
$$|\pmb{k}| = k = \frac{2\pi}{\lambda},$$ | $$|\pmb{k}| = k = \frac{2\pi}{\lambda},$$ | ||
| − | $$\pmb{kx} = kx sin \ | + | $$\pmb{kx} = kx sin \theta \approx kx\theta \; (\theta\ll1), $$ |
| − | $$ f(x) = \begin{cases} \frac{1}{d} \; ha \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] | + | $$ f(x) = \begin{cases} \frac{1}{d} \; \mathsf{ha} \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] \\ 0\; x \notin \left[-\frac{d}{2};\frac{d}{2}\right]. \end{cases} $$ |
Felhasználva, hogy | Felhasználva, hogy | ||
A lap 2012. október 2., 23:28-kori változata
Szerkesztés alatt!
A mérés célja:
- koherens optikai jelenségek tanulmányozása.
Ennek érdekében:
- áttekintjük a diffrakció és az interferencia elméletét,
- megmérjük a lézerfény koherenciahosszát,
- méréseket végzünk interferométerrel,
- diffrakciós méréseket végzünk.
Elméleti összefoglaló
Koherencia fogalma
A koherencia fogalmát a következő egyszerű képen keresztül definiálhatjuk. Tételezzük fel, hogy egy hullám egy 
kiindulási pontból két úton keresztül juthat el a 
pontba. Az 1. és 2. úton a pontba érkező nyalábokat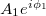 
és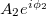 
komplex számokkal jellemezhetjük, ahol 
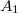és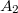 
a nyalábok amplitúdóit, 
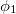és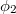 
pedig a fázisukat adják meg. B pontban a két nyaláb a szuperpozíció elve alapján összeadódik, így az eredő komplex amplitúdó 
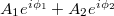lesz. Detektoraink viszont nem a komplex amplitúdót, hanem annak az abszolút érték négyzetét, az intenzitást érzékelik, mely egyszerű számolás alapján:
![\[ I_B = A_1^2 + A_2^2 + 2A_1A_2cos(\phi_1- \phi_2). \]](/images/math/4/c/9/4c9a1fe9653ae63739f224930b253b1b.png)
Látszik, hogy a két nyaláb intenzitásának összege mellett megjelenik az úgynevezett interferencia tag is: ha a két nyaláb azonos fázisban érkezik a pontba, akkor erősítést, ha ellentétes fázisban érkeznek, akkor kioltást kapunk. Persze interferenciát csak akkor tapasztalunk, ha a két nyaláb fáziskülönbsége időben állandó, ekkor beszélünk koherens nyalábokról. Ellenkező esetben az interferenciatag időben kiátlagolódik, így nem látunk erősítéseket, ill. kioltásokat.
Fény esetében az interferencia tag eltűnésének a leggyakoribb oka, hogy maga az pontban elhelyezett fényforrás sem koherens. Ha az 1. és 2. nyaláb által megtett optikai úthossz különbözik, akkor a pontban találkozó nyalábok különböző időpontban indultak el az pontból. Koherencia időnek hívjuk azt a maximális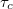 
időkülönbséget, melyre a fényforrásból a 
ill.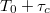 
időpontban kibocsátott fotonok fázisai között korreláció tapasztalható. Ha az 1. és 2. nyaláb optikai úthosszainak különbsége nagyobb a fény által 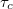idő alatt megtett útnál, 
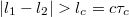, akkor az interferencia tag eltűnik. Az ennek megfelelő 
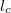úthosszat koherenciahossznak nevezzük.
Az első koherens optikai kísérletet Thomas Young végezte úgy, hogy keskeny fénynyalábot irányított két szorosan egymás mellett elrendezett résre. A résekkel szemben elhelyezett ernyőn a réseken keresztül ráeső fényből szabályos, sötét és világos sávokból álló interferenciakép jött létre. Young kísérlete fontos bizonyítéka volt a fény hullámtermészetének. 1881-ben, 78 évvel Young után, A. A. Michelson hasonló elven működő interferométert épített. Michelson kísérletében a fényhullámot egy félig áteresztő tükör segítségével választotta két részre, melyek különböző utak megtétele után (lásd később) egy detektáló ernyőn újra találkozva alkotnak interferenciaképet. Michelson eredetileg az éternek, az elektromágneses sugárzások – így a fénynek is – terjedését biztosító feltételezett közegnek a kimutatására szerkesztette meg interferométerét. Részben az ő erőfeszítéseinek is köszönhetően az éter feltételezését ma nem tekintjük életképes hipotézisnek. Ezen túlmenően azonban a Michelson-féle interferométer széleskörűen elterjedt a fény hullámhosszának mérésére illetve ismert hullámhosszúságú fényforrás alkalmazásával rendkívül kis távolságok mérésére és optikai közegek vizsgálatára.
A fenti kísérletek elvégzése hagyományos fényforrásokkal rendkívül nehéz feladat a rövid koherenciaidő, illetve a különböző frekvenciájú fénykomponensek keveredése miatt. A lézerek feltalálása óta lényegesen könnyebb interferencia-jelenségeket vizsgálni, egy vékony résen történő diffrakciót akár otthon is kipróbálhatjuk egy mutatólézer segítségével.
A lézer működési elvénél fogva egy nagy koherencia-hosszal rendelkező, jól meghatározott irányban terjedő monokromatikus fénynyalábot biztosít. A lézerben egy aktív közeg jól meghatározott frekvenciájú fotonokat emittál, melyek egy rezonátorban „oda-vissza pattognak”. A stimulált emisszió jelenségének köszönhetően az emittált fotonok a rezonátorban már jelenlévő fotonokkal azonos állapotúak lesznek, azaz a már jelenlévő fotonokkal azonos fázisú és terjedési irányú fotonok emittálódnak. A rezonátor egyik oldalán a fény egy részét kicsatolva egy irányított, koherens nyalábot kapunk. A mérésen is használt He-Ne lézerben a fényemissziót a gázkeverék bizonyos atomi átmenetei biztosítják, míg a rezonátort két szembeállított tükör alkotja, melyek egyike a fény kb. 1 %-át kiengedi. Mivel a rezonátor szélessége 10-20 cm is lehet, illetve a fotonok a kilépés előtt sokszor körbejárják a rezonátort, így a He-Ne lézer koherenciahossza az 1 métert is meghaladhatja.
A napjainkban tömegesen alkalmazott félvezető lézerekben a fény elektronok és lyukak rekombinációjának köszönhetően emittálódik. A rezonátort maga a félvezető nanoszerkezet biztosítja, így lényegesen kisebb koherenciahosszat várunk.
Michelson-féle interferométer felépítése
Az 1. ábrán a Michelson-féle interferométer vázlata látható. A lézer sugárnyalábja sugárosztóra esik, amely a beeső fény 50 %-át visszaveri, és másik 50 %-át átengedi. A beeső fény így két nyalábra oszlik. Az egyik a mozgatható tükörre (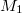
) esik, a másik a rögzített tükörre (
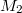) verődik. Mindkét tükör a sugárosztóra veri vissza a fényt.
A mozgatható tükörről visszavert fény egyik fele most a megfigyelő ernyőre esik be, és a rögzített tükörről visszaverődő fény fele a sugárosztón áthaladva szintén a megfigyelő ernyőre esik.
Ily módon az eredeti sugárnyaláb először kettéosztódik, majd a keletkezett nyalábok egy része visszafelé egyesül egymással. Mivel a nyalábok ugyanabból a fényforrásból származnak, fázisuk erősen korrelált. Így, amikor lencsét helyezünk a lézer fényforrás és a sugárosztó közé, a fénynyaláb kitágul és a megfigyelő ernyőn sötét és világos gyűrűkből álló kép jelenik meg (2. ábra).
Mivel a két interferáló nyaláb ugyanabból a forrásból származik, fázisuk eredetileg azonos volt. Relatív fázisuk, amikor a megfigyelő ernyő bármely pontjában találkoznak, attól az optikai úthossztól függ, amelyet ezen pont eléréséig megtettek.
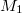mozgatásával az egyik nyaláb úthossza változtatható. Mivel a nyaláb az 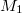és a sugárosztó közötti utat kétszer teszi meg, 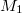-et 1/4 hullámhossznyival közelítve a sugárosztóhoz, a nyaláb úthossza 1/2 hullámhossznyival csökken. Eközben megváltozik az interferenciakép. A maximumok sugara oly módon csökken, hogy a korábbi minimumok helyét foglalják el. Ha 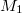-et tovább mozgatjuk 1/4 hullámhossznyival a sugárosztó felé, a maximumok sugara tovább csökken úgy, hogy a maximumok és a minimumok ismét helyet cserélnek, és az új elrendezés megkülönböztethetetlen lesz az eredeti képtől.
Lassan mozgatva a tükröt egy meghatározott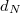 
távolságon, és közben leszámolva 
-et, annak számát, hányszor jutott a gyűrűkép az eredeti állapotába, meghatározható a fény hullámhossza:
![\[ \lambda = \frac{2d_N}{N}. \]](/images/math/8/6/0/860b9434eda02ec0f6c527f475c22728.png)
Ha a fény hullámhossza ismert, ugyanígy mérhető a 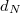távolság.
Diffrakciós kép vizsgálata
A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens-Fresnel-elv" segítségével lehet meg-magyarázni: a Huygens-Fresnel-elv alapján a hullámfelület minden pontja elemi hullámforrásnak tekintendő, és ezeknek az egymással koherens elemi gömbhullámoknak az interferenciája szabja meg a tér egy pontjában a fényhatást.
Példaképp vizsgáljuk meg az optikai rés esetét. A rés egy átlátszatlan felületen kialakított keskeny, a fény hullámhosszával összemérhető szélességű, hosszú nyílás. Világítsuk meg a rést egy koherens, párhuzamos fénynyalábbal (legegyszerűbben egy lézer fényével). A fény a résen áthaladva elhajlik. A réstől távol elhelyezett ernyőn a résből kiinduló elemi hullámok interferenciája alakítja ki a diffrakciós képet. A diffrakciós képet – az intenzitást a hely függvényében - egy fotodióda mozgatásával könnyen meg lehet mérni (3. ábra).
A k hullámszámvektor irányában a relatív intenzitást a Fourier-integrál segítségével lehet kiszámítani. Az intenzitás arányos az integrál abszolút értékének négyzetével:
![\[ I(\pmb{k}) = \left \lvert \int_{-\infty}^{\infty} e^{\pmb{kx}i}f(\pmb{x})d\pmb{x} \right \rvert^2. \]](/images/math/9/6/6/9663788744b887e93547c4b60e644842.png)
A kifejezésben
![\[|\pmb{k}| = k = \frac{2\pi}{\lambda},\]](/images/math/e/e/d/eede5e35ac948ed5edd2f2c0e0f933f8.png)
![\[\pmb{kx} = kx sin \theta \approx kx\theta \; (\theta\ll1), \]](/images/math/e/3/1/e310050aad76b2ef26d438fda246b862.png)
![\[ f(x) = \begin{cases} \frac{1}{d} \; \mathsf{ha} \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] \\ 0\; x \notin \left[-\frac{d}{2};\frac{d}{2}\right]. \end{cases} \]](/images/math/5/2/1/521f24cad97d0e017de288bcfe73c467.png)
Felhasználva, hogy
