„Optikai heterodin detektálás” változatai közötti eltérés
Lenk (vitalap | szerkesztései) |
Lenk (vitalap | szerkesztései) |
||
| 38. sor: | 38. sor: | ||
$${\bf{r}} = \int\limits_0^t {{\bf{v}}(\tau ){\rm{d}}\tau } + {\bf{r'}}$$ | $${\bf{r}} = \int\limits_0^t {{\bf{v}}(\tau ){\rm{d}}\tau } + {\bf{r'}}$$ | ||
(3) | (3) | ||
| + | Ezt beírva az (1) egyenletbe, a hullám K'-beli alakját nyerjük: | ||
| + | $$E\left( {{\bf{r'}},t} \right) = {E_0}\cos \left( {\varphi ({\bf{r'}},t)} \right) | ||
| + | = {E_0}\cos \left( {\omega t - {\bf{k}} \cdot \int\limits_0^t {{\bf{v}}(\tau | ||
| + | ){\rm{d}}\tau } - {\bf{k}} \cdot {\bf{r'}}} \right) | ||
| + | $$ | ||
==Mérési feladatok== | ==Mérési feladatok== | ||
A lap 2012. november 10., 06:39-kori változata
Tartalomjegyzék |
Szerkesztés alatt!
Elméleti összefoglaló
A hullám fogalma – a fény mint hullám
A fény, mint ismeretes, az elektromágneses tér hullámjelensége. Jellemző rezgési frekvenciája a 1014 Hz körüli tartományba esik. Az a fizikai mennyiség, amelynek terjedését egyszerűen fénynek nevezzük, az elektromos és mágneses térerősség. Tehát a fényben az elektromos és a mágneses tér változásai terjednek. Tekintsünk egy, a tárgyalás szempontjából egyszerű, lineárisan polarizált harmonikus síkhullámot. A síkhullám elnevezés onnan ered, hogy az azonos térerősségű pontok egy adott pillanatban egy síkon helyezkednek el. A síkhullám kifejezése:
![\[E\left( {{\bf{r}},t} \right) {{=}} {E_0}\cos \left( {\omega t - {\bf{kr}}} \right)\]](/images/math/6/0/b/60b98f9ce1b43f8beac900bce40ea117.png)
ahol E0 az elektromos hullám amplitúdója, k a hullámszám vektor,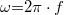 
az elektro-mágneses hullám körfrekvenciája, „f” pedig a frekvenciája. Egyszerű megfontolásokból a hullám terjedési sebessége k-val és 
-val kifejezhető:
![\[{{c = \frac{\omega }{\left| k \right|}}}\]](/images/math/5/d/4/5d492d4631dcb1bb6a6bcf00487e759c.png)
A „k” helyett a gyakorlatban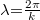 
-t szokás használni, amelyet hullámhossznak nevezünk. Így az egyenlet ismertebb alakjában 
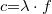. Az (1) egyenletből látszik 
szemléletes jelentése is: azt a k vektor irányában mért legkisebb távolságot jelenti, amely szerint a térerősség periodikusan változik.
Doppler-effektus
Tegyük fel, hogy az (1) szerinti monokromatikus síkhullámot egy „K” koordináta-rendszerben írtuk fel. Ha ezt a síkhullámot a K-hoz képest v(t) pillanatnyi sebességgel mozgó K' rendszerből figyeljük, akkor a hullám K-beli frekvenciájától különböző frekvenciájú hullámot fogunk észlelni. Válasszuk úgy a K és K' rendszert, hogy -ban az origók egybe essenek. Ekkor a K-beli koordinátát K'-beli koordinátákkal kifejezhetjük:
![\[{\bf{r}} = \int\limits_0^t {{\bf{v}}(\tau ){\rm{d}}\tau } + {\bf{r'}}\]](/images/math/5/1/e/51e96aacb29da120e8de44a781c4b6bd.png)
(3) Ezt beírva az (1) egyenletbe, a hullám K'-beli alakját nyerjük:
![\[E\left( {{\bf{r'}},t} \right) = {E_0}\cos \left( {\varphi ({\bf{r'}},t)} \right) = {E_0}\cos \left( {\omega t - {\bf{k}} \cdot \int\limits_0^t {{\bf{v}}(\tau ){\rm{d}}\tau } - {\bf{k}} \cdot {\bf{r'}}} \right) \]](/images/math/b/5/3/b536ce6f20faf757d9ad7d2d7c3bdb0f.png)
Mérési feladatok
