„Magnetorezisztív jelenségek vizsgálata mágneses nanoszerkezetekben” változatai közötti eltérés
| 12. sor: | 12. sor: | ||
==Anizotróp mágneses ellenállás elvén működő magnetorezisztív szenzorok== | ==Anizotróp mágneses ellenállás elvén működő magnetorezisztív szenzorok== | ||
| + | Egy mágneses anyagban a kristálytani irányok, illetve az anyag geometriája által kitüntetett irányok úgynevezett mágneses anizotrópiát okozhatnak, melynek hatására a mágneses momentumok az anizotrópia által kitüntetett, ún. könnyű mágnesezési irányba állnak be. A mérés során Phillips KMZ10A ill. KMZ10A1 típusú magnetorezisztív szenzorokat használunk. A szenzorok mágneses vékonyrétegekből készült keskeny mágneses csíkokból épülnek fel, melyekben a geometriai anizotrópia miatt zérus külső tér esetén a mágneses momentumok a csíkkal párhuzamosan szeretnek állni. Véges külső mágneses tér alkalmazásával a momentumokat elfordíthatjuk a kitüntetett irányhoz képest. A spin-pálya kölcsönhatáson alapuló bonyolult fizikai folyamatok miatt egy mágneses vékonyréteg ellenállása függ a mágneses momentumok és az áramirány által bezárt $\alpha$ szögtől, melyet anizotróp mágneses ellenállás (AMR) jelenségének nevezünk. | ||
| + | |||
| + | Egy egyszerű magnetorezisztív mintán az LINK 1. ábra szerinti elrendezésben az ellenállás az $R = R_0 + \Delta R_0 cos^2\alpha$ képlettel közelíthető. Ha a könnyű mágnesezési irányra merőleges mágneses teret alkalmazunk, a momentumok elfordulnak a mágneses anizotrópia által kitüntetett irányból, így a vékonyréteg ellenállása megváltozik. | ||
| + | |||
| + | 1. ÁBRA | ||
| + | |||
| + | Ha az áram a preferált mágnesezettség irányába folyik, az ellenállás négyzetes függvénye lesz a mágnesezettségnek, hiszen $cos \alpha $ arányos a külső térrel. Lineáris szenzorkarakterisztikát egy speciális elrendezéssel, az ún. Barber-pole segítségével érhetünk el LINK (2. ábra). Ha a mágneses vékonyrétegből egy hosszú keskeny csíkot készítünk, a mágnesezettség a hosszirányba fog beállni. A csík két vége között folyó áram irányát a vékonyréteg tetejére ferde csíkokban felpárologtatott alumíniumrétegek segítségével forgatjuk el. Az alumíniumrétegek lényegesen jobban vezetnek az alattuk levő mágneses vékonyrétegnél, ezért az elektronok "próbálják minimalizálni a vékonyrétegben töltött időt", és így a vékonyrétegben az áramirány az alumínium csíkokra merőlegesen fog beállni. | ||
| + | |||
| + | 2. ÁBRA | ||
| + | |||
| + | Az áramirányt 45°-al elforgatva a mágnesezettséghez képest lineáris szenzorkarakterisztikát kaphatunk, hiszen a $cos^2 \alpha$ függvény lineáris szakaszát használjuk. | ||
| + | A hőmérsékleti drift elkerülése érdekében a szenzor 4 db, hídkapcsolásban elhelyezett magnetorezisztív vékonyrétegből áll LINK(3. ábra). A híd két szemközti csúcsára 5V tápfeszültséget kötünk, és a másik két szemközti csúcs között mérjük a feszültséget. Zérus mágneses térben a híd kiegyenlített, így a kimeneten ideális esetben zérus feszültség látható. Véges mágneses térben a térrel arányos, tipikusan mV-os nagyságrendű jelet tapasztalunk. A szenzorokban a mágnesezettség az ábrán jelölt $H_x$ irányban áll, így $H_y$ irányú mágneses teret tudunk mérni. A KMZ10A és KMZ10A1 szenzorok közötti különbség, hogy a 10A szenzorban a preferált mágnesezési irány a forrasztólábakra merőleges irányú, míg a 10A1 szenzorban a forrasztólábakkal párhuzamos irányú. (Ennek megfelelően a 10A szenzor a lábakkal párhuzamos, míg a 10A1 szenzor a lábakra merőleges irányban méri a teret.) | ||
| + | |||
| + | |||
| + | 3. ÁBRA | ||
| + | |||
| + | A szenzor valóságos elrendezését a 4. ábrán látjuk. | ||
| + | |||
| + | 4. ÁBRA | ||
| + | |||
| + | A vékonyrétegek meander formában helyezkednek el, a momentumok $H_x$ irányban szeretnek beállni, és az áram a Wheatstone híd megfelelő karjaiban ±45°-os fokos szögben folyik. | ||
| + | A szenzor működésével kapcsolatban fontos megjegyezni az ún. átfordulás (flipping) jelenségét. A mágnesezettség a vékony csíkok iránya által kijelölt $H_x$ iránnyal párhuzamosan szeretnek beállni, de ezen belül egyaránt állhatnak $H_x$ és $-H_x$ irányban is. A szenzor megbízható működéséhez elengedhetetlen hogy a momentumok egységesen $H_x$ vagy egységesen $-H_x$ irányban álljanak. Különböző irányban álló momentumok esetén a szenzort fel kell mágnesezni egy megfelelő nagyságú $H_x$ irányú külső mágneses térrel. Egy $H_x$ irányban mágnesezett szenzor momentumait átfordíthatjuk $-H_x$ irányba egy megfelelő nagyságú $-H_x$ irányú külső mágneses térrel, viszont ha az átfordításhoz nem használunk elegendő nagyságú teret, a momentumoknak csak egy része fordul át. (A momentumok részleges átfordulása túlzottan nagy $H_y$ irányú külső tér hatására is előfordulhat.) | ||
| + | A mérés során a magnetorezisztív szenzorok karakterisztikáit LoggerPro számítógépes adatgyűjtő rendszer segítségével vizsgáljuk. A szenzorok egy kisméretű, függvénygenerátorral meghajtható tekercsben vannak elhelyezve, mely a 10A szenzor esetén az y, a 10A1 szenzor esetén az x irányú teret tudja változtatni. A kisméretű tekercset egy nagyobb, DC tápegységgel meghajtható tekercsbe helyezzük, mely merőleges irányú teret biztosítja. | ||
| + | A szenzorkarakterisztikák meghatározásán kívül elektronikus iránytűt készítünk. A föld mágneses terének mérésekor a szenzort ún. flipping üzemmódban használjuk, azaz az egymást követő mérések között a szenzor mágnesezettségét átfordítjuk váltakozó előjelű $H_x$ irányú mágneses tér alkalmazásával. A mágnesezettség átfordításával a szenzor $U_{ki}$-$H_y$ karakterisztikája az 5. ábra szerint változik meg. | ||
| + | |||
| + | |||
| + | 5. ÁBRA | ||
| + | |||
| + | Ez lehetővé teszi az offszet-feszültség kiküszöbölését, mivel a hasznos jel a két $M_x$ iránnyal mért érték különbsége. Ezt a megoldást kis mágneses terek pontos érzékelésére lehet használni. | ||
| + | |||
| + | ==Óriás mágneses ellenállás jelensége== | ||
| + | |||
| + | Az óriás mágneses ellenállás jelenségének megértéséhez képzeljük el a 6. ábrán feltüntetett elrendezést. Vegyünk két mágneses vékonyréteget, melyeket egy vékony, nemmágneses réteg választ el. | ||
| + | |||
| + | |||
| + | 6. ÁBRA | ||
| + | |||
| + | A felhasznált anyagok és a nemmágneses réteg vastagságának megfelelő megválasztásával elérhető, hogy a két mágneses vékonyréteg között egy ún. antiferromágneses csatolás alakul ki, magyarul külső mágneses tér hiányában a két réteg mágnesezettsége egymással ellentétes irányú lesz. Erre az elrendezésre megfelelő nagyságú külső mágneses teret kapcsolva a két réteg mágnesezettségét beforgathatjuk egymással párhuzamos irányba. A mágnesezettség párhuzamos (parallel, P) állása esetén a LINK 6. ábrán mutatott elrendezés ellenállása lényegesen kisebb, mint az ellentétes (antiparallel, AP) beállás esetén, így külső mágneses tér alkalmazásával jelentős ellenállás-csökkenést tudunk elérni. Ezt a jelenséget hívjuk óriás mágneses ellenállásnak. A jelenséget a következő egyszerű modellel szemléltethetjük: Bontsuk fel az elektromos áramot fel illetve le spinű elektronokra. A le spinű elektronok egy felfelé álló mágnesezettségű rétegen lényegesen nehezebben haladnak át, mint egy lefelé álló mágnesezettségűn. Jelöljük egy mágneses réteg ellenállását egy bizonyos spinű elektronokra nézve $R_1$-el ha a réteg mágnesezettségi iránya megegyezik az elektronok spinirányával, illetve $R_2$-vel, ha a mágnesezettség iránya ellentétes az elektronok spinirányával. A fel és le spinű elektronokat független áramcsatornaként kezelve parallel és antiparallel mágnesezettségű rétegek eredő ellenállása a LINK 7. ábrán szemléltetett helyettesítő képpel modellezhető. | ||
| + | |||
| + | 7. ÁBRA | ||
| + | |||
| + | Fejezzük ki a fenti két ellenállást $R_1 = R+\Delta R, R_2=R-\Delta R$ alakban. Így a parallel és antiparallel beállás esetén az ellenállás: | ||
| + | |||
| + | {{eq| R_{AP} {{=}} \frac{R_1 + R_2}{2} {{=}}R \ \ ,\ \ R_p {{=}} \frac{2R_1R_2}{R_1 + R_2} {{=}}R- \frac{\Delta R^2}{R} < R_{AP} |etwas lófasz| }} | ||
| + | |||
| + | |||
| + | 8. ÁBRA | ||
| + | |||
| + | |||
| + | |||
| + | 9. ÁBRA | ||
A lap 2013. augusztus 1., 17:11-kori változata
"Nem minden macska farka tarka, csak a tarka farkú macsaka farka tarka". (Szent Györgyi Albert)
//szerkesztés alatt//
Tartalomjegyzék |
Jól ismert, hogy az elektronok az elektromos töltés mellett spinnel is rendelkeznek, mely számos érdekes jelenséget, többek között bizonyos anyagok ferromágneses viselkedését eredményezi. A mindennapjainkat meghatározó elektronikai készülékek félvezető nanoszerkezetekből épülnek fel, melyek főleg az elektron töltését használják ki. Az utóbbi években azonban megjelentek újfajta, mágneses nanoszerkezetekből épülő eszközök is, melyek működési elve az elektronok kétféle spinbeállási lehetőségén alapul. Az elektronok spin szabadsági fokának használata a nanotechnológiai fejlesztések egyik legperspektivikusabb, dinamikusan fejlődő ága, melyet spin-elektronika, vagy röviden spintronika néven szoktak emlegetni. A spintronika fontosságát jellemzi, hogy a 2007. évi fizikai Nobel díjat egy ilyen elven működő jelenség, az úgynevezett óriás mágneses ellenállás (giant magnetoresistance, GMR) felfedezéséért ítélték oda. A GMR jelenségét Peter Grünberg német ill. Albert Fert francia kutatócsoportja 1988-ban egymástól függetlenül fedezték fel. Ez az alapkutatási felfedezés hamarosan komoly ipari felhasználást talált, a GMR jelenség tette lehetővé a merevlemezek tárolókapacitásának rohamos fejlődését a hagyományos, mágneses indukción alapuló olvasó fejet alkalmazó merevlemezekhez képest. Ezen kívül napjaink számos spintronikai fejlesztése, pl. az ún. mágneses RAM (MRAM) a GMR jelenségén alapul.
A mérési gyakorlaton két spintronikához kapcsolódó jelenséggel ismerkedünk meg, az ún. anizotróp mágneses ellenállás (anisotrope magnetoresistance, AMR) illetve a 2007-es Nobel díjhoz kapcsolódó óriás mágneses ellenállas (GMR) jelenségével. Az AMR jelenséget PHILIPS KMZ10A, KMZ10A1 típusú magnetorezisztív szenzorokon, még a GMR jelenséget a Központi Fizikai Kutatóintézet Fémfizikai Csoportja Co-Cu rétegszerkezeteken tanulmányozzuk.
Anizotróp mágneses ellenállás elvén működő magnetorezisztív szenzorok
Egy mágneses anyagban a kristálytani irányok, illetve az anyag geometriája által kitüntetett irányok úgynevezett mágneses anizotrópiát okozhatnak, melynek hatására a mágneses momentumok az anizotrópia által kitüntetett, ún. könnyű mágnesezési irányba állnak be. A mérés során Phillips KMZ10A ill. KMZ10A1 típusú magnetorezisztív szenzorokat használunk. A szenzorok mágneses vékonyrétegekből készült keskeny mágneses csíkokból épülnek fel, melyekben a geometriai anizotrópia miatt zérus külső tér esetén a mágneses momentumok a csíkkal párhuzamosan szeretnek állni. Véges külső mágneses tér alkalmazásával a momentumokat elfordíthatjuk a kitüntetett irányhoz képest. A spin-pálya kölcsönhatáson alapuló bonyolult fizikai folyamatok miatt egy mágneses vékonyréteg ellenállása függ a mágneses momentumok és az áramirány által bezárt 
szögtől, melyet anizotróp mágneses ellenállás (AMR) jelenségének nevezünk.
Egy egyszerű magnetorezisztív mintán az LINK 1. ábra szerinti elrendezésben az ellenállás az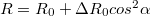 
képlettel közelíthető. Ha a könnyű mágnesezési irányra merőleges mágneses teret alkalmazunk, a momentumok elfordulnak a mágneses anizotrópia által kitüntetett irányból, így a vékonyréteg ellenállása megváltozik.
1. ÁBRA
Ha az áram a preferált mágnesezettség irányába folyik, az ellenállás négyzetes függvénye lesz a mágnesezettségnek, hiszen 
arányos a külső térrel. Lineáris szenzorkarakterisztikát egy speciális elrendezéssel, az ún. Barber-pole segítségével érhetünk el LINK (2. ábra). Ha a mágneses vékonyrétegből egy hosszú keskeny csíkot készítünk, a mágnesezettség a hosszirányba fog beállni. A csík két vége között folyó áram irányát a vékonyréteg tetejére ferde csíkokban felpárologtatott alumíniumrétegek segítségével forgatjuk el. Az alumíniumrétegek lényegesen jobban vezetnek az alattuk levő mágneses vékonyrétegnél, ezért az elektronok "próbálják minimalizálni a vékonyrétegben töltött időt", és így a vékonyrétegben az áramirány az alumínium csíkokra merőlegesen fog beállni.
2. ÁBRA
Az áramirányt 45°-al elforgatva a mágnesezettséghez képest lineáris szenzorkarakterisztikát kaphatunk, hiszen a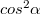 
függvény lineáris szakaszát használjuk.
A hőmérsékleti drift elkerülése érdekében a szenzor 4 db, hídkapcsolásban elhelyezett magnetorezisztív vékonyrétegből áll LINK(3. ábra). A híd két szemközti csúcsára 5V tápfeszültséget kötünk, és a másik két szemközti csúcs között mérjük a feszültséget. Zérus mágneses térben a híd kiegyenlített, így a kimeneten ideális esetben zérus feszültség látható. Véges mágneses térben a térrel arányos, tipikusan mV-os nagyságrendű jelet tapasztalunk. A szenzorokban a mágnesezettség az ábrán jelölt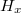 
irányban áll, így 
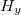irányú mágneses teret tudunk mérni. A KMZ10A és KMZ10A1 szenzorok közötti különbség, hogy a 10A szenzorban a preferált mágnesezési irány a forrasztólábakra merőleges irányú, míg a 10A1 szenzorban a forrasztólábakkal párhuzamos irányú. (Ennek megfelelően a 10A szenzor a lábakkal párhuzamos, míg a 10A1 szenzor a lábakra merőleges irányban méri a teret.)
3. ÁBRA
A szenzor valóságos elrendezését a 4. ábrán látjuk.
4. ÁBRA
A vékonyrétegek meander formában helyezkednek el, a momentumok 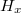irányban szeretnek beállni, és az áram a Wheatstone híd megfelelő karjaiban ±45°-os fokos szögben folyik.
A szenzor működésével kapcsolatban fontos megjegyezni az ún. átfordulás (flipping) jelenségét. A mágnesezettség a vékony csíkok iránya által kijelölt 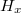iránnyal párhuzamosan szeretnek beállni, de ezen belül egyaránt állhatnak 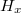és 
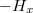irányban is. A szenzor megbízható működéséhez elengedhetetlen hogy a momentumok egységesen 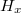vagy egységesen 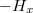irányban álljanak. Különböző irányban álló momentumok esetén a szenzort fel kell mágnesezni egy megfelelő nagyságú 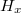irányú külső mágneses térrel. Egy 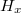irányban mágnesezett szenzor momentumait átfordíthatjuk 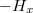irányba egy megfelelő nagyságú 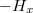irányú külső mágneses térrel, viszont ha az átfordításhoz nem használunk elegendő nagyságú teret, a momentumoknak csak egy része fordul át. (A momentumok részleges átfordulása túlzottan nagy 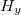irányú külső tér hatására is előfordulhat.)
A mérés során a magnetorezisztív szenzorok karakterisztikáit LoggerPro számítógépes adatgyűjtő rendszer segítségével vizsgáljuk. A szenzorok egy kisméretű, függvénygenerátorral meghajtható tekercsben vannak elhelyezve, mely a 10A szenzor esetén az y, a 10A1 szenzor esetén az x irányú teret tudja változtatni. A kisméretű tekercset egy nagyobb, DC tápegységgel meghajtható tekercsbe helyezzük, mely merőleges irányú teret biztosítja.
A szenzorkarakterisztikák meghatározásán kívül elektronikus iránytűt készítünk. A föld mágneses terének mérésekor a szenzort ún. flipping üzemmódban használjuk, azaz az egymást követő mérések között a szenzor mágnesezettségét átfordítjuk váltakozó előjelű 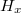irányú mágneses tér alkalmazásával. A mágnesezettség átfordításával a szenzor 
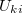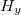- karakterisztikája az 5. ábra szerint változik meg.
5. ÁBRA
Ez lehetővé teszi az offszet-feszültség kiküszöbölését, mivel a hasznos jel a két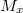 
iránnyal mért érték különbsége. Ezt a megoldást kis mágneses terek pontos érzékelésére lehet használni.
Óriás mágneses ellenállás jelensége
Az óriás mágneses ellenállás jelenségének megértéséhez képzeljük el a 6. ábrán feltüntetett elrendezést. Vegyünk két mágneses vékonyréteget, melyeket egy vékony, nemmágneses réteg választ el.
6. ÁBRA
A felhasznált anyagok és a nemmágneses réteg vastagságának megfelelő megválasztásával elérhető, hogy a két mágneses vékonyréteg között egy ún. antiferromágneses csatolás alakul ki, magyarul külső mágneses tér hiányában a két réteg mágnesezettsége egymással ellentétes irányú lesz. Erre az elrendezésre megfelelő nagyságú külső mágneses teret kapcsolva a két réteg mágnesezettségét beforgathatjuk egymással párhuzamos irányba. A mágnesezettség párhuzamos (parallel, P) állása esetén a LINK 6. ábrán mutatott elrendezés ellenállása lényegesen kisebb, mint az ellentétes (antiparallel, AP) beállás esetén, így külső mágneses tér alkalmazásával jelentős ellenállás-csökkenést tudunk elérni. Ezt a jelenséget hívjuk óriás mágneses ellenállásnak. A jelenséget a következő egyszerű modellel szemléltethetjük: Bontsuk fel az elektromos áramot fel illetve le spinű elektronokra. A le spinű elektronok egy felfelé álló mágnesezettségű rétegen lényegesen nehezebben haladnak át, mint egy lefelé álló mágnesezettségűn. Jelöljük egy mágneses réteg ellenállását egy bizonyos spinű elektronokra nézve 
-el ha a réteg mágnesezettségi iránya megegyezik az elektronok spinirányával, illetve 
-vel, ha a mágnesezettség iránya ellentétes az elektronok spinirányával. A fel és le spinű elektronokat független áramcsatornaként kezelve parallel és antiparallel mágnesezettségű rétegek eredő ellenállása a LINK 7. ábrán szemléltetett helyettesítő képpel modellezhető.
7. ÁBRA
Fejezzük ki a fenti két ellenállást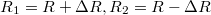 
alakban. Így a parallel és antiparallel beállás esetén az ellenállás:
![\[ R_{AP} = \frac{R_1 + R_2}{2} =R \ \ ,\ \ R_p = \frac{2R_1R_2}{R_1 + R_2} =R- \frac{\Delta R^2}{R} < R_{AP} \]](/images/math/3/5/0/350f1b6e3e4388df15ae3ebbd37a2ca4.png)
8. ÁBRA
9. ÁBRA
