„Holográfia” változatai közötti eltérés
(→Reflexiós (látvány-) hologram készítése) |
(→Elmozdulásmező vizsgálata real-time holografikus interferometriával reflexiós elrendezésben) |
||
| 111. sor: | 111. sor: | ||
Az előző mérési feladattal lényegében megegyező elrendezést kell itt is használni, mindössze a tárgyat kell kicserélni a laborban található középen megnyomható membránra, és annak felületére merőleges megvilágításra van szükség. A merőlegességet a (7) képlet alkalmazásánál fogjuk felhasználni. A membrán közepét egy mikrométerorsó nyomja, mely $10$ mikronos osztású, és $0,5\,\text{mm}$ egy fordulata. Ezt az orsót egy hozzá rögzített karon keresztül forgatjuk, melynek végét egy ugyanilyen orsó mozgatja. Mérje meg, hogy milyen hosszú a „külső“ orsó karja, azaz hol érinti azt a „belső“ orsó tengelyétől számítva, és határozza meg, hogy a külső orsó egy fordulata mennyivel nyomja meg a membrán közepét. | Az előző mérési feladattal lényegében megegyező elrendezést kell itt is használni, mindössze a tárgyat kell kicserélni a laborban található középen megnyomható membránra, és annak felületére merőleges megvilágításra van szükség. A merőlegességet a (7) képlet alkalmazásánál fogjuk felhasználni. A membrán közepét egy mikrométerorsó nyomja, mely $10$ mikronos osztású, és $0,5\,\text{mm}$ egy fordulata. Ezt az orsót egy hozzá rögzített karon keresztül forgatjuk, melynek végét egy ugyanilyen orsó mozgatja. Mérje meg, hogy milyen hosszú a „külső“ orsó karja, azaz hol érinti azt a „belső“ orsó tengelyétől számítva, és határozza meg, hogy a külső orsó egy fordulata mennyivel nyomja meg a membrán közepét. | ||
| − | A real-time interferogram készítéséhez a membránról reflexiós hologramot kell készíteni az előző mérési feladattal megegyező módon. Ezután nem szabad semmit elmozdítani! Mivel a holografikus rács már ilyenkor is diffraktál, a membránt részben a referencia és részben a tárgyhullám világítja meg (azaz a saját virtuális képe). Továbbra is sötétben lassan tekerjen a külső orsón | + | A real-time interferogram készítéséhez a membránról reflexiós hologramot kell készíteni az előző mérési feladattal megegyező módon. Ezután nem szabad semmit elmozdítani! Mivel a holografikus rács már ilyenkor is diffraktál, a membránt részben a referencia és részben a tárgyhullám világítja meg (azaz a saját virtuális képe). Továbbra is sötétben lassan tekerjen a külső orsón néhány egész fordulatot, és közben figyelje a membrán felületét a hologramlemezen keresztül. A növekvő deformációval egyre sűrűbb csíkrendszer áll elő, amely a membrán alap és deformált állapota közötti interferencia eredményeképp jön létre. Ez a real-time interferogram. Két-három különböző mértékben benyomott állapotban rögzítse az orsó tekeréseinek számát, és számlálja le a hozzá tartozó csíkszámot a membrán felületén $\frac 14$ csík pontossággal, majd a mérés kontúrtávolságával (lásd korábbi interferométeres mérések) szorozva állapítsa meg a membrán közepén fellépő legnagyobb elmozdulás névleges(mikrométerről leolvastható) és mért (interferogramról leolvasható) értékeit. Ha a leolvasások végeztével kicsit elmozdítja akár a tárgyat, akár a hologramlemezt, mit tapasztal? Mit árul el a csíkrendszer alakja az elmozdulásmezőről? Értelmezze a látottakat. |
</wlatex> | </wlatex> | ||
| − | |||
| − | |||
=== Holografikus tükör készítése === | === Holografikus tükör készítése === | ||
A lap 2013. szeptember 13., 12:36-kori változata
Tartalomjegyzék |
Bevezetés
Mint az közismert, az ember térbeli látással rendelkezik. Ez részben abból adódik, hogy két szemmel sztereo látásra van módunk, azaz testünk vagy szemünk mozgatása nélkül is korábbi tapasztalataink alapján el tudjuk helyezni a térben az érzékelt tárgyakat, mivel két szemünk eltérő képet lát. Azonban még egy szemmel is lehetőségünk van bizonyos mértékben a térbeliség megítélésére, hiszen a különböző távolságban található tárgyakat csak akkor látjuk élesen, ha szemünk ún. akkomodációs, fókuszállítási képességét használjuk. Különböző távolságokra fókuszálva, és figyelve a tárgyak képének változását ezen a módon is térbeli képet alkothatunk környezetünkről. Tehetjük ezt annak ellenére, hogy érzékelőnk - a szem retinája - csak kétdimenziós.
Az általunk látottak rögzítésének egyik elterjedt módja a fényképezés. Ekkor a látáshoz hasonlóan a valóságos tárgyakat egy kétdimenziós felületre képezzük valamilyen optikai rendszer segítségével. Ha az elkészült fényképet nézzük, akkor a valóság szemléléséhez képest még két szemmel sem látunk ahhoz hasonló térbeli hatást. Ha különböző távolságokra fókuszálunk, legfeljebb a fényképet láthatjuk életlenül. A fénykép tehát kevesebb információt tartalmaz, mint amiről készítettük, a valóságban rendelkezésre álló információk egy része nem rögzült.
A hiányzó információ pedig nem más, mint a fény fázisa, ugyanis az érzékelők, detektorok csak a fény intenzitását észlelik. A holográfia újítása - amelyet Gábor Dénesnek köszönhetünk (1947), és amelyért Nobel-díjat kapott (1971) - éppen az, hogy közvetett módon mégis lehetővé teszi egy hullám fázisának rögzítését annak ellenére, hogy a holográfia is a fotónegatívokéhoz hasonló elvű képrögzítést alkalmaz. A holográfia „trükkje”, hogy a fázisváltozást intenzitásváltozássá változtatja/kódolja, azaz a detektorok számára is érzékelhetővé teszi. A kódolás megvalósítására az interferencia jelensége alkalmas, amelynél az eredő kép intenzitásának ingadozásai az interferáló fényhullámok fáziskülönbségétől függenek. A megvalósításhoz tehát a rögzítendő tárgyról kiinduló hullámon kívül egy másik hullámra is szükség van. A siker további feltételei, hogy a két hullám interferenciaképes legyen, ehhez nagy koherenciájú fényforrásokra (lézerekre) van szükség, valamint hogy az érzékelő felbontása elegendően nagy legyen ahhoz, hogy az interferenciaképet rögzíteni tudja. De mire jó egy ilyen interferenciamező? Amint azt alább látni fogjuk, a kidolgozott hologramlemez megfelelően megvilágítva a diffrakció révén úgymond rekonstruálja a kérdéses tárgyról szórt fény intenzitás és fáziseloszlását egyaránt, így a látvány teljesen háromdimenziós lesz. A hullámok fázisának rögzítése azonban nem csak érdekes látványt eredményezhet, hanem jónéhány optikai mérési eljárást is lehetővé tesz.
Jelen mérés célja: négy kisebb méretű és eltérő típusú hologram készítésén keresztül elsajátítani a hagyományos (analóg) holográfia gyakorlati alapjait, és megismerkedni két konkrét méréstechnikai alkalmazással: a holografikus interferometriával és a holografikus optikai elemek fogalmával.
Elméleti összefoglaló
Transzmissziós hologram készítése és rekonstrukciója
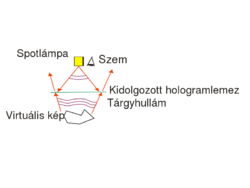
Az ún. fehérfényű látványhologramok szemlélésnek elrendezése nagyjából mindenki előtt ismert kiállítások révén: a kidolgozott hologramlemezt erős pontszerű fényforrással világítják meg, pl. spotlámpával. Azonban történetileg nem ez a hologramtípus az első, és az alapjelenség illetve a készítés megértéséhez sem ez a legalkalmasabb típus.
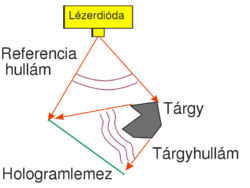
Hologram készítésének egyik lehetséges elrendezését mutatja az 1/a. ábra. Ezzel az elrendezéssel ún. transzmissziós off-axis hologram készíthető. Fényforrásnak lézerdiódát használunk, mely nagyfokú koherenciája révén biztosítja az interferenciaképességet. Ehhez továbbá ki kell zárni más természetes és hagyományos fényforrásokat, tehát a tárgyat külön meg kell világítani a lézerfénnyel. A diódalézer fénye nyalábformáló előtétlencse nélkül kb. ellipszis keresztmetszetű nyalábként tágul (divergens), így a tárgy- és referenciahullám úgy hozható létre, hogy a nyaláb egy része közvetlenül, a másik fele pedig a tárgyról szóródva jut a hologramlemezre, és ott interferálnak.
 |
 |
 |
Ez a negatív filmektől eltérően többnyire szilárd hordozóra (pl. üveglap) felvitt nagy felbontású fényérzékeny réteget jelent. A hologramlemezek térbeli felbontása egy-két nagyságrenddel nagyobb, mint a színes negatív filmeké! Az interferenciakép, az ún. holografikus rács akkor rögzíthető jó minőségben, ha a két találkozó hullám intenzitásának aránya, valamint együttes intenzitásuk, és az exponálás ideje is megfelelő. Mivel az expozíciós idők másodperc vagy perc nagyságrendűek is lehetnek, arról is gondoskodni kell, hogy az interferenciakép és a hologramlemez egymáshoz képest ne mozogjon/rezegjen, ezért az egész elrendezést speciális optikai asztalra szokás helyezni, amely rezgésmentes, és kellő merevségű, valamint más zavaró hatásokat is ki kell zárni (pl. légáramlatok, háttérfény). Érdemes megjegyezni, hogy az 1/a. ábrán látható elrendezésben nem található a fényképezésnél vagy a látásnál meglévő leképező lencse. Ez azt is jelenti, hogy egy-egy tárgypontról a hologramlemez egészére szóródik fény, nincs tehát 1-1 megfeleltetés („leképezés“) a tárgypontok és a fényérzékeny lemez pontjai között (mint a hagyományos fényképezésnél). Mivel ebben az elrendezésben a tárgy és a referencia hullám jelentős szöget zár be egymással, ezért hívjuk off-axis hologramnak.
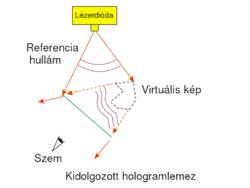
Az így exponált hologramlemezt típusától függően esetleg még elő is kell hívni, ami egy többlépéses vegyi kidolgozás, ezáltal rögzül rajta tartósan a kép. Ezen a képen azonban eltérően egy fényképtől önmagában nem látható semmi, ami az eredeti tárgyra hasonlítana, pl. egy negatív kicsinyített képmás, mint a fényképezésnél. Ez nem is csoda, hiszen a tárgy felől érkező hullámot a referenciával módosítottuk, és leképezést sem alkalmaztunk. A megfelelő kép előállításához egy másik lépésre, a hologram rekonstrukciójára van szükség, ami amolyan „dekódolás” is: ez látható az 1/b. ábrán. Az elrendezésből a tárgyat elhagyva csak a referencia hullám jut a lemezre, és ott diffraktálódik a létrejött rácsozaton, mivel azon a kidolgozás módjától és a lemez típusától függően vagy sötét és világos részek váltják egymást (amplitúdó hologram), vagy kisebb és nagyobb törésmutatójú részek (fázis hologram).
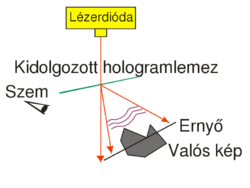
A tárgy virtuális térbeli képe (amely ernyőn nem fogható fel) annak eredeti helyén jelenik meg, ha a lemez másik oldaláról szemlélődünk, továbbá ideális esetben azonos méretben és irányításban látható. Különböző irányokból másként látszik, tehát két szemmel nézve sztereo képet ad. A különböző mélységben található részekre rá lehet fókuszálni szemmel, így a térbeli mélysége is megvan. Azonban van néhány korlátozó eltérés is: mivel mind a hologram rögzítéséhez, mind a rekonstrukcióhoz monokromatikus lézer fényforrást kell használni, a holografikus kép eredendően egyszínű, valamint a sík hologramlemez véges mérete miatt a virtuális tárgy többnyire nem járható körbe, a lemez mérete korlátozó ablakot jelent. Mivel a szemünkbe az ábra elrendezése szerint jutó fény áthaladt a lemezen (a referencia megvilágítás a lemez másik oldalán van, mint a szem), ezért ez a virtuális kép transzmissziós. A diffrakció révén azonban létrejön egy a rajzon fel nem tüntetett valós (ernyőn felfogható) kép is a lemez átellenes oldalán, amely így szintén transzmissziós. Mivel a hologram off-axis, a kétféle kép nyalábja különböző irányba terjed. Ha a valós képet jól kivehető módon szeretnénk megfigyelni, az 1/c. ábrán látható rekonstrukciós elrendezését használhatjuk. Ekkor egy keskeny lézersugárral világítjuk át a hologramlemez valamely kis darabját, és a geometriát úgy választjuk meg, hogy a megvilágító lézersugár a hologramlemezhez képest pont azzal az iránnyal ellentétes irányban haladjon, amelyben a felvételkor használt referencianyaláb érte a lemezt.
A holográfia elvi háttere
Az eredeti tárgyhullám másának visszanyerése matematikailag az alábbi egyszerű módon látható be amplitúdó hologram esetére. Tekintsük a fényhullám amplitúdóját a hologramlemez közvetlen környezetében. Felvételkor a lemezhez érkező két hullám komplex amplitúdója legyen az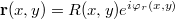 
referencia, és a 
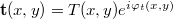tárgyhullám, ahol R és T valós értékű amplitúdók. A referenciahullám R(x,y) erőssége a lemeznél már csak lassan változik, gyakorlatilag R állandónak tekinthető. A lemezt exponáló intenzitáseloszlás, azaz interferenciakép
![\[I_{\rm{exp}}=|\mathbf{r}+\mathbf{t}|^2 = R^2+T^2+\mathbf{rt^*+r^*t}\]](/images/math/9/0/4/904fdde1a2a5e8928797ee7464e03efb.png)
a komplex konjugálást jelöli. Ideálisnak tekintett, lineáris átvitelű hologramlemez esetén a kidolgozott lemez feketedése ennek állandószorosa lesz, így a lemez 
fényáteresztő képessége ![\[\tau=1–\alpha I_{\rm{exp}}\]](/images/math/f/8/c/f8c015eb9fbca79092b776d656dffdcc.png)
alakú, ahol 
egy anyagállandó és az expozíciós idő szorzata. Rekonstrukciókor a hologramlemezt az eredeti referenciahullámmal átvilágítva közvetlenül a lemez mögött a komplex amplitúdó
![\[\mathbf{a} = \mathbf{r}^*\tau=\mathbf{r}(1–\alpha R^2–\alpha T^2)–\alpha\mathbf{r}^2\mathbf{t}^*–\alpha R^2\mathbf{t}\]](/images/math/d/7/7/d7737d2dff57b5e0ff6b8f28c5b33c5d.png)
alakot ölt. Ennek első tagja a referenciahullám áthaladó hányada, második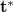 
-al arányos tagja egy fókuszálódó (ez 
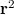miatt lehet) konjugált kép, harmadik t-vel arányos tagja pedig az eredeti tárgyhullám mása (vegyük észre, hogy az arányossági tényezők mind valós állandók!). Ez virtuális képet ad, mivel közvetlenül a hologramlemez mögötti síkdarabon így ugyanolyan hullámtér áll elő (fázisát is tekintve, hisz t komplex), mint az eredeti tárgyról érkező fény esetén. A (3) összefüggést épp ezért a holográfia alapegyenletének is nevezik. Off-axis hologram esetén ez a három elhajlási rend (
és 
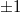) irányban szétválik, ellenkező esetben viszont nem. (Megjegyzés: ha a lemez viselkedése nem teljesen lineáris, megjelenhetnek magasabb diffrakciós rendek is)
Reflexiós hologram készítése és rekonstrukciója
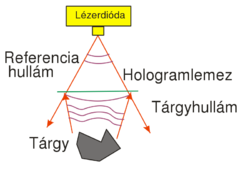
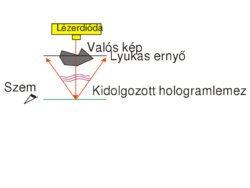
A fejezet elején említett fehérfényű látványhologramok az eddig tárgyalt típustól abban térnek el, hogy in-line elrendezésűek, azaz a nyalábok a lemez normálisával nulla vagy kis szöget zárnak be, valamint reflexiós elrendezésűek: a referencia és a tárgynyaláb a lemez átellenes oldaláról érkezik, rekonstrukciókor pedig a megvilágítás és a megfigyelés van azonos oldalon. A reflexiós hologramok rögzítésének elrendezését a 2/a. ábra mutatja. Ilyen hologramok esetén is megfigyelhető valós és virtuális rekonstruált kép, az ezekhez tartozó elrendezés a 2/b. és 2/c. ábrán látható.
 |
 |
 |
Fehér fényben ezek a hologramok azért tekinthetők meg, mert kb.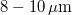 
vagy még vastagabb fényérzékeny réteget tartalmazó lemezre készülnek, így már ún. vastag hologramnak tekinthetők a hullámhosszhoz képest. A vastag diffrakciós rácsok ún. Bragg-effektust mutatnak: a fehér fényt alkotó hullámokból csak a rögzítésnél használthoz közeli hullámhosszakon diffraktálnak jelentősen, így „szelektálnak” a színek között, továbbá érzékenyek a rekonstrukciónál alkalmazott megvilágítás irányára is, amelynek nagyjából azonosnak kell lennie a felvételkori referencia nyaláb irányával, ez pedig egy irányszelektivitást jelent. Ez utóbbi tulajdonságnak köszönhetően vastag hologramlemezbe többet is lehet exponálni úgy, hogy a rögzített képek közül lényegében mindig csak egy rekonstruálódik a megvilágítás irányától függően. (Minél vastagabb, „térfogatibb” egy hologram, annál szelektívebb, így szélsőséges esetben rengeteg hologram - vagyis kép, azaz akár bináris adat - rögzíthető a fényérzékeny anyag egyazon térfogatába. Ez az alapja a holografikus adattárolásnak.)
Holografikus interferometria
Mivel a rekonstruált tárgyhullám komplex amplitúdóját maga az eredeti tárgy határozza meg, pl. annak alakja, felületi minősége, így a hologram ezekről is tárol valamennyi információt. Ha egyetlen tárgyról annak két különböző állapotában készítünk egy-egy hologramot ugyanarra a lemezre egymás után azonos referenciával, az így kapott lemezt kétexpozíciós hologramnak hívjuk:
![\[I_{12}=|\mathbf r+\mathbf t_1|^2+|\mathbf r+\mathbf t_2|^2=R^2+T^2+\mathbf r\mathbf t_1^*+\mathbf r^*\mathbf t_1+R^2+T^2+\mathbf r\mathbf t_2^*+\mathbf r^*\mathbf t_2=2R^2+2T^2+(\mathbf r\mathbf t_1^*+\mathbf r\mathbf t_2^*)+(\mathbf r^*\mathbf t_1+\mathbf r^*\mathbf t_2)\]](/images/math/0/0/7/0078c0b66dacd94102d005e54b295c25.png)
(Itt feltételeztük, hogy a tárgynyalábnak csak a fázisa változott meg érdemben, T valós amplitúdója nem, továbbá az indexek az állapotokat jelölik.) Rekonstrukciókor a két állapot egyidejűleg jelenik meg:
![\[\mathbf a_{12}=\mathbf r\tau=\mathbf r(1-\alpha I_{12})=\mathbf r(1-2\alpha R^2-2\alpha T^2)-\alpha \mathbf r^2(\mathbf t_1^*+\mathbf t_2^*)+\alpha R^2(\mathbf t_1+\mathbf t_2)\]](/images/math/8/7/d/87ddc9647964e179953751d45f3d011d.png)
azaz az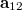 
hullámtérben egy 
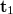-el és egy 
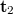-vel arányos tag is szerepel mindkét első elhajlási rendben, amelyek a képeket adják. Ha a virtuális képet szemléljük, ott csak az utolsó 
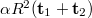tagoknak van járuléka, hisz a többi rend „máshová” terjed, így az 
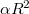arányossági tényezőktől eltekintve a megfigyelhető intenzitás ebben a diffrakciós rendben az alábbi:
![\[I_{12,\text{virt}}=|\mathbf a_{12,\text{virt}}|^2=|\mathbf t_1+\mathbf t_2|^2=2T^2+(\mathbf t_1^* \mathbf t_2+\mathbf t_1 \mathbf t_2^*)=2T^2+(\mathbf t_1^* \mathbf t_2+c.c.)\]](/images/math/9/4/f/94f5caf469c66f3743dd11c3b159cc5f.png)
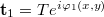és 
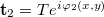, így ![\[\mathbf t_1^*\mathbf t_2=T^2e^{i[\varphi_2(x,y)-\varphi_1(x,y)]},\]](/images/math/1/d/a/1da9f8fae36674a1795aeb6b666ca89a.png)
![\[2T^2\cos[\varphi_2(x,y)-\varphi_1(x,y)]\]](/images/math/c/5/2/c524dd642789e50faaf392bad825e5de.png)
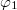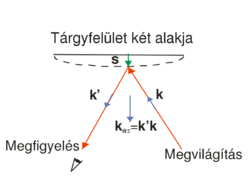
ill.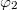 
fázisokat a 3. ábra alapján felírva belátható, hogy a különbségüket a ![\[\Delta\varphi=\varphi_2-\varphi_1=\vec s\cdot(\vec k'-\vec k)=\vec s\cdot\vec k_\text{érz}\]](/images/math/c/8/3/c83eebe27841e839b8806f7099c6f0a0.png)
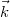a tárgyat megvilágító síkhullám hullámvektora, 
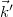pedig a tárgyról a megfigyelés irányába kiinduló nyaláb hullámvektora (
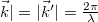), valamint 
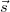az elmozdulásvektor és 
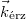az úgynevezett érzékenységi vektor. Az ábrán a piros nyilak önkényesen kiragadott sugarak a kiterjedt nyalábból. Mivel általános esetben az elmozdulásvektor a felület különböző részein nem állandó, a fáziskülönbség is helyfüggő lesz. A skaláris szorzásból látható, hogy az s vektornak csak az érzékenységi vektor irányú komponense számít, azaz csak az mérhető. Az érzékenységi vektor iránya és hossza is változtatható, ha a megvilágítás illetve a megfigyelés (szemlélés) irányát változtatjuk, így pl. ha mozgunk egy kétexpozíciós hologram előtt, a csíkrendszer is mozog, változik, mivel a fáziskülönbség is változni fog.
A fentiekhez hasonló, a tárgy megváltozását kontúrozó interferenciacsíkokat lehet látni akkor is, ha csak egyet exponálunk a tárgyról, a kidolgozott hologramlemezt tized-mikrométeres pontossággal (!) visszahelyezzük az erre alkalmas tartóba, majd a tárgyat továbbra is az eredeti nyalábokkal megvilágítva deformáljuk. Ekkor az eredeti állapot képe interferál a megváltozott állapot élő képével, így ahogy változik a deformáció, úgy változnak az interferenciacsíkok is. Ennek az igen látványos módszerenek a neve real-time holografikus interferometria, és mutatja, hogy megfelelő technológia mellett a fázishelyes fényhullám rekonstrukciót mennyire komolyan lehet venni.
Holografikus optikai elemek
Ha a tárgyhullám és a referenciahullám egyaránt síkhullám, amelyek valamilyen szöget zárnak be, a hologramon rögzülő interferenciakép egyszerű, ekvidisztáns egyenes csíkokból álló rács lesz. Az ilyen diffrakciós rácsot tekinthetjük a legegyszerűbb példának a holografikus optikai elemekre (HOE-kre). A holografikus úton létrehozott rács előnye, hogy egyszerűen előállítható, nagyon jó hatásfokú diszperzív elemet szolgáltat spektroszkópiai alkalmazásokhoz. Természetesen a rácsállandó a két síkhullám hullámhosszának és bezárt szögének függvényében pontosan beállítható. Komplexebb feladatokat ellátó (pl. helyfüggő rácsállandójú vagy fókuszáló) diffrakciós rácsokat is egyszerűen előállíthatunk holografikus úton: mindössze a két interferáló síkhullám egyikét kell kicserélnünk alkalmasan megtervezett hullámfrontú hullámra.
Mivel a hologram által rekonstruált kép olyan, mintha a tárgy teljes valójában „ott lenne“, várható, hogy ha a tárgy szerepét valamilyen optikai eszköz, pl. egy lencse vagy egy tükör tölti be, akkor a hologram bizonyos korlátok között valóban úgy fog működni, mint az adott optikai eszköz, amelyről készült (tehát pl. az adott módon fókuszálni vagy reflektálni fogja a fényt). Az ilyen egyszerű holografikus lencsék vagy tükrök is a HOE-k csoportjába tartoznak.
Az alábbiakban egy konkrét példaként megnézzük, hogyan lehet két egyszerű gömbhullám interferenciájának rögzítésével holografikus lencsét előállítani. Feltételezzük, hogy mindkét gömbhullám a hologram síkjára merőleges optikai tengelyről indul ki (ezt ún. on-axis elrendezésnek nevezzük). Az egyik (nevezzük ezt a referenciahullámnak)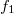 
, a másik (nevezzük ezt a tárgyhullámnak) 
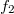távolságra a hologramtól. Ekkor – a gömbhullámok jólismert parabolikus/paraxiális közelítését alkalmazva, és mindkét hullámnál konstans egységnyi amplitudót feltételezve – a referenciahullám és a tárgyhullám (1) egyenletben szereplő 
ill.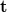 
komplex amplitudója az alábbi alakban írható a hologram síkjának (x,y) pontjában:
![\[\mathbf r=e^{i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}{2f_1}\right)},\,\mathbf t=e^{i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}{2f_2}\right)}\]](/images/math/0/a/c/0ac88ad1144539bd0b326f7b53b04b12.png)
A hologramon rögzülő interferenciakép ekkor így alakul:
![\[I=2+e^{i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}2\left( \frac 1{f_2}-\frac 1{f_1}\right)\right)}+e^{-i\frac{2\pi}{\lambda}\left(\frac{x^2+y^2}2\left( \frac 1{f_2}-\frac 1{f_1}\right)\right)}\]](/images/math/e/4/3/e433756b9bc2936117ff5f00e1fd84c6.png)
a hologram áteresztőképessége pedig ismét a (2) egyenlettel írható fel, tehát lineáris függvénye 
-nek. Rekonstruáljuk most a hologramot az referenciahullám helyett egy merőleges beesésű síkhullámmal (amelynek tehát a komplex amplitudója a hologram síkjában 
, egy valós konstans). Ekkor a (3) egyenlet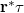 
kifejezése helyett 
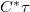szerepel, azaz egy konstans faktortól eltekintve maga a áteresztőképesség-függvény adja meg az átvilágított lemez mögött előálló fényhullám komplex amplitudóját. Ebből és a (2) és (10) egyenletekből látható, hogy a hologramból rekonstruálódó három elhajlási rend a következő lesz:
- egy konstans komplex amplitudójú merőleges síkhullám (nulladrend, a megvilágító nyaláb elhajlás nélkül továbbhaladó része),
- egy
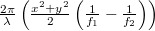fázissal leírható hullám (+1-rend),
- egy
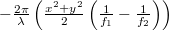fázissal leírható hullám (-1-rend).
A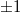 
-rendű tagok fázisának matematikai alakjából látható (emlékeztetők: a (9) képletek), hogy ezek voltaképpen olyan (paraxiális) gömbhullámok, amelyek 
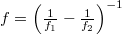, ill. 
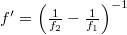távolságra fókuszálódnak a hologram síkjától. Természetesen 
és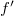 
közül az egyik pozitív, a másik negatív, tehát a 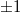-rendek közül az egyik konvergens, a másik divergens gömbhullám, mindkettő 
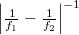fókusztávolsággal. Összefoglalva: a két on-axis gömbhullám interferenciáját rögzítő hologrammal olyan HOE-t kaptunk, amely gyűjtő- és szórólencseként is funkcionálhat, attól függően hogy egy adott alkalmazáskor melyik rekonstruált elhajlási rendet használjuk fel.
A HOE-k legfontosabb alkalmazási területeit azok az esetek jelentik, amikor bonyolult, összetett optikai manipulációkat végrehajtó elrendezések (pl. az optikai távközlésben demultiplexelésre használt sokfókuszú lencsék) helyettesítését szeretnénk megoldani egyetlen egyszerű és kompakt hologrammal. Ilyenkor a legfőbb előny a holográfia alkalmazásával elérhető méret- és költségcsökkenés.
Mérési feladatok
Reflexiós (látvány-) hologram készítése
A mérési gyakorlat első részében egy kb.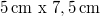 
-es hologramlemezre egy hasonló méretű erősen reflektáló, lehetőleg csillogó tárgyról készítünk fehérfényű hologramot. A fényforrás egy 
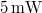névleges teljesítményű, 
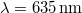hullámhosszúságú vörös fényű diódalézer, mely 
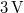táplálás mellett kb. 
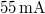áramot vesz fel, és fix befogóval rendelkezik. Ez a lézerdióda „csupasz”, így nyalábja eleve tágul. A hologramlemezek LITIHOLO RRT20 típusú, ~600-660 nm hullámhossztartományra érzékeny, ún. instant filmmel bevont üveglemezek. Az RRT20 film érzékenysége 
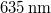-en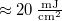 
. A fényérzékeny réteg 
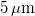-es vastagsága jóval nagyobb a megvilágító hullámhossznál, ami a 2. pontban leírtak szerint azt jelenti, hogy a használt hologramlemezek alkalmasak vastag hologramok rögzítésére. Exponáláskor az instant filmben a megvilágítás intenzitásától függő törésmutató-változás rögzül. Az interferenciakép tehát törésmutató-moduláció formájában valós időben kódolódik a film anyagában. Ennek a módszernek az az előnye, hogy exponálás után semmilyen, a hagyományos holografikus emulziók esetén használatos kémiai eljárást (előhívás, halványítás, rögzítés) nem igényel, hiszen a holografikus rács a beírás folyamán rögzül is az anyagban. A hologramlemezek fényzáró dobozban találhatók, melyet csak sötétben, közvetlenül az exponálás előtt szabad kinyitni, majd egy lemezt kiemelve rögtön visszazárni.
Kapcsolja be a lézert a tápenységnél, és állítsa össze a 2/a. ábra elrendezését. Az elemek egy része mágneses talpakon található, melyeket forgatógombbal lehet lazítani illetve rögzíteni. A többi állítási lehetőséget a szárnyas anyát használó befogások jelentik. Használja a mérőhelyen található próbalemezt és azonos méretű papírt a beállításhoz, a nyaláb követéséhez. Helyezze a tárgyat egy hasábra a megfelelő magasság eléréséhez. A lemezt speciális tartóba lehet helyezni, mely csavarokkal szorítja a lemezt a helyére. Ellenőrizze, hogy a lemez teljes felülete és a tárgy megfelelő oldala is elegendően nagy felületen árnyékmentesen meg van világítva. Helyezze a tárgyat és a lemezt a lehető legközelebb egymáshoz. Segíti a későbbi rekonstrukciót, ha a megvilágítás valamennyire ferdén felülről érkezik a függőleges helyzetű lemezre. A lemez egyik oldalán található a fényérzékeny fólia, ennek célszerű a tárgy felőli oldalra kerülnie. Ellenőrizze, hogy a rögzítések megfelelőek, nincs-e „nyitva” hagyott mágneses talp, vagy laza szárnyas anya.
Exponálás előtt mutassa meg az elrendezést a mérésvezetőnek. Jóváhagyás után megkezdődhet az exponálás. Ehhez sötétítse el a szobát, kapcsolja le a lézert (tápegységen output off), majd a mérőhelyen található kék led fényében tájékozódva vegyen ki egy lemezt a tartódobozból, és azt zárja vissza. Helyezze a lemezt a tartóba, majd kapcsolja vissza a lézert. Az exponálás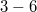 
percig tart. Ez alatt kerülni kell a zavaró fényeket, a mozgást, rezgést.
Exponálás után vegye ki a helyéről a tárgyat, és – a diódalézer fényét használva – figyelje meg a rekonstruált virtuális képet. Ezután vegye ki a tartóból a hologramot, és a folyosón található fehér fényű spotlámpával is rekonstruálja a virtuális képet. Milyen színben látható ekkor a tárgy virtuális képe? Mi látható, ha a lemezt az oldalán átfordítva nézzük? Jegyezze fel tapasztalatait!
Megjegyzés: Az előbbi feladathoz saját tárgyakat is lehet hozni, de rendelkezünk jól bevált tárgykészlettel. Alkalmas tárgyak: érmék, kulcsok, fém dísztárgyak (méretkorláttal), és arany vagy ezüst festékkel csillogóra festett egyéb tárgyak, macskaszem prizma. Korlátozottan alkalmasak fehér, sima felületű tárgyak, kis plüssfigurák (rövid szőrrel), fehér LEGO elemek.
Elmozdulásmező vizsgálata real-time holografikus interferometriával reflexiós elrendezésben
Az előző mérési feladattal lényegében megegyező elrendezést kell itt is használni, mindössze a tárgyat kell kicserélni a laborban található középen megnyomható membránra, és annak felületére merőleges megvilágításra van szükség. A merőlegességet a (7) képlet alkalmazásánál fogjuk felhasználni. A membrán közepét egy mikrométerorsó nyomja, mely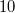 
mikronos osztású, és 
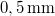egy fordulata. Ezt az orsót egy hozzá rögzített karon keresztül forgatjuk, melynek végét egy ugyanilyen orsó mozgatja. Mérje meg, hogy milyen hosszú a „külső“ orsó karja, azaz hol érinti azt a „belső“ orsó tengelyétől számítva, és határozza meg, hogy a külső orsó egy fordulata mennyivel nyomja meg a membrán közepét.
A real-time interferogram készítéséhez a membránról reflexiós hologramot kell készíteni az előző mérési feladattal megegyező módon. Ezután nem szabad semmit elmozdítani! Mivel a holografikus rács már ilyenkor is diffraktál, a membránt részben a referencia és részben a tárgyhullám világítja meg (azaz a saját virtuális képe). Továbbra is sötétben lassan tekerjen a külső orsón néhány egész fordulatot, és közben figyelje a membrán felületét a hologramlemezen keresztül. A növekvő deformációval egyre sűrűbb csíkrendszer áll elő, amely a membrán alap és deformált állapota közötti interferencia eredményeképp jön létre. Ez a real-time interferogram. Két-három különböző mértékben benyomott állapotban rögzítse az orsó tekeréseinek számát, és számlálja le a hozzá tartozó csíkszámot a membrán felületén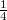 
csík pontossággal, majd a mérés kontúrtávolságával (lásd korábbi interferométeres mérések) szorozva állapítsa meg a membrán közepén fellépő legnagyobb elmozdulás névleges(mikrométerről leolvastható) és mért (interferogramról leolvasható) értékeit. Ha a leolvasások végeztével kicsit elmozdítja akár a tárgyat, akár a hologramlemezt, mit tapasztal? Mit árul el a csíkrendszer alakja az elmozdulásmezőről? Értelmezze a látottakat.
Holografikus tükör készítése
Ismételje meg az első feladatot tárgyként a mérőhelyen található kétoldalú tükröt homorú tükörként használva. Vizsgálja meg a kész holografikus tükör működését, és jegyezze fel tapasztalatait. Használja a folyosói szpotlámpákat.
Transzmissziós hologram készítése
Állítson össze transzmissziós hologram elrendezést az 1/a. ábra szerint. Ellenőrizze, hogy a lemez helyéről mi látszik a tárgyból, illetve hogy szóródik-e róla fény a lemez felé. Törekedjen arra, hogy a referencia és a tárgynyaláb egymással bezért szöge 30-45 fok körül legyen, valamint az úthosszak különbsége se legyen 10 centinél sokkal nagyobb. A lemezt úgy kell a tartóba helyezni, hogy a fóliázott rész a beérkező nyalábok felé nézzen. Az exponálást az első feladatban leírtaknak megfelelően kell végezni. A kész hologram csak lézerfényben tekinthető meg. Nézze meg az eredményt az 1/b. és az 1/c. ábrák elrendezésében is, utóbbihoz egy másik, nem táguló nyalábú lézer szükséges. Hogyan jelenik meg a holografikus kép térbelisége? Működhet-e a rekonstrukció más színű lézerrel?
Egyéb információk
A jegyzőkönyvben: elméleti bevezető nem szükséges, de saját igény esetén se legyen több 3/4 oldalnál. Foglalja össze a mérés során tapasztaltakat! Térjen ki a mérési feladatokban megfogalmazott kérdésekre is! Biztonsági tudnivalók: A lézerfénybe ne nézzünk bele, a szórt fénybe pedig legfeljebb rövid ideig.
Linkek:
Házilag karcolt egyszerű hologramok
Szertár videó karcolt hologramokról
