„Lock-in programozás, kvarcszenzor vizsgálata” változatai közötti eltérés
(→Órákban használt kvarcoszcillátor nanofizikai alkalmazása) |
(→A kvarcoszcillátor leírása egy egyszerű modellel) |
||
| 59. sor: | 59. sor: | ||
A $Q=\alpha \cdot z$ összefüggés alapján a szenzor árama az oszcillátor sebességével arányos: | A $Q=\alpha \cdot z$ összefüggés alapján a szenzor árama az oszcillátor sebességével arányos: | ||
$$I=\alpha \cdot \dot{z}.$$ | $$I=\alpha \cdot \dot{z}.$$ | ||
| − | Ezt a fenti differenciálegyenletbe hellyettesítve egy feszültséggel gerjesztett soros elektromos rezgőkör (RLC kör) differenciálegyenletét kapjuk, ahol az $L$, $R$ és $C$ elektromos paraméterek a piezoelektromos együtthatón keresztül megfeleltethetőek a $m$, $k$ és $ | + | Ezt a fenti differenciálegyenletbe hellyettesítve egy feszültséggel gerjesztett soros elektromos rezgőkör (RLC kör) differenciálegyenletét kapjuk, ahol az $L$, $R$ és $C$ elektromos paraméterek a piezoelektromos együtthatón keresztül megfeleltethetőek a $m$, $k$ és $\gamma$ mechanikai paramétereknek. |
Fontos azonban megjegyezni, hogy a kvarcosszcillátor elektródái között akkor is tapasztalnánk kapacitást, ha a kvarc nem lenne piezoelektromos, így az oszcillátor elektromos viselkedésének leírásához az RLC körrel párhuzamos $C_0$ kapacitást is figyelembe kell venni. Ezzel a kiegészítéssel, azaz a 4. ábrán látható helyettesítő képpel egészen pontosan leírható a kvarc-oszcillátor elektromos viselkedése. | Fontos azonban megjegyezni, hogy a kvarcosszcillátor elektródái között akkor is tapasztalnánk kapacitást, ha a kvarc nem lenne piezoelektromos, így az oszcillátor elektromos viselkedésének leírásához az RLC körrel párhuzamos $C_0$ kapacitást is figyelembe kell venni. Ezzel a kiegészítéssel, azaz a 4. ábrán látható helyettesítő képpel egészen pontosan leírható a kvarc-oszcillátor elektromos viselkedése. | ||
| 70. sor: | 70. sor: | ||
|} | |} | ||
| − | A fenti modell alapján számolva a kvarcoszcillátor | + | A fenti modell alapján számolva a kvarcoszcillátor komplex impedanciájának abszolút értéke a következő képlettel számítható ki: |
| − | $$|Z|=\frac{\sqrt{(A-\omega^2)^2+D^2 \omega^2}}{ | + | $$|Z|=\frac{\sqrt{(A-\omega^2)^2+D^2 \omega^2}}{E \omega \sqrt{(B-\omega^2)^2}+D^2\omega^2},$$ |
| − | ahol az alábbi paramétereket vezettük be: $A | + | ahol az alábbi paramétereket vezettük be: $A=\frac{1}{L C}$, $B=\frac{C+C_0}{C_0 C L}$, $D=\frac{R}{L}$, $E=C_0$. |
</wlatex> | </wlatex> | ||
A lap 2013. október 1., 15:57-kori változata
Tartalomjegyzék |
A mérés célja
A mérés célja a Stanford Research Systems SR830 típusú digitális lock-in erősítő használatának és programozásának megismerése, tesztmérés elvégzése egy párhuzamos LC körön, illetve egy atomerő-mikroszkópokban is használt kvarcszenzor vizsgálata.
Órákban használt kvarcoszcillátor nanofizikai alkalmazása
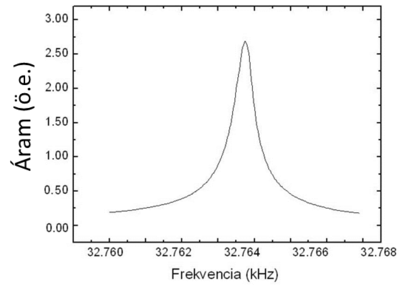
Az 1. ábrán szemléltetett kvarcoszcillátort kvarcórákban, elektronikai áramkörökben használják órajel előállítására, olcsón beszerezhető - körülbelül 20 Ft/db. Az oszcillátor egy hangvilla alakú kvarc (Tuning Fork vagy röviden TF-nek is szokták nevezni), a legfontosabb jellemzője a rezonancia-frekvenciájának az értéke, névlegesen 32,768kHz (=215 Hz).
A kvarc piezoelektromos viselkedésének köszönhetően a hangvilla rezgése elektromos feszültség segítségével gerjeszthető. Az oszcillátor természetesen több rezgési módussal is rendelkezik, azonban az elektródák úgy vannak kialakítva, hogy alapvetően azt a módust gerjesztik, melyben az ágak a hangvilla síkjában, tükörszimmetrikusan rezegnek. Ezen módus sem erővel, sem forgatónyomatékkal nem hat a rögzítési pontra, így gyengén csatolódik a külvilághoz. Ennek köszönhetően a hangvilla óriási jósági tényezővel rendelkezik.
A kontaktusokra váltakozó feszültséget kapcsolva a kristály periodikusan deformálódik, rezgésbe jön. Amikor a rákapcsolt váltakozó feszültség frekvenciája megegyezik a kvarckristály anyaga és méretei által meghatározott rezonancia-frekvenciával, a rezgési amplitúdó sokszorosára nő. A rezgés detektálásához a kvarcoszcillátoron folyó áramot mérjük, ami a hangvilla ágainak sebességével arányos, a rezonancia-frekvenciánál maximuma van (1. ábra, jobb oldal). Ez az egyszerű kvarcszenzor atomerő-mikroszkóp érzékelőjeként is kiválóan használható.
 |
 |
| 1. ábra. Kvarcórákban használt hangvilla alakú kvarcoszcillátor (bal oldal) és annak rezonancia-görbéje (jobb oldal), azaz az áram abszolút értéke a konstans amplitudójú gerjesztő feszültség frekvenciájának függvényében. Forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013. | |
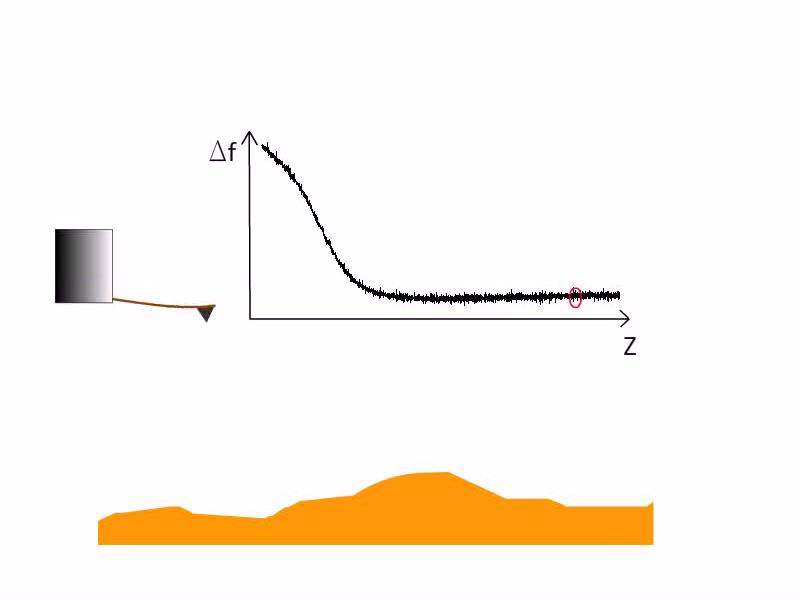
Egy hagyományos atomerő-mikroszkópban (atomic force microscope, AFM) egy laprugó végére helyeznek el egy hegyes tűt, amit közel visznek a felülethez. A laprugó mozgását egy lézer segítségével detektálják. Dinamikus üzemmódban a laprugót rezonancia-frekvenciájához közel rezgetik. A tű és a minta közötti erőhatás miatt elhangolódik a rezonancia-frekvencia. Mérés közben a tűvel x-y irányban (a minta síkjával párhuzamosan) pásztáznak, miközben z irányban úgy mozgatják a tűt, hogy a szabad rezgéshez képest mindig ugyanannyival legyen elhangolódva a rezonancia-frekvenciája, azaz pásztázás közben folyamatosan ugyanakkora erő hasson a tű és a minta között (2. ábra). (Itt érdemes megjegyezni, hogy a rezonanciafrekvencia eltolódása nem az erő nagyságával, hanem a tű és minta közötti erőhatás rugóállandójával, azaz az erő távolság szerinti deriváltjával arányos.) Így a tűvel nagyjából konstans, nanométeres nagyságrendű távolságban pásztáznak a minta fölött, és a z irányú mozgatás x-y függéséből leolvasható a minta topográfiája akár atomi felbontással.
  |
| 2. ábra. Atomerő mikroszkóp működése nem kontakt, dinamikus üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. |
Alacsonyhőmérsékleti AFM méréseknél a laprugó mozgásának optikai detektálása nagyon nehéz, így célszerűbb olyan szenzort alkalmazni, melynek mozgása csupán elektromosan detektálható. Erre kiválóan alkalmas az órákban használt kvarcoszcillátor: a hangvilla egyik ágára ragasztott tű hat kölcsön a felülettel, és az óriási jósági tényező miatt egészen kicsi erőhatás is jelentős rezonancia-frekvencia változáshoz vezet, így a tű és minta közötti erőhatás viszonylag könnyen detektálható.
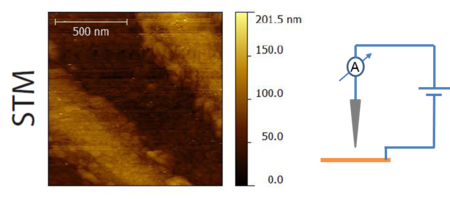
A 3. ábrán látható egy elektronsugaras litográfiával készült, majd arannyal bevont felületű nanoszerkezeten történő mérés alagútmikroszkóp üzemmódban - az alagútáramra szabályozva, majd ezt követően ugyanazon a helyen atomerő mikroszkóp üzemmódban - a kvarcoszcillátor frekvencia-eltolódására, azaz a minta és a tű között fellépő erőrhatásra szabályozva. Mindkét esetben ugyanazok a pár száz nanométer széles, párhuzamos csíkok láthatóak.
 |
|
| 3. ábra. Elektronsugaras litográfiával készült nanoszerkezeten történő mérés STM majd AFM üzemmódban, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013. |
Pásztázó szondás mikroszkópokról részletesebb információ a nanofizika tudásbázis nanoszerkezetek előállítási és vizsgálati technikái fejezetében található.
A kvarcoszcillátor leírása egy egyszerű modellel
A kvarcoszcillátor mozgását írjuk le az elképzelhető legegyszerűbb modellel, melyben egy 
effektív rugóállandójú rugóra akasztott 
effektív tömegű test mozog egy dimenzióban, z irányban. Természetesen a kvarc piezoelektromos tulajdonságait is figyelembe kell venni, amit a
![\[ \left(\begin{matrix} z \\ Q \end{matrix}\right) = \left(\begin{matrix} k^{-1} & s \\ s & C \end{matrix}\right)\cdot \left(\begin{matrix} F \\ U \end{matrix}\right)\]](/images/math/1/1/f/11f958437f7f14b356a0ec4a6acbb677.png)
mátrix-egyenlettel tehetünk meg, ahol 
az elmozdulás, 
az elektródákon megjelenő töltés, 
a kifejtett erő, 
az elektródák közötti feszültség, 
az elmozdulás egységnyi feszültség hatására terhelés nélkül (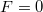
), a rugóállandó zérus feszültségnél, 
pedig a kapacitás (egységnyi feszültségre eső töltésfelhalmozódás) 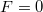mellett. Energiamegmaradási megfontolásból a fenti mátrix determinánsa 
, azaz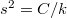 
. Ez alapján általánosan elmondható, hogy:
![\[Q=\alpha \cdot z,\]](/images/math/a/a/4/aa4a0c42e7d9d2bea5cd5b11f11bbc9d.png)
ahol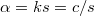 
.
Dinamikus működés leírásához a tehetetlenséget és a súrlódásból, közegellenállásból származó, sebességgel arányos csillapítást is figyelembe kell venni, így az oszcillátor elmozdulására a
![\[m\ddot{z}=-kz-\gamma\dot{z}+sU\]](/images/math/3/5/c/35c46308a83eee0adcd83ed9e55b6711.png)
differenciál-egyenlet írható fel, ahol 
a csillapítási tényező.
A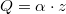 
összefüggés alapján a szenzor árama az oszcillátor sebességével arányos:
![\[I=\alpha \cdot \dot{z}.\]](/images/math/f/d/f/fdfb726cf37425b59d72dc7f394340ef.png)
Ezt a fenti differenciálegyenletbe hellyettesítve egy feszültséggel gerjesztett soros elektromos rezgőkör (RLC kör) differenciálegyenletét kapjuk, ahol az 
, 
és elektromos paraméterek a piezoelektromos együtthatón keresztül megfeleltethetőek a , és mechanikai paramétereknek.
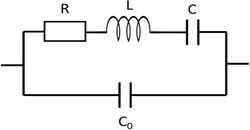
Fontos azonban megjegyezni, hogy a kvarcosszcillátor elektródái között akkor is tapasztalnánk kapacitást, ha a kvarc nem lenne piezoelektromos, így az oszcillátor elektromos viselkedésének leírásához az RLC körrel párhuzamos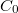 
kapacitást is figyelembe kell venni. Ezzel a kiegészítéssel, azaz a 4. ábrán látható helyettesítő képpel egészen pontosan leírható a kvarc-oszcillátor elektromos viselkedése.
 |
| 4. ábra. A kvarcoszcillátor elektromos viselkedése egy soros RLC körrel, illetve egy azzal párhuzamosan kötött 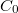kapacitással modellezhető.
|
A fenti modell alapján számolva a kvarcoszcillátor komplex impedanciájának abszolút értéke a következő képlettel számítható ki:
![\[|Z|=\frac{\sqrt{(A-\omega^2)^2+D^2 \omega^2}}{E \omega \sqrt{(B-\omega^2)^2}+D^2\omega^2},\]](/images/math/c/7/6/c762afe48c9ca497216e3a719a9dde03.png)
ahol az alábbi paramétereket vezettük be: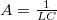 
, 
, 
, 
.
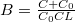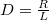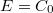Mérési feladatok
1. Áramgenerátoros meghajtással vegyük fel a mellékelt párhuzamos LC kör impedanciáját a frekvencia függvényében, határozzuk meg a rezonancia-frekvenciát, a kapacitás az induktivitás ill. az induktivitás soros ellenállásának az értékét. A mért görbét hasonlítsuk össze az elméleti várakozásokkal. A méréshez írjunk számítógépes programot, mely GPIB porton kommunikál a műszerrel. A program adott számú lépésben logaritmikus skálán változtassa a frekvenciát egy megadott kezdő és végfrekvencia között, és vegye fel a bemeneten mért jel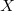 
és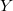 
es/vagy és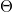 
komponensét a frekvencia függvényében. Figyeljünk az időállandó helyes beállítására!
- A lock-in erősítő kimenete feszültséggenerátorként viselkedik, azaz ha a kimenetre
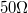-nál lényegesen nagyobb impedanciájú terhelést teszünk, akkor a kimenet az impedanciától függetlenül konstans a.c. feszültséget ad ki. Hogyan készíthetünk áramgenerátoros meghajtást megvalósító áramkört? Úgy állítsuk be a paramétereket, hogy miközben az RC-kör impedanciája változik a frekvencia függvényében, a meghajtó áram kevesebb mint 1%-ot változzon!
2. Az 1. feladatban készült mérőprogramból kiindulva vegyük fel a mellékelt tokozott kvarcoszcillátor rezonanciagörbéjét feszültséggenerátoros meghajtást használva. Az áram méréséhez ne a lock-in áramerősítő bemenetét, hanem egy soros ellenállást használjunk. Ennél a mérésnél a pontosabb frekvenciabeállítás érdekében jelforrásként egy Agilent függvénygenerátort használjunk. A lock-in generátorát az Agilent függvénygenerátorhoz szinkronizáljuk, a kvarcoszcillátorra a lock-in kimenetéről adjuk ki a jelet. Az oszcillátor meghajtásához 1:100 osztót használjunk a Lock-In 5V-os kimeneti jelszintje mellett. A mérési eredmények illesztéséből határozzuk meg az oszcillátor elektromos paramétereit, azaz , , és 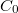értékét!
- Figyelem! A kvarcoszcillátor tönkremehet, ha a rezonanciafrekvencián túl nagy feszültséggel gerjesztjük. Ne felejtsük el az 1:100-as feszültségosztó alkalmazását!
- Ügyeljünk arra, hogy a rezonancia környékén gerjesztett oszcillátor rezgése nagyon lassan cseng le, így a frekvencia változtatásakor sokat kell várni arra, hogy az új frekvenciához tartozó állandósult állapot kialakuljon! A mért jósági tényező alapján becsüljük meg, hogy menni idő alatt cseng le a rezonáns rezgés! Kisérletileg hogyan ellenőrizhetjük a legegyszerűbben, hogy elég lassan mérünk-e, azaz hogy minden mérési pontnál csak az adott frekvencián rezeg az oszcillátor, és a korábbi gerjesztés már lecsengett?
- A rezonancia környékén érdemes nagy frekvenciafelbontással, lineáris lépésközzel felvenni az impedancia frekvenciafüggését. Figyelem, a 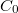párhuzamos kapacitás miatt nem egy egyszerű rezonanciagörbét látunk, hanem egy adott frekvencián antirezonancia is jelentkezik, ahol az oszcillátor árama minimális, ne feledkezzünk meg ennek a kiméréséről sem!
- A frekvenicafüggő impedanciát érdemes széles tartományban, logaritmikus skálán is felvenni. Melyik paramétert állapíthatjuk meg ebből a mérésből?
3. Egy fogó segítségével ropogtassuk meg az oszcillátor tokozásának nyakát, és távolítsuk el a tokot. Mérjük meg a kibontott oszcillátor rezonanciagörbéjét! Digitális mikroszkóp alatt kenjük be az egyik ág végét vákuumzsírral, majd helyezzünk fel az oszcillátor végére rövid rézdrót-darabokat (lásd 5. ábra). Mérjük ki, hogy a felhelyezett tömeg függvényében hogyan változik meg az oszcillátor rezonanciafrekvenciája. Az eredmények alapján határozzuk meg az oszcillátor effektív tömegét, és effektív rugóállandóját!
- Figyelem, a tömegek felhelyezésekor elromlik a hangvilla szimmetriája, és így a jósági tényező is lecsökken. Ennek megfelelően túl nagy tömeg mellett már nem tudunk jól értékelhető mérést végezni, így ügyeljünk arra, hogy vákuumzsírból a drótok felragasztásához szükséges minimális mennyiséget vigyük fel!
 |
| 5. ábra |
3. Az elektromos és mechanikai paraméterek (,, , , , 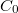) ismeretében, a fent ismertetett egyszerű modell alapján számoljuk ki, hogy 1V egyenfeszültség hatására mekkora az oszcillátor elmozdulása? Ezen eredményalapján adjunk becslést arra, hogy egy kvarc hangvillából készített atomerő mikroszkóp szenzort a rezonanciafrekvencián milyen amplitudójú a.c. feszültséggel kell gerjeszteni ahhoz, hogy a rezgési amplitudó két szomszédos atom tipikus távolságánál kisebb legyen!
Függelék: a méréshez használt eszközök
- SR830 Lock-In + használati utasítás + tápkábel
- Agilent 33220A függvénygenerátor + használati utasítás (elektronikusan) + tápkábel
- GPIB kártya USB csatlakozóval + 1 GPIB kábel
- LC kör fém dobozban
- Kvarc oszcillátor fém dobozban
- Fém doboz ellenállások befogásához termikus zaj méréséhez +
, 
, 
, 
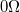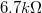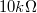-os ellenállások
- Ellenállásdekád
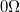-os lezáró
- Kézi multiméter
- Csavarhúzó
- 6db. közepes BNC-BNC kábel
- BNC T-elosztó
- Forrasztó páka
