„Termoelektromos jelenségek” változatai közötti eltérés
A Fizipedia wikiből
| 1. sor: | 1. sor: | ||
<wlatex> | <wlatex> | ||
| + | |||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | align="center"|[[Fájl:Termoelektromos1.jpg|közép|300px]] | ||
| + | |- | ||
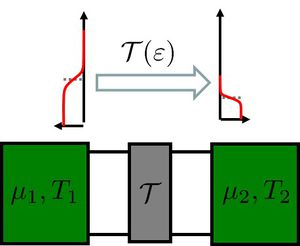
| + | | align="center"|1. ábra. ''Különböző kémiai potenciálú és hőmérsékletű elektródák közötti $\mathcal{T}$ átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték '' | ||
| + | elektromos és hőtranszport tulajdonságaira vagyunk kíváncsiak''|} | ||
| + | |||
$$I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon$$ | $$I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon$$ | ||
A lap 2018. február 22., 18:21-kori változata
1. ábra. Különböző kémiai potenciálú és hőmérsékletű elektródák közötti  átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték
elektromos és hőtranszport tulajdonságaira vagyunk kíváncsiak|} ![\[I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon\]](/images/math/2/1/2/212d11d2070e61abf720abc6d5199bd3.png) ![\[\int_{-\infty}^\infty H(\varepsilon)\cdot f(\varepsilon,\mu,T)\,\mathrm{d}\varepsilon = \int_{-\infty}^\mu H(\varepsilon)\,\mathrm{d}\varepsilon + \frac{\pi^2}{6}(kT)^2 H^\prime(\mu) + \mathrm{O} \left(\frac{kT}{\mu}\right)^4\]](/images/math/a/6/8/a689a92755262123fb0b70cfde07024e.png) ![\[I\approx\frac{2 e}{h} \cdot \int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)\,\mathrm{d}\varepsilon +\frac{2 e}{h}\frac{\pi^2}{6}(kT_1)^2 \mathcal{T}^\prime(\mu_1)-\frac{2 e}{h}\frac{\pi^2}{6}(kT_2)^2 \mathcal{T}^\prime(\mu_2)\approx \frac{2 e}{h} \cdot eV \cdot\bar{\mathcal{T}}(\varepsilon)+\frac{2 e}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot\mathcal{T}^\prime(\mu)\]](/images/math/8/8/c/88ca42f604c7170d43e54613a899873e.png) ![\[\Delta T=T_1-T_2;\ \ \ T=\frac{T_1+T_2}{2};\ \ \ \mu=\frac{\mu_1+\mu_2}{2}\]](/images/math/5/9/e/59ef26b2955577cd6210ae08aaa22a86.png) ![\[V \big|_{I=0}=\underbrace{-\frac{\pi^2 k^2 T}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon )}{\partial \varepsilon} \bigg|_{\mu}}_{S} \cdot \Delta T\]](/images/math/1/f/d/1fd92f9d3dbf2d94361fcda8c71cbd4b.png) ![\[\frac{2}{L} \sum (-e) \cdot v_k \cdot f(\varepsilon_k) = -\frac{2}{h}\int e\cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I\]](/images/math/9/6/2/962fa51a57005b7ba294d49186060e01.png)
![\[\frac{2}{L} \sum \varepsilon_k \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int \varepsilon \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_\varepsilon\]](/images/math/a/9/4/a945e6538dd014bbdef33232d9158307.png) ![\[\frac{2}{L} \sum (\varepsilon_k-\mu) \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int (\varepsilon-\mu) \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_Q\]](/images/math/1/f/7/1f7502c790238ef1d1e99aa2ab46143d.png) ![\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon\]](/images/math/2/8/8/28811e2a1ccd50c9270beb4db6f8716d.png) ![\[I_Q\approx\frac{2}{h}\frac{\pi^2}{6}(kT_1)^2\cdot\mathcal{T}(\mu) -\frac{2}{h}\frac{\pi^2}{6}(kT_2)^2\cdot \mathcal{T}(\mu) =\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot \mathcal{T}(\mu)\]](/images/math/3/3/b/33b97a30471dce6bc9afdc02a74b2a33.png) ![\[I=G\cdot V;\ \ \ I_Q=G_Q \cdot \Delta T\]](/images/math/7/3/e/73ef397ba1455b20e4f54b00b5a56ff3.png) ![\[\frac{G_Q}{G}=\mathcal{L}\cdot T;\ \ \ \mathcal{L}=\frac{\pi^2k^2}{3e^2}=2.44\times 10^{-8}\,\mathrm{W\,\Omega\,K^{-2}}\]](/images/math/f/f/3/ff3d6b12800ff710fdc4212c0c4da3ce.png) ![\[\frac{\kappa}{\sigma}=\mathcal{L}\cdot T\]](/images/math/3/b/a/3ba412299adbd9ee548fee93c769a0b5.png)
![\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T)-f_2(\varepsilon,\mu_2,T)\right]\mathrm{d}\varepsilon\]](/images/math/9/a/9/9a997fff0a9371ba14020ac2775014a1.png)
![\[I_Q\approx\frac{2}{h} \cdot \underbrace{\int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\,\mathrm{d}\varepsilon}_{\sim (eV)^2} +\frac{2}{h}\frac{\pi^2}{6}(kT)^2\left[\overbrace{\underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime |_{\mu_1}}_{\mathcal{T}(\mu_1)}- \underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime|_{\mu_2}}_{\mathcal{T}^\prime (\mu_2)(\mu_2-\mu_1)+\mathcal{T}(\mu_2)}}^{2\mathcal{T}^\prime (\mu)\cdot eV}\right]\]](/images/math/6/4/b/64bb1dc6d2eef760b79211de18692de1.png) ![\[I_Q\approx \frac{2e}{h}\frac{\pi^2 k^2 T^2}{3}\cdot \frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu \cdot V\]](/images/math/7/8/5/7857b4e85fea81f4c9f6f67dc781942f.png) ![\[I= -\frac{2e^2}{h}\mathcal{T}\cdot V\]](/images/math/a/b/a/ababe7b0669921e39c9d70cee2e50581.png) ![\[\frac{I_Q}{I}\bigg|_{T_1=T_2}\approx -\frac{\pi^2 k^2 T^2}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu =\Pi=T\cdot S\]](/images/math/0/7/d/07dab32535eec0cda541aeeb06b26c95.png)
|