„Optikai mérések” változatai közötti eltérés
(Új oldal, tartalma: „<wlatex> <!--Kategória:Mechanika--> <!--Kategória:Elektromosságtan--> <!--Kategória:Hőtan--> <!--Kategória:Kvantummechanika--> <!--Kategória:…”) |
|||
| 31. sor: | 31. sor: | ||
==Elméleti összefoglaló== | ==Elméleti összefoglaló== | ||
| − | === | + | ===Leképzés optikai lencsékkel === |
| − | + | Görbült felületek esetében a fénytörés szintén a törési törvény alapján számítható, de ekkor a beesési merőleges helyről helyre változik. | |
| − | + | {{fig3|Opt_1_kep_7.JPG|fig:8|8. ábra}} | |
| − | + | ||
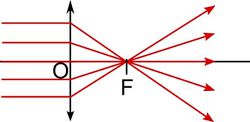
| − | + | A törési törvény alapján levezethető, hogy egy $r_1$ és $r_2$ görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha $\frac{1}{r_1}+\frac{1}{r_2}>0$. (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a [[#fig:8|8 ábrán]] láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az $f = OF$ fókusztávolság, a lencse anyagának $n$ törésmutatója és a görbületi sugarak között az | |
| − | + | $$ \frac{1}{f} = (n-1)\left(\frac{1}{r_1}+\frac{1}{r_2} \right) $$ | |
| − | + | összefüggés áll fent. | |
| − | + | {{fig3|Opt_1_kep_8.JPG|fig:9|9. ábra}} | |
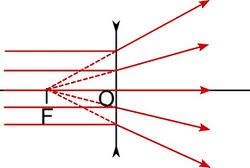
| − | $ | + | Ha $\frac{1}{r_1}+\frac{1}{r_2}<0$, akkor $f<0$, és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának ([[#fig:9|9. ábra]]). |
| − | + | {{fig3|Opt_1_kep_9.JPG|fig:10|10. ábra}} | |
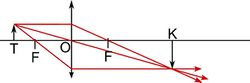
| − | $$ | + | A gyűjtőlencse egy, a fókuszpontnál távolabbi pontból kiinduló fénysugarakat egy másik pontban gyűjti össze és így létrejön a $T$ tárgy valódi (ernyőn megjeleníthető) $K$ képe (amely a nevezetes sugarak megrajzolásával könnyen megszerkeszthető, [[#fig:10|10. ábra]]). A $t=TO$ tárgytávolság, a $k=OK$ képtávolság és az $f$ fókusztávolság között az |
| − | + | $$ \frac{1}{t} + \frac{1}{k} = \frac{1}{f} $$ | |
| − | + | leképezési törvény teremt kapcsolatot. | |
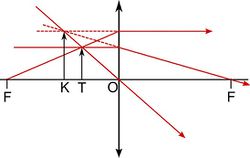
| − | + | A képlet akkor is használható, ha $f<t$ vagy ha $f$ negatív. Ekkor $k$-ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik ([[#fig:11|11. ábra]]). | |
| − | + | ||
| − | + | {{fig3|Opt_1_kep_10.JPG|fig:11|11. ábra}} | |
| − | $ | + | Több lencséből álló leképzésnél az első lencse képe a második lencse tárgya lesz. Ilyenkor, ha az első lencse által létrehozott valódi kép a második lencse mögött keletkezne, akkor $t<0$ is előfordulhat ("látszólagos tárgy"). |
| − | + | ====A mérési módszer==== | |
| − | + | =====Gyűjtőlencse fókusztávolságának mérése===== | |
| − | $$ | + | Ha a [[#fig:10|10. ábrának]] megfelelő elrendezésben egy tárgyról valódi képet hozunk létre, megmérjük a $t$ tárgytávolságot, és a $k$ képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható. |
| − | + | Ezt a nehézséget küszöböli ki a következő mérési eljárás: Állítsuk a tárgyat és az ernyőt egymástól $d$ távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha $d>4f$, akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.) | |
| + | A megfelelő tárgy- és képtávolságokat jelölje $t_1$, $k_1$ ill. $t_2$, $k_2$. A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig $s=|t_2 - t_1|$. Felhasználva, hogy a szimmetria miatt $t_2=k_1$ (és $k_2=t_1$): | ||
| − | {{ | + | $$ \frac{1}{t_1} + \frac{1}{k_1} = \frac{1}{f}, $$ |
| − | + | $$ t_1 + k_1 = d, $$ | |
| − | $$ | + | $$ |t_1 - k_1| = s. $$ |
| − | + | Az egyenletekből $t_1$-et és $k_1$-et kiküszöbölve: | |
| − | $$ \ | + | $$ f = \frac{d^2-s^2}{4d}, $$ |
| − | + | tehát a fókusztávolság $d$ és $s$ ismeretében kiszámítható. | |
| − | + | =====Szórólencse fókusztávolságának mérése===== | |
| − | + | {{fig4|Opt_1_kep_11.JPG|fig:12|12. ábra}} | |
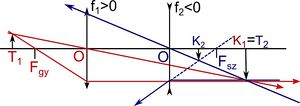
| − | + | Szórólencsével nem lehet ernyőn megjeleníthető valódi képet létrehozni, így a képtávolságot nem tudjuk mérni. Egy gyűjtő- és egy szórólencséből azonban összeállítható olyan lencserendszer, amely valódi képet ad ([[#fig:12|12. ábra]]). A $t_1=T_1O_1$, a $d=O_1O_2$ és a $k_2=O_2K_2$ távolság mérhető. | |
| − | + | Felhasználva, hogy | |
| − | + | $$ t_2 = d - k_1 < 0 $$ | |
| − | + | ||
| − | $$ | + | |
| − | + | és felírva a két lencse leképzési törvényét $f_1$, $t_1$, $d$ és $k_2$ segítségével a szórólencse fókusztávolsága kifejezhető. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| cellpadding="5" cellspacing="0" align="center" | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | {{fig2| | + | | {{fig2|Fenytores2.png|fig:13|13. ábra}} |
| − | + | ||
|- | |- | ||
|} | |} | ||
| 178. sor: | 157. sor: | ||
|} | |} | ||
| − | == | + | ==Mérési feladatok== |
| − | + | ===Leképzés optikai lencsékkel=== | |
| − | + | * '' '''Ügyeljen arra, hogy a fényforrásként használt halogén lámpa háza nagyon felforrósodhat!''' '' | |
| − | + | '''1.''' Helyezze a fényforrást és az ernyőt az optikai sín két végére! A tárgyat (diát) a fényforrás elé kb. 5 cm távolságba helyezze! Mérje meg a tárgy és az ernyő $d$ távolságát! Helyezze el az (''1'') jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti $s$ távolságot, és határozza meg a lencse fókusztávolságát! | |
| − | + | * ''Figyelem! A mérésnél használt lovasok talpa nem azonos szélességű, így a távolságokat ne a lovas talpának szélénél olvassa le!'' | |
| − | + | '''2.''' Helyezze az (''1'') jelű gyűjtőlencse és az ernyő közé a (''2'') jelű szórólencsét! Elméleti megfontolások után az ernyő és/vagy a lencsék megfelelő mozgatásával állítson elő éles képet! Mérje meg a tárgy, a lencsék és az ernyő közti távolságokat, és határozza meg a szórólencse fókusztávolságát! | |
| − | + | * ''Figyelem! Ennél a mérésnél könnyen előfordulhat olyan beállítás, melynél a távolság mérésének kicsi hibája is óriási hibát okozhat a gyújtótávolság meghatározásakor. Ezt próbálja elkerülni elméleti megfontolások segítségével, vagy a mérés megismétlésével több lényegesen eltérő lencsepozíciónál. Ugyanezen okból a gyűjtőlencse által alkotott kép pozícióját célszerű az ernyő mozgatásával közvetlenül megmérni az előző mérésben meghatározott (hibával terhelt) fókusztávolság alapján történő közvetett számolás helyett.'' | |
| − | + | '''3.''' A kis fókusztávolságú (''3'' jelű) lencse segítségével állítson össze minél nagyobb nagyítású leképzést! A tárgytartóba most az 5mm átmérőjű lyukat helyezze, melyen egy hajszál fut keresztül. A lyuk képének méretéből határozza meg a nagyítást, majd a hajszál képének szélességéből határozza meg a hajszál átmérőjét! | |
| − | + | * ''Becsülje meg a mérés hibáját!'' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
[[A méréshez rendelkezésre álló eszközök: Fénytörés és visszaverődés vizsgálata|A méréshez rendelkezésre álló eszközök]] | [[A méréshez rendelkezésre álló eszközök: Fénytörés és visszaverődés vizsgálata|A méréshez rendelkezésre álló eszközök]] | ||
| 255. sor: | 180. sor: | ||
*'' '''Figyelem! Soha ne nézzen a lézernyalábba, mert az látáskárosodást okozhat!''' '' | *'' '''Figyelem! Soha ne nézzen a lézernyalábba, mert az látáskárosodást okozhat!''' '' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Törésmutató mérése a teljes visszaverődés határszögének meghatározásával=== | ===Törésmutató mérése a teljes visszaverődés határszögének meghatározásával=== | ||
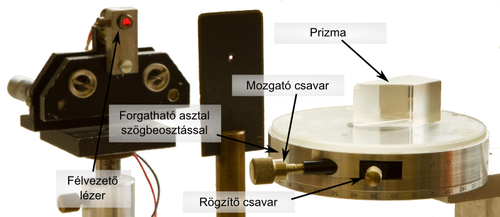
| − | ''' | + | '''4.''' Tegye fel a forgatható asztalra a prizmát! Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a prizma anyagának levegőre vonatkoztatott törésmutatóját! |
* ''A forgóasztal szögállása egy tolómérőhöz hasonló módon tizedfokos pontossággal olvasható le. A forgóasztalon egy rögzítő és egy mozgató csavar található. Finomhangoláshoz érdemes a mozgatócsavar középállásánál becsavarni a rögzítőcsavart, majd a mozgatócsavar finom állításával megkeresni a kívánt szöget. '''Figyelem! A szögérték leolvasásakor könnyen belenézhet a nyalábba, így a leolvasás előtt a lézert MINDIG KAPCSOLJA KI! A forgóasztal csavarjait ne erőltesse! Rögzített állásban kézzel ne próbálja forgatni az asztalt, ekkor csak a mozgatócsavarral lehet! ''' '' | * ''A forgóasztal szögállása egy tolómérőhöz hasonló módon tizedfokos pontossággal olvasható le. A forgóasztalon egy rögzítő és egy mozgató csavar található. Finomhangoláshoz érdemes a mozgatócsavar középállásánál becsavarni a rögzítőcsavart, majd a mozgatócsavar finom állításával megkeresni a kívánt szöget. '''Figyelem! A szögérték leolvasásakor könnyen belenézhet a nyalábba, így a leolvasás előtt a lézert MINDIG KAPCSOLJA KI! A forgóasztal csavarjait ne erőltesse! Rögzített állásban kézzel ne próbálja forgatni az asztalt, ekkor csak a mozgatócsavarral lehet! ''' '' | ||
| − | ''' | + | '''5.''' Cserélje ki a prizmát a két prizmából összeállított rendszerre! Öntsön a prizmák közé desztillált vizet. Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a víz levegőre vonatkoztatott törésmutatóját! |
* ''Az üveg tipikus törésmutatója, illetve a víz ismert törésmutatója alapján számolja ki, hogy milyen elforgatási szögeknél várja a teljes visszaverődést! (Ezt a számolást hasznos a mérési gyakorlat előtt, otthon elvégezni.) A mért értéket hasonlítsa össze a várakozással! A kétprizmás elrendezésnél legyen kifejezetten körültekintő, hiszen a teljes visszaverődéstől független geometriai okokból is megjelenhet illetve eltűnhet egy levegőbe kilépő nyaláb a forgatás közben! '' | * ''Az üveg tipikus törésmutatója, illetve a víz ismert törésmutatója alapján számolja ki, hogy milyen elforgatási szögeknél várja a teljes visszaverődést! (Ezt a számolást hasznos a mérési gyakorlat előtt, otthon elvégezni.) A mért értéket hasonlítsa össze a várakozással! A kétprizmás elrendezésnél legyen kifejezetten körültekintő, hiszen a teljes visszaverődéstől független geometriai okokból is megjelenhet illetve eltűnhet egy levegőbe kilépő nyaláb a forgatás közben! '' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</wlatex> | </wlatex> | ||
A lap 2021. szeptember 28., 22:12-kori változata
A mérés célja:
- elmélyíteni a hallgatók geometriai optikai ismereteit.
Ennek érdekében:
- áttekintjük a fénytörés és visszaverődés elméletét,
- geometriai optikai méréseket végzünk,
- vizsgáljuk a polarizált fény visszaverődését.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Leképzés optikai lencsékkel
Görbült felületek esetében a fénytörés szintén a törési törvény alapján számítható, de ekkor a beesési merőleges helyről helyre változik.
A törési törvény alapján levezethető, hogy egy 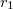 és
és 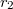 görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha
görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha 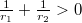 . (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a 8 ábrán láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az
. (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a 8 ábrán láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az 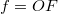 fókusztávolság, a lencse anyagának
fókusztávolság, a lencse anyagának  törésmutatója és a görbületi sugarak között az
törésmutatója és a görbületi sugarak között az
![\[ \frac{1}{f} = (n-1)\left(\frac{1}{r_1}+\frac{1}{r_2} \right) \]](/images/math/8/4/a/84a0e9228d0b072744ebe46bedec6cf1.png)
összefüggés áll fent.
Ha 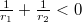 , akkor
, akkor 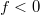 , és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának (9. ábra).
, és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának (9. ábra).
A gyűjtőlencse egy, a fókuszpontnál távolabbi pontból kiinduló fénysugarakat egy másik pontban gyűjti össze és így létrejön a  tárgy valódi (ernyőn megjeleníthető)
tárgy valódi (ernyőn megjeleníthető)  képe (amely a nevezetes sugarak megrajzolásával könnyen megszerkeszthető, 10. ábra). A
képe (amely a nevezetes sugarak megrajzolásával könnyen megszerkeszthető, 10. ábra). A 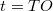 tárgytávolság, a
tárgytávolság, a 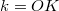 képtávolság és az
képtávolság és az  fókusztávolság között az
fókusztávolság között az
![\[ \frac{1}{t} + \frac{1}{k} = \frac{1}{f} \]](/images/math/0/e/7/0e73cce9cbf37f16a8c5467cd34538fc.png)
leképezési törvény teremt kapcsolatot.
A képlet akkor is használható, ha 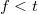 vagy ha
vagy ha  negatív. Ekkor
negatív. Ekkor  -ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik (11. ábra).
-ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik (11. ábra).
Több lencséből álló leképzésnél az első lencse képe a második lencse tárgya lesz. Ilyenkor, ha az első lencse által létrehozott valódi kép a második lencse mögött keletkezne, akkor 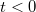 is előfordulhat ("látszólagos tárgy").
is előfordulhat ("látszólagos tárgy").
A mérési módszer
Gyűjtőlencse fókusztávolságának mérése
Ha a 10. ábrának megfelelő elrendezésben egy tárgyról valódi képet hozunk létre, megmérjük a  tárgytávolságot, és a
tárgytávolságot, és a  képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható.
képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható.
Ezt a nehézséget küszöböli ki a következő mérési eljárás: Állítsuk a tárgyat és az ernyőt egymástól  távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha
távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha 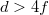 , akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.)
A megfelelő tárgy- és képtávolságokat jelölje
, akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.)
A megfelelő tárgy- és képtávolságokat jelölje 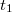 ,
, 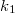 ill.
ill. 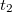 ,
, 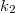 . A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig
. A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig 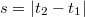 . Felhasználva, hogy a szimmetria miatt
. Felhasználva, hogy a szimmetria miatt 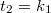 (és
(és 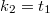 ):
):
![\[ \frac{1}{t_1} + \frac{1}{k_1} = \frac{1}{f}, \]](/images/math/4/b/9/4b9d59ca70cd713830a03cfacdb5d7a6.png)
![\[ t_1 + k_1 = d, \]](/images/math/a/7/e/a7e3335c77a51ab42b3045073e1ccd87.png)
![\[ |t_1 - k_1| = s. \]](/images/math/3/b/0/3b0499ef281b72fda0118dfe576b7c0c.png)
Az egyenletekből 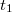 -et és
-et és 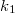 -et kiküszöbölve:
-et kiküszöbölve:
![\[ f = \frac{d^2-s^2}{4d}, \]](/images/math/0/d/f/0df5c748777c483d967c242cf30ec45d.png)
tehát a fókusztávolság  és
és  ismeretében kiszámítható.
ismeretében kiszámítható.
Szórólencse fókusztávolságának mérése
Szórólencsével nem lehet ernyőn megjeleníthető valódi képet létrehozni, így a képtávolságot nem tudjuk mérni. Egy gyűjtő- és egy szórólencséből azonban összeállítható olyan lencserendszer, amely valódi képet ad (12. ábra). A 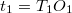 , a
, a 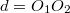 és a
és a 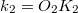 távolság mérhető.
távolság mérhető.
Felhasználva, hogy
![\[ t_2 = d - k_1 < 0 \]](/images/math/9/5/0/950b3f9ee4e4968e9e4aad051354337f.png)
és felírva a két lencse leképzési törvényét 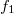 ,
, 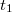 ,
,  és
és 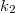 segítségével a szórólencse fókusztávolsága kifejezhető.
segítségével a szórólencse fókusztávolsága kifejezhető.
Törésmutató mérése a teljes visszaverődés határszögének meghatározásával
Két közeg sík határfelületén a fény a
![\[ \sin \alpha = n_{12}\sin \beta \]](/images/math/f/0/3/f03eb5697d3a9c19ee18f025825d8b38.png)
törési törvény szerint megtörik. Az összefüggésben  és
és  a belépő és a megtört fénysugarak beesési merőlegessel bezárt szögét,
a belépő és a megtört fénysugarak beesési merőlegessel bezárt szögét, 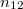 pedig a két közeg relatív törésmutatóját jelöli. A relatív törésmutató a két közeg abszolút törésmutatójának hányadosa:
pedig a két közeg relatív törésmutatóját jelöli. A relatív törésmutató a két közeg abszolút törésmutatójának hányadosa:
![\[ n_{12} = \frac{n_{2}}{n_{1}}. \]](/images/math/f/c/c/fcc73de627160897a6c60cb60a485d7d.png)
Ha a határfelületre az optikailag sűrűbb (s) közegből érkezik a fény, akkor a relatív törésmutató 1-nél kisebb. Ekkor a törési törvény alapján a fény csak akkor léphet be az optikailag ritkább (r) közegbe, ha
![\[ \alpha < \alpha_h \]](/images/math/e/a/a/eaaa8e53353bf8b8c17303905d610b89.png)
ahol 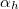 a teljes visszaverődés határszöge. A törési törvény alapján
a teljes visszaverődés határszöge. A törési törvény alapján
![\[ \sin \alpha_h = n_{sr} = \frac{1}{n_{rs}}. \]](/images/math/4/d/f/4df51c882b13ab7180cc1c838505c983.png)
Ha a beesési szög a határszögnél nagyobb, akkor a beeső fény teljesen visszaverődik. Az előző összefüggés alapján a határszög mérésével a relatív törésmutató meghatározható.
A mérési módszer
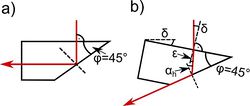
Az 7. ábrán látható, forgatható asztalra tett 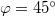 törőszögű prizmára először merőlegesen esik a lézerfény. (A merőleges beesést úgy lehet beállítani, hogy ilyenkor a részlegesen visszaverődő nyaláb éppen a lézerbe verődik vissza.) A merőlegesen belépő fénysugár törés nélkül lép be az üvegbe, majd a másik határfelületen teljesen visszaverődik, végül a prizma bal oldalán, szintén törés nélkül, kilép (5. ábra).
törőszögű prizmára először merőlegesen esik a lézerfény. (A merőleges beesést úgy lehet beállítani, hogy ilyenkor a részlegesen visszaverődő nyaláb éppen a lézerbe verődik vissza.) A merőlegesen belépő fénysugár törés nélkül lép be az üvegbe, majd a másik határfelületen teljesen visszaverődik, végül a prizma bal oldalán, szintén törés nélkül, kilép (5. ábra).
Az asztal (és a prizma) megfelelő szöggel való elforgatásával elérhető, hogy a fénysugár már nem verődik vissza teljesen, hanem 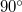 -os törési szöggel, a felületet súrolva, kilép az üvegből.
-os törési szöggel, a felületet súrolva, kilép az üvegből.
Ekkor a következő összefüggéseket írhatjuk fel:
![\[ \sin \delta = n_u \sin \varepsilon, \]](/images/math/f/d/c/fdc23f8338b8a35adf2aecdf2cacc860.png)
![\[ \alpha_h + \varepsilon = \varphi = 45^\circ, \]](/images/math/f/e/3/fe33ee236587008cee7e8dba48196d9a.png)
![\[ \sin \alpha_h = \frac{1}{n_u}. \]](/images/math/2/4/a/24a54c91407c10daf5cf29ea9d89c3fb.png)
A három összefüggés alapján 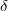 mérésével az üveg levegőre vonatkoztatott
mérésével az üveg levegőre vonatkoztatott 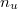 törésmutatója (valamint az
törésmutatója (valamint az  szög és az
szög és az 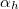 határszög) meghatározható.
határszög) meghatározható.
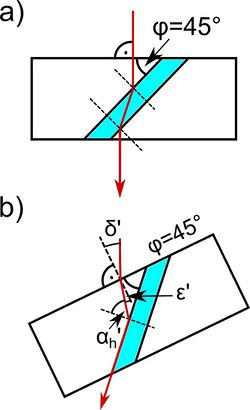
A 6 ábrán látható elrendezés két ugyanilyen prizmából van összeállítva. A két prizma közé folyadék önthető. A fénysugár most is először merőlegesen, törés nélkül lép be az üvegbe, majd megtörve belép a folyadékba, ismét megtörve átlép a másik prizmába, végül (törés nélkül) kilép a levegőbe.
Az asztal (és a prizma) megfelelő szöggel való elforgatásával ekkor is elérhető, hogy a fénysugár éppen 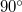 -os törési szöggel, a felületet súrolva lép ki az üvegből. A fenti összefüggések ekkor így módosulnak:
-os törési szöggel, a felületet súrolva lép ki az üvegből. A fenti összefüggések ekkor így módosulnak:
![\[ \sin \delta^\prime = n_u \sin \varepsilon^\prime, \]](/images/math/4/6/9/4697ba19810e5b150bd381d246bd966a.png)
![\[ \alpha_h^\prime - \varepsilon^\prime = \varphi = 45^\circ, \]](/images/math/4/a/6/4a69bd4bfb26d66f1fd02e74c6049ea8.png)
![\[ \sin \alpha_h^\prime = \frac{n_f}{n_u}. \]](/images/math/7/1/4/714c6c29288cfa49a93e48f812a51558.png)
Az előző mérésből 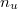 ismert, így a három összefüggés segítségével
ismert, így a három összefüggés segítségével 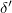 mérésével a folyadék levegőre vonatkoztatott törésmutatója (valamint az
mérésével a folyadék levegőre vonatkoztatott törésmutatója (valamint az  szög és az
szög és az 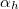 határszög) meghatározható.
határszög) meghatározható.
Mérési feladatok
Leképzés optikai lencsékkel
- Ügyeljen arra, hogy a fényforrásként használt halogén lámpa háza nagyon felforrósodhat!
1. Helyezze a fényforrást és az ernyőt az optikai sín két végére! A tárgyat (diát) a fényforrás elé kb. 5 cm távolságba helyezze! Mérje meg a tárgy és az ernyő  távolságát! Helyezze el az (1) jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti
távolságát! Helyezze el az (1) jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti  távolságot, és határozza meg a lencse fókusztávolságát!
távolságot, és határozza meg a lencse fókusztávolságát!
- Figyelem! A mérésnél használt lovasok talpa nem azonos szélességű, így a távolságokat ne a lovas talpának szélénél olvassa le!
2. Helyezze az (1) jelű gyűjtőlencse és az ernyő közé a (2) jelű szórólencsét! Elméleti megfontolások után az ernyő és/vagy a lencsék megfelelő mozgatásával állítson elő éles képet! Mérje meg a tárgy, a lencsék és az ernyő közti távolságokat, és határozza meg a szórólencse fókusztávolságát!
- Figyelem! Ennél a mérésnél könnyen előfordulhat olyan beállítás, melynél a távolság mérésének kicsi hibája is óriási hibát okozhat a gyújtótávolság meghatározásakor. Ezt próbálja elkerülni elméleti megfontolások segítségével, vagy a mérés megismétlésével több lényegesen eltérő lencsepozíciónál. Ugyanezen okból a gyűjtőlencse által alkotott kép pozícióját célszerű az ernyő mozgatásával közvetlenül megmérni az előző mérésben meghatározott (hibával terhelt) fókusztávolság alapján történő közvetett számolás helyett.
3. A kis fókusztávolságú (3 jelű) lencse segítségével állítson össze minél nagyobb nagyítású leképzést! A tárgytartóba most az 5mm átmérőjű lyukat helyezze, melyen egy hajszál fut keresztül. A lyuk képének méretéből határozza meg a nagyítást, majd a hajszál képének szélességéből határozza meg a hajszál átmérőjét!
- Becsülje meg a mérés hibáját!
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
- Figyelem! Soha ne nézzen a lézernyalábba, mert az látáskárosodást okozhat!
Törésmutató mérése a teljes visszaverődés határszögének meghatározásával
4. Tegye fel a forgatható asztalra a prizmát! Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a prizma anyagának levegőre vonatkoztatott törésmutatóját!
- A forgóasztal szögállása egy tolómérőhöz hasonló módon tizedfokos pontossággal olvasható le. A forgóasztalon egy rögzítő és egy mozgató csavar található. Finomhangoláshoz érdemes a mozgatócsavar középállásánál becsavarni a rögzítőcsavart, majd a mozgatócsavar finom állításával megkeresni a kívánt szöget. Figyelem! A szögérték leolvasásakor könnyen belenézhet a nyalábba, így a leolvasás előtt a lézert MINDIG KAPCSOLJA KI! A forgóasztal csavarjait ne erőltesse! Rögzített állásban kézzel ne próbálja forgatni az asztalt, ekkor csak a mozgatócsavarral lehet!
5. Cserélje ki a prizmát a két prizmából összeállított rendszerre! Öntsön a prizmák közé desztillált vizet. Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a víz levegőre vonatkoztatott törésmutatóját!
- Az üveg tipikus törésmutatója, illetve a víz ismert törésmutatója alapján számolja ki, hogy milyen elforgatási szögeknél várja a teljes visszaverődést! (Ezt a számolást hasznos a mérési gyakorlat előtt, otthon elvégezni.) A mért értéket hasonlítsa össze a várakozással! A kétprizmás elrendezésnél legyen kifejezetten körültekintő, hiszen a teljes visszaverődéstől független geometriai okokból is megjelenhet illetve eltűnhet egy levegőbe kilépő nyaláb a forgatás közben!