„Hőmérsékletérzékelők hitelesítése” változatai közötti eltérés
| 1. sor: | 1. sor: | ||
| − | + | <wlatex> | |
| + | __TOC__ | ||
| + | |||
| + | ''A mérés célja:'' | ||
| + | |||
| + | három elterjedten alkalmazott hőmérsékletérzékelő bemutatása: | ||
| + | |||
| + | -ellenállás-hőmérő (fém anyagú hőmérsékletfüggő ellenállás), | ||
| + | |||
| + | -termisztor (félvezető anyagú hőmérsékletfüggő ellenállás), | ||
| + | |||
| + | -termoelem. | ||
| + | |||
| + | |||
| + | ''Ennek érdekében:'' | ||
| + | |||
| + | -ismertetjük az ellenállás-hőmérő, a termisztor és a hőelem működésének alapelvét, valamint az alkalmazásukkal kapcsolatos fontosabb tudnivalókat; | ||
| + | |||
| + | -kimérjük az érzékelőket jellemző ellenállás - hőmérséklet, ill. feszültség - hőmérséklet kapcsolatokat; | ||
| + | |||
| + | -meghatározzuk az érzékelők viselkedését leíró függvények paramétereit. | ||
| + | |||
| + | |||
| + | ==Elméleti összefoglaló== | ||
| + | |||
| + | Az anyagok jellemzői általában függenek a hőmérséklettől. Elvben bármely hőmérsékletfüggő tulajdonság felhasználható hőmérő készítésére. Ennek megfelelően a hőmérsékletmérő eszközök széles skáláját fejlesztették ki. A gyakorlat során a laboratóriumokban leggyakrabban használt hőmérők kerülnek bemutatásra: az ellenállás-hőmérő, a termisztor és a termoelem. Az előbbi kettőnél az elektromos ellenállás hőmérsékletfüggését használjuk ki, míg az utóbbinál termofeszültségét. | ||
| + | |||
| + | ===Ellenállás-hőmérő ellenállásának hőmérsékletfüggése=== | ||
| + | |||
| + | [[Fájl:ellenallas_homero.JPG|bélyegkép|180px|1.ábra]] | ||
| + | |||
| + | A fémes anyagok ellenállása az | ||
| + | |||
| + | {| width = "80%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ R = R_{0} [ 1 + \alpha (T-T_{0})] \]</latex></div> | ||
| + | | align = "right" | <span id="eq1"> (1) </span> | ||
| + | |} | ||
| + | |||
| + | kifejezéssel közelíthető, ahol $ R $ és $ R_{0} $ a $ T $ ill. $ T_{0} $ hőmérsékletekhez tartozó ellenállás értékek, $ \alpha $ pedig az anyagtól függő hőmérsékleti tényező (1. ábra). $ R $, $ R_{0} $, $ T_{0} $ és $ \alpha $ ismeretében a hőmérséklet közvetlenül számítható. | ||
| + | |||
| + | ===Termisztor ellenállásának hőmérsékletfüggése=== | ||
| + | |||
| + | [[Fájl:Felvezeto_homero.jpg|bélyegkép|180px|2.ábra]] | ||
| + | |||
| + | A félvezető anyagok ellenállása jól közelíthető az | ||
| + | |||
| + | {| width = "80%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ R = A e^\frac{B}{T} \]</latex></div> | ||
| + | | align = "right" | <span id="eq2"> (2) </span> | ||
| + | |} | ||
| + | |||
| + | kifejezéssel (2. ábra), ahol $ A $ a $ T = \infty $ értékhez tartozó ún. maradékellenállás, és $ B > 0 $ a félvezető anyagára jellemző állandó ($ B = \Delta E / k $, ahol $ \Delta E $ a félvezető tiltott sáv szélessége, $ k $ pedig a Boltzmann-állandó). | ||
| + | |||
| + | A (2) kifejezés természetes alapú logaritmusát véve | ||
| + | |||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ \textrm{ln} R = \textrm{ln} A + \frac{B}{T}. \]</latex></div> | ||
| + | | align = "right" | <span id="eq3"> (3) </span> | ||
| + | |} | ||
| + | |||
| + | Ha tehát a mért ellenállás értékek logaritmusát $ 1/T $ függvényében ábrázoljuk egyenest kapunk (2. a) és 2. b) ábra), melynek tengelymetszetéből ill. meredekségéből $ A $ és $ B $ meghatározható. | ||
| + | |||
| + | ===Ellenállás-hőmérők és termisztorok összehasonlítása=== | ||
| + | |||
| + | Az ellenállás-hőmérő és a termisztor ellenállása függ a hőmérséklettől. Az előbbi esetben az elektronok mozgékonyságának csökkenése miatt az ellenállás növekszik a hőmérséklettel. Ezzel szemben a termisztor ellenállása csökken, mivel a hőmérséklet emelkedésével nő a töltéshordozók koncentrációja. A két érzékelő jellemzőit az 1. táblázatban hasonlítjuk össze. | ||
| + | |||
| + | {| border="1" | ||
| + | |+ 1. Táblázat | ||
| + | ! scope="col" | Tulajdonság | ||
| + | ! scope="col" | Ellenállás-hőmérő | ||
| + | ! scope="col" | Termisztor | ||
| + | |- | ||
| + | ! scope="row" | Hőfoktényező | ||
| + | | kicsi, $ ~10^{-3} \textrm{K}^{-1} $ || nagy, $ T $-függő | ||
| + | |- | ||
| + | ! scope="row" | $ R $ $(20 $ $^\circ C)$ | ||
| + | | $ ~ 100 $ $\Omega $ || k$ \Omega $ nagyságrendű | ||
| + | |- | ||
| + | ! scope="row" | Stabilitás | ||
| + | | jó || gyengébb | ||
| + | |- | ||
| + | ! scope="row" | Reprodukálhatóság | ||
| + | | jó || gyengébb | ||
| + | |- | ||
| + | ! scope="row" | Karakterisztika | ||
| + | | lineáris || exponenciális | ||
| + | |- | ||
| + | ! scope="row" | Tömeg | ||
| + | | > termisztor || < ellenállás-hőmérő | ||
| + | |- | ||
| + | ! scope="row" | Hőtehetetlenség | ||
| + | | > termisztor || < ellenállás-hőmérő | ||
| + | |- | ||
| + | ! scope="row" | Ár | ||
| + | | > termisztor || < ellenállás-hőmérő | ||
| + | |- | ||
| + | ! scope="row" | Hőmérséklet tartomány | ||
| + | | -183-tól 630 $^\circ C$-ig || -60-tól 150 $^\circ C$-ig | ||
| + | |- | ||
| + | ! scope="row" | Anyaga | ||
| + | | Pt, Cu, Ni, ötvözetek || különféle félvezetők | ||
| + | |} | ||
| + | |||
| + | ===A hőelem (termoelem)=== | ||
| + | |||
| + | Két különböző fém érintkezésekor a két fém között elektromos feszültség mérhető. Ez a feszültség az ún. kontaktpotenciál, melynek nagysága az érintkező fémek anyagi minőségétől és az érintkezési pont hőmérsékletétől függ. | ||
| + | |||
| + | [[Fájl:Termoelem.jpg|bélyegkép|180px|3.ábra]] | ||
| + | |||
| + | Ha a 3. ábrán látható kapcsolást három különböző [(1)-es, (2)-es, és (3)-as jelzésű] fémből alakítjuk ki, de minden pont azonos hőmérsékleten van, akkor a D és az E pontok között nem jelentkezik feszültség. | ||
| + | Amennyiben valamelyik fém-fém átmenet (A, B vagy C pontok) hőmérséklete megváltozik, akkor D és E között feszültség mérhető, melynek értéke arányos a hőmérséklet változással. Tehát, ha az A átmenet hőmérsékletét kívánjuk mérni, akkor a másik két átmenet (B és C pont) hőmérsékletét állandó értéken – a hitelesítés hőmérsékletén – kell tartani, ekkor D és E között az A pont hőmérsékletének megváltozásával arányos feszültség mérhető. A többi pont hőmérsékletének állandó értéken tartása azért fontos, mert ellenkező esetben a fellépő kontaktpotenciál változások meghamisíthatják a mérést. Ezen nehézségeket a két összekapcsolt termoelemből álló ún. termopár (4. ábra) segítségével küszöbölhetjük ki. | ||
| + | |||
| + | [[Fájl:Termopar.jpg|bélyegkép|180px|4.ábra]] | ||
| + | |||
| + | A termopárt alkotó kontaktusok (B és C) az (1) és (2) anyagokat kötik össze, míg a (3) anyagból készült elvezető huzalok az A és a D pontokon kapcsolódnak a termopárhoz. | ||
| + | Először a termopáron kialakuló feszültséggel - vagyis az A’ és D’ pontok között fellépő feszültséggel foglalkozunk [A’ és D’ az (1) anyagban, az A és D pontok közelében levő két pont]. Ha B és C hőmérséklete különböző, vagyis $ t_{x} = t_{0} + \Delta t $, akkor az A’ és D’ pontok között megjelenő feszültség arányos hőmérsékletkülönbséggel. | ||
| + | |||
| + | {| width = "80%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ \begin{array}{rcl} U_{A^\prime B^\prime} &=& U_{12}(t_{0}+\Delta t)-U_{12}(t_{0}) \\ U_{A^\prime B^\prime} &=& \alpha_{12}\Delta t \end{array}\]</latex></div> | ||
| + | | align = "right" | <span id="eq4> (4) </span> | ||
| + | |} | ||
| + | |||
| + | ahol az indexben levő számok a termoelemet alkotó anyagokra utalnak, és kihasználtuk, hogy a szembe kapcsolt termoelemekre $ U_{21}(t) = -U_{12}(t) $. A lineáris közelítés szűk hőmérséklet-tartományban illetve kisebb pontossági igények esetén alkalmazható. Szélesebb hőmérsékleti intervallumban további állandók bevezetése szükséges: | ||
| + | |||
| + | |||
| + | {| width = "100%" | ||
| + | |- | ||
| + | | width = "10%" | | ||
| + | | width = "80%" | <div class="texdisplay"><latex display >\[ U_{A^\prime B^\prime} = \alpha_{12}\Delta t + \beta_{12}\Delta t^2 + ... \]</latex></div> | ||
| + | | align = "right" | <span id="eq5> (5) </span> | ||
| + | |} | ||
| + | |||
| + | A (4) összefüggés szerint a termopár kimenetén a B és C pontok közti hőmérsékletkülönbséggel arányos feszültség jelenik meg. Ha tehát hőmérőként kívánjuk használni, akkor az egyik átmenetet ismert hőmérsékleten kell tartani. A vonatkoztatási hőmérséklet általában 0 $^\circ C$, ami olvadó jég segítségével könnyen előállítható és tartható. (A pontosság növelése érdekében célszerű desztillált vízből készíteni a jeget.) | ||
| + | Ennél a kapcsolásnál tehát a hőmérsékletmérés a B és a C pontoknál levő átmenetek segítségével történik. A mérőműszernél (E és F pontok), valamint az elvezető huzalok csatlakozási pontjainál (A és D) azonban elkerülhetetlenül további “járulékos” termoelemek alakulnak ki. Ezek – az A’ és D’ pontoktól a kijelzőig terjedő – ”járulékos” termoelemek páronként azonos anyagból állnak. [Például az A és a D pontokon az (1)-es és a (3) jelű anyagból.] Így a keletkezett termofeszültségek szembekapcsolódnak. Mérés közben tehát csak arra kell ügyelni hogy ezen átmeneteknek páronként (A-nak D-vel és E-nek F-el) azonos legyen a hőmérséklete. Ez a feltétel aránylag könnyen teljesíthető az átmenetek közötti jó termikus kapcsolattal. Pontos mérésnél figyelembe kell venni a termopár és a vezetékek ellenállásán eső feszültséget is. A feszültség kompenzációs módszerrel történő mérésénél ez a probléma elkerülhető. | ||
| + | |||
| + | ==Hitelesítés== | ||
| + | |||
| + | A hitelesítés jelen esetben az érzékelők hőmérséklet - ellenállás ill. hőmérséklet – termofeszültség függvényeinek meghatározását jelenti. A mérésnél a hőmérséklet-érzékelőket olajjal töltött dupla falú üvegedénybe (hőcserélőbe) helyezzük egy-egy “hiteles” higanyos hőmérővel együtt (termopár esetében csak az egyik termoelem kerül olajfürdőbe, a másik víz-jég keverékbe merül). Az olajfürdő hőmérsékletét az üvegedény falában áramoltatott, termosztáttal szabályozott hőmérsékletű víz segítségével állítjuk be. A különböző eszközök hőtehetetlensége miatt fellépő hiba kiküszöbölése érdekében, állandósult hőmérsékleten (stacioner állapotban) végezzük a méréseket! | ||
| + | Az olajfürdő hőmérsékletét és a megfelelő ellenállás ill. feszültség értékeket 5 $^\circ C$-ként olvassuk le! A méréseket a hőmérsékleti egyensúly beállta után végezzük, amit az ellenállás ill. feszültség időbeli állandósága jelez. | ||
| + | Az ellenállásokat lehet [http://hu.wikipedia.org/wiki/Wheatstone-h%C3%ADd Wheatstone-híd]dal, a feszültségeket pedig kompenzációs módszerrel is mérni. A mérési gyakorlaton a méréseket digitális multiméterrel végezze! | ||
| + | |||
| + | ==Mérési feladatok== | ||
| + | |||
| + | 1. Állapítsa meg az ellenállás-hőmérő és a termisztor ellenállásának, valamint a hőelem termofeszültségének hőmérsékletfüggését a hőmérséklet növekedése közben! A méréseket multiméterrel végezze! A hőmérsékletet a szobahőmérséklettől kb. 60 $^\circ C$-ig változtassa! | ||
| + | |||
| + | 2. Végezze el a feladatot csökkenő hőmérséklet mellett is! | ||
| + | |||
| + | 3. Mérési eredményeit ábrázolja diagramon! | ||
| + | |||
| + | 4. Az ellenállás-hőmérő és a termoelem vizsgálata során kapott mérési pontokra illesszen egyenest! Határozza meg az érzékelők paramétereit és adja meg hibájukat! | ||
| + | |||
| + | 5. A termisztoron végzett mérés eredményeit ábrázolja $ \textrm{ln} R $ – $ \frac{1}{T} $ formában! A kapott pontokra illesszen egyenest, határozza meg a termisztor A és B paramétereit és adja meg a hibájukat! | ||
| + | |||
| + | 6. Mérje meg a hőelem belső ellenállását! | ||
| + | A termoelem és a félvezető termoelem belső ellenállásához mérni kell | ||
| + | |||
| + | a) a termoelem üresjárati feszültségét ($ U_0 $) | ||
| + | |||
| + | b) a termoelem áramát egy ismert ellenálláson keresztül ($I$). | ||
| + | |||
| + | Ez az ismert ellenállás maga az árammérő is lehet, pl. 200 mA méréshatáron. Az árammérő ellenállását ($ R_A $, ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. (Az ellenállásmérőt egyszerűen rákötjük a – természetesen más áramkörbe ezalatt be nem kötött –, megfelelő méréshatárra beállított árammérőre.) | ||
| + | Ezután a termoelem $ R_b $ belső ellenállása a Kirchhoff-törvények alapján számolható. | ||
| + | Vegye figyelembe a huzalok ellenállását is! | ||
A lap 2012. február 10., 10:39-kori változata
Tartalomjegyzék[elrejtés] |
A mérés célja:
három elterjedten alkalmazott hőmérsékletérzékelő bemutatása:
-ellenállás-hőmérő (fém anyagú hőmérsékletfüggő ellenállás),
-termisztor (félvezető anyagú hőmérsékletfüggő ellenállás),
-termoelem.
Ennek érdekében:
-ismertetjük az ellenállás-hőmérő, a termisztor és a hőelem működésének alapelvét, valamint az alkalmazásukkal kapcsolatos fontosabb tudnivalókat;
-kimérjük az érzékelőket jellemző ellenállás - hőmérséklet, ill. feszültség - hőmérséklet kapcsolatokat;
-meghatározzuk az érzékelők viselkedését leíró függvények paramétereit.
Elméleti összefoglaló
Az anyagok jellemzői általában függenek a hőmérséklettől. Elvben bármely hőmérsékletfüggő tulajdonság felhasználható hőmérő készítésére. Ennek megfelelően a hőmérsékletmérő eszközök széles skáláját fejlesztették ki. A gyakorlat során a laboratóriumokban leggyakrabban használt hőmérők kerülnek bemutatásra: az ellenállás-hőmérő, a termisztor és a termoelem. Az előbbi kettőnél az elektromos ellenállás hőmérsékletfüggését használjuk ki, míg az utóbbinál termofeszültségét.
Ellenállás-hőmérő ellenállásának hőmérsékletfüggése
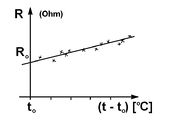
A fémes anyagok ellenállása az
![\[ R = R_{0} [ 1 + \alpha (T-T_{0})] \]](/images/math/7/4/7/74703d7c3b5acd48660572be40b12e97.png) |
(1) |
kifejezéssel közelíthető, ahol 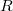 és
és 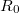 a
a 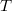 ill.
ill. 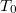 hőmérsékletekhez tartozó ellenállás értékek,
hőmérsékletekhez tartozó ellenállás értékek, 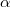 pedig az anyagtól függő hőmérsékleti tényező (1. ábra).
pedig az anyagtól függő hőmérsékleti tényező (1. ábra). 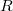 ,
, 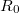 ,
, 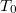 és
és 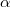 ismeretében a hőmérséklet közvetlenül számítható.
ismeretében a hőmérséklet közvetlenül számítható.
Termisztor ellenállásának hőmérsékletfüggése
A félvezető anyagok ellenállása jól közelíthető az
![\[ R = A e^\frac{B}{T} \]](/images/math/b/3/b/b3b985be0ac8c214b1a7d3692a827fac.png) |
(2) |
kifejezéssel (2. ábra), ahol 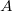 a
a 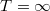 értékhez tartozó ún. maradékellenállás, és
értékhez tartozó ún. maradékellenállás, és 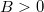 a félvezető anyagára jellemző állandó (
a félvezető anyagára jellemző állandó (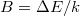 , ahol
, ahol 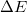 a félvezető tiltott sáv szélessége,
a félvezető tiltott sáv szélessége, 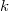 pedig a Boltzmann-állandó).
pedig a Boltzmann-állandó).
A (2) kifejezés természetes alapú logaritmusát véve
![\[ \textrm{ln} R = \textrm{ln} A + \frac{B}{T}. \]](/images/math/1/a/b/1ab4679644351138d950b3b7bbd0a5d7.png) |
(3) |
Ha tehát a mért ellenállás értékek logaritmusát 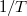 függvényében ábrázoljuk egyenest kapunk (2. a) és 2. b) ábra), melynek tengelymetszetéből ill. meredekségéből
függvényében ábrázoljuk egyenest kapunk (2. a) és 2. b) ábra), melynek tengelymetszetéből ill. meredekségéből 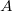 és
és 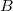 meghatározható.
meghatározható.
Ellenállás-hőmérők és termisztorok összehasonlítása
Az ellenállás-hőmérő és a termisztor ellenállása függ a hőmérséklettől. Az előbbi esetben az elektronok mozgékonyságának csökkenése miatt az ellenállás növekszik a hőmérséklettel. Ezzel szemben a termisztor ellenállása csökken, mivel a hőmérséklet emelkedésével nő a töltéshordozók koncentrációja. A két érzékelő jellemzőit az 1. táblázatban hasonlítjuk össze.
| Tulajdonság | Ellenállás-hőmérő | Termisztor |
|---|---|---|
| Hőfoktényező | kicsi, 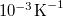 |
nagy, 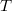 -függő -függő
|
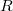 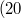 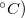
|
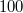 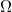 |
k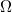 nagyságrendű nagyságrendű
|
| Stabilitás | jó | gyengébb |
| Reprodukálhatóság | jó | gyengébb |
| Karakterisztika | lineáris | exponenciális |
| Tömeg | > termisztor | < ellenállás-hőmérő |
| Hőtehetetlenség | > termisztor | < ellenállás-hőmérő |
| Ár | > termisztor | < ellenállás-hőmérő |
| Hőmérséklet tartomány | -183-tól 630 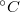 -ig -ig |
-60-tól 150 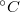 -ig -ig
|
| Anyaga | Pt, Cu, Ni, ötvözetek | különféle félvezetők |
A hőelem (termoelem)
Két különböző fém érintkezésekor a két fém között elektromos feszültség mérhető. Ez a feszültség az ún. kontaktpotenciál, melynek nagysága az érintkező fémek anyagi minőségétől és az érintkezési pont hőmérsékletétől függ.
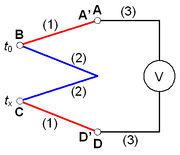
Ha a 3. ábrán látható kapcsolást három különböző [(1)-es, (2)-es, és (3)-as jelzésű] fémből alakítjuk ki, de minden pont azonos hőmérsékleten van, akkor a D és az E pontok között nem jelentkezik feszültség. Amennyiben valamelyik fém-fém átmenet (A, B vagy C pontok) hőmérséklete megváltozik, akkor D és E között feszültség mérhető, melynek értéke arányos a hőmérséklet változással. Tehát, ha az A átmenet hőmérsékletét kívánjuk mérni, akkor a másik két átmenet (B és C pont) hőmérsékletét állandó értéken – a hitelesítés hőmérsékletén – kell tartani, ekkor D és E között az A pont hőmérsékletének megváltozásával arányos feszültség mérhető. A többi pont hőmérsékletének állandó értéken tartása azért fontos, mert ellenkező esetben a fellépő kontaktpotenciál változások meghamisíthatják a mérést. Ezen nehézségeket a két összekapcsolt termoelemből álló ún. termopár (4. ábra) segítségével küszöbölhetjük ki.
A termopárt alkotó kontaktusok (B és C) az (1) és (2) anyagokat kötik össze, míg a (3) anyagból készült elvezető huzalok az A és a D pontokon kapcsolódnak a termopárhoz.
Először a termopáron kialakuló feszültséggel - vagyis az A’ és D’ pontok között fellépő feszültséggel foglalkozunk [A’ és D’ az (1) anyagban, az A és D pontok közelében levő két pont]. Ha B és C hőmérséklete különböző, vagyis 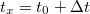 , akkor az A’ és D’ pontok között megjelenő feszültség arányos hőmérsékletkülönbséggel.
, akkor az A’ és D’ pontok között megjelenő feszültség arányos hőmérsékletkülönbséggel.
![\[ \begin{array}{rcl} U_{A^\prime B^\prime} &=& U_{12}(t_{0}+\Delta t)-U_{12}(t_{0}) \\ U_{A^\prime B^\prime} &=& \alpha_{12}\Delta t \end{array}\]](/images/math/3/9/b/39b4b3571e8c6d87f1076f277ea48866.png) |
(4) |
ahol az indexben levő számok a termoelemet alkotó anyagokra utalnak, és kihasználtuk, hogy a szembe kapcsolt termoelemekre 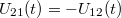 . A lineáris közelítés szűk hőmérséklet-tartományban illetve kisebb pontossági igények esetén alkalmazható. Szélesebb hőmérsékleti intervallumban további állandók bevezetése szükséges:
. A lineáris közelítés szűk hőmérséklet-tartományban illetve kisebb pontossági igények esetén alkalmazható. Szélesebb hőmérsékleti intervallumban további állandók bevezetése szükséges:
![\[ U_{A^\prime B^\prime} = \alpha_{12}\Delta t + \beta_{12}\Delta t^2 + ... \]](/images/math/8/b/c/8bc30b23a93bef80778c8bdcb53c7b26.png) |
(5) |
A (4) összefüggés szerint a termopár kimenetén a B és C pontok közti hőmérsékletkülönbséggel arányos feszültség jelenik meg. Ha tehát hőmérőként kívánjuk használni, akkor az egyik átmenetet ismert hőmérsékleten kell tartani. A vonatkoztatási hőmérséklet általában 0 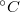 , ami olvadó jég segítségével könnyen előállítható és tartható. (A pontosság növelése érdekében célszerű desztillált vízből készíteni a jeget.)
Ennél a kapcsolásnál tehát a hőmérsékletmérés a B és a C pontoknál levő átmenetek segítségével történik. A mérőműszernél (E és F pontok), valamint az elvezető huzalok csatlakozási pontjainál (A és D) azonban elkerülhetetlenül további “járulékos” termoelemek alakulnak ki. Ezek – az A’ és D’ pontoktól a kijelzőig terjedő – ”járulékos” termoelemek páronként azonos anyagból állnak. [Például az A és a D pontokon az (1)-es és a (3) jelű anyagból.] Így a keletkezett termofeszültségek szembekapcsolódnak. Mérés közben tehát csak arra kell ügyelni hogy ezen átmeneteknek páronként (A-nak D-vel és E-nek F-el) azonos legyen a hőmérséklete. Ez a feltétel aránylag könnyen teljesíthető az átmenetek közötti jó termikus kapcsolattal. Pontos mérésnél figyelembe kell venni a termopár és a vezetékek ellenállásán eső feszültséget is. A feszültség kompenzációs módszerrel történő mérésénél ez a probléma elkerülhető.
, ami olvadó jég segítségével könnyen előállítható és tartható. (A pontosság növelése érdekében célszerű desztillált vízből készíteni a jeget.)
Ennél a kapcsolásnál tehát a hőmérsékletmérés a B és a C pontoknál levő átmenetek segítségével történik. A mérőműszernél (E és F pontok), valamint az elvezető huzalok csatlakozási pontjainál (A és D) azonban elkerülhetetlenül további “járulékos” termoelemek alakulnak ki. Ezek – az A’ és D’ pontoktól a kijelzőig terjedő – ”járulékos” termoelemek páronként azonos anyagból állnak. [Például az A és a D pontokon az (1)-es és a (3) jelű anyagból.] Így a keletkezett termofeszültségek szembekapcsolódnak. Mérés közben tehát csak arra kell ügyelni hogy ezen átmeneteknek páronként (A-nak D-vel és E-nek F-el) azonos legyen a hőmérséklete. Ez a feltétel aránylag könnyen teljesíthető az átmenetek közötti jó termikus kapcsolattal. Pontos mérésnél figyelembe kell venni a termopár és a vezetékek ellenállásán eső feszültséget is. A feszültség kompenzációs módszerrel történő mérésénél ez a probléma elkerülhető.
Hitelesítés
A hitelesítés jelen esetben az érzékelők hőmérséklet - ellenállás ill. hőmérséklet – termofeszültség függvényeinek meghatározását jelenti. A mérésnél a hőmérséklet-érzékelőket olajjal töltött dupla falú üvegedénybe (hőcserélőbe) helyezzük egy-egy “hiteles” higanyos hőmérővel együtt (termopár esetében csak az egyik termoelem kerül olajfürdőbe, a másik víz-jég keverékbe merül). Az olajfürdő hőmérsékletét az üvegedény falában áramoltatott, termosztáttal szabályozott hőmérsékletű víz segítségével állítjuk be. A különböző eszközök hőtehetetlensége miatt fellépő hiba kiküszöbölése érdekében, állandósult hőmérsékleten (stacioner állapotban) végezzük a méréseket!
Az olajfürdő hőmérsékletét és a megfelelő ellenállás ill. feszültség értékeket 5 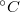 -ként olvassuk le! A méréseket a hőmérsékleti egyensúly beállta után végezzük, amit az ellenállás ill. feszültség időbeli állandósága jelez.
Az ellenállásokat lehet Wheatstone-híddal, a feszültségeket pedig kompenzációs módszerrel is mérni. A mérési gyakorlaton a méréseket digitális multiméterrel végezze!
-ként olvassuk le! A méréseket a hőmérsékleti egyensúly beállta után végezzük, amit az ellenállás ill. feszültség időbeli állandósága jelez.
Az ellenállásokat lehet Wheatstone-híddal, a feszültségeket pedig kompenzációs módszerrel is mérni. A mérési gyakorlaton a méréseket digitális multiméterrel végezze!
Mérési feladatok
1. Állapítsa meg az ellenállás-hőmérő és a termisztor ellenállásának, valamint a hőelem termofeszültségének hőmérsékletfüggését a hőmérséklet növekedése közben! A méréseket multiméterrel végezze! A hőmérsékletet a szobahőmérséklettől kb. 60 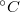 -ig változtassa!
-ig változtassa!
2. Végezze el a feladatot csökkenő hőmérséklet mellett is!
3. Mérési eredményeit ábrázolja diagramon!
4. Az ellenállás-hőmérő és a termoelem vizsgálata során kapott mérési pontokra illesszen egyenest! Határozza meg az érzékelők paramétereit és adja meg hibájukat!
5. A termisztoron végzett mérés eredményeit ábrázolja 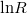 –
– 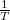 formában! A kapott pontokra illesszen egyenest, határozza meg a termisztor A és B paramétereit és adja meg a hibájukat!
formában! A kapott pontokra illesszen egyenest, határozza meg a termisztor A és B paramétereit és adja meg a hibájukat!
6. Mérje meg a hőelem belső ellenállását! A termoelem és a félvezető termoelem belső ellenállásához mérni kell
a) a termoelem üresjárati feszültségét (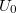 )
)
b) a termoelem áramát egy ismert ellenálláson keresztül ( ).
).
Ez az ismert ellenállás maga az árammérő is lehet, pl. 200 mA méréshatáron. Az árammérő ellenállását (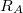 , ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. (Az ellenállásmérőt egyszerűen rákötjük a – természetesen más áramkörbe ezalatt be nem kötött –, megfelelő méréshatárra beállított árammérőre.)
Ezután a termoelem
, ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. (Az ellenállásmérőt egyszerűen rákötjük a – természetesen más áramkörbe ezalatt be nem kötött –, megfelelő méréshatárra beállított árammérőre.)
Ezután a termoelem 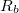 belső ellenállása a Kirchhoff-törvények alapján számolható.
Vegye figyelembe a huzalok ellenállását is!
belső ellenállása a Kirchhoff-törvények alapján számolható.
Vegye figyelembe a huzalok ellenállását is!