„Mozgás és megjelenítése” változatai közötti eltérés
(Új oldal, tartalma: „<wlatex> Történelmünk során a helymeghatározás (navigáció) mindvégig a sikeres kereskedés és a felfedezések egyik fontos kelléke volt. A fejlődést jól pél…”) |
|||
| 1. sor: | 1. sor: | ||
<wlatex> | <wlatex> | ||
| − | + | Minden mozog körülöttünk. Vajon mi lehet a mozgások oka, milyen természettörvények írják le a mozgásokat? „Már a régi görögök is” sokat gondolkoztak ezen, mégis mintegy 2000 évnek kellett eltelnie, mire – Newton munkásságának köszönhetően – pontos választ kaphattunk ezekre a kérdésekre. Newton törvényeinek ismerete elengedhetetlen a környező világ mozgásainak megértéséhez a bolygómozgásoktól kezdve a biliárdgolyókon keresztül egészen az atomi felbontású alagútmikroszkóp piezo mozgatójáig. A mozgásegyenletek megoldásában sokat segíthet a számítógép. Ugyanakkor a számítógépes animációk is csak akkor élethűek, ha tükrözik ezeket a szabályszerűségeket. | |
__TOC__ | __TOC__ | ||
| − | == | + | ==Az erő== |
| − | === | + | ===Deformáció és mozgásállapot-változás=== |
| − | + | A hétköznapi tapasztalat alapján könnyen arra a téves megállapításra juthatunk, amit az ókori gondolkodók is vallottak, hogy egy test mozgásának a fenntartásához külső hatás szükséges: ahhoz, hogy vízszintes talajon egyenletes sebességgel biciklizzünk, folyamatosan tekerni kell, különben a bicikli előbb-utóbb megáll. A jelenség részletesebb vizsgálatával azonban rájöhetünk, hogy a biciklire rajtunk kívül más is hat (például a légellenállás vagy a gördülési ellenállás) és nekünk éppen azért kell tekernünk, hogy ezeket a hatásokat kiegyenlítsük. Ha egy testet minden más test hatásától mentesen (például a világűrben, az égitestektől távol) magára hagyunk, akkor a kezdeti sebességét megtartva egyenes vonalú egyenletes mozgással fog mozogni. | |
| − | + | ||
| − | A | + | A [http://en.wikipedia.org/wiki/Isaac_Newton newtoni] dinamika alapvető állítása, hogy nem a mozgás fenntartásához, hanem a mozgásállapot megváltoztatásához van szükség külső hatásra. Ez a külső hatás az [http://en.wikipedia.org/wiki/Force erő]. A testet érő hatásnak a nagysága és az iránya is fontos: az erő vektoriális mennyiség. |
| − | + | A testre ható erő azonban nem csak a test mozgásállapotát változtatja meg, hanem a testet kisebb-nagyobb mértékben deformálja is. A test alakváltozása (deformációja) lehetőséget ad az erő egyszerű mérésére. | |
| − | === | + | ===Erőmérés=== |
| − | + | A testre ható erő és a test deformációja között általában nagyon bonyolult a kapcsolat. Az erő méréséhez leginkább rugalmas testek aránylag kismértékű alakváltozása alkalmas. Rugalmas testet azért célszerű választani, mert az az erőhatás megszűntével újra felveszi eredeti alakját. Ezen kívül legtöbb rugalmas test deformációja a tapasztalat szerint aránylag kis alakváltozás esetén lineárisan változik az erőhatással. | |
| − | + | Ilyen erőmérő eszköz az egyszerű rúgós erőmérő is, de a mérni kívánt erő nagyságától, a mérés pontosságától függően sokféle ilyen elven működő eszköz készíthető. | |
| − | + | ===Newton III. törvénye=== | |
| + | Az erő mindig két test közötti kölcsönhatás. Ha egy A test hat egy másik, B testre, akkor a B test is hatni fog az A testre. A tapasztalat szerint a két erő azonos nagyságú, de ellentétes irányú. Ezt a tapasztalatot fogalmazza meg Newton III. törvénye (hatás-ellenhatás törvénye): $$\vec{F}_{\rm AB}=-\vec{F}_{\rm BA}$$ | ||
| + | [[#Tehetetlenségi erő| Később]] (a jelenségek egyszerűbb leírása érdekében) be fogunk vezetni fiktív (nem valóságos) erőket, melyek nem kölcsönhatások. Egy testre ható valódi erő esetében azonban mindig meg lehet találni azt a másik testet, amely hat rá. | ||
| − | + | ==Newton II. törvénye== | |
| + | ===A tehetetlen tömeg=== | ||
| + | Egy test a rá ható erő hatására megváltoztatja mozgásállapotát, azaz meg fog változni a sebessége (a sebesség nagysága, iránya vagy nagysága és iránya). A tapasztalat szerint a test gyorsulása arányos a testre ható erő nagyságával: $$a \sim F\qquad{\rm vagy}\qquad\frac{F}{a}={\rm const.}$$ | ||
| + | Az arányossági tényező a testre jellemző állandó. Minél nagyobb ez az állandó, annál kevésbé változtatja meg a mozgásállapotát egy adott erő hatására a test, annál nehezebb elindítani (vagy megállítani), annál „tehetetlenebb”. A testre ható erő és a hatására létrejövő gyorsulás hányadosa a test tehetetlen [http://en.wikipedia.org/wiki/Mass tömege]. $$\frac{F}{a}=m$$ | ||
| + | A tapasztalat szerint a gyorsulás iránya megegyezik az erő irányával. Ezt is figyelembe véve felírható a testre ható erő, a test tömege és gyorsulás közötti kapcsolat. Ez Newton II. törvénye (a dinamika alapegyenlete): $$\vec{F}=m\vec{a}$$ | ||
| + | Egy testre általában nem csak egy erő hat. A testre ható $\vec{F}_1, \vec{F}_2, \dots$ erők külön-külön $\vec{a}_1, \vec{a}_2, \dots$ gyorsulásokat okoznának. Ha az erők egyszerre hatnak a testre, akkor a test gyorsulása ezeknek a gyorsulásoknak az összege lesz, tehát az erők egymástól függetlenül hatnak (erőhatások függetlenségének elve, szokás Newton IV. törvényének is nevezni): $$\vec{a}=\vec{a}_1+\vec{a}_2+\dots=\frac{\vec{F}_1}{m}+\frac{\vec{F}_2}{m}+\dots=\frac{\Sigma\vec{F}}{m}$$ | ||
| − | A | + | ===A tömeg és az erő mértékegysége=== |
| + | A tömeg SI mértékegysége a [http://en.wikipedia.org/wiki/Kilogram kilogramm] (kg). Ezt a mértékegységet még nem vezették vissza alapvető természeti állandókra. Eredeti meghatározása szerint 1 dm<math>^3</math> 4°C-os víz tömege, 1889 óta pedig 1 kg a kilogramm etalon (egy Párizs közelében őrzött platina-irídium henger) tömege. A mértékegység másik zavaró furcsasága, hogy az SI alapegység történeti okokból kilo- [http://en.wikipedia.org/wiki/SI_prefix előtagot] tartalmaz. | ||
| − | + | Az erő SI mértékegysége a [http://en.wikipedia.org/wiki/Newton_(unit) newton] (N). 1 N az az erő, ami egy 1 kg tömegű testet 1 m/s<math>^2</math> gyorsulással gyorsít. Az erő régebbi mértékegysége a kilopond (kp) volt, ami egy 1 kg tömegű test [[#Súly és súlytalanság|súlya]] (a 45° szélességen, tengerszinten). | |
| − | + | ||
| − | A | + | ==Mechanikai erőhatások== |
| + | ===Nehézségi erő=== | ||
| + | A Földön minden testre hat a nehézségi erő, ami lényegében a Föld gravitációs vonzásából származik (de attól kicsit [[#Gravitációs erő és nehézségi erő|eltér]] a Föld forgása miatt). A nehézségi erő un. térfogati erő: a kiterjedt test minden pontjára hat. Feladatok megoldásánál azonban a testre ható nehézségi erőt egyetlen, a [http://en.wikipedia.org/wiki/Center_of_mass tömegközéppontban] ható erővel vesszük figyelembe. A nehézségi erő arányos a test tömegével: $\vec{F}_g=m\vec{g}$, ahol $g\approx$ 9,81 m/s<math>^2</math>, a Föld felszínének közelében csak kis mértékben változó nagyságú nehézségi gyorsulás. A nehézségi erő iránya definíciószerűen a függőleges irány (ami a forgás miatt nem pontosan a Föld középpontja felé mutat). | ||
| − | A | + | ===Kényszererők=== |
| + | A testek mozgásuk során nem mozoghatnak szabadon: más testek kényszerfeltételeket szabhatnak a test mozgására. Ezek a kényszerek is erők formájában hatnak a testre, ezeket a különböző erőket nevezzük kényszererőknek. | ||
| − | + | Kiterjedt testek nem hatolhatnak akadálytalanul egymásba, ezért egy másik (merev) test felülete kényszerként megakadályozza a test szabad mozgását. A két test felülete közt ható erő a nyomóerő ($\vec{F}_n$). A nyomóerő mindig merőleges a felületre, nagyságát azonban a testre ható más erők és a test mozgása határozza meg. | |
| − | + | ||
| − | + | ||
| − | + | Egy másik, gyakran előforduló kényszererő a fonálerő (kötélerő). Egy fonálra rögzített test mozgását korlátozza a fonál: a testre a többi erő és a test mozgásától függő nagyságú fonálirányú húzó erő hat. | |
| − | === | + | ===Súrlódás, közegellenállás=== |
| − | + | Két test érintkezésekor a felületre merőleges nyomóerőn kívül a felülettel párhuzamos erő is felléphet, ez a súrlódási erő ($\vec{F}_s$). Megkülönböztetünk nyugalmi (tapadási) és mozgási (csúszási) súrlódást. | |
| − | A | + | A tapadási súrlódási erő két egymáshoz képest álló felület közt lép fel. Nagysága és iránya mindig olyan, hogy akadályozza a testek egymáshoz képesti elmozdulását. Nagysága azonban nem lehet tetszőlegesen nagy: $\vec{F}_s\leq\mu_0\vec{F}_n$, ahol $\vec{F}_n$ a felületen ható nyomóerő, $\mu_0$ pedig a felületek anyagától és minőségétől függő tapadási súrlódási együttható. |
| − | + | A csúszási súrlódási erő két egymáshoz képest mozgó felület között hat. Iránya mindig a relatív elmozdulással ellentétes irányú. Nagysága arányos a felületek közt ható nyomóerővel: $\vec{F}_s=\mu\vec{F}_n$, ahol $\mu$ a (szintén a felületek anyagától és minőségétől függő) csúszási súrlódási együttható. Általában $\mu\leq\mu_0$. | |
| − | + | ||
| − | + | ||
| − | A | + | A levegőben (gázokban) vagy folyadékban mozgó testekre ható fékező erő a [http://en.wikipedia.org/wiki/Drag_(physics) közegellenállás] ($\vec{F}_k$). Kis sebességeknél a fékező erőt a gáz (folyadék) és a test közti viszkózus súrlódás okozza, ilyenkor $F_k\sim v$. Nagyobb sebességeknél viszont a mozgó test mögött kialakuló örvények fékezik a testet, ekkor $F_k\sim v^2$. A légellenállás vizsgálatára egy konkrét feladat kapcsán [[#Szabadesés légellenállással|visszatérünk]]. |
| − | + | A relatív sebességgel ellentétes irányú fékező erőn kívül felléphetnek oldalirányú erők is, például a repülésben alapvetően fontos [http://en.wikipedia.org/wiki/Lift-induced_drag aerodinamikai felhajtóerő], vagy a forgó tárgyaknál fellépő [http://en.wikipedia.org/wiki/Magnus_effect Magnus-hatás]. | |
| − | A | + | ==Newton II. törvénye a nanotechnológiában== |
| + | ===A tehetetlenségi piezo mozgató=== | ||
| + | [[Fájl:2001_piezo.jpg|bélyegkép|200px|1. ábra]] | ||
| + | Látványos kísérlet, amit egy kis gyakorlással bárki megcsinálhat: úgy lehet kirántani egy abroszt a teríték alól, hogy a poharak, tányérok éppen csak megmozdulnak. | ||
| − | + | A kísérlet alapja a testek tehetetlensége. Ha egy vízszintes tálcára poharakat állítunk, és a tálcát lassan (kis gyorsulással) mozgatni kezdjük, akkor a tapadási súrlódás miatt a poharak a tálcával együtt fognak mozogni. Ha viszont a tálcát hirtelen (nagy gyorsulással) mozgatjuk, akkor a poharak megcsúsznak, és tehetetlenségük miatt nem követik a tálca mozgását. Ha a tálcát kis kitéréssel, de aszimmetrikusan, az egyik irányban kis gyorsulással, a másik irányba nagy gyorsulással mozgatjuk, akkor elérhetjük, hogy a poharak a tálcán lassan vándoroljanak: egyik irányban a tálcával együtt mindig elmozdulnak egy kicsit, a másik irányban viszont megcsúsznak, és lényegében helyben maradnak. | |
| − | + | Ilyen elven működnek a gyárakban anyagok mozgatására használt rázócsúszdák (ahol megfelelő rezgetéssel akár gyengén felfelé is csúszhatnak a tárgyak), és ugyanezen az elven alapul a tehetetlenségi piezo mozgató, amivel apró tárgyakat akár több cm távolságra el lehet juttatni atomi (tized nm) pontossággal. | |
| − | A | + | A [http://en.wikipedia.org/wiki/Piezoelectricity piezo kristályok] a kristálylapokra kapcsolt feszültség hatására deformálódnak (deformáció hatására pedig feszültség keletkezik rajtuk). A feszültség finom szabályozásával a kristály szabad vége akár tized nm-es pontossággal mozgatható. Az ilyen elven működő különböző [http://en.wikipedia.org/wiki/Scanning_probe_microscopy pásztázó mikroszkópok] segítségével egy anyag felülete atomi felbontással letapogatható. |
| − | + | A piezo kristály szabad vége azonban csak kis elmozdulásokra képes. Nagyobb (cm-es) távolságokra úgy lehet eljuttatni egy apró tárgyat, hogy a kristályra aszimmetrikus (fűrészfog alakú) feszültségjelet kapcsolnak. Így a tárgy az egyik irányban (kis gyorsulással) a súrlódás miatt a kristály végével együtt mozog, a másik irányban viszont megcsúszik a nagy gyorsulással mozgó kristályon, és lényegében helyben marad. Így a kristály (aszimmetrikus) rezgése hatására apró lépésekben egy irányba halad. | |
| − | + | ==Valóságos mozgások modellezése== | |
| + | ===Milyen hatásokat fontos figyelembe venni?=== | ||
| + | Feladatgyűjteményekben gyakran olvasható egy-egy feladat végén, hogy valamilyen hatás (pl. a súrlódás vagy a légellenállás) „elhanyagolható”. | ||
| − | A | + | A valóságban azonban egy fizikai folyamatot ''végtelen'' sok hatás befolyásol kisebb-nagyobb mértékben. (A hőmérséklet- és nyomásváltozásoktól az elektromos és mágneses hatásokon keresztül távoli testek gravitációs hatásáig.) Egy valódi probléma esetében ezért célszerűbb azt vizsgálni, hogy mi az a ''néhány'' hatás, amit a megoldáshoz mindenképp figyelembe kell venni. A súrlódás vagy a légellenállás nagyon sok mozgás esetében meghatározó, és a helyes megoldás érdekében annak ellenére figyelembe kell venni, hogy a megoldást bonyolultabbá teszi. (Mint [[#Szabadesés_légellenállással|látni fogjuk]] a numerikus módszereknek köszönhetően így sem válnak a feladatok megoldhatatlanná.) |
| − | + | Egy-egy konkrét feladat esetében nem mindig könnyű eldönteni, hogy melyek azok a hatások, amelyek semmiképp nem elhanyagolhatók. Ebben egyrészt a gyakorlat, másrészt – szükség esetén – próbaszámítások vagy kísérletek segíthetnek. | |
| − | + | Példaképp vizsgáljuk egy kanyarban haladó autó mozgását. Az egyenletes sebességgel haladó járműnek valamilyen okból hirtelen fékeznie kell. Legfeljebb mekkora lehet a fékezés megkezdésekor a lassulása? Ha állandó erővel fékez, mekkora úton áll meg? Hogyan változik a kerekekre ható súrlódási erő az idő függvényében? | |
| − | + | Milyen hatásokat kell figyelembe venni? A járműre hat a nehézségi erő és a talaj nyomóereje. Az út és a kerekek közti tapadási súrlódás semmiképp nem elhanyagolható, hiszen nélküle se kanyarodni, se fékezni nem lehet. Ennek a problémának a megoldásánál ezeket az erőkkel számolunk. | |
| − | A | + | |
| − | + | A légellenállás általában szintén nem elhanyagolható hatás egy jármű mozgására (hiszen vízszintes úton nagyobb sebességeknél elsősorban emiatt kell egyenletes sebességgel való haladáshoz is nyomni a gázpedált), de a hirtelen fékezéskor fellépő nagy erők mellett ebben az esetben szerepe másodlagos. (Ráadásul nincs információnk a szélről, ami a légellenállást szintén erősen befolyásolja.) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ===A mozgásegyenletek felírása=== | |
| + | [[Fájl:2002_vektorabra.jpg|bélyegkép|200px|2. ábra]] | ||
| + | A mozgásegyenlet felírásához érdemes vázlatot készíteni a testre ható erőkről, ahol a test sebességét, gyorsulását, és a választott koordinátarendszer tengelyeit is feltüntetjük. | ||
| − | A | + | A mi esetünkben a rajzon a vízszintes erőket és irányokat rajzoljuk be (2. ábra), ezen kívül a testre függőleges irányban lefelé az $mg$ nehézségi erő, felfelé pedig az $F_n$ nyomóerő hat. Vízszintes irányban csak a talaj és a kerekek közt fellépő $F_s$ tapadási súrlódási erő hat. A koordinátatengelyeket a jármű haladási irányában előre és erre merőlegesen, a kör középpontja irányában vesszük fel. A test a kanyarodás miatt gyorsul a kör középpontja felé ($a_{cp}$ centripetális gyorsulás) és a fékezés miatt a pálya érintőjének irányában is ($a_t$ tangenciális gyorsulás). |
| − | + | Függőleges irányban a test nem gyorsul (feltesszük, hogy az út vízszintes), így a függőleges irányú erők eredője nulla: $$F_n-mg=0$$ Vízszintes irányban a test gyorsulásvektora a centripetális gyorsulás és a tangenciális gyorsulás erdője: $$\vec{a}=\vec{a}_{cp}+\vec{a}_t$$ A két gyorsulás egymásra merőleges, így $$a=\sqrt{a_{cp}^2+a_t^2}$$ $$a_{cp}=\frac{v^2}{r}$$ ahol $r$ a pálya sugara. Vízszintes irányban csak a súrlódási erő hat, így Newton II. törvénye alapján: $$F_s=ma$$ A tapadási súrlódási erő nem lehet akármilyen nagy: $$F_s\leq\mu F_n$$ | |
| + | Ezeket az egyenleteket és egyenlőtlenségeket kell megoldanunk. | ||
| − | A | + | ===Kezdeti feltételek megadása=== |
| + | A probléma egyértelmű megoldásához a mozgásegyenleteken kívül szükség van a kezdeti feltételek megadására. Ugyanolyan mozgásegyenleteknek egész más megoldása lehet, ha mások a kezdeti feltételek. Például, ha a testre csak a nehézségi erő hat ($m\vec{a}=m\vec{g}$, $\vec{a}=\vec{g}$), akkor a kezdeti feltételektől függően lehet a mozgás szabadesés ($v(0)=0$), függőleges, vízszintes vagy ferde hajítás is. | ||
| − | + | Esetünkben a kezdeti sebesség ($v(0)$) értékére van szükségünk. (Látni fogjuk, hogy ettől függően lehet, vagy nem lehet fékezni.) | |
| − | A | + | ===A mozgásegyenlet megoldása=== |
| + | Az egyenletrendszer könnyen megoldható: $$F_n=mg$$ $$ma=F_s\leq\mu F_n=\mu mg$$ $$a\leq\mu g$$ $$\left|a_t\right|=\sqrt{a^2-a_{cp}^2}\leq\sqrt{(\mu g)^2-\frac{v^4}{r^2}}$$ | ||
| − | A | + | A fékezés kezdetekor a lassulás maximális értéke: $$|a_t|_{max}=\sqrt{(\mu g)^2-\frac{\left[v(0)\right]^4}{r^2}}$$ |
| − | + | Látható, hogy a feladatnak csak akkor van megoldása, ha $$\mu g\geq\frac{\left[v(0)\right]^2}{r}$$ $$v\leq\sqrt{\mu rg}$$ | |
| + | [[Fájl:2003_fekut-kezdetisebesseg2.jpg|bélyegkép|200px|3. ábra]] | ||
| + | [[Fájl:2004_surlodasi_ero-ido.jpg|bélyegkép|200px|4. ábra]] | ||
| − | + | Ha $v>\mu rg$, akkor a jármű már a fékezés előtt, kanyarodás közben megcsúszik, ha $v=\mu rg$ akkor a kanyart még éppen be lehet venni, de fékezni már egyáltalán nem lehet. | |
| − | + | Az állandó fékező erővel elérhető minimális fékút a maximális lassulásból már könnyen kiszámolható: $$v(t)=v(0)+a_t t=v(0)-\left|a_t\right|_{max}t$$ $$v(t)=0\quad\Leftrightarrow\quad t=\frac{v(0)}{\left|a_t\right|_{max}}$$ $$s=v(0)t-\frac{1}{2}\left|a_t\right|_{max}t^2=\frac{\left[v(0)\right]^2}{2\left|a_t\right|_{max}}$$ | |
| + | (A fékerő fokozatos változtatásával a fékút lehet rövidebb: a sebesség csökkenésével csökken a centripetális gyorsulás, és így egyre nagyobb lehet a jármű lassulása.) | ||
| − | + | A súrlódási erő időfüggése: $$F_s=ma=m\sqrt{a_{cp}^2+a_t^2}=m\sqrt{\frac{\left[v(t)\right]^4}{r^2}+|a_t|_{max}^2}$$ | |
| − | + | ||
| − | A sebesség | + | ===A megoldás ábrázolása grafikonokkal=== |
| + | A megoldás grafikonokkal (elmozdulás-idő, sebesség-idő, sebesség-elmozdulás, stb.) vagy animációval tehető szemléletessé. | ||
| − | A | + | A 3. ábra a fékút függését ábrázolja a $v$(0) sebességtől (adatok: $\mu$ = 0,7, $r$ = 40 m). A 4. ábrán a súrlódási erő időfüggése látható (adatok: $v$(0) = 55 km/h, $m$ = 1000 kg). |
| − | == | + | ==Szabadesés légellenállással== |
| − | === | + | ===A feladat megoldása egyszerű numerikus módszerekkel=== |
| − | + | A Földön a szabadon eső testekre a nehézségi erőn kívül (különleges, vákuumban végzett kísérletektől eltekintve) a levegő közegellenállása is hat. A tapasztalat szerint a közegellenállási erő a sebesség növekedésével egyre nagyobb lesz, a test egyre kisebb gyorsulással gyorsul, míg végül – elegendően hosszú esési idő után – állandósult sebességgel, egyenes vonalú egyenletes mozgással esik tovább. Az, hogy a testre ható közegellenállási erő mennyi idő után válik meghatározó hatássá, függ az eső test méretétől, sűrűségétől és alakjától, valamint a közeg (a levegő vagy esetleg más gáz, folyadék) tulajdonságaitól is. Például egy porszem vagy egy ejtőernyős már viszonylag hamar egyenletes sebességgel esik, egy nagyobb kő viszont aránylag sokáig gyorsul. | |
| − | [ | + | Az eső testre a nehézségi erő és a közegellenállás hat, a mozgásegyenlet könnyen felírható. (A mozgás egyenes vonalú, így nincs szükség vektoregyenletre. A pozitív irányt függőlegesen lefelé választottuk.) $$ma=mg-F_k$$ |
| + | Az $F_k$ közegellenállási erő nagysága függ a test méretétől, alakjától, sebességétől, valamint a közeg tulajdonságaitól is. Aránylag kis sebességeknél a testre ható fékező erőt a közeg viszkozitása (belső súrlódása) okozza. Ilyen eset például egy apró porszem esése levegőben, vagy egy kanál süllyedése mézben Ekkor az erő a test sebességével arányos, gömb alakú test estében például $F_k=6\pi\eta rv$, ahol $r$ a gömb sugara, $\eta$ pedig a közeg viszkozitása ([http://en.wikipedia.org/wiki/Stokes%27_law Stokes-törvény]). | ||
| − | + | Nagyobb sebesség esetén a testet a mögötte kialakuló örvények fékezik. Ez a meghatározó effektus, ha porszemnél nagyobb tárgyak esnek levegőben vagy vízben. Ilyenkor a fékező erő a sebesség négyzetével arányos: $$F_k=\frac{1}{2}\rho v^2cA$$ ahol $\rho$ a közeg sűrűsége, $A$ a test keresztmetszete, $c$ pedig a dimenziótlan formatényező. | |
| − | + | Ha az utóbbi modellt használjuk, és a közegellenállási erőt röviden $F_k=kv^2$ alakban írjuk (ahol $k$ egy állandó, amely csak a test méretétől és alakjától, valamint a közeg sűrűségétől függ), akkor a mozgásegyenlet: $$ma=mg-kv^2$$ | |
| − | + | [[Fájl:2005_v-t_grafikon.jpg|bélyegkép|200px|5. ábra]] | |
| + | [[Fájl:2006_a-t_grafikon.jpg|bélyegkép|200px|6. ábra]] | ||
| + | [[Fájl:2007_numerikus_pontossag.jpg|bélyegkép|200px|7. ábra]] | ||
| + | |||
| + | Itt azonban $a$ és $v$ nem ismeretlen (időben állandó) mennyiségek, hanem ismeretlen függvények: $a(t)$ és $v(t)$. A mozgásegyenlet, amit felírtunk, egy függvényegyenlet: $$ma(t)=mg-k\left[v(t)\right]^2$$ $a(t)$ és $v(t)$ azonban nem függetlenek egymástól: $$a(t)=\frac{{\rm d}v(t)}{{\rm d}t}$$ $$\frac{{\rm d}v(t)}{{\rm d}t}=g-\frac{k}{m}\left[v(t)\right]^2$$ Ez az egyenlet egy differenciálegyenlet, amely az ismeretlen függvényen kívül annak deriváltját (deriváltjait) is tartalmazza. A differenciálegyenletek egyes esetekben analitikusan megoldhatók, más esetekben viszont a megoldást csak numerikus módszerekkel lehet meghatározni. Bár a fenti differenciálegyenletnek létezik analitikus [http://en.wikipedia.org/wiki/Drag_(physics)#Velocity_of_a_falling_object megoldása] is, most oldjuk meg numerikus módszerekkel! | ||
| − | + | Differenciálegyenletek numerikus megoldására [http://en.wikipedia.org/wiki/List_of_numerical_analysis_topics#Numerical_ordinary_differential_equations nagyon sok] módszer van, itt most egy nagyon egyszerű, fizikai szempontból szemléletes megoldást mutatunk be. | |
| − | + | Ha ismerjük a test $x(t)$ helyét és $v(t)$ sebességét egy $t$ időpontban, akkor a mozgásegyenlet alapján ki tudjuk számítani a gyorsulását is: $$a(t)=g-\frac{k}{m}\left[v(t)\right]^2$$ A gyorsulás egy elegendően kicsi $\Delta t$ időtartam alatt keveset változik, ezért a test sebességét és helyét a $t\!\!+\!\!\Delta t$ időpontban jó közelítéssel ki tudjuk számolni úgy, mintha egyenletesen gyorsuló mozgás lenne: $$v(t\!\!+\!\!\Delta t)\approx v(t)+a(t)\Delta t$$ $$x(t\!\!+\!\!\Delta t)\approx x(t)+v(t)\Delta t+\frac{1}{2}a(t)(\Delta t)^2$$ $x(t\!\!+\!\!\Delta t)$ és $v(t\!\!+\!\!\Delta t)$ ismeretében már meghatározható $a(t\!\!+\!\!\Delta t)$, és az eljárás megismételhető. | |
| − | + | A számítás elvégzéséhez szükség van a kezdeti feltételek ($x(0)$ és $v(0)$), valamint a befejezés feltételének megadására (például a vizsgált időtartam, vagy a földetérés távolságának a megadására). Ezen kívül meg kell választani $\Delta t$ értékét. Túl nagy $\Delta t$ választása esetén a számítás pontatlan, túl kicsi érték viszont feleslegesen hosszú számítási időt eredményez. | |
| − | + | A számítás az algoritmus alapján bármely programnyelvvel (akár excel táblázatkezelővel is) elvégezhető, a mozgás grafikonokkal vagy animációval szemléltethető. | |
| − | + | Az 5. és 6. ábrán látható grafikonok egy 100 m magasról leeső focilabda sebességét és gyorsulását ábrázolják az idő föggvényében (adatok: $m$ = 0,435 kg, $d$ = 0,22 m, $\rho$ = 1,2 kg/m<math>^3</math>, c = 0,47). Jól látható, hogy a gyorsulás a kezdeti $g$ értékről indulva nullához, a sebesség pedig egy határértékhez (az állandósult sebességhez) tart. A határsebesség a mozgásegyenletből kifejezhető: $$v_\infty=\sqrt{\frac{mg}{k}}$$ | |
| − | + | Az adatokat behelyettesítve ez esetünkben kb. 20 m/s (72 km/h). | |
| − | + | ===A numerikus megoldás veszélyei=== | |
| + | A numerikus megoldás minden lépése közelítő, a kicsiny hibák idővel felhalmozódnak, a számítás eredménye egyre távolabb kerülhet az egzakt megoldás eredményétől. [[Rezgések#A kaotikus viselkedés jellemzői és feltételei|Kaotikus]] rendszerek különösen érzékenyek erre. A lépésköz csökkentésével a hiba csökkenthető (7. ábra) – ez viszont bonyolultabb számításoknál a program futási idejét növelheti meg túlságosan. | ||
| − | [[ | + | Bizonyos esetekben lehetőség van a felhalmozódó hibák részleges kijavítására is. Például ha a rendszerben a [[Megmaradási törvények a mechanikában#A mechanikai energia megmaradásának tétele|teljes mechanikai energia]] állandó, akkor ezt a feltételt is figyelembe lehet venni a számításban, és ezzel el lehet kerülni, hogy a numerikus megoldásban az összenergia folyamatosan növekedjen vagy csökkenjen. |
| − | [http://en.wikipedia.org/wiki/ | + | ==Newton gravitációs törvénye== |
| − | + | ===A törvény „ellenőrzése”=== | |
| + | [http://en.wikipedia.org/wiki/Isaac_Newton Newton] nevéhez kötődik a róla elnevezett törvényeken kívül a [http://en.wikipedia.org/wiki/Gravitation gravitációs kölcsönhatás] leírása is. Az általános tömegvonzás törvényének megalkotásához Newtont két fontos tapasztalat segítette: [http://en.wikipedia.org/wiki/Galileo_Galilei Galilei] kísérletekkel igazolt állítása, miszerint a szabadon eső testek gyorsulása (ha a légellenállást elhanyagolható) nem függ a testek tömegétől, és [http://en.wikipedia.org/wiki/Johannes_Kepler Kepler] [http://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion#Third_law III. törvénye], amely az égitestek keringési ideje és a pályájuk fél nagytengelye között teremt kapcsolatot. | ||
| − | + | Ezekből a tapasztalatokból, figyelembe véve [[##Newton II. törvénye|Newton II. törvényét]] következik, hogy a tömegvonzás egyenesen arányos a kölcsönhatásban résztvevő testek tömegével és fordítva arányos a testek távolságának négyzetével. Így a gravitációs erő nagysága $$F_g=\gamma\frac{m_1 m_2}{r^2}$$ ahol $m_1$ és $m_2$ a testek tömege,$r$ a két tömegpont távolsága (kiterjedt testeknél, ha a testek gömbszimmetrikusak, a gömbök középpontjának távolsága), $\gamma$ pedig egy egyelőre ismeretlen állandó. Az erő mindig vonzóerő, iránya a két testet összekötő egyenes. | |
| − | + | Newton a törvény ellenőrzésére a Föld felszínének közelében szabadon eső test és a Föld körül első közelítésben körpályán keringő Hold mozgását hasonlította össze. Végezzük el mi is ezt az ellenőrzést! | |
| − | = | + | A szabadon eső testre (elhanyagolva a légellenállást) csak a Föld gravitációs ereje hat: $$F=\gamma\frac{m m_F}{r_F^2}$$ ahol $m_F$ a Föld tömege, $r_F$ pedig a Föld sugara (hiszen a Föld felszínén lévő test ilyen távolságra van a Föld középpontjától). A testre felírt mozgásegyenlet (elhanyagolva, hogy a Föld forog): $$F=mg$$ A két egyenletből $$\gamma\frac{m m_F}{r_F^2}=mg$$ $$\gamma m_F=g r_F^2$$ |
| − | + | A Hold és a Föld között fellépő gravitációs erő: $$F_H=\gamma\frac{m_H m_F}{r_H^2}$$ ahol $m_H$ a Hold tömege, $r_H$ pedig a Föld-Hold távolság (a középpontjaik közti távolság). A Hold első közelítésben körpályán mozog a Föld körül, így a mozgásegyenlet: $$F_H=m_H a_cp$$ ahol $a_cp$ a Hold centripetális gyorsulása. A két egyenletből $$\gamma\frac{m_H m_F}{r_H^2}=m_H a_cp$$ $$\gamma m_F=a_cp r_H^2$$ A centripetális gyorsulás $$a_cp=r_H \omega_H^2=r_H\frac{4\pi^2}{T_H^2}$$ ahol $\omega_H$ a Hold keringésének szögsebessége,$T_H$ pedig a Hold keringési ideje. Ezt behelyettesítve $$\gamma m_F=\frac{4\pi^2}{T_H^2}r_H^3$$ | |
| − | + | A képletekben szereplő $g$, $r_F$, $r_H$ és $T_H$ értékeket már Newton is ismerhette. A Föld-Hold távolságot a [[Tér_és_idő#A_méter_eredeti_definíciója|Föld sugarához]] hasonlóan már az ókorban megmérték [http://en.wikipedia.org/wiki/Parallax#Lunar_parallax parallaxis] módszerrel (a Hold a Föld különböző pontjairól más irányban látszik), közepes értéke a Föld sugarának kb. 60-szorosa. A Hold keringési ideje, az un. [http://en.wikipedia.org/wiki/Month#Sidereal_month sziderikus hónap], az az idő, ami alatt a Hold az állócsillagokhoz képest egyszer megkerüli a Földet. (Ez az idő – 27,32 nap – eltér a két azonos holdfázis, pl. két telihold közti [http://en.wikipedia.org/wiki/Month#Synodic_month szinodikus hónaptól] – 29,53 nap –, hiszen miközben a Hold megkerüli a Földet, a Föld is elmozdul a Nap körül.) | |
| − | + | Behelyettesítve a $g=9,81\,{\rm m/s^2}$, az $r_F=6,37\cdot 10^6\,{\rm m}$, az $r_H=3,84\cdot 10^8\,{\rm m}$ és a $T_H=27,52\,{\rm nap}=2,36\cdot 10^6\,{\rm s}$ értékeket $\gamma m_F$ két kifejezésébe. a $$\gamma m_F=g r_F^2=3,98\cdot 10^{14}\,{\rm m^3/s^2}$$ illetve a $$\gamma m_F=\frac{4\pi^2}{T_H^2}r_H^3=4.01\cdot 10^{14}\,{\rm m^3/s^2}$$ értékek adódnak, amelyek kevesebb, mint 1 %-kal térnek el egymástól. Figyelembe véve a számítás közben végzett elhanyagolásokat, ez valóban meggyőző eredmény. | |
| − | + | ||
| − | + | ||
| + | ===Súly és súlytalanság=== | ||
| + | A [http://en.wikipedia.org/wiki/Weight súly] és a tömeg fogalma a hétköznapi szóhasználatban gyakran keveredik, egymás szinonimájaként használják. Pedig a két fogalom között (azon kívül, hogy a súly egy erő, tehát mértékegységét tekintve is különbözik a tömegtől) jelentős különbségek vannak. A test súlya a tömegén kívül függ a test helyétől és mozgásállapotától is. | ||
| − | + | A súly [http://en.wikipedia.org/wiki/Weight#Definitions meghatározása] a nemzetközi irodalomban nem egységes. A Magyarországon szokásos meghatározás szerint egy test súlya az az erő, amelyet a test az alátámasztására vagy a felfüggesztésére kifejt. Azt, hogy egy testnek súlya van, a rá ható gravitációs erő okozza, így az függ a test helyén mérhető nehézségi gyorsulástól. Ezért lesz egy test súlya kisebb a Holdon, mint a Földön (körülbelül egy hatoda a földi súlyának). A test súlya azonban csak akkor egyezik meg a rá ható gravitációs erővel, ha a test nyugalomban van (vagy egyenes vonalú egyenletes mozgást végez). Ha a test gyorsul, akkor a rá ható erők eredője nem nulla, és a test súlya különbözni fog a gravitációs erőtől. | |
| + | Egyszerű méréseket lehet végezni egy liftben. Ha a nyugalomban lévő (vagy egyenletesen haladó) liftben ráállunk egy fürdőszobamérlegre, akkor az az „igazi”, nyugalmi súlyunkat fogja mutatni, $F_n=mg$. Ha viszont a lift felfelé gyorsuló mozgást végez (felfelé gyorsít, vagy lefelé fékez), akkor a testünket a mérleg által kifejtett nyomóerő és a gravitációs erő különbsége fogja gyorsítani ($ma=F_n-mg$), tehát a súlyunk (az az erő, amit a testünk kifejt az alátámasztásra – az alátámasztás által kifejtett nyomóerő ellenereje) nagyobb lesz a nyugalomban mért súlynál: $F_n=m(g+a)$. Ehhez hasonlóan lefelé gyorsuló liftben (ha a lift lefelé gyorsít, vagy felfelé fékez) a súlyunk kisebb lesz: $F_n=m(g-a)$. | ||
| − | + | Ha egy test szabadon esik, vagy más olyan mozgást végez, ahol a gravitáción kívül nem hat rá más erő (például kering a Föld körül), akkor a súlya nulla lesz. Ez a [http://en.wikipedia.org/wiki/Weightlessness súlytalanság] állapota. Természetesen a gravitáció a súlytalanság állapotában is hat a testre: a Föld körül keringő testet például éppen a gravitáció tartja körpályán (a gravitációs erő okozza a test centripetális gyorsulását). | |
| − | + | ===Mekkora a Föld tömege? A gravitációs állandó mérése=== | |
| + | Mekkora a Föld tömege? Ha tudnánk, akkor abból a $\gamma$ gravitációs állandót is ki lehetne számítani, hiszen [[#Newton gravitációs törvénye|korábban]] kiszámítottuk a két mennyiség szorzatát. A Föld tömegét azonban nem tudjuk másképp meghatározni, csak éppen a gravitációs hatásán keresztül. Így először a $\gamma$ állandót kell valahogy megmérni, és a Föld tömegét majd az alapján meghatározni. (A gravitációs állandó meghatározásához hasonlóan alkalmatlan a bolygók Nap körüli keringésének vizsgálata, hiszen a Nap tömegét se ismerjük független mérésből.) | ||
| − | + | A $\gamma$ gravitációs állandó értékét két ismert tömegű és ismert távolságú test közt fellépő erőhatás alapján lehet megmérni. Mivel hétköznapi méretű testek között ez az erőhatás más erőkhöz képest nagyon kicsi, a mérés elvégzése nem könnyű. A XVIII. század legvégén elvégzett [http://en.wikipedia.org/wiki/Cavendish_experiment Cavendish-kísérlet] lényege, hogy a kicsiny erőt egy torziós szál elcsavarodásából lehet meghatározni. [http://en.wikipedia.org/wiki/Henry_Cavendish Cavendish] egy vízszintes rúd végeire két egyforma, néhány kg tömegű ólomgolyót rögzített, a rudat pedig egy vékony, rugalmas szálra függesztette ([http://en.wikipedia.org/wiki/Torsion_spring#Torsion_balance torziós inga]). A felfüggesztett testek mellé helyezett másik két ólomgömb vonzásának hatására a szál kis mértékben elcsavarodott, amiből a szál [http://en.wikipedia.org/wiki/Torsion_spring#Torsion_coefficient torziós együtthatójának] és a mérés geometriai elrendezésének ismeretében a fellépő gravitációs erő és a [http://en.wikipedia.org/wiki/Gravitational_constant gravitációs állandó] értéke kiszámítható: $\gamma=6,67\cdot 10^{-11}\,{\rm Nm^2/kg^2}$. | |
| − | + | A gravitációs állandó alapján már kiszámítható a Föld tömege és átlagos sűrűsége: $$m_F=\frac{g r_F^2}{\gamma}=5,97\cdot10^{24}\,{\rm kg}$$ $$\rho_F=\frac{m_F}{V_F}=5510\,{\rm kg/m^3}$$ | |
| − | + | A gravitációs állandó ismeretében a Föld (vagy más bolygók) pályaadataiból ehhez hasonlóan meghatározható a Nap tömege és sűrűsége is. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | ==Newton I. törvénye== | ||
| + | ===Az inerciarendszer fogalma=== | ||
| + | Newton I. törvénye kimondja, hogy ha egy testre nem hat erő, vagy a rá ható erők eredője 0, akkor a test nyugalomban van, vagy egyenes vonalú egyenletes mozgást végez. $$\Sigma \vec{F}=0\quad\Leftrightarrow\quad\vec{v}={\rm const.}$$ Newton I. törvénye a II. törvény speciális esetének is tekinthető, hiszen $$\Sigma\vec{F}=0\quad\Leftrightarrow\quad\vec{a}=\frac{\Sigma\vec{F}}{m}=0\quad\Leftrightarrow\quad\vec{v}={\rm const}$$ | ||
| + | A törvény állításával („nyugalomban van”, „egyenes vonalú egyenletes mozgást végez”) kapcsolatban azonban fel kell tennünk egy kérdést: Mihez képest? Milyen koordinátarendszerhez képest van a test nyugalomban? Milyen koordinátarendszerhez képest végez egyenes vonalú egyenletes mozgást? | ||
| − | + | Hétköznapi tapasztalat, hogy egy hirtelen fékező járműben a járműhöz képest korábban nyugalomban lévő test látszólag minden ok nélkül gyorsulni kezd. A járműhöz rögzített koordinátarendszerben ez ellentmond Newton I. törvényének: a test ebből a koordinátarendszerből nézve annak ellenére gyorsul, hogy a rá ható erők eredője nulla. Ugyanakkor, ha a Földhöz rögzített koordinátarendszerben írjuk le a mozgást, akkor azt látjuk, hogy a jármű fékez (lassul, negatív gyorsulása van), a test viszont egyenes vonalú egyenletes mozgással halad tovább, összhangban Newton I. törvényével. | |
| − | + | ||
| − | + | ||
| − | + | Hasonló a helyzet egy kanyarodó járműben. A járműhöz rögzített koordinátarendszerből vizsgálva a járműben lévő testek annak ellenére kifelé (a kanyarodással ellentétes irányban) gyorsulnak, hogy nem hat rájuk vízszintes erő – ismét ellentmondva Newton I. törvényének. A Földhöz rögzített koordinátarendszerből nézve viszont azt látjuk, hogy a járművön lévő testek – összhangban Newton I. törvényével – egyenes vonalú egyenletes mozgással haladnak tovább, miközben a jármű „elkanyarodik alóluk”. Eszerint vannak olyan koordinátarendszerek, amelyekből leírva a jelenségeket Newton I. törvénye teljesül, és vannak olyanok, [[#Gyorsuló_és_forgó_koordinátarendszerek|amelyekben nem]]. | |
| − | + | Azokat a koordinátarendszereket, melyekben teljesül Newton I. törvénye (azaz ha egy testre nem hat erő, vagy a rá ható erők eredője nulla, akkor a test ebben a koordinátarendszerben nyugalomban van, vagy egyenes vonalú egyenletes mozgást végez), ''inerciarendszer''nek nevezzük. Newton I. törvénye így nem más, mint az [http://en.wikipedia.org/wiki/Inertial_frame inerciarendszer] definíciója. A Newton-törvények – eredeti formájukban – csak inerciarendszerekben igazak. | |
| − | + | A definíció alapján látszólag könnyű eldönteni, hogy egy koordinátarendszer inerciarendszer-e. Azonban azt, hogy egy testre valóban semmilyen erő ne hasson, nehéz biztosítani. Sok feladat megoldásakor a Földhöz rögzített koordinátarendszer inerciarendszernek tekinthető. A Föld azonban forog, így a Földhöz képest nyugalomban lévő testek valójában körmozgást végeznek a Föld tengelye körül, és így gyorsulnak. Tehát a Földhöz rögzített koordinátarendszer [[#Tehetetlenségi erők a forgó Földön|nem inerciarendszer]]. (A forgás lassú, ezért lehet sok esetben mégis annak tekinteni.) Jobb közelítés a Föld középpontjához rögzített, de nem forgó rendszer. Ez azonban a Föld Nap körüli keringése miatt – sokkal kisebb mértékben – szintén gyorsul. A Nap középpontjához (pontosabban a Naprendszer tömegközéppontjához) rögzített koordinátarendszer már gyakorlatilag minden esetben inerciarendszerként használható. | |
| − | + | ||
| − | + | A [http://en.wikipedia.org/wiki/Galilean_invariance Galilei-féle relativitás elve] alapján az egymáshoz képest nyugalomban lévő vagy egyenes vonalú egyenletes mozgást végző rendszereket mechanikai jelenségek alapján nem lehet megkülönböztetni. Így ha egy koordinátarendszer inerciarendszer, akkor a hozzá képest egyenes vonalú egyenletes mozgást végző test is inerciarendszer. Az inerciarendszerek közötti transzformáció a [http://en.wikipedia.org/wiki/Galilean_transformation Galilei-transzformáció]. | |
| − | A | + | |
| − | + | ||
| − | |||
| − | + | ==Gyorsuló és forgó koordinátarendszerek== | |
| − | + | ===Tehetetlenségi erő=== | |
| − | + | A Newton-törvények eredeti formájukban csak inerciarendszerekben igazak. A [[#Az inerciarendszer fogalma|korábban elemzett példákban]] a fékező vagy kanyarodó járművön lévő testek annak ellenére gyorsuló mozgást végeznek a járműhöz képest, hogy a rá ható erők eredője nulla. A járműhöz képest a fékező (menetiránnyal ellentétes irányban gyorsuló) járműben előrefelé, a kanyarodó (az ív középpontja felé gyorsuló) járműben pedig kifelé gyorsulnak. A járműhöz viszonyított, gyorsuló koordinátarendszerben vizsgálva a testek tehát úgy mozognak, ''mintha'' fékezéskor előrefelé, kanyarodáskor kifelé (általában pedig a jármű gyorsulásával ellentétes irányba) ható erők is hatnának rájuk. | |
| − | + | ||
| − | + | Ezeket a fiktív (nem valóságos) erőket [http://en.wikipedia.org/wiki/Fictitious_force tehetetlenségi erőknek] nevezzük. Bevezetésükkel a Newton-törvények gyorsuló koordinátarendszerekben is használhatóvá válnak: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Ha egy K inerciarendszerben egy pont helyét az $\vec{r}(t)$ helyvektor adja meg, a hozzá képest egyenes vonalú gyorsuló mozgást végző K' rendszerben pedig az $\vec{r}\,'(t)$, akkor a két vektor között az $$\vec{r}(t)=\vec{r}\,'(t)+\vec{r}_{K'}(t)$$ összefüggés teremt kapcsolatot, ahol $\vec{r}_{K'}(t)$ a K' rendszer origójának a helye a K rendszerhez viszonyítva. Ha a kifejezést kétszer deriváljuk idő szerint, akkor az $$\vec{a}(t)=\vec{a}\,'(t)+\vec{a}_0$$ összefüggést kapjuk, ahol $\vec{a}_0$ a K' rendszer gyorsulása a K rendszerhez képest. Az egyenlet mindkét oldalát megszorozva a tömegpont $m$ tömegével, és kihasználva, hogy a tömegpontra ható erők eredője a K inerciarendszerben $\vec{F}_e=m\vec{a}$, az $$\vec{F}_e=m\vec{a}\,'+m\vec{a}_0$$ | |
| + | egyenletet kapjuk. Ez azt mutatja, hogy a gyorsuló K' rendszerben nem teljesül Newton II. törvénye. | ||
| − | + | Ha azonban bevezetjük az $\vec{F}_t=-m\vec{a}_0$ tehetetlenségi erőt, akkor $$\vec{F}_e=m\vec{a}\,'-\vec{F}_t$$ $$\vec{F}_e'=\vec{F}_e | |
| − | + | +\vec{F}_t=m\vec{a}\,'$$ azaz ha a valódi erők mellett a fiktív (nem valóságos) tehetetlenségi erőt is beleszámítjuk az eredő erőbe ($\vec{F}_e'$), akkor a Newton II. törvény ebben a koordinátarendszerben is használhatóvá válik. | |
| − | \ | + | |
| − | \ | + | |
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | \ | + | |
| − | \ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ===Centrifugális erő és Coriolis-erő=== | |
| − | + | Forgó koordinátarendszer esetében a gyorsuló koordinátarendszerhez hasonlóan fiktív tehetetlenségi erők bevezetésével érhetjük el, hogy a Newton-törvények használhatók legyenek. | |
| − | + | Ha a K' rendszer $\vec{\omega}$ szögsebességgel forog a K inerciarendszerhez képest, akkor a K' rendszerben a valódi erőkön kívül általános esetben három fiktív erőt kell felvenni: | |
| − | + | ||
| − | + | ||
| − | + | Az $\vec{F}_{cf}=-m\vec{\omega}\times(\vec{\omega}\times\vec{r})$ [http://en.wikipedia.org/wiki/Centrifugal_force_(rotating_reference_frame) centrifugális erő] minden testre „hat”, az $\vec{F}_{cor}=-2m\vec{\omega}\times\vec{v}$ [http://en.wikipedia.org/wiki/Coriolis_force Coriolis-erő] viszont csak a K' rendszerhez képest mozgó testekre. Az [http://en.wikipedia.org/wiki/Euler_force Euler-erő] bevezetésére csak gyorsulva forgó koordinátarendszer esetén van szükség, ezzel nem foglalkozunk. | |
| − | A | + | A kifejezésekben az $\vec{\omega}$ a [http://en.wikipedia.org/wiki/Angular_velocity szögsebesség-vektor] (ennek nagysága a szögsebesség, iránya pedig a forgás tengelye), a $\times$ jel pedig a [http://en.wikipedia.org/wiki/Vector_cross_product vektoriális szorzat] jele. Ezeknek a tehetetlenségi erőknek a használatát a [[#Tehetetlenségi erők a forgó Földön|forgó Földhöz]] rögzített koordinátarendszer esetében mutatjuk meg. |
| − | + | A [http://www.csodakpalotaja.hu Csodák palotájában] a Coriolis-erő közvetlenül is megtapasztalható a [http://videosmart.hu/video/csodak-palotaja-coriolis-szoba Coriolis-szobában]. A centrifugális erő élményéről pedig Truffaut Négyszáz csapás című filmjében van egy szép [http://v.youku.com/v_show/id_XMTcxMDY2NTQ0.html jelenet]. | |
| − | [http://hu. | + | |
| − | + | ===Valódi erők és tehetetlenségi erők=== | |
| + | A valódi erők és a gyorsuló koordinátarendszereknél bevezetett fiktív tehetetlenségi erők között lényeges különbségek vannak. | ||
| − | + | A valódi erők mindig két test közötti kölcsönhatás kifejezői. Mindig megtalálható az a másik test, amivel a vizsgált test kölcsönhat, és mindig teljesül Newton III. törvénye (hatás-ellenhatás). | |
| − | + | ||
| − | + | ||
| − | A | + | A tehetetlenségi erők fiktív, nem valóságos erők. Gyorsuló koordinátarendszerekben azért vezetjük be, hogy Newton II. törvénye használható legyen. Ezek nem kölcsönhatást fejeznek ki, nem lehet megtalálni a kölcsönható másik testet. Ugyanakkor a gyorsuló koordinátarendszerben leírva a mozgást ezek az erők ugyanúgy hatnak a testekre, mint a valóságos erők. |
| − | + | ==Tehetetlenségi erők a forgó Földön== | |
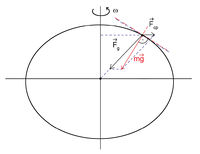
| + | ===Gravitációs erő és nehézségi erő=== | ||
| + | [[Fájl:2008_nehezsegi_ero.jpg|bélyegkép|200px|8. ábra]] | ||
| + | A forgó Föld nem inerciarendszer, azonban a földi jelenségeket mégis legtöbbször a Földhöz rögzített koordinátarendszerben érdemes leírni. Ahhoz, hogy a Newton-törvények használhatók legyenek, a testekre ható valódi erőkön kívül a forgás miatt fellépő fiktív, tehetetlenségi erőket: a centrifugális erőt és Coriolis-erőt is figyelembe kell venni. (A Föld forgása jó közelítéssel egyenletes, így Euler-erő nem lép fel. A Föld Nap körüli keringésének hatása pedig legtöbbször elhanyagolható.) | ||
| − | A | + | A két erő közül a centrifugális erő okoz kevesebb problémát: ennek az erőnek a nagysága nem függ a test mozgásállapotától. A centrifugális erő sok szempontból hasonlóan viselkedik, mint a gravitációs erő, hiszen arányos a test tömegével, és ezen kívül csak a test helyétől függ: $F_{cp}=mr\omega_F^2$, ahol $\omega_F$ a Föld szögsebessége, $r$ pedig a test távolsága a Föld forgástengelyétől. |
| − | + | A forgó koordinátarendszerből megfigyelve nem lehet szétválasztani a két erőt, minden testre a két erő eredője hat. A gravitációs erő ($\vec{F}_g$) a Föld középpontja felé, a centrifugális erő ($\vec{F}_{cp}$) pedig a forgástengelyre merőleges irányban, kifelé mutat. A két erő eredője az $m\vec{g}$ nehézségi erő (8. ábra). A nehézségi erő és a gravitációs erő tehát (a sarkokat kivéve) kis mértékben eltér egymástól, a legnagyobb (kb. 0,3 %) eltérés az egyenlítőnél van. A két erőnek általában az iránya is eltér egymástól: a nehézségi erő a sarkokat és az egyenlítőt kivéve nem a Föld középpontjába mutat. A nehézségi erő iránya definíció szerint az adott helyen a függőleges irány, az erre merőleges sík pedig a vízszintes. A tengerszint – amihez a földrajzi magasságokat mérik – emiatt nem gömbfelület, hanem egy lapult forgási ellipszoid. | |
| − | + | ||
| − | + | ||
| − | A | + | ===Súlyos és tehetetlen tömeg, az Eötvös-kísérlet=== |
| + | A tömeg két alapvető fizikai összefüggésben is szerepel: [[#Newton_II._törvénye|Newton II. törvényében]] és az [[#Newton_gravitációs_törvénye|általános tömegvonzás törvényében]] is. | ||
| − | + | A tömeg fogalmát Newton II. törvénye kapcsán vezettük be: az $\vec{F}=m\vec{a}$ összefüggés megadja, hogy mekkora erő kell egy test gyorsításához. Az összefüggés alapján a tömeget definiálhatjuk a következőképpen: egységnyi tömeg az, amit egységnyi erő egységnyi gyorsulással gyorsít. Ebben a definícióban a tömeg a test „tehetetlenségét” fejezi ki, ezért szokás [http://en.wikipedia.org/wiki/Mass#Inertial_mass tehetetlen tömegnek] nevezni. | |
| − | + | A Newton-féle gravitációs törvény két tetszőleges test közötti vonzóerőt adja meg. Ez az erő a tapasztalat szerint a testek távolságán kívül a testek tömegétől függ. A törvény alapján a tömeget definiálhatjuk a következőképpen is: egységnyi tömeg az, ami egy másik ugyanekkora tömeget egységnyi távolságból megadott erővel (az SI rendszerben 6,67∙10<math>^{-11}</math> N) vonz. Ebben a definícióban a tömeg a test „gravitálóképességét” fejezi ki, ami a gyakorlatban a test súlyát okozza, ezért szokás [http://en.wikipedia.org/wiki/Mass#Newtonian_Gravitational_mass_2 súlyos tömegnek] nevezni. | |
| − | és a | + | Elméleti és gyakorlati szempontból is fontos, hogy a két, egymástól független definícióval meghatározott tömeg ekvivalens-e. Az a kísérleti tapasztalat, hogy vákuumban minden test ugyanakkora gyorsulással esik, azt mutatja, igen: a testre ható gravitációs erő a test $m_s$ súlyos tömegével arányos, a Newton törvényben viszont a test $m_t$ tehetetlen tömege szerepel. A szabadon eső test gyorsulása tehát $$a=\frac{m_s g}{m_t}=\frac{m_s}{m_t}g$$ ami csak akkor lesz minden testre ugyanakkora, ha a kétféle tömeg aránya minden testnél ugyanakkora (megfelelő mértékegység választással 1). |
| − | A | + | A szabadon eső testek gyorsulása azonban nem mérhető kellő pontossággal. [http://hu.wikipedia.org/wiki/E%C3%B6tv%C3%B6s_Lor%C3%A1nd Eötvös Loránd] a XX. század elején a róla elnevezett [http://hu.wikipedia.org/wiki/E%C3%B6tv%C3%B6s_Lor%C3%A1nd#E.C3.B6tv.C3.B6s-inga_.28torzi.C3.B3s_inga.29 Eötvös-inga] segítségével a kétféle tömeg ekvivalenciáját közel három nagyságrenddel pontosabban igazolta, mint a korábbi mérések. Az [http://en.wikipedia.org/wiki/E%C3%B6tv%C3%B6s_experiment Eötvös-kísérlet] alapja, hogy a forgó Földön a vékony torziós szálra erősített tömegekre a súlyos tömegekkel arányos gravitációs erő és a tehetetlen tömegekkel arányos centrifugális erő is hat. Eötvösnek sikerült kimutatnia, hogy a kétféle tömeg aránya különböző anyagok esetén legfeljebb 1:10<math>^{-9}</math> arányban tér el egymástól. |
| − | + | Az Eötvös-ingával mérni lehet a gravitációs erő nagyon kicsiny változásait is, amiből a földalatti tömegeloszlásra lehet következtetni, és így földgáz- és kőolajlelőhelyeket lehet megtalálni. | |
| − | + | ===Coriolis-erő: szelek, tengeráramlatok, folyók=== | |
| + | A Coriolis-erő csak a forgó koordinátarendszerhez képest mozgó testekre hat. Nagysága és iránya függ a test sebességétől, így nem lehet a centrifugális erőhöz hasonlóan kezelni. | ||
| − | A | + | A Coriolis-erő vektoriális kifejezéséből ($\vec{F}_{cor}=-2m\vec{\omega_F}\times\vec{v}$) látszik, hogy az erő merőleges a Föld forgástengelyére és a test Földhöz viszonyított sebességére is, és minden olyan testnél fellép, amely nem a forgástengellyel párhuzamosan mozog. A Coriolis-erőnek számtalan hétköznapi életben megfigyelhető hatására van: a gyorsan mozgó lövedékek a kilövés irányától függően vízszintes és függőleges irányban is eltérülhetnek, a keleti és nyugati irányban mozgó testek súlya kis mértékben eltér egymástól, a szabadon eső testek pedig nem pontosan függőlegesen esnek. |
| − | + | A gyakorlati szempontból legfontosabb jelenség azonban a mozgó levegő- és víztömegekre ható Coriolis-erő. A nyomáskülönbségek miatt mozgó légtömegek a Coriolis-erő hatására eltérülnek, és hatalmas forgó rendszerek, úgynevezett [http://en.wikipedia.org/wiki/Cyclone ciklonok] alakulnak ki. Az északi féltekén a forgás mindig óramutató járásával ellentétes, a délin pedig megegyező irányú. A Coriolis-erőnek fontos szerepe van a trópusokon a felszín közelében kelet felől fújó [http://en.wikipedia.org/wiki/Trade_wind passzát szelek] és a nagy magasságban a Földet körülérő nyugati irányú [http://en.wikipedia.org/wiki/Jet_stream futóáramlások (jetek)] kialakulásában is. | |
| − | + | ||
| − | A | + | A Coriolis-erő a légtömegekhez hasonlóan a hőmérséklet- és a sókoncentráció-különbségek, a szél és az árapály hatására létrejövő [http://en.wikipedia.org/wiki/Ocean_currents tengeráramlatok] mozgását is befolyásolja. A tengeráramlásokhoz hasonlóan a folyókra is hat a Coriolis-erő: az északi féltekén a folyók erősebben alámossák a jobb partjukat. A Visegrádnál a hegyeket áttörő Duna például folyamatosan vándorol nyugatra: ezt mutatják a folyó vándorlása után visszamaradt kiskunsági homokdombok és a jobb parton végig megtalálható leszakadó löszfalak (pl. Dunaújváros, Dunaföldvár). |
| − | A | + | ===Foucault-inga=== |
| + | A Föld forgását sok kísérleti tapasztalat mutatja. A csillagászati megfigyelések mellett éppen a forgás miatt fellépő tehetetlenségi erők adják a legközvetlenebb bizonyítékokat. Történetileg leghíresebb kísérlet az 1851-ben a párizsi Panthéonban bemutatott [http://en.wikipedia.org/wiki/Foucault_pendulum Foucault-inga]. A mozgó ingára a Földhöz rögzített koordinátarendszerben hat a Coriolis-erő, és emiatt az inga lengési síkja lassan elfordul. Inerciarendszerből nézve az inga lengési síkja változatlan marad, és a Föld fordul el alatta. Az elfordulás sebessége függ a földrajzi helytől: a sarkokon egy [[Tér_és_idő#Milyen_hosszú_egy_nap?|csillag-nap]] alatt teljesen körbefordul, más helyeken viszont lassabban (az egyenlítőn pedig egyáltalán nem) fordul el. | ||
| − | + | ---- | |
| + | Vissza a [[Fizika 1i]] nyitóoldalára | ||
| − | + | 1. [[Tér és idő]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | 2. | + | 2. '''Mozgás és megjelenítése''' |
3. [[Megmaradási törvények a mechanikában]] | 3. [[Megmaradási törvények a mechanikában]] | ||
A lap 2011. február 9., 09:48-kori változata
Minden mozog körülöttünk. Vajon mi lehet a mozgások oka, milyen természettörvények írják le a mozgásokat? „Már a régi görögök is” sokat gondolkoztak ezen, mégis mintegy 2000 évnek kellett eltelnie, mire – Newton munkásságának köszönhetően – pontos választ kaphattunk ezekre a kérdésekre. Newton törvényeinek ismerete elengedhetetlen a környező világ mozgásainak megértéséhez a bolygómozgásoktól kezdve a biliárdgolyókon keresztül egészen az atomi felbontású alagútmikroszkóp piezo mozgatójáig. A mozgásegyenletek megoldásában sokat segíthet a számítógép. Ugyanakkor a számítógépes animációk is csak akkor élethűek, ha tükrözik ezeket a szabályszerűségeket.
Tartalomjegyzék[elrejtés] |
Az erő
Deformáció és mozgásállapot-változás
A hétköznapi tapasztalat alapján könnyen arra a téves megállapításra juthatunk, amit az ókori gondolkodók is vallottak, hogy egy test mozgásának a fenntartásához külső hatás szükséges: ahhoz, hogy vízszintes talajon egyenletes sebességgel biciklizzünk, folyamatosan tekerni kell, különben a bicikli előbb-utóbb megáll. A jelenség részletesebb vizsgálatával azonban rájöhetünk, hogy a biciklire rajtunk kívül más is hat (például a légellenállás vagy a gördülési ellenállás) és nekünk éppen azért kell tekernünk, hogy ezeket a hatásokat kiegyenlítsük. Ha egy testet minden más test hatásától mentesen (például a világűrben, az égitestektől távol) magára hagyunk, akkor a kezdeti sebességét megtartva egyenes vonalú egyenletes mozgással fog mozogni.
A newtoni dinamika alapvető állítása, hogy nem a mozgás fenntartásához, hanem a mozgásállapot megváltoztatásához van szükség külső hatásra. Ez a külső hatás az erő. A testet érő hatásnak a nagysága és az iránya is fontos: az erő vektoriális mennyiség.
A testre ható erő azonban nem csak a test mozgásállapotát változtatja meg, hanem a testet kisebb-nagyobb mértékben deformálja is. A test alakváltozása (deformációja) lehetőséget ad az erő egyszerű mérésére.
Erőmérés
A testre ható erő és a test deformációja között általában nagyon bonyolult a kapcsolat. Az erő méréséhez leginkább rugalmas testek aránylag kismértékű alakváltozása alkalmas. Rugalmas testet azért célszerű választani, mert az az erőhatás megszűntével újra felveszi eredeti alakját. Ezen kívül legtöbb rugalmas test deformációja a tapasztalat szerint aránylag kis alakváltozás esetén lineárisan változik az erőhatással.
Ilyen erőmérő eszköz az egyszerű rúgós erőmérő is, de a mérni kívánt erő nagyságától, a mérés pontosságától függően sokféle ilyen elven működő eszköz készíthető.
Newton III. törvénye
Az erő mindig két test közötti kölcsönhatás. Ha egy A test hat egy másik, B testre, akkor a B test is hatni fog az A testre. A tapasztalat szerint a két erő azonos nagyságú, de ellentétes irányú. Ezt a tapasztalatot fogalmazza meg Newton III. törvénye (hatás-ellenhatás törvénye):![\[\vec{F}_{\rm AB}=-\vec{F}_{\rm BA}\]](/images/math/5/6/2/5624fa47f3fc74bbd4079fb7c9c1da4d.png)
Később (a jelenségek egyszerűbb leírása érdekében) be fogunk vezetni fiktív (nem valóságos) erőket, melyek nem kölcsönhatások. Egy testre ható valódi erő esetében azonban mindig meg lehet találni azt a másik testet, amely hat rá.
Newton II. törvénye
A tehetetlen tömeg
Egy test a rá ható erő hatására megváltoztatja mozgásállapotát, azaz meg fog változni a sebessége (a sebesség nagysága, iránya vagy nagysága és iránya). A tapasztalat szerint a test gyorsulása arányos a testre ható erő nagyságával:![\[a \sim F\qquad{\rm vagy}\qquad\frac{F}{a}={\rm const.}\]](/images/math/0/c/8/0c8beb7ba8af1074b2214a9b2b23e361.png)
![\[\frac{F}{a}=m\]](/images/math/b/1/d/b1da99b83891791bc98e09ef080c0cc5.png)
![\[\vec{F}=m\vec{a}\]](/images/math/e/b/1/eb147e6dac77af812afdc10b6dd94c7b.png)
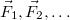 erők külön-külön
erők külön-külön 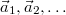 gyorsulásokat okoznának. Ha az erők egyszerre hatnak a testre, akkor a test gyorsulása ezeknek a gyorsulásoknak az összege lesz, tehát az erők egymástól függetlenül hatnak (erőhatások függetlenségének elve, szokás Newton IV. törvényének is nevezni):
gyorsulásokat okoznának. Ha az erők egyszerre hatnak a testre, akkor a test gyorsulása ezeknek a gyorsulásoknak az összege lesz, tehát az erők egymástól függetlenül hatnak (erőhatások függetlenségének elve, szokás Newton IV. törvényének is nevezni): ![\[\vec{a}=\vec{a}_1+\vec{a}_2+\dots=\frac{\vec{F}_1}{m}+\frac{\vec{F}_2}{m}+\dots=\frac{\Sigma\vec{F}}{m}\]](/images/math/e/a/2/ea254b7133082df5240f9dd7c0f21cb6.png)
A tömeg és az erő mértékegysége
A tömeg SI mértékegysége a kilogramm (kg). Ezt a mértékegységet még nem vezették vissza alapvető természeti állandókra. Eredeti meghatározása szerint 1 dm 4°C-os víz tömege, 1889 óta pedig 1 kg a kilogramm etalon (egy Párizs közelében őrzött platina-irídium henger) tömege. A mértékegység másik zavaró furcsasága, hogy az SI alapegység történeti okokból kilo- előtagot tartalmaz.
4°C-os víz tömege, 1889 óta pedig 1 kg a kilogramm etalon (egy Párizs közelében őrzött platina-irídium henger) tömege. A mértékegység másik zavaró furcsasága, hogy az SI alapegység történeti okokból kilo- előtagot tartalmaz.
Az erő SI mértékegysége a newton (N). 1 N az az erő, ami egy 1 kg tömegű testet 1 m/s gyorsulással gyorsít. Az erő régebbi mértékegysége a kilopond (kp) volt, ami egy 1 kg tömegű test súlya (a 45° szélességen, tengerszinten).
gyorsulással gyorsít. Az erő régebbi mértékegysége a kilopond (kp) volt, ami egy 1 kg tömegű test súlya (a 45° szélességen, tengerszinten).
Mechanikai erőhatások
Nehézségi erő
A Földön minden testre hat a nehézségi erő, ami lényegében a Föld gravitációs vonzásából származik (de attól kicsit eltér a Föld forgása miatt). A nehézségi erő un. térfogati erő: a kiterjedt test minden pontjára hat. Feladatok megoldásánál azonban a testre ható nehézségi erőt egyetlen, a tömegközéppontban ható erővel vesszük figyelembe. A nehézségi erő arányos a test tömegével: 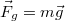 , ahol
, ahol 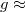 9,81 m/s
9,81 m/s , a Föld felszínének közelében csak kis mértékben változó nagyságú nehézségi gyorsulás. A nehézségi erő iránya definíciószerűen a függőleges irány (ami a forgás miatt nem pontosan a Föld középpontja felé mutat).
, a Föld felszínének közelében csak kis mértékben változó nagyságú nehézségi gyorsulás. A nehézségi erő iránya definíciószerűen a függőleges irány (ami a forgás miatt nem pontosan a Föld középpontja felé mutat).
Kényszererők
A testek mozgásuk során nem mozoghatnak szabadon: más testek kényszerfeltételeket szabhatnak a test mozgására. Ezek a kényszerek is erők formájában hatnak a testre, ezeket a különböző erőket nevezzük kényszererőknek.
Kiterjedt testek nem hatolhatnak akadálytalanul egymásba, ezért egy másik (merev) test felülete kényszerként megakadályozza a test szabad mozgását. A két test felülete közt ható erő a nyomóerő ( ). A nyomóerő mindig merőleges a felületre, nagyságát azonban a testre ható más erők és a test mozgása határozza meg.
). A nyomóerő mindig merőleges a felületre, nagyságát azonban a testre ható más erők és a test mozgása határozza meg.
Egy másik, gyakran előforduló kényszererő a fonálerő (kötélerő). Egy fonálra rögzített test mozgását korlátozza a fonál: a testre a többi erő és a test mozgásától függő nagyságú fonálirányú húzó erő hat.
Súrlódás, közegellenállás
Két test érintkezésekor a felületre merőleges nyomóerőn kívül a felülettel párhuzamos erő is felléphet, ez a súrlódási erő (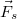 ). Megkülönböztetünk nyugalmi (tapadási) és mozgási (csúszási) súrlódást.
). Megkülönböztetünk nyugalmi (tapadási) és mozgási (csúszási) súrlódást.
A tapadási súrlódási erő két egymáshoz képest álló felület közt lép fel. Nagysága és iránya mindig olyan, hogy akadályozza a testek egymáshoz képesti elmozdulását. Nagysága azonban nem lehet tetszőlegesen nagy: 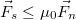 , ahol
, ahol 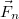 a felületen ható nyomóerő,
a felületen ható nyomóerő, 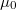 pedig a felületek anyagától és minőségétől függő tapadási súrlódási együttható.
pedig a felületek anyagától és minőségétől függő tapadási súrlódási együttható.
A csúszási súrlódási erő két egymáshoz képest mozgó felület között hat. Iránya mindig a relatív elmozdulással ellentétes irányú. Nagysága arányos a felületek közt ható nyomóerővel: 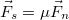 , ahol
, ahol  a (szintén a felületek anyagától és minőségétől függő) csúszási súrlódási együttható. Általában
a (szintén a felületek anyagától és minőségétől függő) csúszási súrlódási együttható. Általában 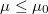 .
.
A levegőben (gázokban) vagy folyadékban mozgó testekre ható fékező erő a közegellenállás (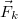 ). Kis sebességeknél a fékező erőt a gáz (folyadék) és a test közti viszkózus súrlódás okozza, ilyenkor
). Kis sebességeknél a fékező erőt a gáz (folyadék) és a test közti viszkózus súrlódás okozza, ilyenkor 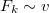 . Nagyobb sebességeknél viszont a mozgó test mögött kialakuló örvények fékezik a testet, ekkor
. Nagyobb sebességeknél viszont a mozgó test mögött kialakuló örvények fékezik a testet, ekkor 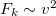 . A légellenállás vizsgálatára egy konkrét feladat kapcsán visszatérünk.
. A légellenállás vizsgálatára egy konkrét feladat kapcsán visszatérünk.
A relatív sebességgel ellentétes irányú fékező erőn kívül felléphetnek oldalirányú erők is, például a repülésben alapvetően fontos aerodinamikai felhajtóerő, vagy a forgó tárgyaknál fellépő Magnus-hatás.
Newton II. törvénye a nanotechnológiában
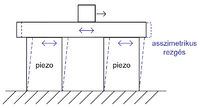
A tehetetlenségi piezo mozgató
Látványos kísérlet, amit egy kis gyakorlással bárki megcsinálhat: úgy lehet kirántani egy abroszt a teríték alól, hogy a poharak, tányérok éppen csak megmozdulnak.
A kísérlet alapja a testek tehetetlensége. Ha egy vízszintes tálcára poharakat állítunk, és a tálcát lassan (kis gyorsulással) mozgatni kezdjük, akkor a tapadási súrlódás miatt a poharak a tálcával együtt fognak mozogni. Ha viszont a tálcát hirtelen (nagy gyorsulással) mozgatjuk, akkor a poharak megcsúsznak, és tehetetlenségük miatt nem követik a tálca mozgását. Ha a tálcát kis kitéréssel, de aszimmetrikusan, az egyik irányban kis gyorsulással, a másik irányba nagy gyorsulással mozgatjuk, akkor elérhetjük, hogy a poharak a tálcán lassan vándoroljanak: egyik irányban a tálcával együtt mindig elmozdulnak egy kicsit, a másik irányban viszont megcsúsznak, és lényegében helyben maradnak.
Ilyen elven működnek a gyárakban anyagok mozgatására használt rázócsúszdák (ahol megfelelő rezgetéssel akár gyengén felfelé is csúszhatnak a tárgyak), és ugyanezen az elven alapul a tehetetlenségi piezo mozgató, amivel apró tárgyakat akár több cm távolságra el lehet juttatni atomi (tized nm) pontossággal.
A piezo kristályok a kristálylapokra kapcsolt feszültség hatására deformálódnak (deformáció hatására pedig feszültség keletkezik rajtuk). A feszültség finom szabályozásával a kristály szabad vége akár tized nm-es pontossággal mozgatható. Az ilyen elven működő különböző pásztázó mikroszkópok segítségével egy anyag felülete atomi felbontással letapogatható.
A piezo kristály szabad vége azonban csak kis elmozdulásokra képes. Nagyobb (cm-es) távolságokra úgy lehet eljuttatni egy apró tárgyat, hogy a kristályra aszimmetrikus (fűrészfog alakú) feszültségjelet kapcsolnak. Így a tárgy az egyik irányban (kis gyorsulással) a súrlódás miatt a kristály végével együtt mozog, a másik irányban viszont megcsúszik a nagy gyorsulással mozgó kristályon, és lényegében helyben marad. Így a kristály (aszimmetrikus) rezgése hatására apró lépésekben egy irányba halad.
Valóságos mozgások modellezése
Milyen hatásokat fontos figyelembe venni?
Feladatgyűjteményekben gyakran olvasható egy-egy feladat végén, hogy valamilyen hatás (pl. a súrlódás vagy a légellenállás) „elhanyagolható”.
A valóságban azonban egy fizikai folyamatot végtelen sok hatás befolyásol kisebb-nagyobb mértékben. (A hőmérséklet- és nyomásváltozásoktól az elektromos és mágneses hatásokon keresztül távoli testek gravitációs hatásáig.) Egy valódi probléma esetében ezért célszerűbb azt vizsgálni, hogy mi az a néhány hatás, amit a megoldáshoz mindenképp figyelembe kell venni. A súrlódás vagy a légellenállás nagyon sok mozgás esetében meghatározó, és a helyes megoldás érdekében annak ellenére figyelembe kell venni, hogy a megoldást bonyolultabbá teszi. (Mint látni fogjuk a numerikus módszereknek köszönhetően így sem válnak a feladatok megoldhatatlanná.)
Egy-egy konkrét feladat esetében nem mindig könnyű eldönteni, hogy melyek azok a hatások, amelyek semmiképp nem elhanyagolhatók. Ebben egyrészt a gyakorlat, másrészt – szükség esetén – próbaszámítások vagy kísérletek segíthetnek.
Példaképp vizsgáljuk egy kanyarban haladó autó mozgását. Az egyenletes sebességgel haladó járműnek valamilyen okból hirtelen fékeznie kell. Legfeljebb mekkora lehet a fékezés megkezdésekor a lassulása? Ha állandó erővel fékez, mekkora úton áll meg? Hogyan változik a kerekekre ható súrlódási erő az idő függvényében?
Milyen hatásokat kell figyelembe venni? A járműre hat a nehézségi erő és a talaj nyomóereje. Az út és a kerekek közti tapadási súrlódás semmiképp nem elhanyagolható, hiszen nélküle se kanyarodni, se fékezni nem lehet. Ennek a problémának a megoldásánál ezeket az erőkkel számolunk.
A légellenállás általában szintén nem elhanyagolható hatás egy jármű mozgására (hiszen vízszintes úton nagyobb sebességeknél elsősorban emiatt kell egyenletes sebességgel való haladáshoz is nyomni a gázpedált), de a hirtelen fékezéskor fellépő nagy erők mellett ebben az esetben szerepe másodlagos. (Ráadásul nincs információnk a szélről, ami a légellenállást szintén erősen befolyásolja.)
A mozgásegyenletek felírása
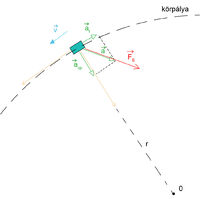
A mozgásegyenlet felírásához érdemes vázlatot készíteni a testre ható erőkről, ahol a test sebességét, gyorsulását, és a választott koordinátarendszer tengelyeit is feltüntetjük.
A mi esetünkben a rajzon a vízszintes erőket és irányokat rajzoljuk be (2. ábra), ezen kívül a testre függőleges irányban lefelé az 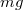 nehézségi erő, felfelé pedig az
nehézségi erő, felfelé pedig az 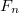 nyomóerő hat. Vízszintes irányban csak a talaj és a kerekek közt fellépő
nyomóerő hat. Vízszintes irányban csak a talaj és a kerekek közt fellépő 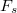 tapadási súrlódási erő hat. A koordinátatengelyeket a jármű haladási irányában előre és erre merőlegesen, a kör középpontja irányában vesszük fel. A test a kanyarodás miatt gyorsul a kör középpontja felé (
tapadási súrlódási erő hat. A koordinátatengelyeket a jármű haladási irányában előre és erre merőlegesen, a kör középpontja irányában vesszük fel. A test a kanyarodás miatt gyorsul a kör középpontja felé (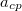 centripetális gyorsulás) és a fékezés miatt a pálya érintőjének irányában is (
centripetális gyorsulás) és a fékezés miatt a pálya érintőjének irányában is (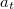 tangenciális gyorsulás).
tangenciális gyorsulás).
![\[F_n-mg=0\]](/images/math/9/8/e/98e8023aab930aae7e989c3596165a3f.png)
![\[\vec{a}=\vec{a}_{cp}+\vec{a}_t\]](/images/math/d/0/1/d01f505717999fffaeb92e10a48fc478.png)
![\[a=\sqrt{a_{cp}^2+a_t^2}\]](/images/math/9/a/b/9ab7c9862f4cb35ddb48a7ce84ba40de.png)
![\[a_{cp}=\frac{v^2}{r}\]](/images/math/2/8/3/283e2c2073ab602a16535abfe47bcf7d.png)
 a pálya sugara. Vízszintes irányban csak a súrlódási erő hat, így Newton II. törvénye alapján:
a pálya sugara. Vízszintes irányban csak a súrlódási erő hat, így Newton II. törvénye alapján: ![\[F_s=ma\]](/images/math/c/b/1/cb17df9414789d70e7566dce79047c09.png)
![\[F_s\leq\mu F_n\]](/images/math/a/a/d/aad49844b4d01aa089dbc7887e424c72.png)
Ezeket az egyenleteket és egyenlőtlenségeket kell megoldanunk.
Kezdeti feltételek megadása
A probléma egyértelmű megoldásához a mozgásegyenleteken kívül szükség van a kezdeti feltételek megadására. Ugyanolyan mozgásegyenleteknek egész más megoldása lehet, ha mások a kezdeti feltételek. Például, ha a testre csak a nehézségi erő hat (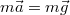 ,
, 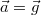 ), akkor a kezdeti feltételektől függően lehet a mozgás szabadesés (
), akkor a kezdeti feltételektől függően lehet a mozgás szabadesés (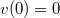 ), függőleges, vízszintes vagy ferde hajítás is.
), függőleges, vízszintes vagy ferde hajítás is.
Esetünkben a kezdeti sebesség (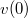 ) értékére van szükségünk. (Látni fogjuk, hogy ettől függően lehet, vagy nem lehet fékezni.)
) értékére van szükségünk. (Látni fogjuk, hogy ettől függően lehet, vagy nem lehet fékezni.)
A mozgásegyenlet megoldása
Az egyenletrendszer könnyen megoldható:![\[F_n=mg\]](/images/math/3/d/9/3d98e668ed07a90b835b6cc4223baae8.png)
![\[ma=F_s\leq\mu F_n=\mu mg\]](/images/math/2/d/4/2d4b071abe90171116d550a4759c74f2.png)
![\[a\leq\mu g\]](/images/math/2/1/e/21ee9b8e2db960ac889f4c57d5a3c1e9.png)
![\[\left|a_t\right|=\sqrt{a^2-a_{cp}^2}\leq\sqrt{(\mu g)^2-\frac{v^4}{r^2}}\]](/images/math/3/e/4/3e4cde8a27e6c7ea050e6025f8880134.png)
![\[|a_t|_{max}=\sqrt{(\mu g)^2-\frac{\left[v(0)\right]^4}{r^2}}\]](/images/math/4/5/2/452cd33738db7c8cea4073a2d039617f.png)
![\[\mu g\geq\frac{\left[v(0)\right]^2}{r}\]](/images/math/c/b/c/cbcacca0760320ccb1b3928adc7210b8.png)
![\[v\leq\sqrt{\mu rg}\]](/images/math/9/e/0/9e0ec7068c94c6119cb215b9a07d38bf.png)
Ha 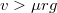 , akkor a jármű már a fékezés előtt, kanyarodás közben megcsúszik, ha
, akkor a jármű már a fékezés előtt, kanyarodás közben megcsúszik, ha 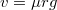 akkor a kanyart még éppen be lehet venni, de fékezni már egyáltalán nem lehet.
akkor a kanyart még éppen be lehet venni, de fékezni már egyáltalán nem lehet.
![\[v(t)=v(0)+a_t t=v(0)-\left|a_t\right|_{max}t\]](/images/math/6/3/a/63a1fd1926310b9a54387f1c653a08cd.png)
![\[v(t)=0\quad\Leftrightarrow\quad t=\frac{v(0)}{\left|a_t\right|_{max}}\]](/images/math/0/5/2/05287fe1a9a641fd722ff2c9b4cf482f.png)
![\[s=v(0)t-\frac{1}{2}\left|a_t\right|_{max}t^2=\frac{\left[v(0)\right]^2}{2\left|a_t\right|_{max}}\]](/images/math/8/a/7/8a773ec617b3975d67d3d7a0388410b7.png)
(A fékerő fokozatos változtatásával a fékút lehet rövidebb: a sebesség csökkenésével csökken a centripetális gyorsulás, és így egyre nagyobb lehet a jármű lassulása.)
A súrlódási erő időfüggése:![\[F_s=ma=m\sqrt{a_{cp}^2+a_t^2}=m\sqrt{\frac{\left[v(t)\right]^4}{r^2}+|a_t|_{max}^2}\]](/images/math/5/c/b/5cb435e9b492bbbc2371853d7974a2c9.png)
A megoldás ábrázolása grafikonokkal
A megoldás grafikonokkal (elmozdulás-idő, sebesség-idő, sebesség-elmozdulás, stb.) vagy animációval tehető szemléletessé.
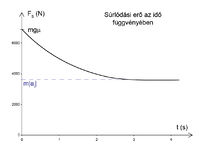
A 3. ábra a fékút függését ábrázolja a  (0) sebességtől (adatok:
(0) sebességtől (adatok:  = 0,7,
= 0,7,  = 40 m). A 4. ábrán a súrlódási erő időfüggése látható (adatok:
= 40 m). A 4. ábrán a súrlódási erő időfüggése látható (adatok:  (0) = 55 km/h,
(0) = 55 km/h,  = 1000 kg).
= 1000 kg).
Szabadesés légellenállással
A feladat megoldása egyszerű numerikus módszerekkel
A Földön a szabadon eső testekre a nehézségi erőn kívül (különleges, vákuumban végzett kísérletektől eltekintve) a levegő közegellenállása is hat. A tapasztalat szerint a közegellenállási erő a sebesség növekedésével egyre nagyobb lesz, a test egyre kisebb gyorsulással gyorsul, míg végül – elegendően hosszú esési idő után – állandósult sebességgel, egyenes vonalú egyenletes mozgással esik tovább. Az, hogy a testre ható közegellenállási erő mennyi idő után válik meghatározó hatássá, függ az eső test méretétől, sűrűségétől és alakjától, valamint a közeg (a levegő vagy esetleg más gáz, folyadék) tulajdonságaitól is. Például egy porszem vagy egy ejtőernyős már viszonylag hamar egyenletes sebességgel esik, egy nagyobb kő viszont aránylag sokáig gyorsul.
Az eső testre a nehézségi erő és a közegellenállás hat, a mozgásegyenlet könnyen felírható. (A mozgás egyenes vonalú, így nincs szükség vektoregyenletre. A pozitív irányt függőlegesen lefelé választottuk.)![\[ma=mg-F_k\]](/images/math/d/6/3/d63ba27f01cac3546f9f9f6cf27eb167.png)
Az 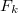 közegellenállási erő nagysága függ a test méretétől, alakjától, sebességétől, valamint a közeg tulajdonságaitól is. Aránylag kis sebességeknél a testre ható fékező erőt a közeg viszkozitása (belső súrlódása) okozza. Ilyen eset például egy apró porszem esése levegőben, vagy egy kanál süllyedése mézben Ekkor az erő a test sebességével arányos, gömb alakú test estében például
közegellenállási erő nagysága függ a test méretétől, alakjától, sebességétől, valamint a közeg tulajdonságaitól is. Aránylag kis sebességeknél a testre ható fékező erőt a közeg viszkozitása (belső súrlódása) okozza. Ilyen eset például egy apró porszem esése levegőben, vagy egy kanál süllyedése mézben Ekkor az erő a test sebességével arányos, gömb alakú test estében például 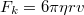 , ahol
, ahol  a gömb sugara,
a gömb sugara,  pedig a közeg viszkozitása (Stokes-törvény).
pedig a közeg viszkozitása (Stokes-törvény).
![\[F_k=\frac{1}{2}\rho v^2cA\]](/images/math/b/8/1/b81624683057adbed0d52a7986639be5.png)
 a közeg sűrűsége,
a közeg sűrűsége,  a test keresztmetszete,
a test keresztmetszete,  pedig a dimenziótlan formatényező.
Ha az utóbbi modellt használjuk, és a közegellenállási erőt röviden
pedig a dimenziótlan formatényező.
Ha az utóbbi modellt használjuk, és a közegellenállási erőt röviden 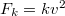 alakban írjuk (ahol
alakban írjuk (ahol  egy állandó, amely csak a test méretétől és alakjától, valamint a közeg sűrűségétől függ), akkor a mozgásegyenlet:
egy állandó, amely csak a test méretétől és alakjától, valamint a közeg sűrűségétől függ), akkor a mozgásegyenlet: ![\[ma=mg-kv^2\]](/images/math/a/d/f/adfd31cb1f7653325633a0279cef9bfe.png)
 és
és  nem ismeretlen (időben állandó) mennyiségek, hanem ismeretlen függvények:
nem ismeretlen (időben állandó) mennyiségek, hanem ismeretlen függvények:  és
és 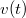 . A mozgásegyenlet, amit felírtunk, egy függvényegyenlet:
. A mozgásegyenlet, amit felírtunk, egy függvényegyenlet: ![\[ma(t)=mg-k\left[v(t)\right]^2\]](/images/math/6/4/c/64c03f82be1584e8f1ee26efdd11a098.png)
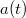 és
és 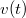 azonban nem függetlenek egymástól:
azonban nem függetlenek egymástól: ![\[a(t)=\frac{{\rm d}v(t)}{{\rm d}t}\]](/images/math/0/a/e/0ae1537842e49b0641768d46b31cafaa.png)
![\[\frac{{\rm d}v(t)}{{\rm d}t}=g-\frac{k}{m}\left[v(t)\right]^2\]](/images/math/e/1/f/e1f5ee636ffd9f524ef6f44d7d2dd523.png)
Differenciálegyenletek numerikus megoldására nagyon sok módszer van, itt most egy nagyon egyszerű, fizikai szempontból szemléletes megoldást mutatunk be.
Ha ismerjük a test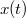 helyét és
helyét és 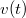 sebességét egy
sebességét egy  időpontban, akkor a mozgásegyenlet alapján ki tudjuk számítani a gyorsulását is:
időpontban, akkor a mozgásegyenlet alapján ki tudjuk számítani a gyorsulását is: ![\[a(t)=g-\frac{k}{m}\left[v(t)\right]^2\]](/images/math/b/0/a/b0a15c8a7190455dd598863df8ad1a7c.png)
 időtartam alatt keveset változik, ezért a test sebességét és helyét a
időtartam alatt keveset változik, ezért a test sebességét és helyét a 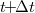 időpontban jó közelítéssel ki tudjuk számolni úgy, mintha egyenletesen gyorsuló mozgás lenne:
időpontban jó közelítéssel ki tudjuk számolni úgy, mintha egyenletesen gyorsuló mozgás lenne: ![\[v(t\!\!+\!\!\Delta t)\approx v(t)+a(t)\Delta t\]](/images/math/e/d/8/ed8faf5cdaec06d3aa02014704dcb1d3.png)
![\[x(t\!\!+\!\!\Delta t)\approx x(t)+v(t)\Delta t+\frac{1}{2}a(t)(\Delta t)^2\]](/images/math/7/2/a/72ab4013c873b836b9665f8af26be1fe.png)
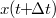 és
és 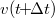 ismeretében már meghatározható
ismeretében már meghatározható 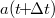 , és az eljárás megismételhető.
, és az eljárás megismételhető.
A számítás elvégzéséhez szükség van a kezdeti feltételek (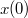 és
és 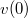 ), valamint a befejezés feltételének megadására (például a vizsgált időtartam, vagy a földetérés távolságának a megadására). Ezen kívül meg kell választani
), valamint a befejezés feltételének megadására (például a vizsgált időtartam, vagy a földetérés távolságának a megadására). Ezen kívül meg kell választani  értékét. Túl nagy
értékét. Túl nagy  választása esetén a számítás pontatlan, túl kicsi érték viszont feleslegesen hosszú számítási időt eredményez.
választása esetén a számítás pontatlan, túl kicsi érték viszont feleslegesen hosszú számítási időt eredményez.
A számítás az algoritmus alapján bármely programnyelvvel (akár excel táblázatkezelővel is) elvégezhető, a mozgás grafikonokkal vagy animációval szemléltethető.
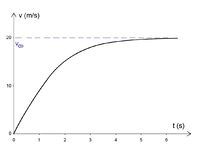
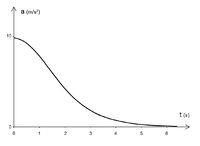
Az 5. és 6. ábrán látható grafikonok egy 100 m magasról leeső focilabda sebességét és gyorsulását ábrázolják az idő föggvényében (adatok: = 0,435 kg,
= 0,435 kg,  = 0,22 m,
= 0,22 m,  = 1,2 kg/m
= 1,2 kg/m , c = 0,47). Jól látható, hogy a gyorsulás a kezdeti
, c = 0,47). Jól látható, hogy a gyorsulás a kezdeti 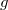 értékről indulva nullához, a sebesség pedig egy határértékhez (az állandósult sebességhez) tart. A határsebesség a mozgásegyenletből kifejezhető:
értékről indulva nullához, a sebesség pedig egy határértékhez (az állandósult sebességhez) tart. A határsebesség a mozgásegyenletből kifejezhető: ![\[v_\infty=\sqrt{\frac{mg}{k}}\]](/images/math/7/9/e/79efaec8513868aa4ce0e2cdee353449.png)
Az adatokat behelyettesítve ez esetünkben kb. 20 m/s (72 km/h).
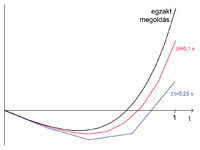
A numerikus megoldás veszélyei
A numerikus megoldás minden lépése közelítő, a kicsiny hibák idővel felhalmozódnak, a számítás eredménye egyre távolabb kerülhet az egzakt megoldás eredményétől. Kaotikus rendszerek különösen érzékenyek erre. A lépésköz csökkentésével a hiba csökkenthető (7. ábra) – ez viszont bonyolultabb számításoknál a program futási idejét növelheti meg túlságosan.
Bizonyos esetekben lehetőség van a felhalmozódó hibák részleges kijavítására is. Például ha a rendszerben a teljes mechanikai energia állandó, akkor ezt a feltételt is figyelembe lehet venni a számításban, és ezzel el lehet kerülni, hogy a numerikus megoldásban az összenergia folyamatosan növekedjen vagy csökkenjen.
Newton gravitációs törvénye
A törvény „ellenőrzése”
Newton nevéhez kötődik a róla elnevezett törvényeken kívül a gravitációs kölcsönhatás leírása is. Az általános tömegvonzás törvényének megalkotásához Newtont két fontos tapasztalat segítette: Galilei kísérletekkel igazolt állítása, miszerint a szabadon eső testek gyorsulása (ha a légellenállást elhanyagolható) nem függ a testek tömegétől, és Kepler III. törvénye, amely az égitestek keringési ideje és a pályájuk fél nagytengelye között teremt kapcsolatot.
Ezekből a tapasztalatokból, figyelembe véve Newton II. törvényét következik, hogy a tömegvonzás egyenesen arányos a kölcsönhatásban résztvevő testek tömegével és fordítva arányos a testek távolságának négyzetével. Így a gravitációs erő nagysága![\[F_g=\gamma\frac{m_1 m_2}{r^2}\]](/images/math/9/5/b/95bce6de2414ea671bf69665bb6aff68.png)
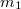 és
és 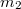 a testek tömege,
a testek tömege, a két tömegpont távolsága (kiterjedt testeknél, ha a testek gömbszimmetrikusak, a gömbök középpontjának távolsága),
a két tömegpont távolsága (kiterjedt testeknél, ha a testek gömbszimmetrikusak, a gömbök középpontjának távolsága),  pedig egy egyelőre ismeretlen állandó. Az erő mindig vonzóerő, iránya a két testet összekötő egyenes.
pedig egy egyelőre ismeretlen állandó. Az erő mindig vonzóerő, iránya a két testet összekötő egyenes.
Newton a törvény ellenőrzésére a Föld felszínének közelében szabadon eső test és a Föld körül első közelítésben körpályán keringő Hold mozgását hasonlította össze. Végezzük el mi is ezt az ellenőrzést!
A szabadon eső testre (elhanyagolva a légellenállást) csak a Föld gravitációs ereje hat:![\[F=\gamma\frac{m m_F}{r_F^2}\]](/images/math/e/6/f/e6ff8340c7dc3523da242b7a01f3124d.png)
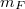 a Föld tömege,
a Föld tömege, 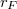 pedig a Föld sugara (hiszen a Föld felszínén lévő test ilyen távolságra van a Föld középpontjától). A testre felírt mozgásegyenlet (elhanyagolva, hogy a Föld forog):
pedig a Föld sugara (hiszen a Föld felszínén lévő test ilyen távolságra van a Föld középpontjától). A testre felírt mozgásegyenlet (elhanyagolva, hogy a Föld forog): ![\[F=mg\]](/images/math/9/f/8/9f80400fd8b69c167d015047fc94bd64.png)
![\[\gamma\frac{m m_F}{r_F^2}=mg\]](/images/math/b/e/4/be4b084a1aa9f9054646779be1e0ee26.png)
![\[\gamma m_F=g r_F^2\]](/images/math/e/2/9/e296c1c74f5d0b0055d5cfcfcdbb16ad.png)
![\[F_H=\gamma\frac{m_H m_F}{r_H^2}\]](/images/math/7/5/0/750bff8c74a2f10ee92003fd5e7f861c.png)
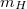 a Hold tömege,
a Hold tömege, 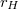 pedig a Föld-Hold távolság (a középpontjaik közti távolság). A Hold első közelítésben körpályán mozog a Föld körül, így a mozgásegyenlet:
pedig a Föld-Hold távolság (a középpontjaik közti távolság). A Hold első közelítésben körpályán mozog a Föld körül, így a mozgásegyenlet: ![\[F_H=m_H a_cp\]](/images/math/c/5/8/c58eb7ebf130addb43595be34592d356.png)
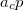 a Hold centripetális gyorsulása. A két egyenletből
a Hold centripetális gyorsulása. A két egyenletből ![\[\gamma\frac{m_H m_F}{r_H^2}=m_H a_cp\]](/images/math/4/3/4/43452bac561ace4086962d01c2d884b0.png)
![\[\gamma m_F=a_cp r_H^2\]](/images/math/2/1/e/21e1b870658bc37987ddcdec60adbe10.png)
![\[a_cp=r_H \omega_H^2=r_H\frac{4\pi^2}{T_H^2}\]](/images/math/f/0/0/f0098e11c65c0b8d61652a0d05b14d92.png)
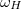 a Hold keringésének szögsebessége,
a Hold keringésének szögsebessége,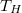 pedig a Hold keringési ideje. Ezt behelyettesítve
pedig a Hold keringési ideje. Ezt behelyettesítve ![\[\gamma m_F=\frac{4\pi^2}{T_H^2}r_H^3\]](/images/math/e/9/6/e96547977d223e7d507ffe36a9eabb3a.png)
A képletekben szereplő 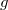 ,
, 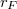 ,
, 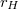 és
és 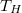 értékeket már Newton is ismerhette. A Föld-Hold távolságot a Föld sugarához hasonlóan már az ókorban megmérték parallaxis módszerrel (a Hold a Föld különböző pontjairól más irányban látszik), közepes értéke a Föld sugarának kb. 60-szorosa. A Hold keringési ideje, az un. sziderikus hónap, az az idő, ami alatt a Hold az állócsillagokhoz képest egyszer megkerüli a Földet. (Ez az idő – 27,32 nap – eltér a két azonos holdfázis, pl. két telihold közti szinodikus hónaptól – 29,53 nap –, hiszen miközben a Hold megkerüli a Földet, a Föld is elmozdul a Nap körül.)
értékeket már Newton is ismerhette. A Föld-Hold távolságot a Föld sugarához hasonlóan már az ókorban megmérték parallaxis módszerrel (a Hold a Föld különböző pontjairól más irányban látszik), közepes értéke a Föld sugarának kb. 60-szorosa. A Hold keringési ideje, az un. sziderikus hónap, az az idő, ami alatt a Hold az állócsillagokhoz képest egyszer megkerüli a Földet. (Ez az idő – 27,32 nap – eltér a két azonos holdfázis, pl. két telihold közti szinodikus hónaptól – 29,53 nap –, hiszen miközben a Hold megkerüli a Földet, a Föld is elmozdul a Nap körül.)
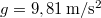 , az
, az 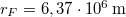 , az
, az 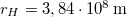 és a
és a 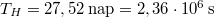 értékeket
értékeket 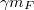 két kifejezésébe. a
két kifejezésébe. a ![\[\gamma m_F=g r_F^2=3,98\cdot 10^{14}\,{\rm m^3/s^2}\]](/images/math/8/1/2/812565d87906994e484e75230224c94d.png)
![\[\gamma m_F=\frac{4\pi^2}{T_H^2}r_H^3=4.01\cdot 10^{14}\,{\rm m^3/s^2}\]](/images/math/5/9/7/597e16254d44f7cda34e7c5b9b33ac57.png)
Súly és súlytalanság
A súly és a tömeg fogalma a hétköznapi szóhasználatban gyakran keveredik, egymás szinonimájaként használják. Pedig a két fogalom között (azon kívül, hogy a súly egy erő, tehát mértékegységét tekintve is különbözik a tömegtől) jelentős különbségek vannak. A test súlya a tömegén kívül függ a test helyétől és mozgásállapotától is.
A súly meghatározása a nemzetközi irodalomban nem egységes. A Magyarországon szokásos meghatározás szerint egy test súlya az az erő, amelyet a test az alátámasztására vagy a felfüggesztésére kifejt. Azt, hogy egy testnek súlya van, a rá ható gravitációs erő okozza, így az függ a test helyén mérhető nehézségi gyorsulástól. Ezért lesz egy test súlya kisebb a Holdon, mint a Földön (körülbelül egy hatoda a földi súlyának). A test súlya azonban csak akkor egyezik meg a rá ható gravitációs erővel, ha a test nyugalomban van (vagy egyenes vonalú egyenletes mozgást végez). Ha a test gyorsul, akkor a rá ható erők eredője nem nulla, és a test súlya különbözni fog a gravitációs erőtől.
Egyszerű méréseket lehet végezni egy liftben. Ha a nyugalomban lévő (vagy egyenletesen haladó) liftben ráállunk egy fürdőszobamérlegre, akkor az az „igazi”, nyugalmi súlyunkat fogja mutatni, 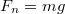 . Ha viszont a lift felfelé gyorsuló mozgást végez (felfelé gyorsít, vagy lefelé fékez), akkor a testünket a mérleg által kifejtett nyomóerő és a gravitációs erő különbsége fogja gyorsítani (
. Ha viszont a lift felfelé gyorsuló mozgást végez (felfelé gyorsít, vagy lefelé fékez), akkor a testünket a mérleg által kifejtett nyomóerő és a gravitációs erő különbsége fogja gyorsítani (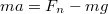 ), tehát a súlyunk (az az erő, amit a testünk kifejt az alátámasztásra – az alátámasztás által kifejtett nyomóerő ellenereje) nagyobb lesz a nyugalomban mért súlynál:
), tehát a súlyunk (az az erő, amit a testünk kifejt az alátámasztásra – az alátámasztás által kifejtett nyomóerő ellenereje) nagyobb lesz a nyugalomban mért súlynál: 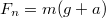 . Ehhez hasonlóan lefelé gyorsuló liftben (ha a lift lefelé gyorsít, vagy felfelé fékez) a súlyunk kisebb lesz:
. Ehhez hasonlóan lefelé gyorsuló liftben (ha a lift lefelé gyorsít, vagy felfelé fékez) a súlyunk kisebb lesz: 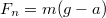 .
.
Ha egy test szabadon esik, vagy más olyan mozgást végez, ahol a gravitáción kívül nem hat rá más erő (például kering a Föld körül), akkor a súlya nulla lesz. Ez a súlytalanság állapota. Természetesen a gravitáció a súlytalanság állapotában is hat a testre: a Föld körül keringő testet például éppen a gravitáció tartja körpályán (a gravitációs erő okozza a test centripetális gyorsulását).
Mekkora a Föld tömege? A gravitációs állandó mérése
Mekkora a Föld tömege? Ha tudnánk, akkor abból a  gravitációs állandót is ki lehetne számítani, hiszen korábban kiszámítottuk a két mennyiség szorzatát. A Föld tömegét azonban nem tudjuk másképp meghatározni, csak éppen a gravitációs hatásán keresztül. Így először a
gravitációs állandót is ki lehetne számítani, hiszen korábban kiszámítottuk a két mennyiség szorzatát. A Föld tömegét azonban nem tudjuk másképp meghatározni, csak éppen a gravitációs hatásán keresztül. Így először a  állandót kell valahogy megmérni, és a Föld tömegét majd az alapján meghatározni. (A gravitációs állandó meghatározásához hasonlóan alkalmatlan a bolygók Nap körüli keringésének vizsgálata, hiszen a Nap tömegét se ismerjük független mérésből.)
állandót kell valahogy megmérni, és a Föld tömegét majd az alapján meghatározni. (A gravitációs állandó meghatározásához hasonlóan alkalmatlan a bolygók Nap körüli keringésének vizsgálata, hiszen a Nap tömegét se ismerjük független mérésből.)
A  gravitációs állandó értékét két ismert tömegű és ismert távolságú test közt fellépő erőhatás alapján lehet megmérni. Mivel hétköznapi méretű testek között ez az erőhatás más erőkhöz képest nagyon kicsi, a mérés elvégzése nem könnyű. A XVIII. század legvégén elvégzett Cavendish-kísérlet lényege, hogy a kicsiny erőt egy torziós szál elcsavarodásából lehet meghatározni. Cavendish egy vízszintes rúd végeire két egyforma, néhány kg tömegű ólomgolyót rögzített, a rudat pedig egy vékony, rugalmas szálra függesztette (torziós inga). A felfüggesztett testek mellé helyezett másik két ólomgömb vonzásának hatására a szál kis mértékben elcsavarodott, amiből a szál torziós együtthatójának és a mérés geometriai elrendezésének ismeretében a fellépő gravitációs erő és a gravitációs állandó értéke kiszámítható:
gravitációs állandó értékét két ismert tömegű és ismert távolságú test közt fellépő erőhatás alapján lehet megmérni. Mivel hétköznapi méretű testek között ez az erőhatás más erőkhöz képest nagyon kicsi, a mérés elvégzése nem könnyű. A XVIII. század legvégén elvégzett Cavendish-kísérlet lényege, hogy a kicsiny erőt egy torziós szál elcsavarodásából lehet meghatározni. Cavendish egy vízszintes rúd végeire két egyforma, néhány kg tömegű ólomgolyót rögzített, a rudat pedig egy vékony, rugalmas szálra függesztette (torziós inga). A felfüggesztett testek mellé helyezett másik két ólomgömb vonzásának hatására a szál kis mértékben elcsavarodott, amiből a szál torziós együtthatójának és a mérés geometriai elrendezésének ismeretében a fellépő gravitációs erő és a gravitációs állandó értéke kiszámítható: 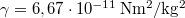 .
.
![\[m_F=\frac{g r_F^2}{\gamma}=5,97\cdot10^{24}\,{\rm kg}\]](/images/math/0/9/4/09415444dc774bfd63889311b9c56d9b.png)
![\[\rho_F=\frac{m_F}{V_F}=5510\,{\rm kg/m^3}\]](/images/math/a/0/2/a02afd3fb59641a0bd21155e4b8ab029.png)
A gravitációs állandó ismeretében a Föld (vagy más bolygók) pályaadataiból ehhez hasonlóan meghatározható a Nap tömege és sűrűsége is.
Newton I. törvénye
Az inerciarendszer fogalma
Newton I. törvénye kimondja, hogy ha egy testre nem hat erő, vagy a rá ható erők eredője 0, akkor a test nyugalomban van, vagy egyenes vonalú egyenletes mozgást végez.![\[\Sigma \vec{F}=0\quad\Leftrightarrow\quad\vec{v}={\rm const.}\]](/images/math/2/f/9/2f9532c1b7495e753c298b57dc8e58a3.png)
![\[\Sigma\vec{F}=0\quad\Leftrightarrow\quad\vec{a}=\frac{\Sigma\vec{F}}{m}=0\quad\Leftrightarrow\quad\vec{v}={\rm const}\]](/images/math/4/2/6/426ee5c5a5c14d1268c0ce9b12b15309.png)
A törvény állításával („nyugalomban van”, „egyenes vonalú egyenletes mozgást végez”) kapcsolatban azonban fel kell tennünk egy kérdést: Mihez képest? Milyen koordinátarendszerhez képest van a test nyugalomban? Milyen koordinátarendszerhez képest végez egyenes vonalú egyenletes mozgást?
Hétköznapi tapasztalat, hogy egy hirtelen fékező járműben a járműhöz képest korábban nyugalomban lévő test látszólag minden ok nélkül gyorsulni kezd. A járműhöz rögzített koordinátarendszerben ez ellentmond Newton I. törvényének: a test ebből a koordinátarendszerből nézve annak ellenére gyorsul, hogy a rá ható erők eredője nulla. Ugyanakkor, ha a Földhöz rögzített koordinátarendszerben írjuk le a mozgást, akkor azt látjuk, hogy a jármű fékez (lassul, negatív gyorsulása van), a test viszont egyenes vonalú egyenletes mozgással halad tovább, összhangban Newton I. törvényével.
Hasonló a helyzet egy kanyarodó járműben. A járműhöz rögzített koordinátarendszerből vizsgálva a járműben lévő testek annak ellenére kifelé (a kanyarodással ellentétes irányban) gyorsulnak, hogy nem hat rájuk vízszintes erő – ismét ellentmondva Newton I. törvényének. A Földhöz rögzített koordinátarendszerből nézve viszont azt látjuk, hogy a járművön lévő testek – összhangban Newton I. törvényével – egyenes vonalú egyenletes mozgással haladnak tovább, miközben a jármű „elkanyarodik alóluk”. Eszerint vannak olyan koordinátarendszerek, amelyekből leírva a jelenségeket Newton I. törvénye teljesül, és vannak olyanok, amelyekben nem.
Azokat a koordinátarendszereket, melyekben teljesül Newton I. törvénye (azaz ha egy testre nem hat erő, vagy a rá ható erők eredője nulla, akkor a test ebben a koordinátarendszerben nyugalomban van, vagy egyenes vonalú egyenletes mozgást végez), inerciarendszernek nevezzük. Newton I. törvénye így nem más, mint az inerciarendszer definíciója. A Newton-törvények – eredeti formájukban – csak inerciarendszerekben igazak.
A definíció alapján látszólag könnyű eldönteni, hogy egy koordinátarendszer inerciarendszer-e. Azonban azt, hogy egy testre valóban semmilyen erő ne hasson, nehéz biztosítani. Sok feladat megoldásakor a Földhöz rögzített koordinátarendszer inerciarendszernek tekinthető. A Föld azonban forog, így a Földhöz képest nyugalomban lévő testek valójában körmozgást végeznek a Föld tengelye körül, és így gyorsulnak. Tehát a Földhöz rögzített koordinátarendszer nem inerciarendszer. (A forgás lassú, ezért lehet sok esetben mégis annak tekinteni.) Jobb közelítés a Föld középpontjához rögzített, de nem forgó rendszer. Ez azonban a Föld Nap körüli keringése miatt – sokkal kisebb mértékben – szintén gyorsul. A Nap középpontjához (pontosabban a Naprendszer tömegközéppontjához) rögzített koordinátarendszer már gyakorlatilag minden esetben inerciarendszerként használható.
A Galilei-féle relativitás elve alapján az egymáshoz képest nyugalomban lévő vagy egyenes vonalú egyenletes mozgást végző rendszereket mechanikai jelenségek alapján nem lehet megkülönböztetni. Így ha egy koordinátarendszer inerciarendszer, akkor a hozzá képest egyenes vonalú egyenletes mozgást végző test is inerciarendszer. Az inerciarendszerek közötti transzformáció a Galilei-transzformáció.
Gyorsuló és forgó koordinátarendszerek
Tehetetlenségi erő
A Newton-törvények eredeti formájukban csak inerciarendszerekben igazak. A korábban elemzett példákban a fékező vagy kanyarodó járművön lévő testek annak ellenére gyorsuló mozgást végeznek a járműhöz képest, hogy a rá ható erők eredője nulla. A járműhöz képest a fékező (menetiránnyal ellentétes irányban gyorsuló) járműben előrefelé, a kanyarodó (az ív középpontja felé gyorsuló) járműben pedig kifelé gyorsulnak. A járműhöz viszonyított, gyorsuló koordinátarendszerben vizsgálva a testek tehát úgy mozognak, mintha fékezéskor előrefelé, kanyarodáskor kifelé (általában pedig a jármű gyorsulásával ellentétes irányba) ható erők is hatnának rájuk.
Ezeket a fiktív (nem valóságos) erőket tehetetlenségi erőknek nevezzük. Bevezetésükkel a Newton-törvények gyorsuló koordinátarendszerekben is használhatóvá válnak:
Ha egy K inerciarendszerben egy pont helyét az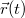 helyvektor adja meg, a hozzá képest egyenes vonalú gyorsuló mozgást végző K' rendszerben pedig az
helyvektor adja meg, a hozzá képest egyenes vonalú gyorsuló mozgást végző K' rendszerben pedig az 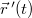 , akkor a két vektor között az
, akkor a két vektor között az ![\[\vec{r}(t)=\vec{r}\,'(t)+\vec{r}_{K'}(t)\]](/images/math/e/0/1/e013c57ef91a08b4ffa494bf56268d44.png)
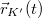 a K' rendszer origójának a helye a K rendszerhez viszonyítva. Ha a kifejezést kétszer deriváljuk idő szerint, akkor az
a K' rendszer origójának a helye a K rendszerhez viszonyítva. Ha a kifejezést kétszer deriváljuk idő szerint, akkor az ![\[\vec{a}(t)=\vec{a}\,'(t)+\vec{a}_0\]](/images/math/f/7/e/f7e16bc8a6e0579e15a353a7d2ba44f6.png)
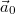 a K' rendszer gyorsulása a K rendszerhez képest. Az egyenlet mindkét oldalát megszorozva a tömegpont
a K' rendszer gyorsulása a K rendszerhez képest. Az egyenlet mindkét oldalát megszorozva a tömegpont  tömegével, és kihasználva, hogy a tömegpontra ható erők eredője a K inerciarendszerben
tömegével, és kihasználva, hogy a tömegpontra ható erők eredője a K inerciarendszerben 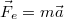 , az
, az ![\[\vec{F}_e=m\vec{a}\,'+m\vec{a}_0\]](/images/math/4/1/9/419fdee3b5b7386e0db9987608111e21.png)
egyenletet kapjuk. Ez azt mutatja, hogy a gyorsuló K' rendszerben nem teljesül Newton II. törvénye.
Ha azonban bevezetjük az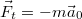 tehetetlenségi erőt, akkor
tehetetlenségi erőt, akkor ![\[\vec{F}_e=m\vec{a}\,'-\vec{F}_t\]](/images/math/b/1/0/b1001193c0ef19322eae2cb6f01bf520.png)
![\[\vec{F}_e'=\vec{F}_e +\vec{F}_t=m\vec{a}\,'\]](/images/math/6/8/0/6804850cc8206802a91a5c5fd374f761.png)
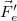 ), akkor a Newton II. törvény ebben a koordinátarendszerben is használhatóvá válik.
), akkor a Newton II. törvény ebben a koordinátarendszerben is használhatóvá válik.
Centrifugális erő és Coriolis-erő
Forgó koordinátarendszer esetében a gyorsuló koordinátarendszerhez hasonlóan fiktív tehetetlenségi erők bevezetésével érhetjük el, hogy a Newton-törvények használhatók legyenek.
Ha a K' rendszer 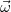 szögsebességgel forog a K inerciarendszerhez képest, akkor a K' rendszerben a valódi erőkön kívül általános esetben három fiktív erőt kell felvenni:
szögsebességgel forog a K inerciarendszerhez képest, akkor a K' rendszerben a valódi erőkön kívül általános esetben három fiktív erőt kell felvenni:
Az 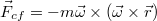 centrifugális erő minden testre „hat”, az
centrifugális erő minden testre „hat”, az 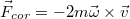 Coriolis-erő viszont csak a K' rendszerhez képest mozgó testekre. Az Euler-erő bevezetésére csak gyorsulva forgó koordinátarendszer esetén van szükség, ezzel nem foglalkozunk.
Coriolis-erő viszont csak a K' rendszerhez képest mozgó testekre. Az Euler-erő bevezetésére csak gyorsulva forgó koordinátarendszer esetén van szükség, ezzel nem foglalkozunk.
A kifejezésekben az 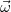 a szögsebesség-vektor (ennek nagysága a szögsebesség, iránya pedig a forgás tengelye), a
a szögsebesség-vektor (ennek nagysága a szögsebesség, iránya pedig a forgás tengelye), a  jel pedig a vektoriális szorzat jele. Ezeknek a tehetetlenségi erőknek a használatát a forgó Földhöz rögzített koordinátarendszer esetében mutatjuk meg.
jel pedig a vektoriális szorzat jele. Ezeknek a tehetetlenségi erőknek a használatát a forgó Földhöz rögzített koordinátarendszer esetében mutatjuk meg.
A Csodák palotájában a Coriolis-erő közvetlenül is megtapasztalható a Coriolis-szobában. A centrifugális erő élményéről pedig Truffaut Négyszáz csapás című filmjében van egy szép jelenet.
Valódi erők és tehetetlenségi erők
A valódi erők és a gyorsuló koordinátarendszereknél bevezetett fiktív tehetetlenségi erők között lényeges különbségek vannak.
A valódi erők mindig két test közötti kölcsönhatás kifejezői. Mindig megtalálható az a másik test, amivel a vizsgált test kölcsönhat, és mindig teljesül Newton III. törvénye (hatás-ellenhatás).
A tehetetlenségi erők fiktív, nem valóságos erők. Gyorsuló koordinátarendszerekben azért vezetjük be, hogy Newton II. törvénye használható legyen. Ezek nem kölcsönhatást fejeznek ki, nem lehet megtalálni a kölcsönható másik testet. Ugyanakkor a gyorsuló koordinátarendszerben leírva a mozgást ezek az erők ugyanúgy hatnak a testekre, mint a valóságos erők.
Tehetetlenségi erők a forgó Földön
Gravitációs erő és nehézségi erő
A forgó Föld nem inerciarendszer, azonban a földi jelenségeket mégis legtöbbször a Földhöz rögzített koordinátarendszerben érdemes leírni. Ahhoz, hogy a Newton-törvények használhatók legyenek, a testekre ható valódi erőkön kívül a forgás miatt fellépő fiktív, tehetetlenségi erőket: a centrifugális erőt és Coriolis-erőt is figyelembe kell venni. (A Föld forgása jó közelítéssel egyenletes, így Euler-erő nem lép fel. A Föld Nap körüli keringésének hatása pedig legtöbbször elhanyagolható.)
A két erő közül a centrifugális erő okoz kevesebb problémát: ennek az erőnek a nagysága nem függ a test mozgásállapotától. A centrifugális erő sok szempontból hasonlóan viselkedik, mint a gravitációs erő, hiszen arányos a test tömegével, és ezen kívül csak a test helyétől függ: 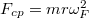 , ahol
, ahol 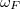 a Föld szögsebessége,
a Föld szögsebessége,  pedig a test távolsága a Föld forgástengelyétől.
pedig a test távolsága a Föld forgástengelyétől.
A forgó koordinátarendszerből megfigyelve nem lehet szétválasztani a két erőt, minden testre a két erő eredője hat. A gravitációs erő (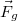 ) a Föld középpontja felé, a centrifugális erő (
) a Föld középpontja felé, a centrifugális erő (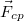 ) pedig a forgástengelyre merőleges irányban, kifelé mutat. A két erő eredője az
) pedig a forgástengelyre merőleges irányban, kifelé mutat. A két erő eredője az 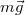 nehézségi erő (8. ábra). A nehézségi erő és a gravitációs erő tehát (a sarkokat kivéve) kis mértékben eltér egymástól, a legnagyobb (kb. 0,3 %) eltérés az egyenlítőnél van. A két erőnek általában az iránya is eltér egymástól: a nehézségi erő a sarkokat és az egyenlítőt kivéve nem a Föld középpontjába mutat. A nehézségi erő iránya definíció szerint az adott helyen a függőleges irány, az erre merőleges sík pedig a vízszintes. A tengerszint – amihez a földrajzi magasságokat mérik – emiatt nem gömbfelület, hanem egy lapult forgási ellipszoid.
nehézségi erő (8. ábra). A nehézségi erő és a gravitációs erő tehát (a sarkokat kivéve) kis mértékben eltér egymástól, a legnagyobb (kb. 0,3 %) eltérés az egyenlítőnél van. A két erőnek általában az iránya is eltér egymástól: a nehézségi erő a sarkokat és az egyenlítőt kivéve nem a Föld középpontjába mutat. A nehézségi erő iránya definíció szerint az adott helyen a függőleges irány, az erre merőleges sík pedig a vízszintes. A tengerszint – amihez a földrajzi magasságokat mérik – emiatt nem gömbfelület, hanem egy lapult forgási ellipszoid.
Súlyos és tehetetlen tömeg, az Eötvös-kísérlet
A tömeg két alapvető fizikai összefüggésben is szerepel: Newton II. törvényében és az általános tömegvonzás törvényében is.
A tömeg fogalmát Newton II. törvénye kapcsán vezettük be: az 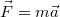 összefüggés megadja, hogy mekkora erő kell egy test gyorsításához. Az összefüggés alapján a tömeget definiálhatjuk a következőképpen: egységnyi tömeg az, amit egységnyi erő egységnyi gyorsulással gyorsít. Ebben a definícióban a tömeg a test „tehetetlenségét” fejezi ki, ezért szokás tehetetlen tömegnek nevezni.
összefüggés megadja, hogy mekkora erő kell egy test gyorsításához. Az összefüggés alapján a tömeget definiálhatjuk a következőképpen: egységnyi tömeg az, amit egységnyi erő egységnyi gyorsulással gyorsít. Ebben a definícióban a tömeg a test „tehetetlenségét” fejezi ki, ezért szokás tehetetlen tömegnek nevezni.
A Newton-féle gravitációs törvény két tetszőleges test közötti vonzóerőt adja meg. Ez az erő a tapasztalat szerint a testek távolságán kívül a testek tömegétől függ. A törvény alapján a tömeget definiálhatjuk a következőképpen is: egységnyi tömeg az, ami egy másik ugyanekkora tömeget egységnyi távolságból megadott erővel (az SI rendszerben 6,67∙10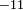 N) vonz. Ebben a definícióban a tömeg a test „gravitálóképességét” fejezi ki, ami a gyakorlatban a test súlyát okozza, ezért szokás súlyos tömegnek nevezni.
N) vonz. Ebben a definícióban a tömeg a test „gravitálóképességét” fejezi ki, ami a gyakorlatban a test súlyát okozza, ezért szokás súlyos tömegnek nevezni.
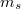 súlyos tömegével arányos, a Newton törvényben viszont a test
súlyos tömegével arányos, a Newton törvényben viszont a test 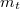 tehetetlen tömege szerepel. A szabadon eső test gyorsulása tehát
tehetetlen tömege szerepel. A szabadon eső test gyorsulása tehát ![\[a=\frac{m_s g}{m_t}=\frac{m_s}{m_t}g\]](/images/math/6/a/3/6a324dbb5fad41fbccf7e2b8054ebe6f.png)
A szabadon eső testek gyorsulása azonban nem mérhető kellő pontossággal. Eötvös Loránd a XX. század elején a róla elnevezett Eötvös-inga segítségével a kétféle tömeg ekvivalenciáját közel három nagyságrenddel pontosabban igazolta, mint a korábbi mérések. Az Eötvös-kísérlet alapja, hogy a forgó Földön a vékony torziós szálra erősített tömegekre a súlyos tömegekkel arányos gravitációs erő és a tehetetlen tömegekkel arányos centrifugális erő is hat. Eötvösnek sikerült kimutatnia, hogy a kétféle tömeg aránya különböző anyagok esetén legfeljebb 1:10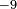 arányban tér el egymástól.
arányban tér el egymástól.
Az Eötvös-ingával mérni lehet a gravitációs erő nagyon kicsiny változásait is, amiből a földalatti tömegeloszlásra lehet következtetni, és így földgáz- és kőolajlelőhelyeket lehet megtalálni.
Coriolis-erő: szelek, tengeráramlatok, folyók
A Coriolis-erő csak a forgó koordinátarendszerhez képest mozgó testekre hat. Nagysága és iránya függ a test sebességétől, így nem lehet a centrifugális erőhöz hasonlóan kezelni.
A Coriolis-erő vektoriális kifejezéséből (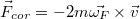 ) látszik, hogy az erő merőleges a Föld forgástengelyére és a test Földhöz viszonyított sebességére is, és minden olyan testnél fellép, amely nem a forgástengellyel párhuzamosan mozog. A Coriolis-erőnek számtalan hétköznapi életben megfigyelhető hatására van: a gyorsan mozgó lövedékek a kilövés irányától függően vízszintes és függőleges irányban is eltérülhetnek, a keleti és nyugati irányban mozgó testek súlya kis mértékben eltér egymástól, a szabadon eső testek pedig nem pontosan függőlegesen esnek.
) látszik, hogy az erő merőleges a Föld forgástengelyére és a test Földhöz viszonyított sebességére is, és minden olyan testnél fellép, amely nem a forgástengellyel párhuzamosan mozog. A Coriolis-erőnek számtalan hétköznapi életben megfigyelhető hatására van: a gyorsan mozgó lövedékek a kilövés irányától függően vízszintes és függőleges irányban is eltérülhetnek, a keleti és nyugati irányban mozgó testek súlya kis mértékben eltér egymástól, a szabadon eső testek pedig nem pontosan függőlegesen esnek.
A gyakorlati szempontból legfontosabb jelenség azonban a mozgó levegő- és víztömegekre ható Coriolis-erő. A nyomáskülönbségek miatt mozgó légtömegek a Coriolis-erő hatására eltérülnek, és hatalmas forgó rendszerek, úgynevezett ciklonok alakulnak ki. Az északi féltekén a forgás mindig óramutató járásával ellentétes, a délin pedig megegyező irányú. A Coriolis-erőnek fontos szerepe van a trópusokon a felszín közelében kelet felől fújó passzát szelek és a nagy magasságban a Földet körülérő nyugati irányú futóáramlások (jetek) kialakulásában is.
A Coriolis-erő a légtömegekhez hasonlóan a hőmérséklet- és a sókoncentráció-különbségek, a szél és az árapály hatására létrejövő tengeráramlatok mozgását is befolyásolja. A tengeráramlásokhoz hasonlóan a folyókra is hat a Coriolis-erő: az északi féltekén a folyók erősebben alámossák a jobb partjukat. A Visegrádnál a hegyeket áttörő Duna például folyamatosan vándorol nyugatra: ezt mutatják a folyó vándorlása után visszamaradt kiskunsági homokdombok és a jobb parton végig megtalálható leszakadó löszfalak (pl. Dunaújváros, Dunaföldvár).
Foucault-inga
A Föld forgását sok kísérleti tapasztalat mutatja. A csillagászati megfigyelések mellett éppen a forgás miatt fellépő tehetetlenségi erők adják a legközvetlenebb bizonyítékokat. Történetileg leghíresebb kísérlet az 1851-ben a párizsi Panthéonban bemutatott Foucault-inga. A mozgó ingára a Földhöz rögzített koordinátarendszerben hat a Coriolis-erő, és emiatt az inga lengési síkja lassan elfordul. Inerciarendszerből nézve az inga lengési síkja változatlan marad, és a Föld fordul el alatta. Az elfordulás sebessége függ a földrajzi helytől: a sarkokon egy csillag-nap alatt teljesen körbefordul, más helyeken viszont lassabban (az egyenlítőn pedig egyáltalán nem) fordul el.
Vissza a Fizika 1i nyitóoldalára
1. Tér és idő
2. Mozgás és megjelenítése
3. Megmaradási törvények a mechanikában
4. Rezgések
6. Hideg-meleg