„2. Mérés: Nemlineáris eszköz vizsgálata, oszcilloszkóp használata” változatai közötti eltérés
a |
a |
||
| 58. sor: | 58. sor: | ||
Próbáljuk ki a háromszög és négyszög jeleket is, különböző frekvenciákon! | Próbáljuk ki a háromszög és négyszög jeleket is, különböző frekvenciákon! | ||
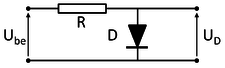
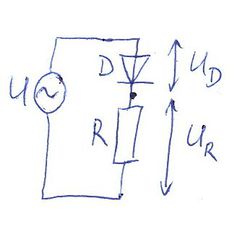
| − | '''2. Feladat''' A próbapanelen állítsuk össze az alábbi kapcsolást! Az R ellenállás legyen 1 k$\Omega$, a D pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U$_{be}$ bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre f=200 Hz frekvenciájú, | + | '''2. Feladat''' A próbapanelen állítsuk össze az alábbi kapcsolást! Az R ellenállás legyen 1 k$\Omega$, a D pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U$_{be}$ bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre f=200 Hz frekvenciájú, U$_{pp}$=1.6 V-os háromszög jelet. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást, valamint a triggert a felfutó élre. Honnan látható a dióda egyenirányító hatása? |
[[File:RD.png|225px|thumb|right|2. feladat kapcsolási rajz]] | [[File:RD.png|225px|thumb|right|2. feladat kapcsolási rajz]] | ||
A lap jelenlegi, 2023. november 15., 14:55-kori változata
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Áram-feszültség karakterisztika
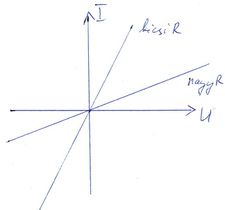
Ohmikus ellenállások áram-feszültség összefüggését Ohm törvénye adja meg:
![\[ I=\frac{1}{R}U, \]](/images/math/9/2/1/9211784a68cb1d6b23c5005cdbe41776.png) ahol |
Egyenirányító dióda
| Az egyenirányító dióda idealizált áram-feszültség összefüggése pozitív feszültségekre egy végtelen nagy, míg negatív feszültségekre egy nulla vezetőképességű ellenállással közelíthető. Pozitív feszültségek esetén nyitó- míg negatív feszültségek esetén záróirányról szokás beszélni. |
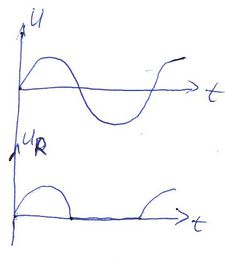
Ha megvizsgálunk egy szinuszos váltófeszültséggel táplált áramkört, melyben egy ilyen diódát egy  fogyasztóval sorba kapcsolunk, az fogyasztóval sorba kapcsolunk, az  ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget. A pozitív félperiodusban a dióda ellenállása elhanyagolható, így a teljes feszültség az ellenálláson esik. A negatív félperiodusban a dióda ellenállása dominálja az eredő ellenállást, hozzá képest az ellenálláson csak az egyik félperiodusban mérhetünk véges feszültséget. A pozitív félperiodusban a dióda ellenállása elhanyagolható, így a teljes feszültség az ellenálláson esik. A negatív félperiodusban a dióda ellenállása dominálja az eredő ellenállást, hozzá képest az  ellenállás elhanyagolható. ellenállás elhanyagolható.
|
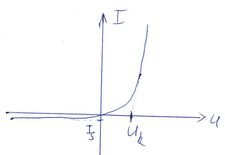
Valódi egyenirányító dióda áram görbéje összefüggése erősen aszimetrikus függvénye a feszültségnek. Pozitív feszültségek esetén egy kritikus érték, a nyitófeszültség felett az áram gyorsan növekszik. Félvezető Ge és Si dióda esetén 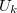 = 0,3..0,4 V illetve 0,6..0,7 V. Valós diódára kapcsolt negatív feszültség estén véges, ún. záróirányú áram folyik, mely tipikusan = 0,3..0,4 V illetve 0,6..0,7 V. Valós diódára kapcsolt negatív feszültség estén véges, ún. záróirányú áram folyik, mely tipikusan  A nagyságú. Egy általános A nagyságú. Egy általános 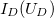 áram-feszültség karakterisztikával rendelkező diódával sorba kapcsolt áram-feszültség karakterisztikával rendelkező diódával sorba kapcsolt  ellenállás esetén a körben folyó áramot illetve a diódán és az ellenálláson eső feszültségeket grafikusan tudjuk meghatározni. A körben azonos ellenállás esetén a körben folyó áramot illetve a diódán és az ellenálláson eső feszültségeket grafikusan tudjuk meghatározni. A körben azonos 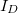 áram halad át a diódán és az ellenálláson is, a körben eső feszültségekre pedig teljesül: áram halad át a diódán és az ellenálláson is, a körben eső feszültségekre pedig teljesül:
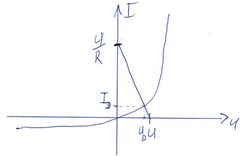
![\[U=U_D+RI_D\]](/images/math/7/c/5/7c509f3a40fdd4eb0c5a06be2270f866.png) összefüggés, melyet átrendezve kapjuk a grafikus megoldáshoz szükséges alakot: ![\[\frac{U-U_D}{R}=I_D(U_D).\]](/images/math/3/8/5/3850a7c2a1377ccc88737e83970d9a6d.png) Az egyenlet bal oldala egy egyenest ír le, míg a jobboldalon a dióda áram-feszültség karakterisztikája látható. |
Mérésben használt műszerek
A mérésben a National Instruments myDAQ digitalizálókártya által szintetizált váltakozó feszültség jelet illetve a mérőkártya által megvalósított oszcilloszkópot fogjuk használni. Egy analóg oszcilloszkóp működését az alábbi leírás taglalja: [[1]]. A mérőkártya hasonló oszcilloszkópot valósít meg digitálisan.
Mérési feladatok
1. Feladat A függvénygenerátor jelét vizsgáljuk oszcilloszkóp segítségével! A függvénygenerátor jele a myDAQ mérőkártya AO 0 illetve AGND (referencia) pontja között jelenik meg. A váltóáramú jelet csatlakoztassuk a kártya AI 0+, AI 0- bemenetére. Az ELVIS program FGEN nevű függvénygenerátorával hozzunk létre f=275 Hz frekvenciájú és V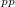 =1 V (peak-to-peak) amplitúdójú szinusz jelet. A \emph{Scope} programon állítsuk be a triggert a felfutó élre, majd a feszültségerősítést és az időosztást a megfelelő értékre. Rögzítsük a feszültség időfüggését! Az oszcilloszkóp program STOP gombjának megnyomása után, a LOG gombbal mentsük el a mért jelalakokat.
=1 V (peak-to-peak) amplitúdójú szinusz jelet. A \emph{Scope} programon állítsuk be a triggert a felfutó élre, majd a feszültségerősítést és az időosztást a megfelelő értékre. Rögzítsük a feszültség időfüggését! Az oszcilloszkóp program STOP gombjának megnyomása után, a LOG gombbal mentsük el a mért jelalakokat.
A kiértékeléshez a MATLAB segítségével olvassuk be a jeleket. A fejléc (header) kezeléséhez használjuk a textscan parancsot vagy a MATLAB grafikus file import funkcióját. (Figyelem, az oszcilloszkóp időalapjának változtatásával változik a mintavételezés is!) Illesszünk szinusz görbét, és az illesztésből határozzuk meg a jel frekvenciáját és amplitúdóját, majd vessük össze a beállított értékekkel.
Próbáljuk ki a háromszög és négyszög jeleket is, különböző frekvenciákon!
2. Feladat A próbapanelen állítsuk össze az alábbi kapcsolást! Az R ellenállás legyen 1 k , a D pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U
, a D pedig egy (Schottky) dióda. Az ellenálláson és a diódán eső feszültségeket kapcsoljuk a mérőkártya AI 0+, AI 0- illetve AI 1+, AI 1- csatlakozói közé. U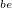 bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre f=200 Hz frekvenciájú, U
bemenetre csatlakoztassuk a myDAQ mérőkártya AO 0 illetve AGND (referencia pont) kimenetét, és a függvénygenerátor segítségével kapcsoljunk a bemenetre f=200 Hz frekvenciájú, U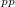 =1.6 V-os háromszög jelet. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást, valamint a triggert a felfutó élre. Honnan látható a dióda egyenirányító hatása?
=1.6 V-os háromszög jelet. Az oszcilloszkóp mindkét csatornáját kapcsoljuk be, majd állítsuk be a feszültségerősítést, időosztást, valamint a triggert a felfutó élre. Honnan látható a dióda egyenirányító hatása?
Rögzítsük mindkét csatornán a feszültség időfüggését, majd a MATLAB segítségével dolgozzuk fel a jeleket. Az ellenálláson eső feszültségből számítsuk ki a körben folyó áramot és ábrázoljuk a dióda áram-feszültség karakterisztikáját. Adjunk becslést a nyitófeszültségre! Ehhez érdemes ábrázolni a áram logaritmusát a feszültség függvényében. Az ideális dióda I-V görbéjét az alábbi formula adja meg:
![\[ I=I_0(exp^\frac{eU}{kT}-1) \]](/images/math/2/e/d/2ed147c1dbc8c8a8b6c7f25873c79f84.png)
ahol 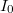 a szaturációs áram,
a szaturációs áram,  az elektron töltése,
az elektron töltése,  a Boltzmann állandó és
a Boltzmann állandó és  az abszolút hőmérséklet. A mért görbére illesszük a fenti formulát, majd a terem hőmérsékletének ismeretében határozzuk meg az elemi töltés és a Boltzmann állandó hányadosát, és hasonlítsuk össze azt az irodalomból ismert adattal!
az abszolút hőmérséklet. A mért görbére illesszük a fenti formulát, majd a terem hőmérsékletének ismeretében határozzuk meg az elemi töltés és a Boltzmann állandó hányadosát, és hasonlítsuk össze azt az irodalomból ismert adattal!
 az
az  pedig a rajta eső feszültség. A vezetőképességet -
pedig a rajta eső feszültség. A vezetőképességet - 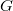 - az ellenállás inverzeként szokás definiálni, mértékegysége Siemens (1
- az ellenállás inverzeként szokás definiálni, mértékegysége Siemens (1  = 1
= 1 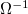 ). Általános esetben azonban az
). Általános esetben azonban az 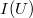 görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete.
görbe nemlineáris, melyre példa az egyenirányító dióda alább tárgyalt esete.
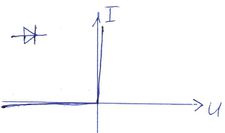
 ideális diódából és
ideális diódából és