„Szilárdtestfelületek analízise Auger elektron spektroszkópiával” változatai közötti eltérés
Lenk (vitalap | szerkesztései) |
Lenk (vitalap | szerkesztései) |
||
| 120. sor: | 120. sor: | ||
Ezután a vizsgált minta x. komponensének koncentrációját a következő összefüggéssel számolhatjuk atomszázalékban: | Ezután a vizsgált minta x. komponensének koncentrációját a következő összefüggéssel számolhatjuk atomszázalékban: | ||
<!--{{eq|{{C_x {{=}} \frac{ \frac{I_x}{1}}{2}}}|eq:4|(4)}}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}}}{x}{\frac {I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}}} \cdot 100%|eq:4|(4)}}--> | <!--{{eq|{{C_x {{=}} \frac{ \frac{I_x}{1}}{2}}}|eq:4|(4)}}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}}}{x}{\frac {I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}}} \cdot 100%|eq:4|(4)}}--> | ||
| − | {{eq|C_x {{=}} \frac{I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}} / {I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}} \cdot 100|eq:4|(4)}} | + | {{eq|C_x {{=}} \frac{I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}} |eq:4|(4)}}/ {I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px}} \cdot 100|eq:4|(4)}} |
A lap 2012. november 13., 06:28-kori változata
Tartalomjegyzék |
Szerkesztés alatt!
Elméleti összefoglaló
Az AES módszer fizikai alapjai
Pierre Auger francia fizikus röntgensugárzással gerjesztett argon atomok gerjesztési folyamatainak Wilson-féle ködkamrában történő tanulmányozása folyamán fedezte fel a róla elnevezett effektust 1925-ben. Ezt követően csak kb. 40 év után kezdődött el az AES módszer széleskörű gyakorlati felhasználása.
Napjainkban az AES módszert elsősorban szilárdtest felületek vizsgálatára alkalmazzák. Ennek folyamán a vizsgálandó felületet valamilyen primer gerjesztés hatásának tesszük ki, ami elsősorban 1-10 keV-os elektronnyalábbal való bombázást jelent, de elektromágneses sugárzás vagy ionnyaláb is lehet a gerjesztő hatás. Az ekkor végbemenő Auger-folyamatot az 1. ábrán szemléltetjük, és az alábbiak szerint értelmezzük.
Egy belső, például a K-héjon lévő elektront a primer részecske eltávolít az atomi kötelékből. Az így szabaddá váló energianívóra egy magasabb, például az L1 nívóról lép be egy elektron. A felszabaduló energiát például az L2 nívón lévő elektron veszi át, ami egy jól meghatározott, karakterisztikus energiával kilép a felületből. Ezt az elektront nevezzük KL1L2, vagy általánosabban KLL Auger-elektronnak. Itt jegyezzük meg, hogy a gyakorlat számára legfontosabb, nagy elektronhozammal rendelkező Auger-elektronok esetén az Auger-folyamatban résztvevő második, és harmadik elektronhéj egybeesik, így az anyagok zöménél a KLL, LMM Vagy MNN Auger-elektronok a (leggyakoribbak. (Az Auger-spektroszkópia fizikai alapjairól és alkalmazási területeiről ad áttekintést az /1/, /2/, /3/ szakirodalom.)
A K-héjon lévő megüresedett hely jelenléte esetén az L-héjon tartózkodó elektron energiaviszonyai hasonlóak azokhoz, melyekkel a hidrogénszerű ionokban lévő L-elektronok rendelkeznek. A finomstruktúrát most nem számítva, a küIönbség annyi, hogy a +Ze töltés (Z a rendszám, "e" az elemi töltés), amely meghatározza azt az elektromos teret, melyben az L-héjból a K-héjba átmenő elektron van, a mag +Ze valódi töltésénél a mag töltését leárnyékoló elektron töltésével kisebb. Természetesen a pontosabb leírásnál figyelembe kell azt is venni, hogy energetikailag három különböző L-állapot lehetséges. A továbbiakban tekintsük át röviden egy, az atomból emittálódó Auger-elektron energiáját meghatározó tényezőket. Egy tetszőleges, W X, és Y elektronhéjak által megvalósított Auger folyamatban keletkező Auger-elektron EW,X,Y(Z) energiája nemcsak az elektronhéjak EW, Ex és EY ionizációs energiáitól, illetve az illető elem Z rendszámától függ. Ezt az energiaértéket több tényező is befolyásolja, melyek közül a három legfontosabb a következő:
- Az EW, Ex és EY értékek általában az egyszeresen ionizált állapothoz tartozó ionizációs energiák, míg az Auger-folyamatnál a végső állapot hétszeresen ionizált.
- A szilárdtesteknél az elektronnak a vákuumba való vitelekor az energiamérlegnél figyelembe kell venni az elektron kilépési munkáját (Eki) is.
- Az Auger-elektronok energiáját a mátrix-környezet is befolyásolja, vagyis az, hogy milyen elemekkel, vegyületekkel és milyen módon kötött az elektront emittáló atom.
Az első két szempontot is figyelembe véve, az Auger-elektron energiája az alábbi félempirikus összefüggéssel adható meg:
![\[E_{WXY}(Z) =E_W(Z) - E_X(Z) - E_Y(Z + d) - E_{ki}\]](/images/math/6/a/d/6adccb3c004b144b53911fc4c4400502.png)
ahol a d korrekciós tag értéke az anyagi minőségtől függően 1/2 és 3/4 közé esik. Az Auger-energiák értekei a 2. ábrán tálhatók.
A harmadik perturbáló hatást, az un. kémiai eltolódást (chemical shift) nehéz mennyiségileg pontosan meghatározni, mivel nagyságát 3 energiaszint változása is befolyásolja. Általában azt mondhatjuk, hogy egy WXY Auger-átmenetnél a kémiai eltolódás nagysága:
![\[\Delta E = E_W - E_X - E_Y - \left (E_W + \Delta W - E_X - \Delta X - E_Y - \Delta Y \right )= \Delta W + \Delta X + \Delta Y\]](/images/math/8/e/1/8e1831896425deccb9f69c0c6672b3a7.png)
ahol a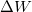 
, 
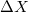és 
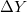a megfelelő W, X és Y elektronhéjak energiaeltolódósai, amelyeknek a mátrix- környezettől függő nagyságai nem egyenlőek. A helyzetet tovább komplikálja, ha az Auger-átmenetben a valencia-sáv is részt vesz.
A tanszéki Iaboratóriumban az AES méréseket egy un. SAM (Scanning Auger Microprobe) berendezésen végezzük. A SAM módszer az eddig tárgyalt AES módszertől elviekben nem különbözik, amennyiben a módszer alapja a SAM-nál is az emittált Auger-elektronok energiaanalízise, majd ez alapján a minta összetevőinek megállapítása. A különbség a két módszer között az, hagy a SAM-nál lehetőség van a primer elektronnyaláb pásztázására, és ezáltal egyrészt a vizsgálandó mintafelület topográfiai kepét lehet megjeleníteni, másrészt -és ez a fő előnye- a pásztázás révén mód van arra, hogy egyes kiválasztott elemeknek felvegyük és szükség esetén lefényképezzük a felületi eloszlás képét.
Az emittált Auger elektron-áramot meghatározó tényezők
Az előzőekben már láttuk, hogy a vizsgálandó mintafelületből a becsapódó primer elektronok karakterisztikus energiája Auger-elektronokat váltanak ki. Az alábbiakban ismertetjük az elektron hozamot meghatározó tényezőket. Legyen az i. elemben a WXY Auger-átmenetnél keletkező, és a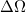 
térszögú akceptancia (fogadó) nyílással rendelkező AES berendezés által detektált Auger elektronáram 
.
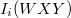Ekkor első közelítésben:
![\[I_i(WXY) = \frac{\Delta \Omega}{4\pi} \int\limits_0^{\infty} I_p(z) \cdot P_i(WXY) \cdot \sigma_i(E_W) \cdot N(z) \cdot X_i(z) \cdot F \left ( \alpha \right ) \cdot T(E_{WXY}) \cdot D(E_{WXY}) \cdot \exp \left [\frac{-z}{\lambda_i \cos \alpha}\right] dz\]](/images/math/3/9/b/39b955c8a0f1d97358e0350d6ec5437f.png)
ahol
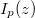a gerjesztő áramerőssége mélységben,
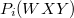annak a valószínűsége, hogy a gerjesztett atomnak a W-héj ionizációja után Auger-folyamat következik be,
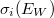a W-héj ionizációs hatáskeresztmetszete,
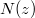a z mélységben lévő atomsűrűség,
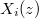az i. elem z mélységben lévő koncentrációja (atomtörtben),
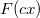az 
emissziós szögtől függő felületi érdességi faktor,
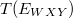az elektron energia spektrométer válaszfüggvénye,
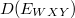az elektron detektor transzmissziója,
az i. elemből kilépő elektron közepes szabad úthossza.
Megjegyezzük, hogy a kémiai környezet hatását beleértettük az egyes paraméterek értékeibe, tehát például a 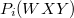vagy értéke ugyanarra az i. elemre is más érték, attól függően, hogy tiszta anyagból, vagy kémiailag kötött állapotban lévő anyagból származnak az Auger-elektronok. Ha figyelembe vesszük a szögeloszlást is, azaz széles szögtartományban vizsgáljuk az Auger elektronhozamot, továbbá figyelembe vesszük azt, hogy a paraméterek egy része a gerjesztő primer energiától is függ, akkor a következő alakot nyerjük:
![\[I_i(WXY) = \frac{1}{4\pi} \int\limits_{\Omega} \int\limits_0^{\infty} \int\limits_0^{(E_p)}I_p(E,z)\left [ I\neq r_b(E)\right] P_i(WXY) \cdot \sigma_i(E_pE_W) \cdot N(z) \cdot X_i(z) \cdot F(\alpha) \cdot T(E_{WXY}) \cdot D(E_{WXY}) \cdot \exp \left[ \frac{-z}{\lambda_i(E_p) \cdot \cos \alpha}\right] \cdot dE \cdot dz \cdot d\Omega\]](/images/math/3/e/5/3e5f449d58f1adce5f9c8c5662123618.png)
ahol rb a visszaszórási tényező. (A szakirodalomban szokásos az 1+rb értéket visszaszórási tényezőnek nevezni)
Általában elmondható, hogy a (4)-ben szereplő tényezők a kísérleti körülményeknek és a mátrix-környezetnek bonyolult függvényei. Az Ip-t alkotó primer elektronok energiájáról elmondható, hogy az Auger-elektronok szökési mélységén belül a primer energia csökkenése elhanyagolható.
A SAM berendezés ismertetése
A vizsgálandó minta felületének gerjesztését fókuszált, mozgatható elektron nyalábbal végezzük, míg mintatisztítás, illetve mélységi elemeloszlás felvétel céljára ionnyalábbal való bombázásra is lehetőség van, amint ez a SAM berendezés elvi felépítését bemutató 3. ábrán látható. A készülék konkrét kezelésének bemutatatására a mérési feladatokat ismertető részben, a 7. ábra alapján kerül sor.
Az elektronágyú tartalmazza a volfrámszálas elektronforrást, a gyorsító, a fókuszáló és az eltérítő elektródákat. Az elektronágyú-szabályozó egység gondoskodik a fókuszáláshoz és gyorsításhoz szükséges feszültségekről és a katód fűtéséről. A pásztázást-szabályozó egység biztosítja a fókuszált elektron-nyaláb eltérítését, valamint a TV, illetve display egységnek az eltérítéssel szinkronizált- feszültséggel való ellátását.
A mintából emittált Auger-elektronok energia szerinti szétválasztását az elektronágyú köré elhelyezett CMA (hengeres tükör analizátor) típusú energiaanalizátor végzi. Az ilyen fajta energiaanalizátor a vizsgálni kívánt E energia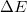 
környezetébe eső energiájú elektronokat engedi át. A 
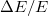mennyiség az analizátor energia-felbontása, ami az alkalmazott konkrét berendezésnél állítható, és 0,3%, 0,6% valamint 1,2% lehet. Az energiaanalizátor-szabályozó egység által szolgáltatott feszültség egy konkrét értékénél csak adott energiájú elektronok képesek a hengeres analizátor terét a szaggatott vonallal jelöIt pályán befutni.
A feszültség változtatásával tehát az elektronok energia spektruma vehető fel. Az energiájuk szerint megszűrt elektronok az elektronsokszorozóba kerülnek, majd jelerősítés után az Auger-spektroszkóp elektronikája dolgozza fel a továbbított elektromos jeleket differenciális üzemmódban. Az így előállított differenciális energiaspektrum írószerkezettel, vagy egyéb display egységgel jeleníthető meg.
A SAM berendezés a vizsgált minta felületének alapvetően kétfajta képét tudja előállítani. Az első fajta képpé a vizsgálatok elején a felületnek a vizsgálatok szempontjából érdekesebb részeiről való előzetes tájékozódás céljából felvehető az un. mikrográf vagy mikrodiagram, amely egy elektronmikroszkópos képre hasonlít, és a felület optikai képét adja. Ezt a képet vagy a szekunder elektronáramnak, vagy az elnyelt target-áramnak pontról-pontra történő regisztrálásával és megjelenítésével kaphatjuk meg. Az első esetben a képet röviden szekunder elektron-képnek, a második esetben abszorbeált áram-képnek nevezzük.
A másik fajta képet, amely egy adott elem felületi eloszlását mutatja, Auger eloszlás-képnek nevezik. Ez úgy készül, hogy a kérdéses elem adott energiájú elektronjaitól származó "Auger"-jeleket folyamatosan regisztráljuk, miközben a minta felületét folyamatosan pásztázzuk a primer elektronnyalábbal.
Lehetőség van az elemek mélység szerinti eloszlásának nyomon követésére is, mégpedig oly módon, hogy a primer ionágyúval előállított ionokkal bombázzuk a minta (target) felületét, amelyről folyamatosan porlódnak le az atomrétegek. Eközben a kiválasztott elemek Auger elektron intenzitásának folyamatos kijelzésével felvehető ezen elemek mélységi eloszlásgörbéje.
A SAM berendezés néhány fontosabb mérési paramétere a következő:
- primer elektron energia:5 keV, de egyébként 0,5-10 keV között változtatható,
- primer elektron áramerősség: általában néhány tized
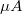, de egyébként 2 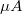-ig változtatható,
- primer elektron nyaláb átmérő: kb.
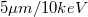és 10-7A értéknél), és kb. 
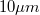15 keV és 10-6 A értéknél),
- laterális felbontóképesség: kb. 5
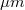, közel azonos a primer elektron nyaláb legkisebb átmérőjével,
- energiafelbontóképesség: 0,3%, 0,6%, 1,2% /állítható/,
- porlasztó ionenergia: 5 keV-ig változtatható,
- porlasztó ionáram: 10-9 -10-6 A között állítható,
- egyszerre behelyezhető minták száma: max.12 db,
- kifűthetőség: 250 °C-ig,
- sztatikus végvákuum: kb.
.
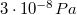Mérési feladatok
Ötvözet-minta összetételének meghatárzása
A méréshez szükséges eszközök:
- acél-etalon minta (a mérés kezdetén már a vákuumkamra mintatartójára helyezve),
- SAM berendezés,
- Vákuummérő,
- Dewar-palack cseppfolyós nitrogénnel töltve.
Az előzőekben már láttuk, hogy az Auger-elektronok intenzitását számos mátrixfüggő és berendezésfüggő paraméter befolyásolhatja. Ezek közül sok paraméternek a hatásától eltekinthetünk, ha néhány egyszerűsítő körülménnyel és feltételezéssel élünk. Az első az, hogy az információs mélységen belül eltekintünk ugyanazon elem koncentrációbeli inhomogenitásaitól, tehát megelégszünk azzal, hogy a legfelső atomrétegek átlagos összetételét határozzuk meg. Ugyanakkor laterális vonatkozásban, a primer gerjesztő nyaláb keresztmetszetének megfelelő területen belül szintén eltekintünk a minta alkotóinak koncentrációbeli inhomogenitásaitól, tehát e tekintetben is csak átlagértéket határozunk meg. A következő egyszerűsítés az, hogy eltekintünk a felületi érdességi faktor szerepétől. Ezt azért vagyunk kénytelenek megtenni, mert a mérés (és a porlasztás) alatt egyszerűen nincs idő a minta egyedi felületi geometriai sajátságainak pontos feltérképezésére. Az ebből származó hibát úgy csökkentjük, hogy simára polírozott felületeket, vagy a gerjesztő elektronnyaláb alatt síknak tekinthető szemcsehatárokat vizsgálunk.
További egyszerűsítésre nyílik lehetőség, ha meggondoljuk, hogy a mátrixkörnyezet elsősorban az elemek legkülső elektronhéjainak energiaviszonyait befolyásolja, és a mélynívókra gyakorolt hatása sokkal kisebb jelentőségű, esetenként elhanyagolható. Így, ha a mennyiségi kiértékelésnél azokat az Auger elektronenergia csúcsokat használjuk fel, amelyeknek a kialakításában a mélynívók vesznek részi, akkor (hacsak nem kémiai vegyületet vizsgálunk) egy hasonló összetételű etalonmintával, vagy csak a vizsgált elemeket tartalmazó tiszta anyaggal történő összehasonlításnál az Auger-folyamat-keltés valószínűségében és az ionizációs hatáskeresztmetszetben fellépő változások elhanyagolhatóak. Továbbá, ha a vizsgált minta-ötvözet a periódusos rendszerben közeli rendszámú fémes elemekből áll, amelyeknél az elektron közepes szabad úthossz és a visszaszórási tényező értékek közel azonosak, akkor a mennyiségi kiértékelésre néhány százalékos relatív hibával alkalmas az un. relatív érzékenységi tényezők módszere. Ennél a módszernél a minták összetételének meghatározására felhasználjuk az ugyanazon típusú berendezésen egy ezüst-etalon mintára normált érzékenységi faktorokat a különböző elemek esetén (SX). Ezek az értékek : 3 keV, 5 keV és 10 keV primer elektronenergiákra a 4., 5. és 6, ábrákról olvashatók le.
Ezután a vizsgált minta x. komponensének koncentrációját a következő összefüggéssel számolhatjuk atomszázalékban:
\[C_x = \frac{I_x}{S_x \cdot L_x \cdot E_{mx} \cdot I_{px\]
