„Optikai heterodin detektálás” változatai közötti eltérés
Lenk (vitalap | szerkesztései) a |
Lenk (vitalap | szerkesztései) a |
||
| 161. sor: | 161. sor: | ||
A mérést az [[#fig:1|1. ábra]] szerinti interferométerrel végezzük el, amelyben természetesen csak akkor kapunk eredményt, ha x<sub>0</sub> elég nagy. Amennyiben $x_0 < \lambda/8$, akkor nullahelyek nem lépnek fel, így ez az eljárás nem alkalmazható. (Ekkor csak a heterodin jel spektrális vizsgálata adhat információt az amplitudóról.) Ezért a heterodin jel nullátmeneteinek számlálásával az alkalmazott lézerfény hullámhosszánál ($\lambda_{He-Ne} {{=}} 633 nm$) nagyobb amplitúdójú rezgéseket lehet csupán vizsgálni. Ha a nullátmenetek között eltelt idők reciprokát képezzük, akkor ezek úgy tekinthetők, mint a t<sub>i</sub> és t<sub>i+1</sub> időpontok közötti pillanatnyi frekvencia, így ezen időközök $\Delta \tau_{i} {{=}} t_{i+1}-t_i$ | A mérést az [[#fig:1|1. ábra]] szerinti interferométerrel végezzük el, amelyben természetesen csak akkor kapunk eredményt, ha x<sub>0</sub> elég nagy. Amennyiben $x_0 < \lambda/8$, akkor nullahelyek nem lépnek fel, így ez az eljárás nem alkalmazható. (Ekkor csak a heterodin jel spektrális vizsgálata adhat információt az amplitudóról.) Ezért a heterodin jel nullátmeneteinek számlálásával az alkalmazott lézerfény hullámhosszánál ($\lambda_{He-Ne} {{=}} 633 nm$) nagyobb amplitúdójú rezgéseket lehet csupán vizsgálni. Ha a nullátmenetek között eltelt idők reciprokát képezzük, akkor ezek úgy tekinthetők, mint a t<sub>i</sub> és t<sub>i+1</sub> időpontok közötti pillanatnyi frekvencia, így ezen időközök $\Delta \tau_{i} {{=}} t_{i+1}-t_i$ | ||
mérésével a pillanatnyi sebesség abszolút értéke is meghatározható az alábbi összefüggés alapján (de az előjele nem): | mérésével a pillanatnyi sebesség abszolút értéke is meghatározható az alábbi összefüggés alapján (de az előjele nem): | ||
| − | {{eq|\frac{1}{2\Delta \tau_i} {{=}} | + | {{eq|\frac{1}{2\Delta \tau_i} {{=}} (f_i) \sim \frac{2|v|}{\lambda }|eq:40|(40)}}--> |
==Mérési feladatok== | ==Mérési feladatok== | ||
A lap 2012. november 24., 10:08-kori változata
Tartalomjegyzék[elrejtés] |
Szerkesztés alatt!
Elméleti összefoglaló
A hullám fogalma – a fény mint hullám
A fény, mint ismeretes, az elektromágneses tér hullámjelensége. Jellemző rezgési frekvenciája a 1014 Hz körüli tartományba esik. Az a fizikai mennyiség, amelynek terjedését egyszerűen fénynek nevezzük, az elektromos és mágneses térerősség. Tehát a fényben az elektromos és a mágneses tér változásai terjednek. Tekintsünk egy, a tárgyalás szempontjából egyszerű, lineárisan polarizált harmonikus síkhullámot. A síkhullám elnevezés onnan ered, hogy az azonos térerősségű pontok egy adott pillanatban egy síkon helyezkednek el. A síkhullám kifejezése:
![\[{{E\left( \mathbf{r},t \right) = {E_0}\cos \left( \omega t - \mathbf{kr} \right)}}\]](/images/math/f/6/d/f6dbdb46476464b9d6662507a6419707.png)
ahol E0 az elektromos hullám amplitúdója, k a hullámszám vektor, 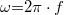 az elektro-mágneses hullám körfrekvenciája, „f” pedig a frekvenciája. Egyszerű megfontolásokból a hullám terjedési sebessége k-val és
az elektro-mágneses hullám körfrekvenciája, „f” pedig a frekvenciája. Egyszerű megfontolásokból a hullám terjedési sebessége k-val és  -val kifejezhető:
-val kifejezhető:
![\[{{c = \frac{\omega }{\left| \mathbf{k} \right|}}}\]](/images/math/4/9/8/498df15b96825a8a3056b81993690aaa.png)
A „k” helyett a gyakorlatban 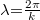 -t szokás használni, amelyet hullámhossznak nevezünk. Így az egyenlet ismertebb alakjában
-t szokás használni, amelyet hullámhossznak nevezünk. Így az egyenlet ismertebb alakjában 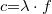 . Az (1) egyenletből látszik
. Az (1) egyenletből látszik  szemléletes jelentése is: azt a k vektor irányában mért legkisebb távolságot jelenti, amely szerint a térerősség periodikusan változik.
szemléletes jelentése is: azt a k vektor irányában mért legkisebb távolságot jelenti, amely szerint a térerősség periodikusan változik.
Doppler-effektus
Tegyük fel, hogy az (1) szerinti monokromatikus síkhullámot egy „K” koordináta-rendszerben írtuk fel. Ha ezt a síkhullámot a K-hoz képest v(t) pillanatnyi sebességgel mozgó K' rendszerből figyeljük, akkor a hullám K-beli frekvenciájától különböző frekvenciájú hullámot fogunk észlelni. Válasszuk úgy a K és K' rendszert, hogy -ban az origók egybe essenek. Ekkor a K-beli koordinátát K'-beli koordinátákkal kifejezhetjük:
![\[\mathbf{r} = \int\limits_0^t \mathbf{v}(\tau) d\tau + \mathbf{r'}\]](/images/math/7/2/9/7297839bfebf68cf6ad7ead6ea975e9d.png)
Ezt beírva az (1) egyenletbe, a hullám K'-beli alakját nyerjük:
![\[E\left( \mathbf{r'},t \right) = {E_0}\cos \left( \varphi (\mathbf{r'},t) \right)= {E_0}\cos \left( \omega t - \mathbf{k} \cdot \int\limits_0^t \mathbf{v}(\tau)d\tau - \mathbf{k} \cdot \mathbf{r'} \right)\]](/images/math/6/8/c/68c978c3caf0f4c63617e75ef88e46a4.png)
Definíció szerint a körfrekvencia a fázis (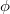 ) idő szerinti parciális deriváltja:
) idő szerinti parciális deriváltja:
![\[\omega '(t) \equiv \frac{\partial \varphi }{\partial t} = \omega - \mathbf{k} \cdot \mathbf{v}(t)\]](/images/math/6/6/d/66d73041d0097047380b492c5705ee09.png)
tehát a két rendszer relatív sebességétől függően a körfrekvencia megváltozik, mégpedig a két vonatkoztatási rendszer relatív sebességének pillanatnyi értéke szerint. (Az egyszerűség kedvéért v és ω időfüggését a továbbiakban nem jelöljük.) Ezt a jelenséget felfedezőjéről Doppler-effektusnak nevezik. A jelenség az akusztikában már XIX században ismert és igazolt volt. (A fenti eredmény csak közelítő jellegű, mivel a Galilei-féle relativitás elvének megfelelő transzformáció, amellyel az egyik koordináta rendszerből áttérünk a másikba, csak a fénysebességhez képest kis v sebességek esetében igaz. A pontos tárgyalásnál a Galilei-féle relativitást fel kell cserélni az Einstein-féle relativitás elvével és ennek megfelelően a két rendszer transzformációját Lorentz-transzformációval kell leírni, ld. a függeléket. A gyakorlatban szinte mindig teljesül az a feltétel, hogy v << c, ahol „c” a fénysebesség, ezért a kapott eredmények nagyon nagy pontossággal érvényben maradnak.) Felhasználva a
![\[k = \frac{2\pi }{\lambda } \qquad \omega = 2\pi f\]](/images/math/0/e/c/0ec87fbd72b4b725646ee7c79bcd9797.png)
egyenleteket, a körfrekvenciáról áttérve frekvenciára kapjuk:
![\[{{f' = f - \frac{\left| \mathbf{v} \right|}{\lambda }\cos \vartheta}}\]](/images/math/1/8/7/187e21043c83a83d4601cc0e608bd933.png)
ahol 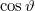 a k és v vektor által bezárt szög koszinusza. Speciálisan, ha k és v azonos irányú, akkor
a k és v vektor által bezárt szög koszinusza. Speciálisan, ha k és v azonos irányú, akkor 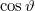 , így:
, így:
![\[{{f' = f - \frac{\left| \mathbf{v} \right|}{\lambda }}}\]](/images/math/2/9/1/291d690bfda0bad1dc4b297e4ae14de7.png)
és ha ellentétes irányúak, akkor 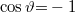 , melyből:
, melyből:
![\[{{f' = f + \frac{\left| \mathbf{v} \right|}{\lambda }}}\]](/images/math/6/b/9/6b9a4002dacd0e2a8f87f4767d843bff.png)
Optikai keverés
Tekintsünk két különböző frekvenciájú (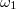 és
és 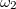 ), és azonos terjedési irányú (x) elektromágneses síkhullámot, ahol az egyik körfrekvencia időfüggő:
), és azonos terjedési irányú (x) elektromágneses síkhullámot, ahol az egyik körfrekvencia időfüggő: 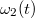 . Ebben az esetben az elektromos térerősségek a következőképp írhatók fel:
. Ebben az esetben az elektromos térerősségek a következőképp írhatók fel:
![\[{{{E_1} = {E_{10}}\cos \left( {{\omega _1}t - {k_1}x} \right)}}\]](/images/math/a/7/7/a7709a1c3886877b1eb5600faa6e9ef2.png)
![\[{E_2} = E_{20}\cos \left( \int\limits_0^t \omega _2(\tau )d\tau - \int\limits_t^{t - x/c} \omega _2(\tau )d\tau + \varphi \right)=E_{20}\cos \left( \int\limits_t^{t - x/c} \omega _2(\tau )d\tau + \varphi\right)\]](/images/math/5/7/f/57f8c6e3341e643188bc0c321c13db14.png)
ahol „c” a fénysebesség,  pedig egy konstans fázistolás. Az eredő elektromágneses tér a kettő összege:
pedig egy konstans fázistolás. Az eredő elektromágneses tér a kettő összege:
![\[E = E_1 + E_2 = E_{10}\cos \left(\omega_1t - k_1x\right) + E_{20}\cos\left(\int\limits_t^{t - x/c} \omega _2(\tau )d\tau + \varphi\right)\]](/images/math/d/e/0/de09a912c6b9ab90ae0abbb5c2dd4e5c.png)
Helyezzünk az eredő tér egy adott pontjába (x) fényérzékelőt. Az érzékelő által szolgáltatott áram 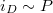 , ahol „P” a detektorra eső fényteljesítmény. A fényteljesítmény viszont az elektromos térerősség négyzetével arányos:
, ahol „P” a detektorra eső fényteljesítmény. A fényteljesítmény viszont az elektromos térerősség négyzetével arányos:
![\[P\sim E^2 = E_{10}^2 \cos^2\left(\omega_1t - k_1x\right) + E_{20}\cos^2\left(\int\limits_0^{t-x/c}\omega_2(\tau)d\tau + \varphi \right)+2E_{10}E_{20}\cos\left(\omega_1t - k_1x\right)\cos\left(\int\limits_{0}^{t-x/c}\omega_2(\tau)d\tau + \varphi\right)\]](/images/math/4/5/d/45d15020a51f96be9845137f137e1e15.png)
Ha ω2-t ω1-ből Doppler-eltolással állítjuk elő, és az alkalmazott sebességek nem relativisztikusak akkor ω2 csak nagyon kicsit tér el a konstans ω1-től. A továbbiakban egyszerűbb, ha az ω2 időfüggését egy külön 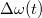 taggal kezeljük, amely jóval kisebb ω1-nél.
taggal kezeljük, amely jóval kisebb ω1-nél.
![\[\omega_2(t) = \omega_1 + \Delta\omega(t)\]](/images/math/d/a/8/da82eecfb18dc662befca584cf8ef16a.png)
Δω függését a koordinátarendszerek sebességétől lásd a következő fejezetben. Ekkor
![\[\int\limits_0^{t-x/c}\omega_2(\tau)d\tau = \omega_1(t-x/c) + \int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau\]](/images/math/3/7/d/37de04fd89f1253286612bc22946fafe.png)
Behelyettesítve (13)-ba a fenti összefüggést, és felhasználva, hogy
![\[{{\cos \alpha \cdot \cos \beta = \frac{1}{2}\left( {\cos \left( {\alpha + \beta } \right) + \cos \left( {\alpha - \beta } \right)} \right)}}\]](/images/math/e/d/e/edeb7e191965d71c4d6b7f0ef74cc12d.png)
iD alakja a következő:
![\[i_D \sim E_{10}^2\cos^2\left(\omega_1t - k_1x\right)+ E_{20}^2cos^2\left(\omega_1t - k_1x + \int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau - \varphi\right) + E_{10}E_{20}\cos\left[2\omega_1t - 2k_1x + \int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau + \varphi\right] + \]](/images/math/8/0/d/80d7e61d3371106f198b45043afc21a4.png)
![\[E_{10}E_{20}\cos\left[-\int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau - \varphi\right]\]](/images/math/1/3/6/1369728c41961da2c04d41d268e5f336.png)
A detektor a ráeső teljesítmény időátlagát méri. Mivel fény esetén 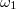 és
és 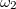 ~1015 nagyságrendű, és ezt a frekvenciát a fényérzékelő nem képes követni, az első három tag iD kifejezésében kiátlagolódik. Felhasználva, hogy:
~1015 nagyságrendű, és ezt a frekvenciát a fényérzékelő nem képes követni, az első három tag iD kifejezésében kiátlagolódik. Felhasználva, hogy:
![\[\left<\cos(x)\right> {{=}} 0\]](/images/math/d/0/2/d02ac06f22e163259bc590e80874612b.png)
![\[\left<\cos^2(x)\right> = \frac{1}{2}\]](/images/math/1/a/1/1a1ae1786360bfadec544cd7641c70a2.png)
![\[\cos(-x) {{=}} \cos(x)\]](/images/math/3/0/e/30e7fff53958b633533761ea8267c96d.png)
ahol < > az időátlagot jelenti. A detektor jelére azt kapjuk, hogy:
![\[\left<i_D\right> \sim \frac{E_{10}^2}{2} + \frac{E_{20}^2}{2} + E_{10}E_{20}\cdot\cos\left(\int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau + \varphi\right)\]](/images/math/3/2/d/32dda468ce8a4f9981fec391c147c5dd.png)
Az időátlagolást a fenti kifejezésben a fényhullám periódusidejének néhányszorosára végeztük el (ahogy a detektor is teszi), ezért ha 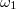 és
és 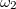 elég közel esik egymáshoz, a (17) kifejezés negyedik tagja átlagolás után is megmarad, ugyanis az
elég közel esik egymáshoz, a (17) kifejezés negyedik tagja átlagolás után is megmarad, ugyanis az 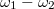 jóval nagyobb magánál
jóval nagyobb magánál 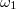 és
és 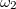 -nél. Amennyiben a különbségi körfrekvencia olyan kicsi, hogy az ebből eredő változást már a fényérzékelő is képes követni, a detektor kimenő jelében megjelenik egy, a két fény körfrekvencia-különbségével változó jel, melynek amplitúdója a két térerősség amplitúdójának szorzata. Bevezetve az intenzitásokra az
-nél. Amennyiben a különbségi körfrekvencia olyan kicsi, hogy az ebből eredő változást már a fényérzékelő is képes követni, a detektor kimenő jelében megjelenik egy, a két fény körfrekvencia-különbségével változó jel, melynek amplitúdója a két térerősség amplitúdójának szorzata. Bevezetve az intenzitásokra az 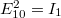 és
és 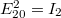 jelölést:
jelölést:
![\[\left<i_D\right> \sim \frac{I_1}{2} + \frac{I_2}{2} + \sqrt{I_1 I_2}\cdot\cos\left(\int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau + \varphi\right)\]](/images/math/b/2/2/b22748fb804647cfe4c20b37c714a209.png)
Az így kapott jel egyenáramú komponense a két fényhullám intenzitásának összegével arányos, ami e mérésben nem informatív, ezért elektronikus úton leszűrjük. A mért jel váltóáramú komponensét (iH) heterodin jelnek, az eljárást pedig heterodin keverésnek nevezzük:
![\[i_H \equiv \sqrt{I_1 I_2}\cdot\cos\left(\int\limits_0^{t-x/c}\Delta\omega(\tau)d\tau + \varphi\right)\]](/images/math/9/5/a/95ab0f5d9374e083f3becaf77f5a1648.png)
Az optikai keverésnél az intenzitások közül az egyiket elektromos analógia alapján lokáloszcillátornak nevezik (I1), a másikat pedig jelintenzitásnak (I2). Fénydetektálás szempontjából az optikai keverésnek azért van nagy jelentősége, mert a keletkező heterodin jel frekvenciája jól meghatározott értékű, valamint megfelelő nagyságú lokáloszcillátor-intenzitás segítségével a 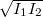 szorzat még kis I2 mellett is megnövelhető. Így az optikai keverés kis fényintenzitások mérésének egyik alkalmas módszereként kínálkozik. Ha például egy detektor érzékenysége 1 mW, és ennél kisebb jelet, mondjuk 10 μW-ot akarunk vele mérni, akkor a 10 μW-os jelet összekeverve egy 1 W-os lokál-oszcillátor jelével, akkor kb. 3 mW-os kevert jel keletkezik, amely már mérhető az adott detektorral. A dolog szépséghibája, hogy a detektoron megjelenik egy nagy, jelen esetben 1 W-os egyenáramú jel is, ami az érzékelőt, vagy az elekronikus erősítőt telítésbe viheti.
szorzat még kis I2 mellett is megnövelhető. Így az optikai keverés kis fényintenzitások mérésének egyik alkalmas módszereként kínálkozik. Ha például egy detektor érzékenysége 1 mW, és ennél kisebb jelet, mondjuk 10 μW-ot akarunk vele mérni, akkor a 10 μW-os jelet összekeverve egy 1 W-os lokál-oszcillátor jelével, akkor kb. 3 mW-os kevert jel keletkezik, amely már mérhető az adott detektorral. A dolog szépséghibája, hogy a detektoron megjelenik egy nagy, jelen esetben 1 W-os egyenáramú jel is, ami az érzékelőt, vagy az elekronikus erősítőt telítésbe viheti.
Optikai keverés megvalósítása Doppler-effektus felhasználásával
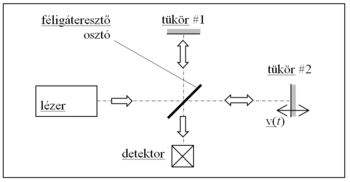
Az optikai keverés megvalósításához egy interferométerre van szükség. Az 1. ábrán látható Michelson-interferométerben a két nyaláb a karokból a féligáteresztő lemezen egyesül úgy, hogy a detektort azonos ponton találja el, és irányuk is pontosan megegyezik (azaz k1 és k2 párhuzamos).
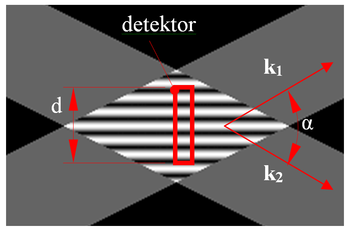
Ha ugyanis k1−k2-nek van a terjedési irányra merőleges komponense (α ≠ 0, ld. 2. ábra), a detektor síkjában egy interferencia csíkrendszer alakul ki, ami miatt a heterodin jel kiátlagolódhat. Azért, hogy ezt elkerüljük, a detektor méretének (d) kisebbnek kell lennie a kialakuló interferencia kép fél periódusánál:
![\[d < \frac{1}{4\cdot k_1\cdot \sin\left (\alpha/2\right )}\]](/images/math/e/0/f/e0ffc8d51aa55972d9735ffdf6ca00fd.png)
ahol felhasználtuk, hogy 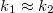 . Mivel a detektor mérete általában adott, az előző kifejezés a nyalábok egymáshoz viszonyított irányának beállítására ad egy erős kényszert: ha a detektor mérete d = 1 mm, λ = 633 nm, akkor α < 0,003°, ami 20 m-en 1 mm távolságnak felel meg!
. Mivel a detektor mérete általában adott, az előző kifejezés a nyalábok egymáshoz viszonyított irányának beállítására ad egy erős kényszert: ha a detektor mérete d = 1 mm, λ = 633 nm, akkor α < 0,003°, ami 20 m-en 1 mm távolságnak felel meg!
Az optikai keveréshez szükséges kismértékű frekvencia eltérést a Doppler-effektus révén érhetjük el: az interferométer egyik karjában lévő tükör (#2, ld. 1. ábra) önmagával párhuzamos, nyalábra merőleges, „v” sebességgel történő mozgatása esetén a tükörre eső fény frekvenciája a doppler effektus miatt megváltozik. A mozgó tükör az álló forrásból érkező „f” frekvenciájú lézernyalábot f'-nek érzékeli:
![\[f' = f - \frac{v}{\lambda}\]](/images/math/6/2/0/620606eeed058d89cb1e3d786ae8d007.png)
ahol a sebesség előjeles mennyiség (v > 0, ha a tükör a forrástól távolodik). A tükör ilyen frekvenciájú fényt ver vissza, azonban a detektor egy másik frekvenciát (f ) érzékel, ugyanis a tükör hozzá képest egy mozgó forrás. A mozgó tükör karjából érkező fény frekvenciája a detektornál tehát:
![\[f" = f' - \frac{v}{\lambda} = f - \frac{2v}{\lambda} \qquad \Leftrightarrow \qquad \omega_2 = \omega_1 - k_1 \cdot 2v\]](/images/math/d/e/a/dea9ab6f82dc24fd5f13b4f6f2a6f07e.png)
A frekvenciák közötti különbség tehát:
![\[\Delta \omega = -2\cdot k_1\cdot v\]](/images/math/7/d/0/7d0750956592d16e99f10479d8a1082c.png)
ahol 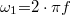 és
és 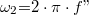 . Ebből a heterodin frekvencia:
. Ebből a heterodin frekvencia:
![\[f_H \equiv f' - f" = \frac{2\cdot v(t)}{\lambda}\]](/images/math/e/0/5/e057242996384012b08a6af6bd26199b.png)
A másik nyalábnak a frekvenciája változatlan, így a keletkező heterodin jel (21) szerint:
![\[i_H \equiv \sqrt{I_1I_2}\cdot \cos\left [\int\limits_0^{t-x/c}k_1\cdot 2v(\tau)d\tau - \varphi \right ]\]](/images/math/b/4/e/b4e086fd5131bc59b1d4eb3b876f85d1.png)
A sebesség időfüggése szempontjából két speciális esetet érdemes megvizsgálni. Az egyik az egyenes vonalú egyenletes sebességű mozgás. Ekkor v(t) = v = const., azaz (27) egyenletből az integrálás elvégzése után a következő marad:
![\[i_H \equiv \sqrt{I_1I_2}\cdot \cos \left [k_1\cdot 2v\cdot \left (t-\frac{x}{c}\right ) - \varphi \right ] = \sqrt{I_1I_2}\cdot \cos \left [(\omega_1 -\omega_2)\cdot t -(k_1 - k_2)\cdot x - \varphi\right ]\]](/images/math/0/f/e/0fee7e46857609dbfe48c66e85d53b21.png)
ahol felhasználtuk (24)-et. Egy lebegésszerű jelenséget tapasztalunk: a heterodin jel a körfek-venciák különbségének megfelelő frekvenciával harmonikusan változik. A másik jellemző sebességfüggést, a szinuszos rezgőmozgást végző tükröt, a következő alfejezetben tárgyaljuk.
Amplitúdó mérés heterodin méréstechnikával
Az előző fejezetben tárgyaltuk, hogy az interferométer egyik tükrének állandó, a tükörre merőleges sebességgel történő mozgatásának hatására milyen heterodin jel keletkezik és ez hogyan használható a sebesség nagyságának meghatározására. Ebben a fejezetben azt vizsgáljuk milyen a heterodin jel alakja, ha mozgás ugyan merőleges a tükörre, de a sebesség nagysága időben változó: a példa kedvéért harmonikus rezgőmozgás. A rezgés kitérése:
![\[x_r = x_0\cos (\omega_rt + \varphi_r)\]](/images/math/e/3/9/e395a30ab69fff47338f7f8d197c2770.png)
ahol 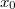 az amplitúdó
az amplitúdó 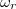 a rezgés körfrekvenciája
a rezgés körfrekvenciája 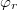 pedig a kezdőfázis. Ez alapján a pillanatnyi sebesség:
pedig a kezdőfázis. Ez alapján a pillanatnyi sebesség:
![\[v(t) = \dot{x} = -x_0\omega_r \sin (\omega_rt + \varphi_r)\]](/images/math/d/1/1/d11e834ff1300794f4df08fdf5f218ab.png)
A heterodin frekvencia pedig:
![\[f_H = \frac{2v}{\lambda} = -\frac{2x_0\omega_r\sin(\omega_rt+\varphi_r)}{\lambda}\]](/images/math/4/b/0/4b06a4aac362d23d1116d9f5d8cdd28c.png)
Itt „v” a tükör #2 sebessége az interferométerben,  az alkalmazott fény hullámhossza. A heterodin jel alakja a harmonikusan rezgő tükör esetén (27) és (30) alapján:
az alkalmazott fény hullámhossza. A heterodin jel alakja a harmonikusan rezgő tükör esetén (27) és (30) alapján:
![\[i_H \equiv \sqrt{I_1I_2}\cos \left [\int\limits_0^{t-x/c}k_1\cdot 2v(\tau)d\tau - \varphi \right ] = \sqrt{I_1I_2}\cos \left [k_1\cdot 2x_0\cdot \cos \left (\omega_r \cdot (t-x/c)+ \varphi_r\right ) - \varphi \right ]\]](/images/math/e/0/3/e03643337f53d0ecdac890e83bdd13ba.png)
ahol  -be a t = 0 miatt újonnan keletkezett konstans fázistolást is belevettük. Ha
-be a t = 0 miatt újonnan keletkezett konstans fázistolást is belevettük. Ha 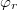 -be szintén beleértjük az x/c-ből eredő konstans fázistolást, akkor a heterodin jel alakja a következő:
-be szintén beleértjük az x/c-ből eredő konstans fázistolást, akkor a heterodin jel alakja a következő:
![\[i_H \equiv \sqrt{I_1I_2}\cos \left [k_1\cdot 2x_0\cdot \cos(\omega_rt + \varphi_r) -\varphi \right ]\]](/images/math/0/5/1/0510476fae5f581ad18143d9d0b3596d.png)
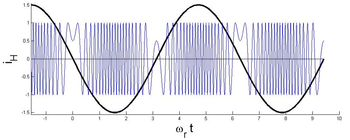
A 3. ábrán jól láthatóak a heterodin jel nullhelyei. Célunk az, hogy összefüggést találjunk az adott idő alatt mérhető nullátmenetek és a rezgés amplitúdója között. Vizsgáljuk meg mi a feltétele annak, hogy a heterodin jel értéke 0 legyen. Ha bevezetjük a heterodin jel fázisára a:
![\[\Phi \equiv k_1\cdot 2x_0\cdot \cos(\omega_rt + \varphi_r) - \varphi\]](/images/math/2/a/a/2aa7be11df94aaf3210e877deed986a9.png)
jelölést, akkor a zérus helyek feltétele:
![\[\cos(\Phi) = 0 \quad \to \quad \Phi = (2n+1)\frac{\pi}{2} \quad n \in Z\]](/images/math/6/f/1/6f1512158d8759b8cf23141686f78b3c.png)
Ebből a következő adódik:
![\[\Phi = \frac{4\pi x_0}{\lambda}\cos (\omega_rt + \varphi_r) - \varphi = (2n+1)\frac{\pi }{2}\]](/images/math/c/9/a/c9ac5a7189769dc46c005153d603ab61.png)
Vegyük a 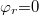 és
és 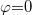 esetet, és vizsgáljuk meg hány nullahelye van a heterodin jelnek a rezgés egy félperiódusa alatt, azaz
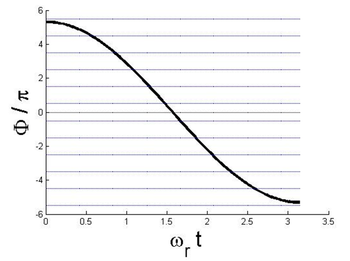
esetet, és vizsgáljuk meg hány nullahelye van a heterodin jelnek a rezgés egy félperiódusa alatt, azaz ![\setbox0\hbox{$\omega_rt \in [0;\pi]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/2/f/8/2f81679d6599eec4e1f230a065510fdc.png) intervallumon? A 4. ábra mutatja a
intervallumon? A 4. ábra mutatja a 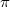 -vel normált fázist az idő függvényében; azt keressük, ez a görbe hol veszi fel a (36)-ban meghatározott értékeket (ld. vízszintes rácsozat).
-vel normált fázist az idő függvényében; azt keressük, ez a görbe hol veszi fel a (36)-ban meghatározott értékeket (ld. vízszintes rácsozat).
Az 4. ábra vízszintes rácsozata és a görbe metszéspontjai határozzák meg a heterodin jel nullátmeneteinek időpontjait. Egy fél periódus alatt a (36) függvény 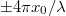 közötti értékeket vehet föl, a nullahelyek száma tehát:
közötti értékeket vehet föl, a nullahelyek száma tehát:
![\[N = 2\cdot Round\left ( \frac{4x_0}{\lambda}\right )\]](/images/math/b/7/3/b7328bae8a2f92deab3131654587ddca.png)
ahol Round(E) az „E” értékének matematikai szabályok szerinti kerekítése. Hogyha a 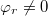 vagy
vagy 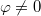 , akkor ezek és x0 pontos értékétől függően a nullhelyek értéke eltérhet a képlettől ± 2-vel. Általános esetben tehát, ha a kezdőfázisok ismeretlenek:
, akkor ezek és x0 pontos értékétől függően a nullhelyek értéke eltérhet a képlettől ± 2-vel. Általános esetben tehát, ha a kezdőfázisok ismeretlenek:
![\[N = 2\cdot Round\left ( \frac{4x_0}{\lambda}\right )\pm 2\]](/images/math/a/1/6/a16e7425611c203e7f7172abaf5cecb5.png)
A fázisok hatásának megértéséhez a nullhelyeket meghatározó (36) képletet átrendezzük:
![\[\frac{4\pi x_0}{\lambda}\cos (\omega_rt + \varphi_r) = (2n+1)\frac{\pi}{2} - \varphi\]](/images/math/b/5/f/b5f9a49cf63850211e985f0c3a511676.png)
Ez alapján úgy lehet képzelni, mintha  a 4. ábrán szereplő rácsozatot függőlegesen,
a 4. ábrán szereplő rácsozatot függőlegesen, 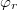 pedig az egész görbét vízszintesen tologatná. A kísérlet során a harmonikus rezgést egy hangfrekvenciás elektromos generátorral hozzuk létre és a nullahelyeket ezen gerjesztő jel félperiódusa alatt számoljuk meg, azonban a valódi rezgés ehhez képest
pedig az egész görbét vízszintesen tologatná. A kísérlet során a harmonikus rezgést egy hangfrekvenciás elektromos generátorral hozzuk létre és a nullahelyeket ezen gerjesztő jel félperiódusa alatt számoljuk meg, azonban a valódi rezgés ehhez képest 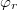 fázissal el van tolódva, ami az elektromos (kábelhossz, eszközök frekvencia átvitele) és a mechanikai fáziseltolódás összege. A mechanikai fázistolás a teljes heterodin jel időfüggő eltolódását okozza, az elektronikai rendszer fázistolása pedig a gerjesztő feszültséghez képest tolja el a rezgő tükör sebesség-idő függvényét. A
fázissal el van tolódva, ami az elektromos (kábelhossz, eszközök frekvencia átvitele) és a mechanikai fáziseltolódás összege. A mechanikai fázistolás a teljes heterodin jel időfüggő eltolódását okozza, az elektronikai rendszer fázistolása pedig a gerjesztő feszültséghez képest tolja el a rezgő tükör sebesség-idő függvényét. A  az optikai elemek fázistolásának, és mechanikai pozíciójának eredménye (hatására a heterodin jel kezdőfázisa változik meg a sebesség-időfüggvényhez képest), így az optikai elemek nagyon kicsi elmozdulásaira is igen nagyot változik: a rendszer a mechanikai rezgésekre igen érzékeny lesz.
az optikai elemek fázistolásának, és mechanikai pozíciójának eredménye (hatására a heterodin jel kezdőfázisa változik meg a sebesség-időfüggvényhez képest), így az optikai elemek nagyon kicsi elmozdulásaira is igen nagyot változik: a rendszer a mechanikai rezgésekre igen érzékeny lesz.
A mérést az 1. ábra szerinti interferométerrel végezzük el, amelyben természetesen csak akkor kapunk eredményt, ha x0 elég nagy. Amennyiben 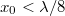 , akkor nullahelyek nem lépnek fel, így ez az eljárás nem alkalmazható. (Ekkor csak a heterodin jel spektrális vizsgálata adhat információt az amplitudóról.) Ezért a heterodin jel nullátmeneteinek számlálásával az alkalmazott lézerfény hullámhosszánál (
, akkor nullahelyek nem lépnek fel, így ez az eljárás nem alkalmazható. (Ekkor csak a heterodin jel spektrális vizsgálata adhat információt az amplitudóról.) Ezért a heterodin jel nullátmeneteinek számlálásával az alkalmazott lézerfény hullámhosszánál (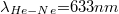 ) nagyobb amplitúdójú rezgéseket lehet csupán vizsgálni. Ha a nullátmenetek között eltelt idők reciprokát képezzük, akkor ezek úgy tekinthetők, mint a ti és ti+1 időpontok közötti pillanatnyi frekvencia, így ezen időközök
) nagyobb amplitúdójú rezgéseket lehet csupán vizsgálni. Ha a nullátmenetek között eltelt idők reciprokát képezzük, akkor ezek úgy tekinthetők, mint a ti és ti+1 időpontok közötti pillanatnyi frekvencia, így ezen időközök 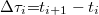 mérésével a pillanatnyi sebesség abszolút értéke is meghatározható az alábbi összefüggés alapján (de az előjele nem):
mérésével a pillanatnyi sebesség abszolút értéke is meghatározható az alábbi összefüggés alapján (de az előjele nem):
\[\frac{1}{2\Delta \tau_i} = (f_i) \sim \frac{2\]
Mérési feladatok
PDF formátum
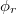 határozza meg a görbék együttes mozgását az időskálán,
határozza meg a görbék együttes mozgását az időskálán,