„Gázionizációs detektorok” változatai közötti eltérés
| 59. sor: | 59. sor: | ||
'''Gáz_03''' | '''Gáz_03''' | ||
| − | A Compton szórásban (4. ábra) a foton az atomból kilök egy elektront, és egy kisebb energiájú foton {is} továbbhalad A folyamatot leíró összefüggések: | + | A Compton szórásban (4. ábra) a foton az atomból kilök egy elektront, és egy kisebb energiájú foton {is} továbbhalad. A folyamatot leíró összefüggések: |
A Compton-elektron energiája: | A Compton-elektron energiája: | ||
| − | + | {| width = "100%" | |
| − | + | |- | |
| − | + | | width = "10%" | | |
| − | + | | width = "80%" | <div class="texdisplay"><latex display >\[ E_{c}=E_{\gamma}-E_{\gamma'} \]</latex></div> | |
| + | | align = "right" | <span id="eq2"> (2) </span> | ||
| + | |} | ||
A szórt foton energiája: | A szórt foton energiája: | ||
| − | + | {| width = "100%" | |
| − | + | |- | |
| − | + | | width = "10%" | | |
| − | + | | width = "80%" | <div class="texdisplay"><latex display >\[ E_{\gamma'} = \frac{E_{\gamma}}{E_{\gamma}(1-cos \vartheta)\diagup mc^{2}+1 } \]</latex></div> | |
| + | | align = "right" | <span id="eq2"> (2) </span> | ||
| + | |} | ||
| − | + | Ahol $m$ az elektron nyugalmi tömege, $c$ a fénysebesség, $\vartheta$ a szórás szöge (0$^{\circ}$ $\div$ 180$^{\circ}$). | |
a folyamat hatáskeresztmetszete: | a folyamat hatáskeresztmetszete: | ||
A lap 2013. március 18., 10:19-kori változata
Tartalomjegyzék[elrejtés] |
Bevezetés
A nukleáris méréstechnikában az egyik meghatározó detektor a GM-cső. Ennek oka az egyszerű felépítés, megbízhatóság és nem utolsó sorban a nagy (könnyen kezelhető) kimenő villamos jel.
Elméleti összefoglalás
Töltéshordozók keletkezése (ionizáció) töltött részecskéknél
Egy töltött részecske a gázokkal több módon léphet kölcsönhatásba. Detektálásra lényegében csak az elektromágneses kölcsönhatást használjuk fel, mivel e kölcsönhatás valószínűsége több nagyságrenddel meghaladja a többi kölcsönhatás valószínőségét. Az elektromágneses kölcsönhatásban legjelentősebb szerepe a belépő töltött részecske és a közeg elektromágneses tere közti Coulomb-kölcsönhatásnak van, amikor a közeg atomjai gerjesztődnek és ionizálódnak. A töltött részecske energiáját ütközések sorozata közben adja át. (A proton energiájának átlagosan mintegy 1/500, az alfa-részecske pedig csak kb. 1/2000 részét tudja átadni egy-egy ütközésben.)
Töltött-részecskék és anyag közötti kölcsönhatás
A sugárzások detektálásában leginkább a töltött részecskék és az anyag közötti elektromágneses kölcsönhatás érvényesül. A kölcsönhatás eredménye kisebb energiájú elektronok esetében elsősorban a targetmagok ionizációja, illetve gerjesztése, nagyobb energiák esetében pedig a detektálandó részecskéknek röntgensugárzással járó szóródása. Az előbbi mechanizmus játszik szerepet minden nehéz töltött részecskénél, továbbá olyan béta-részecskéknél, amelyek energiája 1 MeV-nél kisebb.
Gáz_01
Amikor valamilyen anyagon töltött részecskék haladnak keresztül, az atomok elektronjaival való ütközések sorozata következik be. Az elektronok kiütődhetnek az atomból, így keletkezik egy ion-pár, de az is előfordulhat, hogy az atom csak gerjesztődik, vagyis az elektronhéjon lévő egyik elektron magasabb energiájú állapotba kerül. Ez utóbbi esetben gerjesztett atomok keletkeznek (1. ábra).
Áthaladásuk során az alfa-részecskék nagy tömegükből és energiájukból adódóan gyakorlatilag egyenes nyomvonalon haladnak, nyomukban viszonylag széles és rövid ionizációs csatorna keletkezik. A béta-részecskék kis tömegükből adódó szóródási mechanizmusuk miatt hosszabb, cikcakkos úton, viszonylag gyérebb ionizációs csatornát eredményeznek (2. ábra).
Gáz_02
gamma-sugárzás és anyag kölcsönhatása
A gamma-sugárzás és az anyag közötti kölcsönhatás három alapvető formája a következő:
- fotoeffektus
- Compton-szórás
- párkeltés}
A gamma-sugárzás detektálása mindig e folyamatok valamelyikén alapul (lásd alább).
A fotoeffektusban (3. ábra) a foton abszorbeálódik, és az atomból egy elektront kilök. A következő összefüggések írhatók fel:
![\[ E_{f}=E_{\gamma}-E_{K} \]](/images/math/4/e/4/4e49e72d92cbf0ab5a7e34c9d4994868.png) |
(1) |
ahol 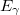 a gamma-foton energiája,
a gamma-foton energiája, 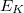 a fotoelektron kötési energiája az adott elektronhéjon
a fotoelektron kötési energiája az adott elektronhéjon
A folyamat hatáskeresztmetszete:
![\[ \mu_{f} \cong NZ^{5}(E_{\gamma})^{-3,5} \]](/images/math/d/c/6/dc62fea7f05484a0b0fe9f03581f9f5c.png) |
(2) |
Ahol  az anyag atomsűrűsége,
az anyag atomsűrűsége, 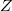 a rendszáma.
a rendszáma.
Gáz_03
A Compton szórásban (4. ábra) a foton az atomból kilök egy elektront, és egy kisebb energiájú foton {is} továbbhalad. A folyamatot leíró összefüggések:
A Compton-elektron energiája:
![\[ E_{c}=E_{\gamma}-E_{\gamma'} \]](/images/math/e/5/a/e5ad852cc555ec1a1d6e95da3e122c7f.png) |
(2) |
A szórt foton energiája:
![\[ E_{\gamma'} = \frac{E_{\gamma}}{E_{\gamma}(1-cos \vartheta)\diagup mc^{2}+1 } \]](/images/math/3/6/4/36456306a634fa43cd435116562ba4f9.png) |
(2) |
Ahol  az elektron nyugalmi tömege,
az elektron nyugalmi tömege,  a fénysebesség,
a fénysebesség, 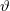 a szórás szöge (0
a szórás szöge (0
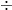 180
180 ).
).
a folyamat hatáskeresztmetszete:
\begin{equation}
\mu_{C} \cong {\frac{NZ}{E_{\gamma}}\textrm{ln} \Big(\frac{2E_{\gamma}}{mc^{2}}+\frac{1}{2} \Big) }
\label{eq_5}
\end{equation}
\begin{figure} [h]
\centering
\includegraphics[scale=0.30]{Gaztolt_04.PNG}
\caption{Compton-szórás}
\label{Gaztolt_04}
\end{figure}
E maximális, ha E
maximális, ha E minimális. Ez
minimális. Ez 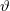 = 180
= 180 -nál következik be. Az ilyen szórási szögnek megfelelő E
-nál következik be. Az ilyen szórási szögnek megfelelő E -energiát a későbbiekben \textit{Compton}-élnek fogjuk nevezni.\\
-energiát a későbbiekben \textit{Compton}-élnek fogjuk nevezni.\\
A \textbf{párkeltés} folyamatában (5. ábra) a foton egy elektron-pozitron párt kelt egy atommal való kölcsönhatás során. Ez a reakció csak E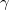
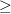 2mc
2mc = 1,022 MeV küszöbenergia fölött jöhet létre, ugyanis a folyamatban a
= 1,022 MeV küszöbenergia fölött jöhet létre, ugyanis a folyamatban a  -foton energiájának fedeznie kell az elektron-pozitron pár nyugalmi tömegét. Ha E
-foton energiájának fedeznie kell az elektron-pozitron pár nyugalmi tömegét. Ha E > 1,022 MeV, a többletenergia az elektron és pozitron mozgási energiájára fordítódik. A pozitron később egyesül egy elektronnal és két, közel 0,511 MeV energiájú
> 1,022 MeV, a többletenergia az elektron és pozitron mozgási energiájára fordítódik. A pozitron később egyesül egy elektronnal és két, közel 0,511 MeV energiájú  -foton jelenik meg. Ezt a reakciót nevezzük a pozitron annihilációjának
-foton jelenik meg. Ezt a reakciót nevezzük a pozitron annihilációjának
\begin{figure} [h]
\centering
\includegraphics[scale=0.30]{Gaztolt_05.PNG}
\caption{Párkeltés}
\label{Gaztolt_05}
\end{figure}
Mindhárom folyamat eredménye egy vagy több, jelentős energiával rendelkező elektron megjelenése. Ezek az elektronok azután a \textbf{Töltött-részecskék és anyag közötti kölcsönhatás} szakaszban leírt kölcsönhatásokban vesznek részt.
\subsubsection{Töltéshordozók mozgása elektromos térben (töltéshordozók viselkedése)}
Az ionizáció során keletkezett elektronok és ionok többszörös ütközés révén rövid idő alatt termikus egyensúlyba kerülnek a környező gázmolekulákkal. Az ionizáló részecske áthaladása után a töltéssel rendelkező részecskék a kamra elektródáira kapcsolt feszültség hatására mozogni kezdenek a gázon keresztül: az ionizációban keletkezett elektronok a pozitív elektróda (anód), a pozitív ionok pedig a negatív elektróda (katód) felé. Az ionok sebessége függ a kamra terében lévő elektromos térerősségtől, a kamrában lévő gáz nyomásától, valamint a gáz anyagi minőségétől. Az ionok leggyorsabban a könnyű gázokban haladnak (hidrogén, hélium), míg nehezebb gázokban lassan csökken a sebességük.
Nem minden ion és elektron jut el azonban a gyűjtő elektródáig, az alábbi okok miatt:
\begin{itemize}
\item \textit{Az elektron megkötődhet} a gázban, aminek a mértéke elsősorban az illető gáz természetétől függ. Az erősen elektronegatív elemek molekulái – oxigén és a halogének – elektronmegkötése igen erős, viszont a nemesgázoknak és a N , CH
, CH , H
, H molekuláknak egyáltalán nincs ilyen tulajdonságuk.
\item \textit{Rekombináció:} elektromos erőtér hatására az ellentétes irányba mozgó pozitív ionok és negatív elektronok (vagy pozitív és negatív ionok) egymással ütközve elveszíthetik töltésüket, egymást semlegesíthetik.
\end{itemize}
molekuláknak egyáltalán nincs ilyen tulajdonságuk.
\item \textit{Rekombináció:} elektromos erőtér hatására az ellentétes irányba mozgó pozitív ionok és negatív elektronok (vagy pozitív és negatív ionok) egymással ütközve elveszíthetik töltésüket, egymást semlegesíthetik.
\end{itemize}
Ha egy állandó sugárzásnak kitett ionizációs kamra jelét (áramát) vizsgáljuk az elektródáira kapcsolt feszültség függvényében, a 6. ábra szerinti karakterisztikát kapjuk. Az áram egy kezdeti gyors növekedés után állandó értékhez tart. Ezt az állandó, a kamra feszültségétől már nem függő áramot nevezzük az ionizációs kamra telítési jelamplitúdójának (áramának), azt a feszültséget pedig, amelynél az ionizációs kamra jele a telítési értéket eléri, telítési feszültségnek hívjuk. Egy ionizációs kamra telítési jelamplitúdóját akkor éri el, amikor az ionizációs folyamatban keletkezett összes töltéshordozó eljut a kamra gyűjtőelektródájára, mielőtt számottevő rekombinációs veszteség következne be.
\begin{figure} [h]
\centering
\includegraphics[scale=0.30]{Gaztolt_06.PNG}
\caption{Ionizációs kamra U/I karakterisztikája}
\label{Gaztolt_06}
\end{figure}
\subsection{Ionizációs kamrák}
Az ionizációs kamra (7. ábra) egy gázzal töltött edény, amelyben a két elektród között az ionizáló sugárzás által keltett töltéshordozók az elektromos térben való mozgásukkal áramot hoznak létre. Ha a keletkező jelet minden egyes ionizáló részecske esetében külön-külön mérjük, akkor a kamra impulzus üzemű. Ha a kamra jelének a kamrán átfolyó áram átlagát tekintjük, akkor áramüzemű (integráló) ionizációs kamráról beszélünk.
\begin{figure} [h]
\centering
\includegraphics[scale=0.30]{Gaztolt_07.PNG}
\caption{Az ionizációs kamra felépítése}
\label{Gaztolt_07}
\end{figure}
\subsubsection{Átlagárammérõ (integráló) ionizációs kamrák}
Ha az ionizációs kamrával nagy intenzitású sugárzást mérünk, az ionpárok repülési ideje alatt (a begyűjtési idő alatt) több új ionizáció következik be, és így az egyes ionizációs folyamatok már nem választhatók szét, ezért célszerű a kamrában létesített teljes ionizációs áram mérése (8. ábra).
Tekintve, hogy ez esetben az ionizációs áram nem függ a töltéshordozók tömegétől, az elektronmegkötés nem befolyásolja a kialakuló áram nagyságát. Ebből következik, hogy az ilyen kamráknál csaknem minden gáz használható, beleértve a levegőt is. Az ilyen kamrák áramának feszültségfüggése elhanyagolható, ha az elektródák feszültsége – a mérendő maximális intenzitású sugárzás esetén is – a telítési tartományban van (vö. 6. ábra).
Felépítésüket tekintve elterjedtek a henger, illetve síkkondenzátoros típusok. A kialakuló áramértékek gyakorlati nagyságrendje 10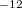 - 10
- 10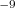 Amper.
Amper.
\begin{figure} [h]
\centering
\includegraphics[scale=0.30]{Gaztolt_08.PNG}
\caption{Ionizációs kamra integráló üzemmódban}
\label{Gaztolt_08}
\end{figure}
\subsubsection{Impulzus üzemű ionizációs kamrák}
Ha az ionizációs kamra áram- (vagy feszültség-) impulzusait tekintjük kimenetnek, impulzus üzemű kamráról beszélünk. A kapott jeleket megfelelő átvitelű erősítővel felerősítve használhatjuk számlálási, illetve spektroszkópiai célokra. Ma már csak speciális esetekben (\textit{ bórtöltésű}, illetve \textit{hasadási kamrák}) használják ezt, mivel egyéb típusú detektorok e téren előnyösebb tulajdonságokkal rendelkeznek (lásd alább).
\begin{figure} [h]
\centering
\includegraphics[scale=0.30]{Gaztolt_09.PNG}
\caption{Proporcionális számláló feszültség/áram karakterisztikája}
\label{Gaztolt_09}
\end{figure}
\subsection{Proporcionális számlálók}
Ha egy gázionizációs detektorban növeljük az elektródák feszültségét, azt tapasztaljuk, hogy a telítési szakasz utáni tartományban a kimenő jel növekedni kezd. (A 9. ábrán i = ionizációs tartomány, p = proporcionális tartomány). Ennek az a magyarázata, hogy kellő térerősség mellett az anód irányába vándorló elektronok a szabad úthosszon akkora energiára tesznek szert, hogy újabb ionizációt váltanak ki, ami töltéssokszorozást eredményez. Ezek az újabb elektronok azután maguk is ionizálnak mindaddig, míg az egész elektronlavina az anódszálba csapódik. Ez a \textit{ gázerősítés.} A gázerősítési tényező értéke függ a számlálócsőre kapcsolt feszültség nagyságától, az alkalmazott töltőgáz anyagi minőségétől, a gáz nyomásától és a cső geometriai méreteitől.
Az ilyen üzemmódban működő detektorokban minden primer ionpár, amelyet a detektálandó részecske kelt, azonos nagyságú elektronlavinát kelt. Ebből következik, hogy a kimenő elektromos impulzus az eredetileg keltett ionpárok számától, vagyis a detektálandó részecske által a detektor gáztérfogatában leadott energiával arányos. Erre való tekintettel az ilyen detektorokat proporcionális számlálóknak nevezzük. A 9. ábra szerint a proporcionális tartományban az arányossági tényező függ a detektorra adott U feszültségtől – mégpedig közel lineárisan. Ebből következik, hogy a detektor csak akkor tekinthető proporcionálisnak, ha az U feszültséget stabilizáljuk.
%\section{Ellenőrző kérdések}
%\begin{itemize}
%\item Ismertesse a neutron és anyag közötti kölcsönhatásokat.
%\item Ismertesse a BF töltésű proporcionális neutron-detektor működését.
%\item Ismertesse a
töltésű proporcionális neutron-detektor működését.
%\item Ismertesse a  He töltésű proporcionális neutron-detektor működését.
%\item Ismertesse a hasadási kamra működését.
%\item Ismertesse a kompenzált ionizációs kamra működését.
%\item Ismertesse a szcintillációs neutrondetektor működését.
%\end{itemize}
He töltésű proporcionális neutron-detektor működését.
%\item Ismertesse a hasadási kamra működését.
%\item Ismertesse a kompenzált ionizációs kamra működését.
%\item Ismertesse a szcintillációs neutrondetektor működését.
%\end{itemize}
%\begin{thebibliography}{9} %\bibitem{Kiss}Kiss D. Quittner P. Neutronfizika, Akadémiai Kiadó Budapest, 1971. %\bibitem{Kiss}Kiss D. Nagy Á. A neutronok szerepe a tudományban és a gyakorlatban, Akadémiai Kiadó Budapest ,1986. %\bibitem{Muhin}Muhin, K.N. Kisérleti magfizika, Tankönyv Kiadó Budapest, 1985. %\bibitem{Knoll}Knoll, Glenn F. Radiation detection and measurement, John Wiley \& Sons USA 1989. %\end{thebibliography}
\end{document}