„Vékonyréteg leválasztás” változatai közötti eltérés
(Új oldal, tartalma: „SZERKESZTÉS ALATT!!”) |
|||
| 1. sor: | 1. sor: | ||
SZERKESZTÉS ALATT!! | SZERKESZTÉS ALATT!! | ||
| + | |||
| + | == Vákuumpárologtatás / vákuumgőzölés == | ||
| + | |||
| + | A vákuumpárologtatás - vékonyrétegek előállítására szolgáló - fizikai gőzfázisú leválasztási eljárás (PVD, Physical Vapor Deposition). A leválasztani kívánt anyagot vákuumtérben - magas hőmérsékletre hevítve - elpárologtatják, majd az a bevonni kívánt munkadarab / hordozó / szubsztrát felületére lekondenzálva kialakítja a vékonyréteget. | ||
| + | |||
| + | === Fizikai elméleti alapok === | ||
| + | |||
| + | ==== Egyensúlyi telített gőznyomás ==== | ||
| + | <wlatex> | ||
| + | Egy zárt rendszerben 0 K-nél magasabb, állandó T hőmérsékleten az anyag felületéről kilépő és a felületre visszatérő atomok dinamikus egyensúlyban vannak, melyet az adott hőmérséklethez tartozó P egyensúlyi telített gőznyomással (tenzióval) jellemezhetünk. Az egykomponensű rendszer két fázisának egyensúlyi feltételét a Clausius-Clapeyron egyenlet adja meg: | ||
| + | |||
| + | {{NumBlk||$$ \frac{dp}{dT}=\frac{L_m}{T{\Delta}V_m} $$|1}} | ||
| + | |||
| + | ahol $L_m$ a fázisátalakuláshoz szükséges moláris hőmennyiség, ${\Delta}V_m$ pedig a két fázis móltérfogatának különbsége $(V_m^I-V_m^{II})$. | ||
| + | |||
| + | Szilárd-gőz fázisátalakulás esetén a szilárd fázis moláris térfogata $(V_m^{II})$ elhanyagolható a gőz fázis moláris térfogata $(V_m^I)$ mellett, így a ${\Delta}V_m{\cong}V_m^I=RT/P$ (R: az egyetemes gázállandó) összefüggést az {{EquationNote|1}} egyenletbe behelyettesítve az alábbi összefüggést kapjuk: | ||
| + | |||
| + | |||
| + | |||
| + | </wlatex> | ||
A lap 2013. március 24., 12:30-kori változata
SZERKESZTÉS ALATT!!
Vákuumpárologtatás / vákuumgőzölés
A vákuumpárologtatás - vékonyrétegek előállítására szolgáló - fizikai gőzfázisú leválasztási eljárás (PVD, Physical Vapor Deposition). A leválasztani kívánt anyagot vákuumtérben - magas hőmérsékletre hevítve - elpárologtatják, majd az a bevonni kívánt munkadarab / hordozó / szubsztrát felületére lekondenzálva kialakítja a vékonyréteget.
Fizikai elméleti alapok
Egyensúlyi telített gőznyomás
Egy zárt rendszerben 0 K-nél magasabb, állandó T hőmérsékleten az anyag felületéről kilépő és a felületre visszatérő atomok dinamikus egyensúlyban vannak, melyet az adott hőmérséklethez tartozó P egyensúlyi telített gőznyomással (tenzióval) jellemezhetünk. Az egykomponensű rendszer két fázisának egyensúlyi feltételét a Clausius-Clapeyron egyenlet adja meg:
ahol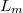 
a fázisátalakuláshoz szükséges moláris hőmennyiség, 
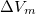pedig a két fázis móltérfogatának különbsége 
.
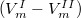Szilárd-gőz fázisátalakulás esetén a szilárd fázis moláris térfogata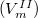 
elhanyagolható a gőz fázis moláris térfogata 
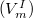mellett, így a 
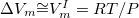(R: az egyetemes gázállandó) összefüggést az Sablon:EquationNote egyenletbe behelyettesítve az alábbi összefüggést kapjuk:
