„Transzport nanovezetékekben: Landauer-formula, vezetőképesség-kvantálás” változatai közötti eltérés
| 3. sor: | 3. sor: | ||
Makroszkopikus vezetékek ellenállása jól leírható az Ohm-törvénnyel: az áramsűrűség a fajlagos vezetőképesség és az elektromos tér szorzata, a vezetőképesség pedig arányos a vezeték keresztmetszettel és fordítottan arányos a hosszával: | Makroszkopikus vezetékek ellenállása jól leírható az Ohm-törvénnyel: az áramsűrűség a fajlagos vezetőképesség és az elektromos tér szorzata, a vezetőképesség pedig arányos a vezeték keresztmetszettel és fordítottan arányos a hosszával: | ||
$$\vec{j}=\sigma \cdot \vec{E}, \ \ \ G=R^{-1}=\frac{A\cdot \sigma}{L}$$ | $$\vec{j}=\sigma \cdot \vec{E}, \ \ \ G=R^{-1}=\frac{A\cdot \sigma}{L}$$ | ||
| + | Az Ohm törvény egyszerűen magyarázható az elektromos vezetés Drude modelljével. Az elektronok a kristályrácsban két ütközés közötti | ||
| + | $\tau_m$ karakterisztikus idő alatt $p_\mathrm{drift}=nm_\mathrm{drift}=eE\tau_m$ impulzust nyernek, majd a véletlen irányba történő szóródás hatására ezt elveszítik. : az elektromos tértől | ||
| + | |||
</wlatex> | </wlatex> | ||
== Kvantumvezeték ellenállása == | == Kvantumvezeték ellenállása == | ||
A lap 2013. április 27., 05:35-kori változata
Egy nanométeres skálájú objektum vezetési tulajdonságai több szempontból eltérnek a makroszkopikus skálán megszokott jelenségektől.
Makroszkopikus vezetékek ellenállása jól leírható az Ohm-törvénnyel: az áramsűrűség a fajlagos vezetőképesség és az elektromos tér szorzata, a vezetőképesség pedig arányos a vezeték keresztmetszettel és fordítottan arányos a hosszával:
![\[\vec{j}=\sigma \cdot \vec{E}, \ \ \ G=R^{-1}=\frac{A\cdot \sigma}{L}\]](/images/math/7/b/c/7bc09554c31016e9d495c03164518ac1.png)
Az Ohm törvény egyszerűen magyarázható az elektromos vezetés Drude modelljével. Az elektronok a kristályrácsban két ütközés közötti
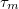karakterisztikus idő alatt 
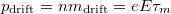impulzust nyernek, majd a véletlen irányba történő szóródás hatására ezt elveszítik. : az elektromos tértől
Kvantumvezeték ellenállása
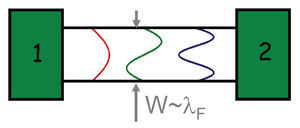
Egy hullámhosszal összemérhető szélességű, hosszú egyenes 2D kvantumvezetékben az elektronok hullámfüggvénye "hard wall" határfeltétellel:
![\[\Psi_{n,k}(x,y)=exp(i k x)\cdot sin\left(\frac{n \pi y}{W} \right)\]](/images/math/b/3/4/b343d66ae4c8640b900440d9fbce0499.png)
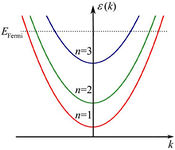
![\[\epsilon_n(k)=\frac{\hbar^2k^2}{2 m} + \frac{\pi^2 \hbar^2}{2 m W^2}\cdot n^2\]](/images/math/2/e/e/2eea1145eb1f05e5914cd5c4584a1028.png)
- X irányban: síkhullám terjedés
- Y irányban kvantált keresztmódusok
Diszperzós reláció
Diszperzós reláció a mintára feszültséget kapcsolva
- A különböző keresztmódusokhoz tartozó 1D parabolikus diszperziók: vezetési csatornák
- Fermi energiát metsző diszperziók: nyitott csatornák
- Ha feszültséget adunk a két elektróda közé akkor a bal oldali elektródából jövő állapotok (
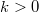) eV-al magasabb energiáig lesznek betöltve mint a jobb oldali elektródából jövők (
)
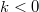Egy vezetési csatornában folyó áram:
![\[I^+=\frac{2 e}{L} \sum \limits_{k>0} v_k f_1(\epsilon_k) = 2e \int \frac{\mathrm{d}k}{2 \pi}\frac{\partial \epsilon_k}{\hbar \partial k} f_1(\epsilon_k) = \frac{2 e}{h}\int \mathrm{d} \epsilon f_1(\epsilon)\]](/images/math/a/4/9/a497c44ad3125b4c10a00aaeab36791d.png)
![\[I^-=\frac{2 e}{L} \sum \limits_{k<0} v_k f_2(\epsilon_k) = \frac{2 e}{h}\int \mathrm{d} \epsilon f_2(\epsilon)\]](/images/math/b/8/7/b87d522cfc4351134078079e018a0ea1.png)
![\[I=I^+-I^-=\frac{2 e}{h} \int \mathrm{d} \epsilon (f_1(\epsilon)-f_2(\epsilon))=\frac{2 e}{h}e V, \;\; G_0=\frac{2 e^2}{h}\]](/images/math/b/7/0/b70d7a4211cfca891b2d400f32e41ca2.png)
A csatornák nem tudnak egymásba átszóródni, mert ez sértené az impulzusmegmaradást, így függetlennek tekinthetjük őket.
![\[G=\frac{2 e^2}{h}M\]](/images/math/f/6/7/f67d1475647b7726064d42411b5fd018.png)
Landauer formula
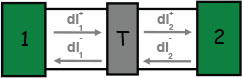
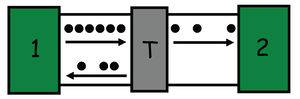
Egycsatornás vezeték egy szórócentrummal
![\[\mathrm{d}I_1^+(\epsilon)=\frac{2 e}{h}\cdot f_1(\epsilon)\mathrm{d}\epsilon,\;\; \mathrm{d}I_2^-(\epsilon)=\frac{2 e}{h}\cdot f_2(\epsilon)\mathrm{d}\epsilon\]](/images/math/3/6/0/360b61e98226c02a1e1a16361bc58a21.png)
![\[\mathrm{d}I_1^-(\epsilon)=\mathrm{d}I_1^+(\epsilon)\cdot (1-T) + \mathrm{d}I_2^-(\epsilon)\cdot T,\;\; \mathrm{d}I_1=\mathrm{d}I_1^+ - \mathrm{d}I_1^- = \frac{2 e}{h} \cdot T \cdot [f_1(\epsilon)-f_2(\epsilon)]\mathrm{d}\epsilon\]](/images/math/8/d/2/8d224e5a7b9878f0ddc04fc422fcf077.png)
![\[I=\int \mathrm{d}I_1(\epsilon) = \frac{2 e}{h} \cdot \int T\cdot [f_1(\epsilon)-f_2(\epsilon)]\mathrm{d}\epsilon = \frac{2 e}{h}\cdot eV \cdot T\]](/images/math/4/f/f/4ff1f321fb16436b7433ccce4d6866c1.png)
![\[G=\frac{2 e^2}{h}\cdot T\]](/images/math/d/0/5/d052002c8c3377f0262ad9bdf8595b64.png)
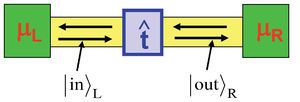
Két ideális kvantumvezeték kvantált keresztmódusokkal, köztük egy 
transzmissziós mátrix-szal leírható keskeny csatorna:
![\[|out \rangle_R = \hat{t} |in \rangle_L\]](/images/math/b/4/f/b4f6cb71c7ccbe78c04f1f1a03e2a1d5.png)
A vezetőképességet a Landauer formula adja meg:
![\[G = \frac{2 e^2}{h} \mathrm{Tr}(\hat{t}^\dagger \hat{t}) = \frac{2 e^2}{h} \sum \limits_{i=1..N} T_i\]](/images/math/e/e/7/ee72cf7c8a308ecb13d30d9a9a07c008.png)
- Megfelelő sajátbázisban a vezetőképesség transzmissziós sajátértékek összege, ún. „mezoszkópikus PIN kód”.
Az elektronok részecsketermészete 
"sörét" zaj
- Áram mérésekor vagy teljesen transzmittált, vagy teljesen reflektált elektront detektálunk, "fél" elektront soha.
- Időegység alatt transzmittált elektronok számának várható értéke:
![\[\langle N \rangle \sim G \sim T\]](/images/math/c/0/2/c02d8f3c3fedcbd4abe992ae84d2f314.png)
de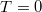 
vagy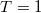 
kivételével véges szórást is tapasztalunk:
![\[\langle(N-\langle N \rangle)^2\rangle \sim T\cdot(1-T)\]](/images/math/3/d/b/3db6d0bbfe5c8a790206ab3cde4574c2.png)
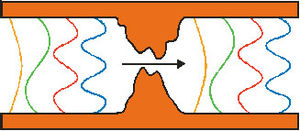
Vezetőképesség kvantálás kvantum pont-kontaktusban
Kvantum pont-kontaktus: két elektródát egy keskeny, hullámhosszal összemérhető szélességű csatorna köt össze, melynek a szélességét középen egy kapuelektródára tett feszültséggel változtathatjuk.
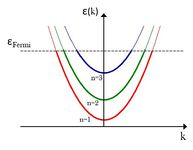
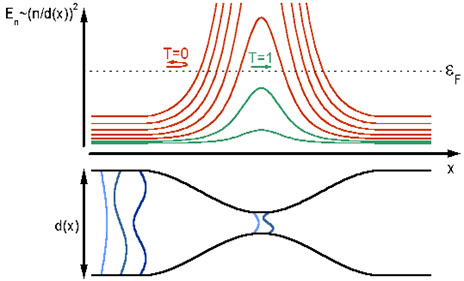
- A kontaktus közepe felé haladva ez elektron keresztirányú energiája nő, hosszirányú kinetikus energiája pedig csökken.
- Adiabatikusan változó csatornaszélességnél a csatornák nem tudnak egymásba szóródni, függetlennek tekinthetők.
- A kontaktus közepénél a legtöbb csatorna keresztirányú energiája nagyobb mint a Fermi energia, ezek a módusok visszaverődnek a kontaktusról.
- A kontaktus közepén is nyitott csatornák T=1 valószínűséggel átjutnak, hiszen a visszaverődés jelentős impulzusváltozással járna.
Nyitott csatornák száma a kontaktus közepén:
![\[G=\frac{2 e^2}{h}N_c\]](/images/math/c/0/9/c097a47ee67bd5df52de92a9c84d8949.png)
Vezetőképesség kvantálás!
