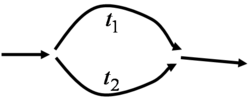Interferencia és dekoherencia nanoszerkezetekben
Tartalomjegyzék |
Interferencia-kísérletek hat nagyságrenddel kisebb skálán
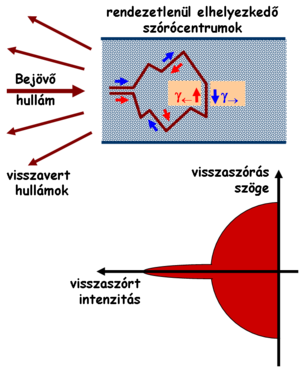
A fizikában régóta ismertek az interferencia-kísérletek, melyeknek egy emblematikus példája az 1. ábrán szemléltetett kétrés kísérlet. Ha fény két közeli résen halad keresztül, a rések mögé helyezett ernyőn interferencia-képet látunk, azaz az ernyőn látható intenzitásprofil nem egyezik meg az egyik illetve a másik rés kitakarásakor kapott intenzitások összegével, hanem azon tartományokban, ahova a két résen keresztül azonos fázissal érkezik a hullám erősítést, ahol pedig ellentétes (180 fokkal eltolt) fázissal, ott kioltást tapasztalunk. Természetesen ugyanez a jelenség a legkülönbözőbb közegekben megfigyelhető a vízhullámoktól a hanghullámokig.
 |
| 1. ábra. Kétrés kísérlet fénnyel |
A modern fizika fejlődésével az interferencia-kísérletek újabb értelmezést kaptak, hiszen jól demonstrálták a részecske hullám dualitást. Ha az 1. ábrán szemléltetett kísérletben nagyon kis fényintenzitást, és nagyon érzékeny ernyőt használunk, akkor először véletlenszerű felvillanásokat látunk az ernyő különböző pontjain, mely a fény részecske-természetét támasztja alá. Ha viszont sokat várunk, akkor a véletlenszerű felvillanásokból kirajzolódik a jól ismert interferencia-kép (lásd 2. ábra).
  |
| 2. ábra. Interferencia-kép kialakulása egyedi fotonbecsapódásokból |
További érdekesség, hogy ha a két rés mellé detektorokat helyezünk, és próbáljuk megállapítani, hogy a fényt alkotó fotonok éppen melyik résen haladnak keresztül, akkor azt tapasztaljuk, hogy minél pontosabban detektáljuk a résen áthaladó fotonokat, annál inkább elvész az interferenciakép. Azaz akár egyetlen foton is képes mindkét résen áthaladva önmagával interferálni, viszont ha megmérjük, hogy merre ment a foton, akkor az interferencia megszűnik.
Az elmúlt évtizedekben a nanofizika fejlődésének köszönhetően a kétrés kísérlethez hasonlóan izgalmas interferencia-kísérleteket mintegy 6 nagyságrenddel kisebb méretskálájú nanoáramkörökben is sikerült megvalósítani, ebbe a témakörbe nyújtunk betekintést a következőkben.
Fáziskoherencia-hossz
A nanovezetékek tárgyalásánál már említettük, hogy egy nanoáramkörben akkor tapasztalhatunk interferencia-jelenséget, ha annak mérete kisebb a fáziskoferencia-hossznál. Próbáljuk ezt a karakterisztikus méretskálát egy kicsit pontosabban definiálni.
 |
| 3. ábra. |
Ha egy elektronhullámot egy adott pontban szétválasztunk, és feltételezzük, hogy a két parciális hullám két különböző trajektórián keresztül jut el egy másik pontba, ahol újra egyesülnek (3. ábra), akkor ebben a pontban a hullám intenzitását
![\[ T=\left| t_1 \right|^2 + \left| t_2 \right|^2 + 2\left| t_1t_2 \right| \exp\left(-\tau_L/\tau_\phi \right) \]](/images/math/f/6/a/f6a8b87e66906c90851884c0ff20b7cf.png)
alakban írhatjuk, ahol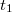 
és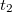 
az egyik illetve a másik trajektóriához tartozó komplex amplitúdó, 
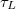pedig az egyik pontból a másik pontba történő eljutáshoz szükséges karakterisztikus idő.
A két trajektória mentén az elektronok szóródásokat szenvednek. Rugalmas (pl. rácshibákon, szennyezőkön, történő) szóródás esetén egy időben konstans fázistolás lép fel, de ez nem befolyásolja az interferencia-képességet, legfeljebb azt, hogy a parciális hullámok találkozásakor erősítést vagy gyengítést tapasztalunk. Ha viszont az elektronhullám az egyik trajektória mentén egy rugalmatlan szórást szenved (pl. elektron-fonon kölcsönhatás), akkor megváltozik az energiája, és így a hullámok egyesítésekor egy időben fluktuáló, kiátlagolódó interferenciaképet kapunk. A fenti képletben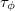 
ezen, rugalmatlan szórásoknak köszönhető koherenciavesztés karakterisztikus időskáláját adja meg. Ennél az időnél lényegesen hosszabb skálán a parciális hullámok egyesítésekor egyszerűen az intenzitások adódnak össze, és a fázisviszonyoktól függő interferenciatag (a fenti képlet utolsó tagja) elvész.
Ha két rugalmatlan szórás között nem történik rugalmas szórás, azaz 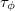összemérhető a momentum relaxáció 
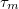karakterisztikus idejével, akkor az a távolságskála melyen belül interferenciát tapasztalunk egyszerűen
![\[ L_\phi=v_F \tau_\phi, \]](/images/math/5/b/1/5b1cc8b400baa30c186587a5876ca6f2.png)
ahol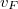 
az elektronok Fermi-sebessége. Ha viszont két rugalmatlan ütközés között számos rugalmas ütközés történik, akkor az elektronok diffúzív trajektóriák mentén mozognak. Ebben az esetben is 
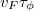trajektóriahossz után vész el az interferencia-készség, azonban ez a trajektóriahossz a diffúzív mozgás miatt térben csak
![\[ L_\phi=\sqrt{D\tau_\phi} \]](/images/math/9/d/b/9db6bbcb661635db0339040855f4a391.png)
eltávolodást eredményez a kiindulási ponttól, ahol 
a diffúziós állandó, mely a momentumrelaxációs időből két dimenzióban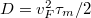 
képlettel számolható.
Aharonov-Bohm gyűrű
Nanoáramkörökben az interferencia-jelenségeket nem tudjuk a ernyő mentén detektálni, olyan elrendezést kell találni, melyben például az áramkör két (vagy pár) kontaktusán keresztül feszültséget adunk a mintára, és a mért áramban jelenik meg az interfernecia valamilyen hangolható paraméter függvényében. Erre talán a legjobb példa a nanogyűrűkben tapasztalható Aharonov-Bohm jelenség.
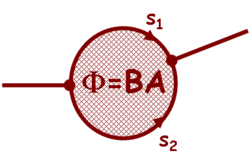
Az egyik kontaktusból bejövő elektronhullámot egy kör alakú gyűrű két ága mentén két részre osztjuk, és a gyűrű másik oldalára helyezett kontaktuson keresztül egyesül a két parciális hullám (4. ábra). Zérus mágneses térben az elektronok a felső ágon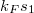 
, míg az alsó ágon 
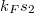fázist vesznek fel, ahol 
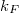a Fermi-hullámszám, 
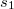és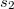 
pedig a két kontaktus közötti trajektóriahossz a felső illetve az alsó ág mentén (lásd 4. ábra). Ennek megfelelően az interferenciatag 
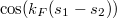-vel arányos.
 |
| 4. ábra Aharonov-Bohm gyűrű. |
Véges mágneses térben azonban a fenti fázisok mellett az elektronok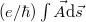 
ún. Aharonov-Bohm fázist is felvesznek, ahol 
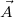a vektorpotenciál, az integrálást pedig az elektronok trajektóriája mentén kell elvégezni.
A gyűrű felső és alsó ágának járulékát összegezve:
![\[G\sim T = |t_1+t_2|^2 = \left| e^{i k_F s_1 + \frac{i e}{\hbar} \int \limits_1 \vec{A} \mathrm{d}\vec{s}} + e^{i k_F s_2 + \frac{i e}{\hbar} \int \limits_2 \vec{A} \mathrm{d}\vec{s}}\right|^2 = \]](/images/math/2/0/4/204d955f1a257147132a6d3acdd6939d.png)
![\[2+2\cdot cos\left(k_F(s_1-s_2)+\frac{e}{\hbar} \oint \vec{A} \mathrm{d} \vec{s}\right) = 2+2\cdot cos(\delta_0 + 2 \pi \Phi/\Phi_0),\]](/images/math/3/3/a/33aedd1e7cf2375923f620aefd44960c.png)
ahol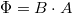 
a gyűrű által körbezárt mágneses fluxus, 
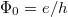pedig az úgynevezett fluxuskvantum. Látszik, hogy a vezetőképesség a fluxus változtatásával a fluxuskvantum periódusa szerint oszcillál. Ezt az oszcillációt először Webb és társai mutatták ki mezoszkopikus arany gyűrűn.1
A 4. ábrán szándékosan különbözőnek jelöltük a felső és alsó ág hosszát, hiszen egy valós rendszerben nem lehet garantálni, hogy mindkét ág mentén pontosan ugyan olyan hosszú trajektória mentén haladjanak az elektronok. Ráadásul, ha a gyűrű két ága egy-egy szélesebb vezeték, akkor mindkét ágon több, különböző hosszúságú trajektória mentén juthat el az elektron az egyik kontaktusból a másikba, és ha ezek a trajektórahosszok túlzottan eltérnek, akkor a szabad elektron terjedésből adódó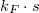 
fázisok kiátlagolódnak, a koherencia elvész.
Tanulságos az Aharonov-Bohm gyűrűben reflexiót számolva megnézni a releváns folyamatokat. A legalapvetőbb (nulladrendű) folyamat, ha az elektronok be se jutnak a gyűrűbe, hanem a gyűrű elején reflektálódnak (5. ábra, bal oldal). A következő, első rendben az elektronok úgy tudnak reflektálódni, hogy bejutnak a gyűrűbe, és jobbról vagy balról egyszer megkerülik azt, majd a bal oldali kontaktuson keresztül elhagyják a gyűrűt (5. ábra, középső és jobb oldali panel). Az Aharonov-Bohm effektus a nulladrendű, illetve az elsőrendű folyamatok interferenciájából adódik, melyek között a mágneses térből felvett fázis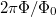 
. Azonban széles vezetékek esetén a 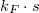fázisok kiátlagolódnak.
 |
| 5. ábra. Reflexióhoz járulékot adó alapvető folyamatok Aharonov-Bohm gyűrűben |
Érdemes megvizsgálni, a két elsőrendű folyamat interferenciáját, azaz amikor az elektronok balról illetve jobbról kerülik a gyűrűt. E két folyamat között a mágneses tér hatására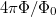 
fáziskülönbség lép fel, azaz a vezetőképesség a fluxuskvantum fele szerinti periódussal oszcillál. Két tetszőleges trajektória közötti 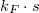fázisok itt is kiátlagolódhatnak, azonban minden egyes balról kerülő trajektóriához találunk egy időtükrözött jobbról kerülő trajektóriát, azaz egy trajektóriapárt, melyen pontosan ugyan azon a trajektórián, de ellentétes irányban halad az elektron. Az időtükrözött trajektóriapárok között a 
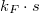fázisok különbsége pontosan zérus, így nulla mágneses térben mindig konstruktív interferenciát látunk, illetve véges mágneses térben a fluxuskvantum felének periódusával oszcillál a vezetőképesség. Ezt hívják Altshuler-Aronov-Spivak oszcillációnak.
 |
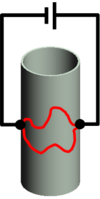
| 6. ábra. Altshuler-Aronov-Spivak oszcillációk hosszú, de kis átmérőjű fémhengerben is megfigyelhetők |
Az időtükrözött párok interferencia-járuléka vastag vezetékek esetén sem átlagolódik ki. Erre a legjobb példa Sharvin és Sharvin eredeti kísérlete, melyben egy kis átmérőjű (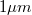
) szigetelő drótra vékony magnéziumréteget vittek fel, és a drót két oldala között mértek vezetőképességet (6. ábra). Ebben az elrendezésben nyilvánvaló, hogy az elektronok teljesen különböző hosszúságú trajektóriák mentén juthatnak el ez egyik kontaktusból a másikra, így a 
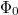periódusú Aharonov-Bohm oszcillációk kiátlagolódnak. Ezzel szemben az időtükrözött trajektóriák interferenciájából adódó 
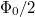periódusú Altshuler-Aronov-Spivak oszcillációk megmaradnak, és kísérletileg is kimutathatók, lásd A.G.Aronov és Yu.V.Sharvin összefoglaló cikke, 7. ábra. 2
Vezetőképesség-fluktuációk
Említettük, hogy túl széles vezetékkel készített Aharonov-Bohm gyűrűben a 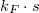fázisok kiátlagolódnak. Ez volt az oka annak, hogy az első próbálkozások Aharonov-Bohm oszcillációk kimutatására nanoszerkezetekben nem sikerültek, illetve a periodikus oszcillációk helyett a vezetőképesség a mágneses tér függvényében egy véletlenszerű fluktuációt mutatott. Később kiderült, hogy a vezetőképesség fluktuációja nanoszerkezetekben egy általános interferencia-jelenség.
 |
| 7. ábra. Vezetőképesség-fluktuációk |
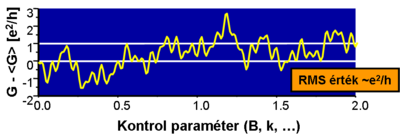
Egy megfelelő szélességű és hosszúságú (a momentumrelaxációs szabadúthossznál hosszabb, de a fáziskoherencia hossznál rövidebb) nanovezetékben az elektronok számtalan különböző diffúzív trajketória mentén juthatnak el az egyik kontaktusból a másikba (8. ábra). A kis méret miatt (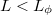
) ezek a diffúzív trajektóriák interferálnak egymással. A mágneses térrel hangolhatjuk az egyes trajektóriákhoz tartozó fázist, így változtathatjuk az interferenciafeltételeket, de mivel nagyon sok véletlen trajektória interferenciajárulékáról van szó, ezért a mágneses tér függvényében a vezetőképesség nem periodikus oszcillációt, hanem egy véletlenszerű fluktuációt mutat (lásd 9. ábra). Fontos azonban megjegyezni, hogy ha a mágneses teret oda-vissza változtatjuk, akkor ez a véletlenszerű vezetőképesség-fluktuáció pontosan reprodukál, hiszen a vezetéken belül a mérés során nem változik a szórócentrumok helye, így a sok trajektória interferenciájából adódó vezetőképesség-korrekció a mágneses tér egyértelmű függvénye. Ha viszont felmelegítjük, és újra lehűtjük a nanovezetéket, akkor a rácshibák pozíciója megváltozik, és így jellegre hasonló, de a részletekben a korábbitól teljesen eltérő vezetőképesség fluktuációt kapunk a mágneses tér függvényében.
 |
| 9. ábra. Vezetőképesség fluktuációk |
Megmutatható, hogy sok nyitott vezetési csatornával rendelkező (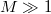
), diffúzív (
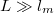) de még fáziskoherens (
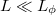) nanovezetékben a vezetőképesség-fluktuációk nagysága univerzális, a fluktuációk szórása a vezetőképesség értékétől függetlenül 
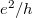(lásd 9. ábra).
Érdemes megjegyezni, hogy a diffúzív trajektóriák közötti fázisviszonyok nem csak a mágneses térből adódó Aharonov Bohm fázis segítségével hangolhatók, hanem az elektronok Fermi-hullámhosszának változtatásával is, amit a mintára tett feszültséggel, vagy egy szomszédos kapuelektróda potenciáljának változtatásával érhetünk el.
Gyenge lokalizáció
 |
| 1. ábra. Vezetőképesség fluktuációk |
 |
| 1. ábra. Vezetőképesség fluktuációk |
Hőmérsékleti miatti koherenciavesztés
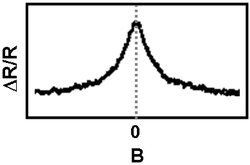
Alacsony hőméréskleten látszik az oszcilláció a mágneses tér függvényében, magasabb hőmérsékleten azonban elmosódik.
Az interferenciakép eltűnésének az okai:
- Környezet miatti dekoherencia
- Hőmérsékleti miatti fázis kiátlagolódás
 |
 |
| 1. ábra. | 1. ábra. |
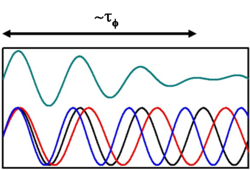
Véges hőmérsékleten a Fermi energia körüli kT tartományban különböző energiájú elektronok propagálnak. Koherens összeadás esetén is a fázisok kiátlagolódnak!
$$\sim \int \limits_{E_F-kT/2}^{E_F+kT/2} e^{i E t / \hbar} \mathrm{d}E$$
A nanoszerkezeten az elektronok átlagosan $\tau_c$ idő alatt haladnak át. Az ehhez tartozó karakterisztikus energia: Thouless energia, $E_T=\hbar/\tau_c$ $\longrightarrow$ $\sim kT > E_T$ hőmérsékleten lesz jelentős ez a kiátlagolódás
Környezet miatti koherenciavesztés
 |
| 1. ábra. |
- Alsó ágon haladó eletronhullám: $|1\rangle$
- Felső ágon haladó eletronhullám: $|2\rangle$
Teljes hullámfügvény: $$|\Psi\rangle = (\alpha|1\rangle + \beta|2\rangle)|\Phi_{env}\rangle\;\;\longrightarrow\;\;\alpha|1\rangle|\Phi_{env1} + \beta|2\rangle|\Phi_{env2}$$
Transzmissziót mérünk: (T operátor csak az elektron hullámfüggvényekre hat, a környezetre nem!) $$\langle\Psi|T|\Psi\rangle = |\alpha|^2 \langle 1|T|1\rangle + |\beta|^2 \langle 2|T|2\rangle + \alpha^*\beta \langle 1|T|2\rangle \langle \Phi_{env1}|T|\Phi_{env2}\rangle + \beta^*\alpha \langle 2|T|1\rangle \langle \Phi_{env2}|T|\Phi_{env1}\rangle$$
Ha $\langle \Phi_{env1}|\Phi_{env2}\rangle \rightarrow 0$, akkor elveszik az interferencia!
- Azaz ha a felül és alul haladó parciális elektronhullám különböző nyomot hagy a környezetben, akkor nem látunk interferenciát. Erre jó példa a fonon szórás, mely a hőmérséklet növelésével egyre jelentősebb dekoherenciához vezet.
Egyszerű példa (Stern, Aharonov, Imry)
 |
| 1. ábra. Vezetőképesség fluktuációk |
Az alsó ágon haladó részecske hullámfügvénye megváltozik a kölcsönhatás miatt: $|u_2(x)|\cdot e^{-i(E+V(q-x))\cdot t/\hbar}$
- A kölcsönhatás ideje alatt felszedett fázis: $\Phi$.
- q bizonytalansága miatt a fázis is bizonytalan: $\Delta \Phi = \frac{1}{\hbar} \frac{\partial V}{\partial q} \cdot \Delta q \cdot t$
- Ha a fázisbizonytalanság nagy lesz, elveszik az interferencia:
$$\Delta \Phi > 1 \Leftrightarrow \frac{\partial V}{\partial q} \cdot t > \frac{\hbar}{\Delta q}$$
Töltött részecske, mely csak az alsó ágon áthaladó elektronnal hat kölcsön (a felső ágon haladó elektronnal elhanyagolható a kölcsönhatás). Helykoordináta: $q$, helybizonytalanság: $\Delta q$
- Ha alul halad az elektron, a töltött részecske gyorsul az erő hatására. Kölcsönhatás ideje (t) alatt az impulzusváltozás: $\delta p = \frac{\partial V}{\partial q}\cdot t$
- Ha az impulzus változás nagyobb az impulzus bizonytalanságnál,akkor a részecske tárolta az "útinformációt":
$$\delta p > \Delta p \Leftrightarrow \frac{\partial V}{\partial q}\cdot t > \frac{\hbar}{\Delta q} \Leftrightarrow \langle\chi_1|\chi_2\rangle<<1$$
Ugyan az a két feltétel! Ugyanakkor veszik el az interferencia, amikor a környezet állapota megkülönbözethetővé válik alul illetve felül haladó elektron esetén!
Környezet miatti koherenciavesztés Aharonov Bohm gyűrűben
Ha a kétrés kísérletben megmondható, hogy az elektron melyik résen haladt át (nyomot hagy a környezetében) $\rightarrow$ interferencia megszűnik.
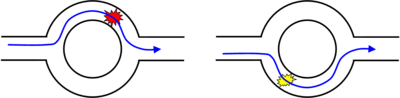
Interferométer: Aharonov - Bohm elrendezés QDot-tal az egyik ágban.
„Útvonal” detektor = QDot + mellette kvantum vezeték (QPC): a Dotban lévő elektron visszaszórást okoz QPC-ben, minél több e-t szór vissza a QPC-ban, annál nagyobb nyomot hagy a környezetén.
Környezet miatti koherenciavesztés: a környezetben minnél nagyobb nyomot hagy az $e \rightarrow |\langle \Phi_{env1}|\Phi_{env2}\rangle|$ csökken $\rightarrow$ az interferencia láthatósága csökken (láthatóság: $\nu = Ampl/Avg$)
- Detektor „érzékenységét” QPC-ra adott ($V_d$) feszültség növelésével javíthatjuk: $I_{QPC}$ nő, több elektront tud visszaszórni.
- A detektor érzékenységének a növelésével az interferencia láthatósága csökken!
</wlatex>
