1. Tér és idő
Történelmünk során a helymeghatározás (navigáció) mindvégig a sikeres kereskedés és a felfedezések egyik fontos kelléke volt. A fejlődést jól példázza, hogy míg Kolumbusz Kristóf egy hosszas és bizonytalan út során India helyett egy új földrészre jutott el, addig napjainkban bárki vásárolhat GPS készüléket, amellyel néhány méteres pontossággal meghatározhatja a helyét bárhol a Földön. A GPS rendszer jól példázza, hogy hogyan lehet széleskörű természettudományos ismeretek felhasználásával egy informatikai csúcsteljesítményt létrehozni, hiszen e hétköznapi eszköz működéséhez az idő ns-os pontosságú mérésétől, relativisztikus korrekciók figyelembevételén keresztül a koordináták bonyolult geometriai meghatározásáig számos fizikai és matematikai ismeretre van szükség. Az idő és távolság fogalma és mérési módszerei, illetve a különböző koordinátarendszerek a természettudományos ismereteik kiindulópontjai, melyek ismerete a mindennapi mérnöki gyakorlatban is elengedhetetlen fontosságú.
Tartalomjegyzék |
Időmérés
Természetes periódusok
Az ember érzékeli az idő múlását, és meg tudja becsülni az eltelt időt. De az idő egészen másképp telik, ha unatkozunk, várunk valakit, vagy ha jól érezzük magunkat.
Az idő objektív mérését az őskor óta különböző természetes periódusok segítették. Ilyen elsősorban a nap (a nappalok és éjszakák változása), a hónap (a Hold fázisainak változása) és az év (az évszakok változása). De ezen kívül is rengeteg periodikus jelenség használható időmérésre: az atomi rezgések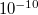 
másodperces periódusidejétől a Föld tengelyének ~ 25-ezer éves periódusáig.
A hétköznapi életben és a tudományban is használt időegység, a másodperc (ami körülbelül két szívverés közt eltelt időtartam) ókori eredetű: a napot kétszer 12 részre osztott része az óra, ennek 60-ad része a perc, és a perc 60-ad része a másodperc. (A 12-részre osztás az év 12 hónapra való osztásának analógiájára történt, a 60-as szám a babilóniai számrendszerből ered.)
De a másodperc pontos meghatározásához tudnunk kell, hogy pontosan milyen hosszú egy nap.
Milyen hosszú egy nap?
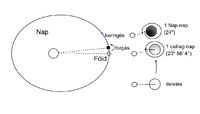
Egy nap hossza a Nap delelésétől a következő delelésig eltelt idő. Ez az idő viszont az év során szabályosan változik, tehát a Nap két delelése között nem mindig ugyanannyi idő telik el!
A Föld – első közelítésben – egyenletesen forog az állócsillagokhoz képest. Ennek periódusa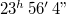 
(csillag-nap). Ugyanakkor a Nap két delelése között ennél hosszabb idő telik el, mert 1 nap alatt a Föld átlagosan majdnem 1°-ot elmozdul a Nap körül, ezért ennyivel többet is kell forognia, hogy a Nap újra deleljen (1. ábra). Ebből adódik átlagosan az a 3' 56", ami a csillagnapot 24 órára (átlagos Nap-nap) kiegészíti. Azért csak átlagosan, mert a Föld ellipszis pályája és tengelyferdesége miatt ez az idő, és így a napok valódi hossza néhány másodperccel ingadozik. Az óráink persze egyenletesen járnak, a néhány másodperces napi eltérések összeadódnak, és így a Nap delelése egy adott helyen az év folyamán kb. ±15 perccel ingadozik. Ezt az ingadozást adja meg az úgynevezett időegyenlet – ami valójában egy függvény.
Az ellipszis pálya hatása: Az ellipszis pályán a Föld napközelben nagyobb szögsebességgel halad, mint naptávolban, ezért napközelben többet kell forognia a Földnek, és így hosszabb a Nap-nap, mint naptávolban.
A tengelyferdeség hatása: Ha a Föld körpályán mozogna a Nap körül, akkor se lennének egyforma hosszúak a napok a tengelyferdeség miatt. A Nap az ekliptikán mozogna csak egyenletesen, ennek vetülete az egyenlítő síkjára viszont már nem egyenletes.
A másodperc-etalon
A másodpercet tehát eredetileg az átlagos Nap-nap segítségével lehetett meghatározni, annak 1/86400-ad része. A Föld forgása azonban a távoli csillagokhoz képest se egyenletes: a Hold és a Nap árapály keltő hatása miatt folyamatosan lassul, különböző okokból pedig kisebb szabálytalan változásokat szenved. (Emiatt az óráink túl gyorsan járnak, a Föld forgását figyelő nemzetközi szervezet (IERS) ezt néhány évente szökőmásodperc beiktatásával korrigálja.)
A méréstechnika fejlődése és a tudományos igények növekedése szükségessé tette a másodperc nagyobb pontosságú és a Föld forgásától független meghatározását. Erre atomi rezgések periódusidejének mérése ad lehetőséget. 1967 óta a másodperc definiálása a cézium atomóra segítségével történik:
A másodperc az alapállapotú cézium-133 atom két hiperfinom energiaszintje közötti átmenetnek megfelelő sugárzás 9192631770 periódusának időtartama.
Távolságmérés
Természetes hosszegységek
Kezdetben a kisebb hosszúságokat az emberi test részeihez hasonlították. Így alakult ki pl. a hüvelyk (inch, Zoll), a láb (foot), a yard (kb. egy lépés hossza). Nagyobb távolságokra a földmérés, hajózás gyakorlatából születtek távolságegységek (pl. mérföld). Ezek pontos értéke más-más volt különböző országokban, városokban, megnehezítve ezzel a hosszúságok egyértelmű megadását.
Érdekes megemlíteni, hogy már régebben is használtak olyan távolságegységeket, amelyek a távolságot idővel fejezik ki: ilyen a „napi járóföld” és később a fényév. Erre később visszatérünk.
A méter eredeti definíciója
A méter, a metrikus mértékegységrendszer névadója, ennek az összevisszaságnak a megszüntetésére született. A másodperchez hasonlóan a métert is először a Föld adataihoz kötötték: 1 méter a Föld kerületének (a Párizson átmenő délkörnek) 1/40000000-od része. Az ez alapján platina-irídium ötvözetből elkészített méter etalont Párizsban őrzik.
A Föld kerületének mérése azonban nem a modern időkben kezdődött: Eratosthenes már az időszámítás előtti III. században meglepősen pontos méréseket végzett Egyiptomban.
A kinematika alapjai
A tömegpont helyének megadása az idő függvényében
A kinematika a mozgás leírásával foglalkozik, a mozgás okainak vizsgálata nélkül. Egy valóságos test, például egy ember vagy a Föld légköre mozgásának leírása azonban így is nagyon bonyolult. A fogalmak, módszerek, összefüggések megismeréséhez egyszerűbb modelleket kell választanunk.
A legegyszerűbb modell a pontszerű test, vagy tömegpont. Ebben a modellben nem foglalkozunk a test alakjával, esetleges alakváltozásával, forgásával, hanem csak a pontszerűnek tekintett test haladó mozgásával. Ez a modell jól alkalmazható olyan mozgásokra, ahol a test mérete sokkal kisebb, mint az elmozdulások. Ez nem jelenti azt, hogy a test „kicsi”: például a Föld pontszerű testként kezelhető, ha a Nap körüli mozgását írjuk le.
Egy tömegpont mozgását egyértelműen leírjuk, ha megadjuk a helyét – egy kiválasztott kezdőpontból (origó) a tömegponthoz mutató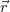 
vektort – az idő (
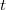) függvényében: 
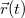. A függvény általános esetben nagyon bonyolult lehet.
A mozgás során a test által befutott pontok összessége a pálya. Ez az a görbe, ami a test halad. Ha a pálya egy síkban van, akkor síkmozgásról beszélünk. Ezek közül a gyakorlatban kiemelkedően fontos a körmozgás, a bolygómozgás (ellipszis pálya) és a hajítások (parabola pálya). A legegyszerűbb pálya az egyenes: ilyen mozgás az egyenes vonalú egyenletes mozgás és az egyenes vonalú gyorsuló mozgás, de egyenes vonalú mozgások lehetnek a rezgések is.
Az elmozdulás vektoriális mennyiség, a helyvektor megváltozása: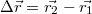 
.
Ezzel szemben az út (
) skaláris mennyiség, a test által a vizsgált idő alatt befutott pályadarab hossza. Nagyon kis elmozdulásoknál 
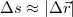, infinitezimálisan 
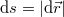, így a teljes utat az elemi utak összegzésével lehet meghatározni: 
.
A vektorokkal való számításokra vissza fogunk térni a koordinátarendszereknél.
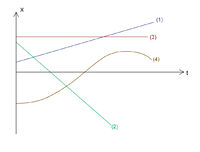
Egyenes vonalú (egydimenziós) mozgásoknál az elmozdulás is skalár függvény: 
. Ezt az elmozdulás-idő grafikonon szemléltethetjük (2. ábra).
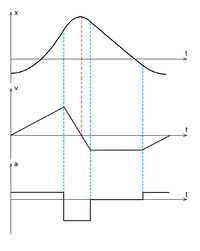
A grafikonokról nem csak az egyes testek helye olvasható le az idő függvényében, hanem a mozgások egyéb jellemzői is. Ha a függvény nő, akkor a test a koordinátarendszerben pozitív irányban, „előre” mozog (1), ha csökken, akkor negatív irányban, „hátra” (2), ha pedig a függvény konstans, akkor a test áll (3).
A görbe meredeksége azt mutatja, hogy egységnyi idő alatt mekkora a test elmozdulása. Tehát a meredekebb görbe a gyorsabb test mozgását ábrázolja. Ha a függvény lineáris (a görbe egyenes), akkor a test egyenletesen mozog, ellenkező esetben a mozgás nem egyenletes, a test gyorsul vagy lassul (4).
A függvények vizsgálatával a matematikai analízis foglalkozik, amelyet a XVII. században Newton és Leibnitz többek közt éppen mechanikai problémák megoldására fejlesztett ki. Ennek segítségével a hétköznapi életben is használt sebesség és gyorsulás fogalmaknak pontosabb meghatározását adhatjuk.
Sebesség és gyorsulás
A sebesség a hétköznapi életben is jól ismert fogalom. Aki közlekedik, biciklizik, autót vezet, többé-kevésbé meg tudja becsülni pillanatnyi sebességét, de ebben segíti a sebességmérő is.
Hosszabb úton fontos információ az átlagsebesség is. Ezt az összes megtett út és a mozgáshoz szükséges teljes idő hányadosaként kapjuk:![\[v_{{\rm atl}} =\frac{s_{{\rm ossz}}}{t_{{\rm ossz}}}\]](/images/math/6/7/4/67440eba146c0ba0de95113242707b26.png)
![\[v\approx\frac{\Delta s}{\Delta t}\]](/images/math/e/8/9/e897d9006b2acbbb4cc629e416037fab.png)
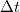tart 0-hoz, megkapjuk a pillanatnyi sebességet: ![\[v=\lim_{\Delta t\to 0}\frac{\Delta s}{\Delta t}=\frac{{\rm d}s}{{\rm d}t}\]](/images/math/3/a/e/3ae1e07b5cf88f4e9cb19bfc5e65ff03.png)
![\[\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}\]](/images/math/8/a/3/8a3cff45b4e1c72011b383d6f1f3b7fb.png)
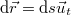, ahol 
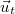az érintő irányú (tangenciális) egységvektor, a sebességvektor ![\[\vec{v}=\frac{{\rm d}s}{{\rm d}t}\vec{u}_t=v\vec{u}_t\]](/images/math/9/1/f/91f7ef84da4cc2b8639706438e5f166d.png)
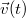sebesség-idő függvény ismeretében meghatározható a test helye az idő függvényében: ![\[\vec{r}(t)=\int_0^t\vec{v}(\tau){\rm d}\tau+\vec{r}(0)\]](/images/math/7/2/f/72f0bce2474849f5e4fe2149b7b3324d.png)
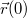a test helyvektora a 
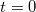időpillanatban.
A test által megtett út pedig az ![\[s(t)=\int_0^t v(\tau){\rm d}\tau\]](/images/math/e/b/9/eb91985eb33d875ad2bd4005977d0c88.png)
![\[\vec{a}=\frac{{\rm d}\vec{v}}{{\rm d}t}=\frac{{\rm d^2}\vec{r}}{{\rm d}t^2}\]](/images/math/b/6/e/b6e6e84dcab5e5ad7ea9bdc30fc3bb6a.png)
![\[\vec{a}=\frac{{\rm d}v}{{\rm d}t}\vec{u}_t+v\frac{{\rm d}\vec{u}_t}{{\rm d}t}\]](/images/math/b/c/7/bc7d790f06da2833dec88e38ae72e4e7.png)
![\[a_t=\frac{{\rm d}v}{{\rm d}t}\]](/images/math/1/3/7/1375845315ebf89272d11f8c66204205.png)
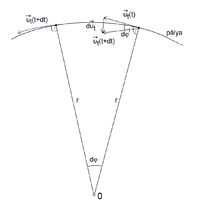
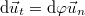, ahol 
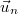a pályára merőleges (normális), befelé mutató egységvektor, 
pedig a pálya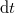 
idő alatti elfordulása, ami szintén az ábráról leolvashatóan ![\[{\rm d}\varphi=\frac{v{\rm d}t}{r}\]](/images/math/c/3/7/c37ecc0b9e8b4b4b716257989f689d67.png)
![\[a_n=\frac{v^2}{r}\]](/images/math/4/5/4/454d849fbbdd7843e0af6c8ebf34ed9d.png)
A gyorsulásvektor tehát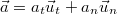 
alakban írható, ahol 
a gyorsulás érintőirányú (tangenciális),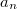 
az erre merőleges (normális) komponensének nagysága, 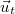és 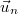pedig a megfelelő egységvektorok.
gyorsulás-idő függvény ismeretében meghatározható a test sebessége, abból pedig a helye az idő függvényében: ![\[\vec{v}(t)=\int_0^t\vec{a}(\tau){\rm d}\tau+\vec{v}(0)\]](/images/math/e/a/6/ea6b77cbb71a948cc710266d327eb418.png)
![\[\vec{r}(t)=\int_0^t\vec{v}(\tau){\rm d}\tau+\vec{r}(0)=\int\!\!\!\int_0^t\vec{a}(\tau){\rm d}\tau+\int_0^t\vec{v}(0){\rm d}\tau+\vec{r}(0)=\int\!\!\!\int_0^t\vec{a}(\tau){\rm d}\tau+\vec{v}(0)t+\vec{r}(0)\]](/images/math/3/f/3/3f3de2637c735b0e178a5fa2d63e8ffc.png)
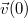a test sebessége, 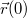pedig a helyvektora a 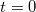időpillanatban.
![\[v(t)=\frac{{\rm d}x}{{\rm d}t}\]](/images/math/c/6/5/c65c4494b240b7448dc14c2329764fa0.png)
![\[a(t)=\frac{{\rm d}v}{{\rm d}t}=\frac{{\rm d^2}x}{{\rm d}t^2}\]](/images/math/7/d/f/7dfff538cd24a6ba6cbea9b491a93926.png)
![\[v(t)=\int_0^t a(\tau){\rm d}\tau+v(0)\]](/images/math/1/f/9/1f91cf91d9cbfcbdbc995b76157ba9b0.png)
![\[x(t)=\int_0^t v(\tau){\rm d}\tau+x(0)=\int\!\!\!\int_0^t a(\tau){\rm d}\tau+\int_0^t v(0){\rm d}\tau+x(0)=\int\!\!\!\int_0^t a(\tau){\rm d}\tau+v(0)t+x(0)\]](/images/math/8/f/e/8fe2c9509a6d720336d67a8d670be9b0.png)
A sebesség SI mértékegysége a m/s, de a hétköznapi életben gyakran használjuk a km/h-t is. 1 km/h = 1000 m / 3600 s = 1/3,6 m/s.
A gyorsulás SI mértékegysége a m/s
. Más mértékegység nem használatos.
Koordinátarendszerek
Descartes-, henger-, gömbi- és általános koordináták
Koordinátarendszerek segítségével a tér (vagy a sík) pontjait, illetve az oda mutató vektorokat rendezett számhármasokkal (számpárokkal) lehet megadni. Így vektorok helyett skalár mennyiségekkel dolgozhatunk.
A legalapvetőbb, és legismertebb koordinátarendszer a Descartes-féle koordinátarendszer. A három (síkban kettő), egymásra kölcsönösen merőleges koordinátatengely (
, 
és 
) az origóban (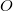
), a koordinátarendszer kiindulópontjában metszi egymást. Egy 
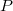pont , illetve koordinátáját a pont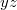 
, 
, illetve 
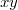síktól való előjeles távolsága határozza meg (5. ábra). A 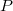pontot így egyértelműen meghatározza az 
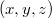rendezett számhármas.
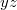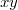A koordinátavonalak (azon pontok halmaza, melyeknek koordinátáit egy kivételével rögzítjük) a tengelyekkel párhuzamos egyenesek, a koordinátafelületek (azon pontok halmaza, melyeknek csak egy koordinátáját rögzítettük) az , , illetve síkokkal párhuzamos síkok.
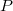pontba mutató 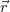helyvektor a koordinátarendszer , , illetve tengelyével párhuzamo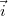s 
, 
és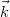 
egységvektorok (más néven bázisvektorok) lineáris kombinációjaként adható meg: ![\[\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}\]](/images/math/c/3/0/c305df5179988591bf69c10dc43bd9da.png)
A mozgások leírásánál az 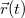vektorfüggvény helyett így három skalárfüggvény: , 
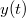és 
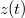használható. Ehhez hasonlóan a 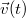vektorfüggvény helyett a 
, 
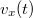és 
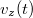skalárfüggvényekkel, az vektorfüggvény helyett az 
, 
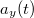és 
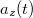skalárfüggvényekkel írható le a test sebessége és gyorsulása.
Descartes-koordináták esetén a vektorok összeadása, kivonása, deriválása, integrálása komponensenként elvégezhető, más koordinátarendszerek esetében azonban ez bonyolultabb. Erre később visszatérünk.
Bár sok szempontból a Descartes-koordináták legegyszerűbbek, bizonyos esetekben célszerű más koordinátarendszerek használata. Hengerszimmetrikus problémák leírására célszerű hengerkoordinátákat (síkban polárkoordinátákat), gömbszimmetrikus esetben pedig gömbi koordinátákat használni. Ezeken a nevezetes koordinátarendszereken kívül azonban további koordinátarendszerek is megadhatók, így röviden kitérünk ilyen, általános koordinátarendszerek tárgyalására is.
A síkban sok feladat (például a bolygómozgás vizsgálata) könnyebben megoldható polárkoordináták segítségével (6. ábra). A 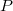pont helyét az origótól mért 
távolság, és egy megadott, origóból kiinduló félegyenestől mért 
vagy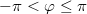 
szöggel lehet megadni. A koordinátavonalak egyrészt az origóból kiinduló félegyenesek (
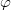állandó), másrészt origó középpontú koncentrikus körök (
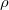állandó). Az 
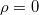pontban 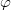értéke tetszőleges lehet.
Hengerszimmetrikus térbeli feladatoknál (például egyenes vezetők körül kialakuló terek számításánál) jól használhatók a hengerkoordináták. Egy 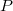pontot a 
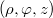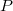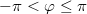koordinátahármas ad meg, ahol a pont tengelytől mért távolsága, a vagy szög a tengelyre illeszkedő kiinduló félsík és a 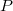ponton átmenő félsík által bezárt szög, pedig a 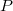pont tengelyre merőleges, origón átmenő síktól mért előjeles távolsága.
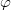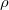Ebben a koordinátarendszerben a koordinátavonalak a tengelyből induló, arra merőleges félegyenesek ( és állandó), a tengellyel párhuzamos egyenesek ( és 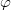állandó), valamint a tengelyre merőleges, koncentrikus körök ( 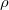és állandó). A koordinátafelületek a tengely körüli hengerfelületek (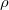 állandó), a tengelyre illeszkedő félsíkok ( 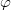állandó) és a tengelyre merőleges síkok ( állandó). A 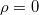koordinátájú pontokban 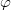itt is tetszőleges értéket vehet fel.
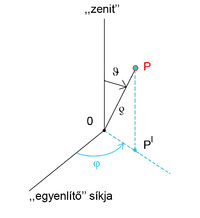
Gömbi koordinátákat gömbszimmetrikus tereknél (például ponttöltés, tömegpont körül) érdemes használni, de lényegében gömbi koordináták a földrajzi koordináták is (csak a radiális távolságot nem a Föld középpontjától, hanem a tengerszinttől mérik).
A 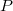pontot megadó 
koordinátahármasban a pont távolsága az origótól, a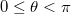 
vagy 
szög (inklináció, földrajzi koordinátáknál a szélesség) a középpontból a ponthoz húzott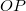 
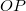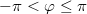egyenes és a koordinátarendszer egyik kiválasztott iránya, a zenit közti szög (vagy az és a zenitre merőleges sík – a földrajzban az egyenlítő síkja – közti szög), a vagy szög (azimut, földrajzi koordinátáknál a hosszúság) pedig az 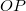egyenes zenitre merőleges síkra való vetületének és a koordinátarendszer másik kiválasztott (a zenitre merőleges) irányának a szöge.
A gömbi koordinátarendszerben a koordinátavonalak a középpontból kiinduló félegyenesek (
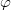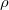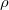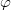és állandó), a zenitre merőleges körök ( és állandó, szélességi körök), valamint a középpont körüli, a zenittel egy síkban fekvő félkörök ( és állandó, hosszúsági körök). A koordinátafelületek gömbök ( 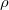állandó), kúppalástok ( állandó) és félsíkok (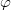 állandó). Az 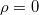koordinátájú pontokban és 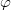is tetszőleges értéket vehet fel. A 
és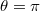 
(vagy a 
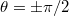) koordinátájú pontoknál (a Földön a sarkokon) 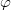szintén tetszőleges értéket vehet fel.
Az általános, görbevonalú koordinátarendszerhez legegyszerűbben úgy juthatunk el, ha egy Descartes koordinátarendszert (két dimenzióban) rugalmas felületre rajzolunk, majd a felületet deformáljuk. Az eredetileg egymással párhuzamos, illetve merőleges koordinátavonalak görbékké torzulnak. Három dimenzióban ehhez hasonlóan a koordinátafelületek is görbültek lesznek. A görbült koordinátarendszerekben a bázis lokális, a hely függvényében változik. A henger és gömbi koordinátarendszerek speciális görbevonalú koordinátarendszerek.
Távolságok, sebességek meghatározása különböző koordinátarendszerekben
Két pont közötti távolságot a legegyszerűbb a Descartes-féle koordinátarendszerben meghatározni, a távolság a (térbeli) Pitagorasz-tétellel a pontok (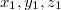
) és (
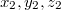)koordinátáiból közvetlenül adódik: ![\[s=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\]](/images/math/2/c/a/2ca1d021354234e4e0fb6adf53196822.png)
Más koordinátarendszerekben két tetszőleges pont távolságának meghatározása bonyolultabb, sokszor legegyszerűbb átszámolni a koordinátákat Descartes-koordinátákba, és a távolságot abból meghatározni.
Polárkoordinátáknál az (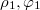
) és a (
) pontok távolsága a cosinus-tétel segítségével adódik: ![\[s=\sqrt{\rho_1^2+\rho_2^2-2\rho_1\rho_2\cos(\varphi_2-\varphi_1)}\]](/images/math/2/4/5/2459ac6b9faab31cf6872a67bb2aa577.png)
![\[s=\sqrt{\rho_1^2+\rho_2^2-2\rho_1\rho_2\cos(\varphi_2-\varphi_1)+(z_2-z_1)^2}\]](/images/math/4/3/9/4392aabdaf020976752abe202d925490.png)
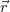pont távolsága az origótól, azaz a pontba mutató helyvektor hossza Descartes-koordinátákkal ![\[r=|\vec{r}|=\sqrt{x^2+y^2+z^2}\]](/images/math/d/3/e/d3e04893c3057bdd0e8f8df2a75f3921.png)
![\[r=|\vec{r}|=\sqrt{\rho^2+z^2}\]](/images/math/9/4/6/9463378711a72af4f581d01427bbf60c.png)
![\[r=|\vec{r}|=\rho\]](/images/math/7/8/8/788e9178a7106b91250c417f061c814d.png)
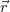helyvektor és a 
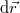elemi elmozdulásvektor az 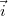, , 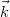egységvektorok segítségével azonnal adódik: ![\[\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}\qquad {\rm d}\vec{r}={\rm d}x\vec{i}+{\rm d}y\vec{j}+{\rm d}z\vec{k}\]](/images/math/7/9/8/7986e3c1fb324023e9360d3246e36880.png)
Görbe vonalú koordinátarendszereknél azonban a bázis lokális, azaz az egységvektorok a hely függvényében változnak, így érdemes megadnunk a bázisvektorok elemi megváltozásait is.
Polárkoordinátáknál (síkban) a bázis az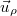
sugár irányú és az 
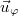érintő irányú (a kör alakú koordinátavonalat érintő) lokális egységvektorokból áll. Az 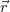helyvektor és a 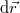elemi elmozdulásvektor (azaz a 
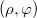pontból a 
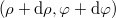pontba mutató vektor) a bázis segítségével: ![\[\vec{r}=\rho\vec{u}_\rho\qquad {\rm d}\vec{r}={\rm d}\rho\vec{u}_\rho+\rho{\rm d}\varphi\vec{u}_\varphi\]](/images/math/4/0/9/409b43a45e81ca2d6fb2bc61a40f8ce0.png)
![\[{\rm d}\vec{u}_\rho={\rm d}\varphi\vec{u}_\varphi\qquad {\rm d}\vec{u}_\varphi=-{\rm d}\varphi\vec{u}_\rho\]](/images/math/7/7/8/77849a7ed1625426454794f482c4eb9a.png)
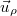sugár irányú, az 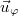érintő irányú (a kör alakú koordinátavonalat érintő) és az 
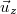tengellyel párhuzamos irányú egységvektorokból áll (ahol az első kettő pontról pontra változik, az utolsó viszont mindenhol ugyanaz). Az 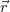helyvektor és a 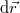elemi elmozdulásvektor (azaz a 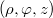pontból a 
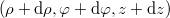pontba mutató vektor) a bázis segítségével: ![\[\vec{r}=\rho\vec{u}_\rho+z\vec{u}_z\qquad {\rm d}\vec{r}={\rm d}\rho\vec{u}_\rho+\rho{\rm d}\varphi\vec{u}_\varphi+{\rm d}z\vec{u}_z\]](/images/math/2/f/6/2f6789ad5a14392ae5dfdc97a53bb42c.png)
![\[{\rm d}\vec{u}_\rho={\rm d}\varphi\vec{u}_\varphi\qquad {\rm d}\vec{u}_\varphi=-{\rm d}\varphi\vec{u}_\rho \qquad {\rm d}\vec{u}_z=0\]](/images/math/8/6/a/86aa07df32ea85c6f647675572218694.png)
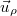sugár irányú, az 
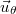és az 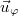érintő irányú (a zenittel egy síkban lévő félkörök, illetve a zenitre merőleges körök érintői) egységvektorokból áll. Most mind a három egységvektor pontról pontra változik. Az 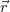helyvektor és a 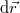elemi elmozdulásvektor (azaz a 
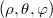pontból a 
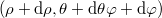pontba mutató vektor) a lokális bázissal kifejezve: ![\[\vec{r}=\rho\vec{u}_\rho\qquad {\rm d}\vec{r}={\rm d}\rho\vec{u}_\rho+\rho{\rm d}\theta\vec{u}_\theta+\rho\sin\theta{\rm d}\varphi\vec{u}_\varphi\]](/images/math/0/b/4/0b40438d13047da42318d9bb55865af5.png)
![\[{\rm d}\vec{u}_\rho={\rm d}\theta\vec{u}_\theta+\sin\theta{\rm d}\varphi\vec{u}_\varphi \qquad {\rm d}\vec{u}_\theta=-{\rm d}\theta\vec{u}_\rho+\cos\theta{\rm d}\varphi\vec{u}_\varphi \qquad {\rm d}\vec{u}_\varphi=-\sin\theta{\rm d}\varphi\vec{u}_\rho-\cos\theta{\rm d}\varphi\vec{u}_\theta\]](/images/math/9/4/5/9450529abe7304db68fed2b81eb515f2.png)
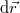elemi elmozdulásvektorból -vel való osztással, vagy az helyvektorból deriválással (ekkor azonban figyelnünk kell arra, hogy az egységvektorok nem állandók!) a különböző koordinátarendszerekben már meghatározhatók. A Descartes-féle koordinátarendszerben a komponensek egymástól függetlenek, a sebesség: ![\[\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}=\frac{{\rm d}x}{{\rm d}t}\vec{i}+\frac{{\rm d}y}{{\rm d}t}\vec{j}+\frac{{\rm d}z}{{\rm d}t}\vec{k}=v_x\vec{i}+v_y\vec{j}+v_z\vec{k}\]](/images/math/9/d/0/9d00f378dfc6c47b4658b9b596c6792d.png)
![\[\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}=\frac{{\rm d}\rho}{{\rm d}t}\vec{u}_\rho+\rho\frac{{\rm d}\varphi}{{\rm d}t}\vec{u}_\varphi\]](/images/math/f/3/5/f359dfe2263e609a4d91a76990cb9dd9.png)
![\[\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}=\frac{{\rm d}\rho}{{\rm d}t}\vec{u}_\rho+\rho\frac{{\rm d}\varphi}{{\rm d}t}\vec{u}_\varphi+\frac{{\rm d}z}{{\rm d}t}\vec{u}_z\]](/images/math/0/8/e/08ed3166cfb4980e3ec3a8f9fa1345be.png)
![\[\vec{v}=\frac{{\rm d}\vec{r}}{{\rm d}t}=\frac{{\rm d}\rho}{{\rm d}t}\vec{u}_\rho+\rho\frac{{\rm d}\theta}{{\rm d}t}\vec{u}_\theta+\rho\sin\theta\frac{{\rm d}\varphi}{{\rm d}t}\vec{u}_\varphi\]](/images/math/f/6/1/f61948c41ef480f4857e50f8b2f002d3.png)
![\[\vec{a}=\frac{{\rm d}\vec{v}}{{\rm d}t}=\frac{{\rm d^2}\vec{r}}{{\rm d}t^2}=\frac{{\rm d^2}x}{{\rm d}t^2}\vec{i}+\frac{{\rm d^2}y}{{\rm d}t^2}\vec{j}+\frac{{\rm d^2}z}{{\rm d}t^2}\vec{k}=a_x\vec{i}+a_y\vec{j}+a_z\vec{k}\]](/images/math/1/1/7/1173b64cae4156f6f00edb85d9a4a611.png)
![\[\vec{a}=\frac{{\rm d}\vec{v}}{{\rm d}t}=\frac{{\rm d^2}\vec{r}}{{\rm d}t^2}=\left[\frac{{\rm d^2}\rho}{{\rm d}t^2}-\rho\left(\frac{{\rm d}\varphi}{{\rm d}t}\right)^2\right]\vec{u}_\rho+\left(\rho\frac{{\rm d^2}\varphi}{{\rm d}t^2}+2\frac{{\rm d}\rho}{{\rm d}t}\frac{{\rm d}\varphi}{{\rm d}t}\right)\vec{u}_\varphi\]](/images/math/f/2/4/f24993ab3839277274d6aedb88df1780.png)
Látható, hogy 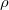állandó értéke mellett is lehet sugárirányú gyorsulás (pl. körmozgásnál a centripetális gyorsulás).
![\[\vec{a}=\frac{{\rm d}\vec{v}}{{\rm d}t}=\frac{{\rm d^2}\vec{r}}{{\rm d}t^2}=\left[\frac{{\rm d^2}\rho}{{\rm d}t^2}-\rho\left(\frac{{\rm d}\varphi}{{\rm d}t}\right)^2\right]\vec{u}_\rho+\left(\rho\frac{{\rm d^2}\varphi}{{\rm d}t^2}+2\frac{{\rm d}\rho}{{\rm d}t}\frac{{\rm d}\varphi}{{\rm d}t}\right)\vec{u}_\varphi+\frac{{\rm d^2}z}{{\rm d}t^2}\vec{u}_z\]](/images/math/d/f/d/dfd275f0511dd9f80eb35e98a329543a.png)
![\[\vec{a}=\frac{{\rm d}\vec{v}}{{\rm d}t}=\frac{{\rm d^2}\vec{r}}{{\rm d}t^2}=\left[\frac{{\rm d^2}\rho}{{\rm d}t^2}-\rho\left(\frac{{\rm d}\theta}{{\rm d}t}\right)^2-\rho\sin^2\theta\left(\frac{{\rm d}\varphi}{{\rm d}t}\right)^2\right]\vec{u}_\rho+\]](/images/math/f/1/e/f1e7cb6c6e635b88d63966ecbe703dee.png)
![\[+\left[\rho\frac{{\rm d^2}\theta}{{\rm d}t^2}+2\frac{{\rm d}\rho}{{\rm d}t}\frac{{\rm d}\theta}{{\rm d}t}-\rho\sin\theta\cos\theta\left(\frac{{\rm d}\varphi}{{\rm d}t}\right)^2\right]\vec{u}_\theta+\]](/images/math/f/d/9/fd93fcd404525a1a338a9ee6df1cb5ae.png)
![\[+\left(\rho\sin\theta\frac{{\rm d^2}\varphi}{{\rm d}t^2}+2\sin\theta\frac{{\rm d}\rho}{{\rm d}t}\frac{{\rm d}\varphi}{{\rm d}t}+2\rho\cos\theta\frac{{\rm d}\theta}{{\rm d}t}\frac{{\rm d}\varphi}{{\rm d}t}\right)\vec{u}_\varphi\]](/images/math/4/9/e/49e75febff7ecbe556d10001af57b292.png)
Koordináta-transzformációk
Ha egy pont koordinátáit ismerjük egy koordinátarendszerben, akkor transzformációs összefüggések segítségével kiszámíthatók egy másik koordinátarendszerben is a koordináták.
Koordináta-transzformációkkal áttérhetünk egy ugyanolyan típusú, de az eredetitől különböző kezdőpontú vagy irányítottságú másik koordinátarendszerre, például egy Descartes-koordinátarendszerből egy másik Descartes-koordinátarendszerbe. Ha az eredeti K koordinátarendszerben a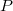 pont koordinátái 
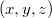, akkor a K-hoz képest a 
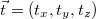vektorral eltolt K' koordinátarendszerben a pont koordinátái ![\[x'=x-t_x\]](/images/math/f/5/c/f5c5cabc3219766d25024b19b5848d64.png)
![\[y'=y-t_y\]](/images/math/f/0/2/f02ff92575d5c82099f5f227bf7b1ace.png)
![\[z'=z-t_z\]](/images/math/6/a/5/6a5894e727ae4e27164b562469ec61fb.png)
szöggel van elforgatva, akkor egy 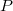pont K'-beli 
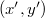koordinátáit a K-beli 
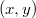koordinátákból a következő transzformációs összefüggésekkel számíthatjuk: ![\[x'=x\cos\theta+y\sin\theta\]](/images/math/f/7/a/f7a3eddcaacfd06f738aeb84c476f896.png)
![\[y'=-x\sin\theta+y\cos\theta\]](/images/math/3/5/2/352360c9e3dff9526c1a634137d65aae.png)
Általános háromdimenziós elforgatás számítása bonyolultabb. Az elforgatás megadására több lehetőség van: meg lehet adni a forgatás szögét és a forgástengely irányába mutató egységvektort, vagy a kettő szorzataként előálló forgásvektort, vagy az Euler által bevezetett Euler-szögeket. Az új koordináták ebben az esetben is az eredeti koordináták lineáris kombinációjaként írhatók fel.
Különböző típusú koordinátarendszerek közötti transzformációk közül néhány fontosabb:
Hengerkoordinátákból Descartes-koordinátákba (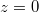
esetén polárkoordinátákból kétdimenziós Descartes-koordinátákba), azonos origó, közös -tengely esetében ![\[x=\rho\cos\varphi\]](/images/math/7/c/9/7c99b38af55c3bdea887499aa4900f6b.png)
![\[y=\rho\sin\varphi\]](/images/math/1/8/e/18eb254be814155aacd5dfc4e366223d.png)
![\[z=z\]](/images/math/8/9/9/899d4ef490389c29b8d9134a5ee6032d.png)
a zenittel egy irányba mutat) ![\[x=\rho\sin\theta\cos\varphi\]](/images/math/d/8/7/d87b0406fd346e6982cd8e1d58d78c6b.png)
![\[y=\rho\sin\theta\sin\varphi\]](/images/math/9/3/c/93cf272ffc76a28abd02399f908dfb2d.png)
![\[z=\rho\cos\theta\]](/images/math/3/3/e/33e2a769ab7e3ab176c416067522e203.png)
![\[\rho=\sqrt{x^2+y^2}\]](/images/math/3/d/c/3dcec16fe709286abad1f0a11ec76ad6.png)
![\[\varphi=\arctan{\frac{y}{x}}\qquad{\rm (ha}\quad x>0, y\geq0{\rm )}\]](/images/math/0/c/8/0c855d458137535832e68458e8a3bca6.png)
![\[\rho=\sqrt{x^2+y^2+z^2}\]](/images/math/6/b/9/6b93a1b7251205b098edd31be91f0d7f.png)
![\[\theta=\arctan{\frac{\sqrt{x^2+y^2}}{z}}\qquad{\rm (ha}\quad z>0{\rm )}\]](/images/math/b/2/b/b2b82c4bdbb658016e541809478f14e7.png)
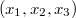, akkor a K'-beli 
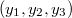koordinátákat ![\[y_1=y_1(x_1, x_2, x_3)\]](/images/math/a/7/9/a796aefff649c48291f4cfe64f84e7db.png)
![\[y_2=y_2(x_1, x_2, x_3)\]](/images/math/c/6/c/c6c4979c1122c5a6d280a324b248fcf9.png)
![\[y_3=y_3(x_1, x_2, x_3)\]](/images/math/5/f/1/5f1cf2423e8369ba9a8c6444834d3606.png)
![\[\mathbf{J}(x_1,x_2,x_3)=\frac{\partial(y_1,y_2,y_3)}{\partial(x_1,x_2,x_3)}= \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \frac{\partial y_1}{\partial x_3} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \frac{\partial y_2}{\partial x_3} \\ \frac{\partial y_3}{\partial x_1} & \frac{\partial y_3}{\partial x_2} & \frac{\partial y_3}{\partial x_3} \end{bmatrix}\]](/images/math/f/0/7/f077703a0ebdb06e93c57bd3535af780.png)
A mátrix determinánsa (a Jacobi-determináns) fontos információkat ad a transzformációról. Ha a determináns egy adott pontban nem nulla, akkor a pont környezetében a mátrix invertálható, és így a transzformáció kölcsönösen egyértelmű. Ezen kívül a Jacobi-determináns nagysága megadja, hogy a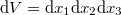 
elemi térfogat hányszorosára nő (vagy hányad részére csökken) a transzformáció hatására, pozitív vagy negatív előjele pedig azt mutatja meg, hogy a transzformáció megtartja vagy megfordítja-e a bázis irányítottságát.
Példaképpen a gömbi koordinátákat Descartes-koordinátákba átvivő transzformáció Jacobi-mátrixa:
![\[\mathbf{J}(\rho,\theta,\varphi)=\frac{\partial(x,y,z)}{\partial(\rho,\theta,\varphi)}= \begin{bmatrix} \frac{\partial x}{\partial\rho} & \frac{\partial x}{\partial\theta} & \frac{\partial x}{\partial\varphi} \\ \frac{\partial y}{\partial\rho} & \frac{\partial y}{\partial\theta} & \frac{\partial y}{\partial\varphi} \\ \frac{\partial z}{\partial\rho} & \frac{\partial z}{\partial\theta} & \frac{\partial z}{\partial\varphi} \end{bmatrix}= \begin{bmatrix} \sin\theta\cos\varphi & \rho\cos\theta\cos\varphi & -\rho\sin\theta\sin\varphi \\ \sin\theta\sin\varphi & \rho\cos\theta\sin\varphi & \rho\sin\theta\cos\varphi \\ \cos\theta & -\rho\sin\theta & 0 \end{bmatrix}\]](/images/math/b/d/4/bd4e5c9bd8cf647e974829811928fcb9.png)
![\[{\rm det}({\bf J})=\rho^2\sin\theta\geq 0,\qquad{\rm ha}\quad \rho\neq0,\quad\theta\neq0,\quad\theta\neq\pi\]](/images/math/3/2/1/32167404028d319f434759bfa2c2d8e4.png)
Eszerint a transzformáció ezeken a pontokon kívül kölcsönösen egyértelmű, megfordítható. A transzformáció a bázis irányítottságát sehol nem változtatja meg, viszont az elemi térfogatot általában csökkenti vagy növeli.
Távolságmérés idővel
A fénysebesség kitüntetett szerepe
A speciális relativitáselmélet szerint egyetlen test se mozoghat gyorsabban, mint a vákuumbeli fénysebesség. A fény (vákuumban) viszont bármely – egymáshoz képest akár nagy sebességgel mozgó – koordinátarendszerből megfigyelve ezzel a sebességgel halad. A fénysebességnek így kitüntetett szerepe van, egyike az alapvető természeti állandóknak.
A fénysebesség mérése nem könnyű. A fénysebesség a hétköznapi életben megszokott sebességekhez képest olyan nagy, hogy sokáig azt hitték, hogy a fény terjedéséhez egyáltalán nem kell idő. Az első nagyságrendileg helyes eredményt adó méréseket Rømer végezte a XVII. században a Jupiter holdjainak megfigyelésével. A későbbiekben különböző technikákkal a fénysebességet egyre pontosabban sikerült meghatározni.
A fénysebesség ismeretében lehetőség van arra, hogy távolságok mérését időmérésre vezessük vissza. Az idő az egyik legpontosabban mérhető mennyiség, így ezzel a módszerrel a távolságokat is nagy pontossággal lehet mérni. Ezt az elvet használja a GPS is: a távolságokat a fénysebességgel haladó rádióhullámok futási idejéből számolja.
SI méter-etalon a fénysebesség értékének rögzítésével
Bay_Zoltán vetette fel, hogy a fénysebesség egyre pontosabb meghatározása helyett legyen a fénysebesség értéke rögzített érték, és a métert éppen ennek segítségével definiáljuk.
1983 óta a fénysebesség értéke definíciószerűen c=299792458 m/s (az akkor elfogadott mért fénysebesség egész m/s-okra kerekített érétke). A méter definíciója azóta: 1 méter a fény által a vákuumban a másodperc 1/299792458-ad része alatt megtett út hossza.
Helymeghatározás csillagászati módszerekkel
A nyílt-tengeri hajózás és az időmérés
A Nap, a Hold és a csillagok, bolygók látszólagos helyzetéből sokféle következtetés levonható. Ha ismerjük a helyet, ahol vagyunk, akkor az égitestek pozíciójából következtethetünk az időre. Így működik a napóra, az egyik legősibb időmérő eszköz. A napóra leolvasása azonban nem olyan egyszerű, mint ahogy elsőre gondolni lehet. Először is a Nap csak az időzóna közepén delel (átlagosan) délben, a többi helyen ehhez képest hosszúsági fokonként 4 perccel eltolódva (hiszen a Föld átlagosan 24 óra alatt fordul 360°-ot). Azonban az időzóna közepén is csak átlagosan delel délben, hiszen ahogy korábban láttuk a delelés időpontja az időegyenlet szerint kb. ±15 perccel ingadozik. A nyári időszámítás során ehhez adódik hozzá még egy további óra eltolódás.
A nyílt tengeri hajózással (amikor a hajósok már hosszabb ideig olyan messzire távolodtak a partoktól, hogy azokat nem láthatták) szükségessé vált a pillanatnyi helyzet csillagászati módszerekkel való meghatározása.
A szélesség (észak-déli irányban mért helyzet) meghatározása éjszaka aránylag egyszerű: a Sarkcsillag (a déli féltekén kevésbé pontosan a Dél_keresztje) adott helyen jó közelítéssel mindig ugyanott látható (mert körülbelül a Föld forgástengelyének meghosszabbításán helyezkednek el). Így a Sarkcsillag magasságának mérésével az északi szélesség azonnal adódik. Nappal a Nap delelési magasságát kell megmérni, és a dátum ismeretében (hiszen a delelés magassága egy adott helyen is változik az év során) a szélesség táblázatok segítségével meghatározható. A hullámzó tengeren nem könnyű szöget mérni: erre a célra fejlesztették ki a szextánst.
A hosszúság (kelet-nyugati irányban mért helyzet) meghatározásához azonban már szükség van a pontos idő ismeretére is. A Nap, a Hold, a csillagok és a bolygók delelésének, keltének vagy nyugtának időpontja függ a megfigyelő kelet-nyugati helyzetétől (és az időegyenlet miatt a dátumtól is). Így az égitest delelésének, keltének vagy nyugtának az időpontjának a méréséből táblázatok segítségével következtetni lehet a pillanatnyi helyzetre. Azonban 1 perc mérési hiba is negyed fok eltérést (az egyenlítő közelében több mint 25 km hibát) okoz. Egy több hónapos út során az idő ilyen pontos mérése komoly nehézségeket jelentett az újkor elején. Olyan mechanikus_órákat kellett készíteni, amelyek a tengeri út viszontagságai (hullámzás, változó hőmérséklet) mellett is minél pontosabban működtek.
A GPS
A rendszer alapelve
A GPS (Global Positioning System, globális helymeghatározó rendszer) az Egyesült Államok által eredetileg katonai célokra létrehozott és működtetett navigációs rendszer. 2000 óta a jelek kódolását megszüntették, és így a szolgáltatást bárki használhatja (korábban dekóder nélkül csak egy mesterségesen bevitt hibával torzított jel volt elérhető). Az amerikaiaktól való függés csökkentése érdekében tervezés, ill. kiépítés alatt van a – hagyományos GPS szolgáltatások mellett más információt is nyújtó – európai Galileo rendszer.
A GPS rendszernek három alapvető eleme van:
Legalább 24 pontosan meghatározott pályán keringő műhold,
3 földi állomás, melyek a műholdak pályáját ellenőrzik,
és a GPS vevőkészülékek.
A műholdak a Föld felszíne felett kb. 20 ezer km magasan, az egyenlítővel 55°-os szöget bezáró pályán keringenek. Naponta kétszer kerülik meg a Földet. A műholdakon két nagyon pontos atomóra, a GPS-jeleket kisugárzó antenna, a földi állomásokkal kapcsolatot tartó antenna, a pályajavítást elvégző hajtóművek és az energiaellátást biztosító napelemek találhatóak. A műholdak pontosan meghatározott frekvenciákon jelsorozatokat sugároznak a Föld felé.
A földi állomások radarok és nagy pontosságú GPS-vevők, melyek mérik a műholdak megadott és tényleges helyzetének különbségét, és ez alapján naponta kijavítják a műholdak pályáját. Ezen kívül ellenőrzik, és szükség esetén javítják a műholdakon lévő atomórák idejét is.
A GPS vevőben egy érzékeny, a műholdak frekvenciájára hangolt antenna veszi a műholdak jelét. A jel alapján a vevőkészülék azonosítja a műholdat, a jel kibocsátásának és beérkezésének különbségéből pedig -– a rádióhullámok fénysebességgel azonos terjedési sebessége alapján -– kiszámolja a műhold és a vevő közti távolságot. A vevőkészülék az összes műhold pályáját ismeri (ezeket az adatokat a műholdakról érkező adatok frissítik), így három műholdtól való távolság ismeretében a GPS-vevő helyzete már meghatározható. A pontos távolságméréshez azonban a vevőkészülékben is nagypontosságú (és nagyon drága) órára lenne szükség. (A rádióhullámok fénysebességgel, 3∙10
m/s sebességgel terjednek. Néhány méteres pontossághoz az időt 10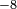
s pontossággal kell mérni!) A drága óra helyett az idő megállapításához egy negyedik műhold jelét is felhasználja a vevőkészülék.
A GPS-vevő működéséhez tehát legalább négy műhold egyidejű „látására” van szükség. Ekkor a vevőkészülék meg tudja határozni a helyzetét megadó három koordinátát (pl. a fokokban és szögpercekben megadott szélességet és hosszúságot, valamint a tengerszint feletti magasságot) és a pontos időt. A hely és az idő folyamatos mérése alapján már könnyen számolható a vevőkészülék sebessége, haladási iránya, emelkedése, a megtett út, átlagsebességek stb.
Technikai nehézségek, pontosság, hibajavítás
A helymeghatározás pontosságát csökkentik a műholdak pályahibái (az elvi pályától való kicsiny eltérés), a légkör (elsősorban az elektromosan töltött ionoszféra) zavaró hatásai, földi tárgyak (hegyek, növényzet, épületek) árnyékolása és az ezekről visszaverődő jelek.
A légkörben a rádióhullámok kicsit lassabban terjednek, mint vákuumban, ezért a jel egy kicsit később érkezik a vevőhöz (úgy, mintha távolabbról érkezne). A légkör és a rádióhullámok terjedésének elméleti modellezésével ez a hatás számításokkal részben figyelembe vehető. A légkör állapota, az ionoszféra vastagsága azonban változó. Az ebből származó hiba kiküszöbölésére több lehetőség is van.
A műholdak nem csak egy, hanem két különböző frekvencián is sugároznak. A különböző frekvenciájú jelek a diszperzió miatt más sebességgel haladnak át a légkörön, kicsiny időkülönbséggel érnek a vevőhöz. Az időkülönbségből következtetni lehet a légkör állapotára, és így a hiba jelentősen csökkenthető.
A másik fontos hibacsökkentő eljárás alapja, hogy a hiba adott időpillanatban a hely függvényében csak lassan változik. A műholdak jelét pontosan meghatározott helyen telepített vevők is veszik, és összehasonlítják a GPS-jel alapján mért pozíciót a valódival. Az így kapott javító jeleket visszajuttatják a műholdakra, amelyek azt a többi jellel együtt sugározzák (EGNOS, WAAS). Így amatőr készülékekkel a tereptől és a pillanatnyi műholdállástól függően 3-10 m pontosság érhető el. Ahol ennél nagyobb pontosságra van szükség, ott földi rádiójeleket is felhasználó, komolyabb készülékekre van szükség (differenciális GPS).
A GPS a hétköznapokban
A hajózásban és a repülésben a GPS szinte teljesen átvette a helyét a hagyományos navigációs eszközöknek. A közúti közlekedésben pedig szintén rohamos a térnyerése a papíralapú térképekkel való tájékozódás rovására. A fuvarozó cégek GPS segítségével követik nyomon a szállítmányaikat, és az ellopott járművek megtalálásában is nagy segítség a járműben elrejtett GPS-készülék. A GPS üzemzavara vagy kikapcsolása beláthatatlan következményekkel járna, ezért is fontos a független Galileo minél hamarabbi kiépítése.
Rádióadóval kiegészített kisméretű GPS vevők segítségével tanulmányozni lehet a vándormadarak és más állatok mozgását. Ugyan ennek a technikának a segítségével a tájfutó világversenyeken az erdőben futó versenyzők mozgását lehet a célban kivetített térképen élőben nyomon követni. Precíziós, földi segédállomást használó készülékekkel pedig akár néhány cm-es elmozdulások is mérhetők, ami lehetővé teszi a GPS használatát a geológiában is.
Az árak rohamos csökkenésével egyre többen használnak hobbi GPS készülékeket. Kirándulás, hegymászás közben nagy segítség, hogy sötétben, ködben is lehet tájékozódni. A készülék memóriájában rögzített nyomvonal (track) lehetővé teszi a futás, kirándulás, biciklizés vagy utazás utólagos elemzését (távok, sebességek, helyek, időpontok) és az útvonal megjelenítését térképen vagy űrfotón. A kezdetekben a készülékek elterjedésének gyorsítására kitalált GPS-es kincskereső játék (a geocaching, Magyarországon a geocaching.hu) mára több mint 1 millió ember szórakozása világszerte.
Vissza a Kísérleti fizika 1. nyitóoldalára
1. Tér és idő
3. Megmaradási törvények a mechanikában
