Investigation of High Temperature Superconductors
WIP
English Text
Superconductivity in a nutshell
Dutch physicist Heike Kamerlingh Onnes was the first to conduct experiments near absolute zero temperature, after building his helium liquefying installation. Within a short amount of time, by 1911, his low temperature measurements have led to a surprising discovery: he found that the resistance of a mercury wire below 4.19 K goes down to zero. Later, it was found that various other materials (eg. lead, tin, aluminium) behave as perfect conductors below a particular temperature. Merely two years later, in 1913, Kamerlingh Onnes was rewarded the Nobel prize for his work.
Following the discovery of superconductivity, nearly half a century needed to pass for a theoretical explanation to be formulated (J. Bardeen, L. Cooper, R. Schiffer – 1957, Nobel prize: 1972). According to the theory, the charges responsible for transporting supercurrent are electron pairs that have special properties, and move through a crystal in a manner different from single electrons. These so called Cooper pairs have been investigated experimentally (Nobel prize: 1973), which later led to the appearance of applications, such as the very high sensitivity magnetometer SQUID devices, the construction of the world's fastest "conventional" computers, or perspectives on superconducting nanostructure based quantum computers.
Since Onnes' discovery, superconductivity has continually been one of the highlighted topics of modern physics. This is shown by the fact that superconductivity-related work has resulted in Nobel prizes in 1987 and 2003 in addition to the above mentioned examples. In 1987 the prize was granted for groundbreaking work on high temperature superconductors, a work of great technical importance as it allows applications based on superconductivity at temperatures closer to liquid nitrogen's boiling temperature, a substance much cheaper and more abundant than helium. Given the appearance of such high temperature superconductors, promising potential in such applications as superconducting motors or long distance transmission lines was also a possibility. The phase transition of such superconducting materials is the focus of study in this laboratory practice.
Another phenomenon related to superconductivity is the so called Meissner effect, discovered in 1933 by Meissner and Ochsenfeld. They demonstrated that below a critical field strength value a magnetic field cannot penetrate the interior of a superconductor, and materials that are cooled down to superconductivity in the presence of finite external fields will expel magnetic fields from within them. The first property may be explained by the creation of a compensating magnetic field, arising from the induction of a persistent electric current (due to the external field changing in time), which does not decay in time within the superconductor due to its zero resistance. The second property, however, goes beyond the bounds of classical electromagnetism.
The zero electrical resistance of the superconducting state enables the creation of very high persistent currents, on the scale of 100 Amperes, by running a current through a superconducting coil, disconnecting the power supply and shorting the two ends of the coil. This current that doesn't decay with time can maintain a magnetic field of several Tesla without further power consumption. This principle is used today by magnetic levitation trains, and medical MRI machines, or the magnets of CERN's particle accelerators. In this lab practice, the persistent current will be studied in a simplified setup. Inside a superconducting ring, the magnetic flux cannot change, as that would have to result in an induced potential; this is not possible due to the zero resistance of the superconductor, which denies any voltage drop. According to this, for a superconducting ring cooled down in a magnetic field, even after the external field is stopped, the magnetic flux inside the ring will remain unchanged, sustained by the persistent current induced inside the ring.
Hungarian Text
A szupravezetésről dióhéjban
Heike Kamerlingh Onnes holland fizikus, miután megépítette hélium cseppfolyósító berendezését, elsőként végezhetett kísérleteket az abszolút nulla fokhoz igazán közeli hőmérsékleteken. Alacsony hőmérsékleti mérései rövid időn belül, 1911-ben nagyon meghökkentő felfedezéshez vezettek: azt találta, hogy egy higanyszál ellenállása 4,19 K hőmérséklet alatt zérusra csökken. Később kiderült, hogy számos anyag (pl. ólom, ón, alumínium) tökéletes vezetőként, úgynevezett szupvavezetőként viselkedik megfelelően alacsony hőmérsékleten. Kammerling Onnes munkáját már két évvel később, 1913-ban Nobel-díjjal jutalmazták.
A szupravezetés felfedezését követően közel fél évszázadot kellett várni a jelenség elméletének megszületésére (J. Bardeen, L. Cooper, R. Schiffer – 1957, Nobel-díj: 1972). Eszerint a szupravezető áramot szállító töltések különös tulajdonságokkal rendelkező elektron-párok, amelyek az egyszerű elektronoktól eltérő módon terjednek egy kristályban. Az ún. Cooper-párok viselkedésének kísérleti vizsgálata (Nobel-díj: 1973) vezetett a későbbiekben olyan alkalmazási lehetőségekre, mint a legérzékenyebb mágneses tér szenzor (SQUID) megalkotása, a világ leggyorsabb “hagyományos” számítógépeinek készítése, vagy a szupravezető nanoszerkezeteken alapuló kvantum-számítógépek perspektívája.
Onnes korai felfedezése óta a szupravezetés folyamatosan a modern fizika kiemelt témái közé tartozik. Ezt jelzi, hogy szupravezetéssel kapcsolatos elméleti vagy kísérleti munkákért a fentieken kívül 1987-ben és 2003-ban is osztottak ki Nobel-díjakat. Kiemelkedő technikai jelentőségű a magashőmérsékletű szupravezetőkért odaítélt Nobel-díj (1987), hiszen ekkor vált lehetővé, hogy a folyékony héliumnál lényegesen olcsóbb folyékony nitrogen forráspontján is elérhető legyen a szupravezetés. Az ilyen új anyagok kedvező tulajdonságai révén olyan lehetőségek is ígéretessé váltak, mint szupravezető motorok vagy távvezetékek készítése. A laboratóriumi gyakorlat keretében magashőmérsékleti szupravezető anyag szupravezető fázisátalakulását vizsgáljuk.
A szupravezetés másik kísérő jelensége az 1933-ban felfedezett ún. Meissner-effektus. Meissner és Ochsenfeld megmutatták, hogy egy kritikus érték alatt a mágneses tér nem tud behatolni a szupravezetők belsejébe, valamint a véges mágneses térben lehűtött és szupravezetővé vált anyagok az átalakulási hőmérsékletük alá hűtve kiszorítják magukból a mágneses teret. Míg az előbbi tulajdonság önmagában megmagyarázható az időben változó külső mágneses tér által keltett, és a szupravezetők nulla elektromos ellenállása miatt nem csillapodó köráramok következtében fellépő kompenzáló mágneses térrel, az utóbbi jelenség túlmutat a klasszikus elektromosságtan keretein.
A szupravezető állapotban tapasztalt nulla elektromos ellenállás lehetővé teszi, hogy egy szupravezető tekercsbe áramot vezetve, majd a tápegységet kiiktatva és a tekercs végeit rövidre zárva a tekercsben keringő, akár 100 Amperes nagyságú, időben nem csillapodó áramokkal több Tesla nagyságú mágneses tereket tartsunk fenn további külső meghajtás nélkül. Napjainkban ezt az elvet használják ki a mágnesesen lebegtetett vonatok, az orvosi MRI készülékek vagy a CERN részecskegyorsító szupravezető mágneseiben. A laboratóriumi gyakorlat keretében egy egyszerűsített elrendezésben vizsgáljuk a csillapítatlan köráramot. Egy szupravezető gyűrű belsejében nem változhat a mágneses fluxus, hiszen a fluxusváltozás hatására feszültség indukálódna, de a zérus ellenállás miatt nem eshet feszültség a szupravezetőben. Ennek megfelelően mágneses térben lehűtött szupravezető gyűrű belsejében a külső tér lekapcsolása után is bent marad, “befagy” a mágneses fluxus, amit a külső tér kikapcsolása után a gyűrűben folyó, csillapítatlan szupravezető köráram tart fenn.
Mágneses tér mérése GMR szenzorral
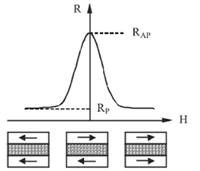
A szupravezető gyűrű belsejében felépülő vagy onnan kiszoruló mágneses teret a merevlemezek olvasófejeiben is alkalmazott mágneses tér érzékelő szenzorral mérhetjük. Az ilyen, ún. óriás mágneses ellenállást (GMR) mutató nanoszerkezetek felfedezése (1988) Albert Fert és Peter Grünberg nevéhez kötődik, akik 2007-ben Nobel-díjat kaptak felfedezésükért. A szerkezet két ferromágneses rétegből áll, amelyeket egy vékony nemmágneses réteg választ el egymástól (lásd 1. ábra, alsó panel). A felhasznált anyagok és a nemmágneses réteg vastagságának megfelelő megválasztásával elérhető, hogy külső mágneses tér hiányában a két réteg mágnesezettsége egymással ellentétes irányú legyen. Erre az elrendezésre megfelelő nagyságú külső mágneses teret kapcsolva a két réteg mágnesezettségét beforgathatjuk egymással párhuzamos irányba. A mágnesezettség párhuzamos (parallel, P) állása esetén a rétegszerkezet ellenállása lényegesen kisebb, mint az ellentétes (antiparallel, AP) beállás esetén, így külső mágneses tér alkalmazásával jelentős ellenállás-csökkenést tudunk elérni. Ezt a jelenséget hívjuk óriás mágneses ellenállásnak.
| 1. ábra. Az óriás mágneses ellenállás szemléltetése. |
A jelenséget hátterében az áll, hogy az elektromos vezetési tulajdonságok függnek attól, hogy az elektronok spinje (illetve mágneses momentuma) milyen irányban áll a ferromágneses réteg mágnesezettségéhez képest. Az elrendezés valamelyest hasonlít az optikai polárszűrőkhöz: keresztezett polárszűrőkön kevés, míg azonos állású polárszűrőkön sok fény halad át. Fontos azonban megjegyezni, hogy a GMR jelenség csak nanoszerkezetekben jelentkezik, ha a két mágneses réteget lényegesen vastagabb nemmágneses réteg választja el, akkor az elektronok mire a második rétegbe jutnak, különböző kölcsönhatási mechanizmusoknak köszönhetően már elfelejtik, hogy milyen mágnesezettségi irányú rétegből jönnek, így az ellenállás nem függ a két réteg mágnesezettségének irányától. Optikában ez annak feleltethető meg, mint ha a két polárszűrő közé egy olyan diffúz közeget helyeznénk, mely véletlenszerűen elforgatja a polarizációt.
Az elektronikai iparban a mágneses ellenálláson alapuló technológiák első és máig is legjelentősebb felhasználása a merevlemezek olvasófejéhez kapcsolódik. Ezekben az 1990-es évek elején induktív olvasófejeket alkalmaztak: a merevlemezeken mágnesesen tárolt információ kiolvasását a gyorsan forgó mágneses lemez által egy kis tekercsben indukált feszültség segítségével végezték. Az 1990-es évek közepén áttérve a magnetorezisztív technológiára először az anizotróp mágneses ellenálláson (AMR) alapuló olvasófejek terjedtek el. Az AMR fejeknek köszönhetően jelentős tárolókapacitás-növekedést sikerült elérni, azonban az AMR jelenség kis, <1 százalékos ellenállás-változása a későbbiekben komoly korlátozó tényezővé vált. A GMR jelensége ezt az értéket egy nagyságrenddel meghaladja, így az 1990-es évek vége óta a merevlemezekben a GMR jelenségén alapuló olvasófejeket használnak. Ezzel a módszerrel a merevlemezek tárolókapacitásának további jelentős növekedését lehetett elérni.
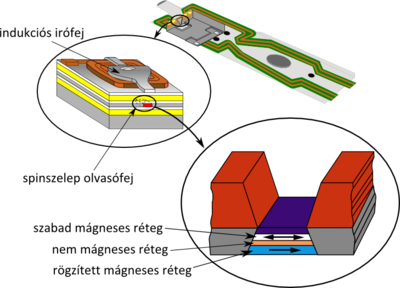
A GMR olvasófejek az ún. spin-szelep elrendezést követik. A két mágneses rétegből az egyik rögzített, nehezen elfordítható irányú mágnesezettséggel rendelkezik, míg a másik egy könnyen forgatható mágnesezettségű réteg (2. ábra). Az utóbbi réteg mágnesezettsége az olvasófej alatt forgó merevlemezen tárolt bitek mágnesezési irányának megfelelően áll be, így az információ a spinszelep ellenállásának mérésével egyszerűen kiolvasható.
| 2. ábra. Az óriás mágneses ellenállás elvén alapuló merevlemezek működése. |
Mérési feladatok
Biztonsági előírások:
- A mérések során fokozott óvatossággal kezeljük a szupravezető mintákat, mivel drága és sérülékeny eszközök.
- A szupravezető anyagok mérgezőek az emberi szervezet számára, így a mérés során ne együnk, valamint a mérések végén mossunk kezet. A szupravezető minták felületén speciális bevonat van, így szabad kézzel megfogva sem kerül szennyeződés a kezünkre, azonban fontos az elővigyázatosság.
- A folyékony nitrogénnel óvatosan bánjunk, kerüljük a kontaktust a bőrrel. A folyékony nitrogénben lehűtött tárgyakhoz ne nyúljunk szabad kézzel!
Szupravezető fázisátalakulásának mérése
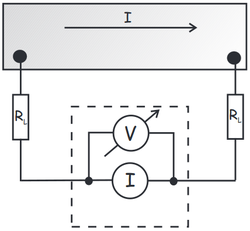
A szupravezető minta ellenállása a normál állapotban is nagyon kicsi, néhányszor tíz m nagyságú. Ezért ha két pontban mérjük az ellenállását, a mért értéket a kontaktusok ellenállása fogja dominálni, ahogy a 4.a) ábrán is látszik. Ezeket az ellenállásértékeket nem ismerjük. Ha ismernénk őket, a mért értékből kivonva akkor is csak nagyon pontatlanul tudnánk meghatározni a minta tényleges ellenállását,
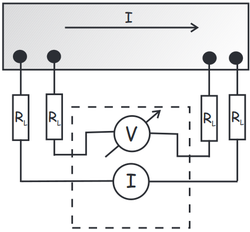
ezért egy másik módszerrel, úgynevezett négypont ellenállásméréssel végezzük a kísérletet (4.b) ábra). Ebben az elrendezésben a műszerek által mutatott feszültség és áram értékek hányadosa ténylegesen csak a minta ellenállását fogja megadni.
nagyságú. Ezért ha két pontban mérjük az ellenállását, a mért értéket a kontaktusok ellenállása fogja dominálni, ahogy a 4.a) ábrán is látszik. Ezeket az ellenállásértékeket nem ismerjük. Ha ismernénk őket, a mért értékből kivonva akkor is csak nagyon pontatlanul tudnánk meghatározni a minta tényleges ellenállását,
ezért egy másik módszerrel, úgynevezett négypont ellenállásméréssel végezzük a kísérletet (4.b) ábra). Ebben az elrendezésben a műszerek által mutatott feszültség és áram értékek hányadosa ténylegesen csak a minta ellenállását fogja megadni.
| 4. ábra. a) Ellenállás mérése két pontban. b) Ellenállás mérése négy pontban | |
1. Állítsuk össze az 5. ábrán látható mérési elrendezést!
| 5. ábra. Szupravezető pálca átalakulásának mérésére szolgáló elrendezés. |
Az összeállítás lépései:
- Csatlakoztassuk a mérőkártyát egy USB kábelen keresztül a számítógépre.
- A minta négypontellenállásának mérésére szolgáló banándugók közül a V+ és V- kivezetéseket csatlakoztassuk a GW Instek digitális multiméter feszültségmérő bemeneteire. Az I+ kivezetést egy 100
 -os ellenállással sorban kössük a mérőkártya 5 V-os kimenetére. Az I- kivezetést csatlakoztassuk a mérőkártya DGND kimenetére.
-os ellenállással sorban kössük a mérőkártya 5 V-os kimenetére. Az I- kivezetést csatlakoztassuk a mérőkártya DGND kimenetére.
- A Pt1000-es ellenálláshőmérőt szintén négypontos elrendezésben mérjük. Feszültségmérésre a mérőkártya digitális multiméter bemenetét használjuk, az áramot a mérőkártya 5V-os kimenetéről egy 1 k
 -os ellenálláson keresztül adjuk ki.
-os ellenálláson keresztül adjuk ki.
2. Írjunk mérésvezérlő programot a szupravezető minta illetve a hőmérő ellenállásának mérésére. A hőmérő hőfoktényezője alapján számítsuk át a hőmérő ellenállását hőmérsékletté. (Megjegyzés: az adatok utólagos kiértékelése során vegyük figyelembe a platina ellenálláshőmérő karakterisztikájának nemlinearitását is!)
3. A mérésvezérlő program segítségével vegyük fel a szupravezető minta négypontellenállásának hőmérsékletfüggését úgy, hogy lassan belemártjuk a mintatartót a folyékony nitrogénbe. Miután stabilizálódott a hőmérséklet a folyékony nitrogén hőmérsékletén, lassan emeljük ki a mintatartót és az asztalra téve várjuk meg, amíg felmelegszik szobahőmérsékletre. Melegedés közben is mérjük az ellenállás hőmérsékletfüggését. A mért görbék alapján határozzuk meg a szupravezető átalakuláshoz tartozó kritikus hőmérsékletet!
- Miért térnek el a hűléskor és a melegedéskor mért átalakulási hőmérsékletek egymástól?
- Milyen hibái lehetnek a hőmérséklet mérésének?
- Mekkora hibával tudjuk meghatározni a minta ellenállását? Mekkora az a legnagyobb ellenállás, amit még nullának mérünk?
Szupravezető köráram mérése
1. Állítsuk össze a mérési elrendezést az 5. ábra alapján!
| 5. ábra Szupravezető gyűrű vizsgálatának mérési elrendezése. |
Ennek menete:
- A mérőkártyáról válasszuk le az előző mérés eszközeit.
- A mágneses szenzor kék/barna kivezetését csatlakoztassuk a mérőkártya 5 V-os kimenetére, a kék-fehér/barna-fehér kivezetést a DGND kimenetre.
- A szenzor zöld/narancs és zöld-fehér/narancs-fehér kivezetéseit banándugókkal csatlakoztassuk a mérőkártya multiméter bemenetére.
- A táp kivezetéseit banánkábelekkel kössük a tekercsre. A tekercsen eső feszültség mérésére a tekercs kivezetéseit az AI 1+ és AI 1- bemenetekre is kössük rá.
2. Számoljuk ki, hogy mekkora a mágneses tér a tekercs közepén a tekercsen eső feszültség függvényében! A tekercs menetszáma és ellenállása a tekercs oldalán olvasható, a hosszát tolómérővel mérhetjük meg. A számolt mágneses tér alapján kalibráljuk a GMR szenzor feszültségjelét a mágneses tér függvényében.
3. A műanyag csipesz segítségével helyezzük a szupravezető gyűrűt az edény aljára, majd töltsünk folyékony nitrogént az edénybe. Ezután helyezzük a GMR szenzort a gyűrű közepébe, és kapcsoljunk a tekercsre körülbelül 3.5 mT mágneses térnek megfelelő feszültséget. Mit mutat a szenzor? Értelmezzük a jelenséget!
4. Vegyük ki a szenzort és a gyűrűt az edényből, az utóbbihoz használjunk a műanyag csipeszt. Várjuk meg, míg a gyűrű felmelegedik, közben öntsük vissza az edényből a folyékony nitrogént a termoszba. Ezután helyezzük vissza az üres edényt és a mintát a tekercs közepébe, majd kapcsoljunk a tekercsre ismét 3.5 mT mágneses térnek megfelelő feszültséget. Öntsünk óvatosan folyékony nitrogént az edénybe, és helyezzük vissza a mágneses szenzort. Kapcsoljuk le a tekercs által biztosított külső mágneses teret. A kikapcsolás pillanatától számítva az idő függvényében mérjük a szenzor jelét legalább 10 percen keresztül! Közben ha szükséges, pótoljuk a folyékony nitrogént. Értelmezzük a tapasztalatokat!
- A mérés alapján adjunk felső becslést a gyűrű ellenállására!
- Az előző feladatrészben számolt zérus ellenállás hibájával kalkulálva mennyi idő alatt csökken le a gyűrűben a mágneses tér nullára?
5. Várjuk meg míg elfogy a nitrogén, és felmelegszik a gyűrű. Közben mérjük a gyűrű közepében a teret.
Megjegyzés: ha precízebben szeretnénk elvégezni a mérést, akkor a GMR szenzort kalibrálni kell szobahőmérsékleten és alacsony hőmérsékleten is!
Függelék: A mérésen használt eszközök
- szupravezető pálca
- mintatartó hőmérővel
- myDAQ mérőkártya
- termosz
- folyékony nitrogén
- szupravezető gyűrű
- hungarocell edény
- tekercs
- mágneses szenzor
- műanyag csipesz
- tápegység
- banánkábelek
- csavarhúzó
- tolómérő