Termoelektromos jelenségek

A Landauer-formula tárgyalásakor láttuk, hogy egy elektródából egy egycsatornás nanovezetékbe folyó áram az elektróda Fermi-függvényének energia szerinti integrálja szerint származtatható:

$\[\frac{2}{L} \sum (-e) \cdot v_k \cdot f(\varepsilon_k) = -\frac{2}{h}\int e\cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I.\]$

Ha egy $\setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%$ transzmissziós valószínűségű szórócentrumot tartalmazó egycsatornás nanovezeték elektródái közé $\setbox0\hbox{$V$}% \message{//depth:\the\dp0//}% \box0%$ feszültséget kapcsolunk, a nanovezetékben

$\[I=\frac{2 e}{h} \cdot \int \mathcal{T}\cdot [f_1(\varepsilon)-f_2(\varepsilon)]\mathrm{d}\varepsilon\]$

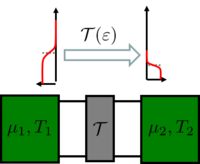
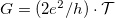áram folyik, mely alapján $\setbox0\hbox{$G=(2e^2/h)\cdot\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%$ vezetőképességet kapunk. A következőkben azt vizsgáljuk meg, hogy mi történik, ha elektródáknak nem csak a kémiai potenciálja tér el, hanem a hőmérsékletük is különböző lehet (1. ábra).

1. ábra. Különböző kémiai potenciálú és hőmérsékletű elektródák közötti $\setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%$ átmeneti valószínűségű szórócentrummal rendelkező egycsatornás nanovezeték elektromos és hőtranszport tulajdonságaira vagyunk kíváncsiak

Az elektromos áramot hasonlóan számíthatjuk az elektródák kémiai potenciál és hőmérsékletfüggő Fermi-függvényei segítségével:

$\[I=\frac{2 e}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon\]$

A termodinamikából ismert 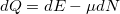$\setbox0\hbox{$dQ=dE-\mu dN$}% \message{//depth:\the\dp0//}% \box0%$ összefüggés alapján hasonlóan származtatható az elektródából a nanovezetékbe folyó 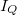$\setbox0\hbox{$I_Q$}% \message{//depth:\the\dp0//}% \box0%$ hőáram is:

$\[\frac{2}{L} \sum (\varepsilon_k-\mu) \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int (\varepsilon-\mu) \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_Q,\]$

illetve ennek megfelelően a két elektróda között folyó hőáram $\setbox0\hbox{$\mathcal{T}$}% \message{//depth:\the\dp0//}% \box0%$ transzmissziós valószínűség esetén:

$\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon.\]$

Itt fontos megjegyezni, hogy ha az első elektródából/elektródába folyó hőáramot számítjuk, akkor a fenti integrálban 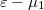$\setbox0\hbox{$\varepsilon-\mu_1$}% \message{//depth:\the\dp0//}% \box0%$. Ugyanígy számíthatnánk a 2. elektródából/elektródába folyó hőáramot, ekkor a fenti integrálban 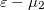$\setbox0\hbox{$\varepsilon-\mu_2$}% \message{//depth:\the\dp0//}% \box0%$ szerepelne. Mivel ez a két számolás ugyan akkora hőáramot kell, hogy adjon, így a kétféle számolás szükségszerűen ugyan arra az eredményre vezet.

Termofeszültség számolása (Seebeck-effektus)

$\[\int_{-\infty}^\infty H(\varepsilon)\cdot f(\varepsilon,\mu,T)\,\mathrm{d}\varepsilon = \int_{-\infty}^\mu H(\varepsilon)\,\mathrm{d}\varepsilon + \frac{\pi^2}{6}(kT)^2 H^\prime(\mu) + \mathrm{O} \left(\frac{kT}{\mu}\right)^4\]$

$\[I\approx\frac{2 e}{h} \cdot \int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)\,\mathrm{d}\varepsilon +\frac{2 e}{h}\frac{\pi^2}{6}(kT_1)^2 \mathcal{T}^\prime(\mu_1)-\frac{2 e}{h}\frac{\pi^2}{6}(kT_2)^2 \mathcal{T}^\prime(\mu_2)\approx \frac{2 e}{h} \cdot eV \cdot\bar{\mathcal{T}}(\varepsilon)+\frac{2 e}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot\mathcal{T}^\prime(\mu)\]$

$\[\Delta T=T_1-T_2;\ \ \ T=\frac{T_1+T_2}{2};\ \ \ \mu=\frac{\mu_1+\mu_2}{2}\]$

$\[V \big|_{I=0}=\underbrace{-\frac{\pi^2 k^2 T}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon )}{\partial \varepsilon} \bigg|_{\mu}}_{S} \cdot \Delta T\]$

$\[\frac{2}{L} \sum (-e) \cdot v_k \cdot f(\varepsilon_k) = -\frac{2}{h}\int e\cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I\]$

$\[\frac{2}{L} \sum \varepsilon_k \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int \varepsilon \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_\varepsilon\]$

$\[\frac{2}{L} \sum (\varepsilon_k-\mu) \cdot v_k \cdot f(\varepsilon_k) = \frac{2}{h}\int (\varepsilon-\mu) \cdot f(\varepsilon)\,\mathrm{d} \varepsilon \rightarrow I_Q\]$

$\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T_1)-f_2(\varepsilon,\mu_2,T_2)\right]\mathrm{d}\varepsilon\]$

$\[I_Q\approx\frac{2}{h}\frac{\pi^2}{6}(kT_1)^2\cdot\mathcal{T}(\mu) -\frac{2}{h}\frac{\pi^2}{6}(kT_2)^2\cdot \mathcal{T}(\mu) =\frac{2}{h}\frac{\pi^2 k^2}{3}\cdot\Delta T\cdot T \cdot \mathcal{T}(\mu)\]$

$\[I=G\cdot V;\ \ \ I_Q=G_Q \cdot \Delta T\]$

$\[\frac{G_Q}{G}=\mathcal{L}\cdot T;\ \ \ \mathcal{L}=\frac{\pi^2k^2}{3e^2}=2.44\times 10^{-8}\,\mathrm{W\,\Omega\,K^{-2}}\]$

$\[\frac{\kappa}{\sigma}=\mathcal{L}\cdot T\]$

$\[I_Q=\frac{2}{h} \cdot \int \mathcal{T(\varepsilon)}\cdot (\varepsilon-\mu_1)\cdot \left[f_1(\varepsilon,\mu_1,T)-f_2(\varepsilon,\mu_2,T)\right]\mathrm{d}\varepsilon\]$

$\[I_Q\approx\frac{2}{h} \cdot \underbrace{\int_{\mu_2}^{\mu_1} \mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\,\mathrm{d}\varepsilon}_{\sim (eV)^2} +\frac{2}{h}\frac{\pi^2}{6}(kT)^2\left[\overbrace{\underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime |_{\mu_1}}_{\mathcal{T}(\mu_1)}- \underbrace{\left(\mathcal{T}(\varepsilon)(\varepsilon-\mu_1)\right)^\prime|_{\mu_2}}_{\mathcal{T}^\prime (\mu_2)(\mu_2-\mu_1)+\mathcal{T}(\mu_2)}}^{2\mathcal{T}^\prime (\mu)\cdot eV}\right]\]$

$\[I_Q\approx \frac{2e}{h}\frac{\pi^2 k^2 T^2}{3}\cdot \frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu \cdot V\]$

$\[I= -\frac{2e^2}{h}\mathcal{T}\cdot V\]$

$\[\frac{I_Q}{I}\bigg|_{T_1=T_2}\approx -\frac{\pi^2 k^2 T^2}{3e}\cdot \frac{1}{\mathcal{T}}\frac{\partial \mathcal{T}(\varepsilon)}{\partial \varepsilon}\bigg|_\mu =\Pi=T\cdot S\]$