Félvezető termoelem és Peltier-elem vizsgálata
A mérés célja:
- elmélyíteni a hallgatók termoelektromos effektusokkal kapcsolatos ismereteit,
- megismertetni a hallgatókat a félvezető termoelemmel és a Peltier-elemmel (termoelektromos hűtő elemmel).
Ennek érdekében:
- összefoglaljuk a félvezető termoelemmel és a Peltier-elemmel kapcsolatos elméleti tudnivalókat,
- mérések segítségével meghatározzuk a félvezető termoelem és a Peltier-elem fontosabb jellemzőit,
- a mért Seebeck és Peltier együttható hányadosából meghatározzuk az abszolút hőmérsékletet.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
A Hőmérsékletérzékelők hitelesítése című mérés elméleti részében részletesebben foglalkoztunk a két vezetőből készült termoelemek működésével és alkalmazásával. Most az ott elmondottakra is támaszkodunk.
Termoelektromos jelenségek
A félvezető termoelem és a Peltier-elem működését termoelektromos és hőtani folyamatok határozzák meg. A termoelektromos jelenségek elektromos és hőtani folyamatok közötti kapcsolatokat adnak meg. Összefoglalónkat ezen effektusok (a Seebeck-, a Peltier-, a Thomson-effektus) és a Joule-hő ismertetésével kezdjük, majd a tisztán hőtani folyamatok leírásával folytatjuk, míg végül megvizsgáljuk ezek együttes hatását a termoelem és a Peltier-elem viselkedésére.
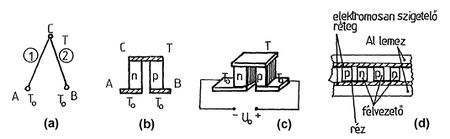
A termoelektromos jelenségek fémek esetében is fellépnek, de az effektusok sokkal erősebbek félvezetők alkalmazásakor: például egy félvezető termoelem hőfoktényezője egy nagyságrenddel nagyobb, mint egy fém termoelemé. Ezért a gyakorlatban használt Peltier-elemek (termoelektromos hűtőelemek) is félvezetőkből készülnek és a mérésen is ilyet használunk. Egy n- és p-típusú félvezetőből kialakított termoelemet mutat az (1/b ábra).
- Ha az A és B pont
 hőmérsékleten van és C pont hőmérséklete
hőmérsékleten van és C pont hőmérséklete  , (
, (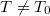 ) az A és B pont között
) az A és B pont között  feszültséget mérhetünk. Ez a Seebeck-effektus. Az effektusra jellemző az anyagtól és hőmérséklettől függő
feszültséget mérhetünk. Ez a Seebeck-effektus. Az effektusra jellemző az anyagtól és hőmérséklettől függő  állandót az egyenlettel definiáljuk.
állandót az egyenlettel definiáljuk.![\[\alpha = \left( \frac{{\rm d}U}{{\rm d}T}\right)_{T_0}\]](/images/math/3/6/4/364e5e0253bdac838e57410d28fa5841.png)
- Ha a fenti összeállításon áram folyik, az áram irányától függően a C pontban hő szabadul fel, vagy hő nyelődik el. Ez a Peltier-effektus. Az egységnyi idő alatt felszabaduló vagy elnyelt hőnek megfelelő hőteljesítmény (
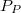 ) arányos az
) arányos az  árammal: ahol
árammal: ahol![\[P_P=\frac{{\rm d}Q}{{\rm d}t}=\pi I=\alpha TI\]](/images/math/8/e/1/8e19e4403c9d7cdfc53f61e0f8f112d0.png)
 a hő,
a hő, 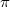 a Peltier-együttható,
a Peltier-együttható,  az abszolút hőmérséklet, míg
az abszolút hőmérséklet, míg  a Seebeck-együttható.
a Seebeck-együttható.
- Amikor
 áram folyik olyan homogén vezetőben, amelyben az áram irányába eső
áram folyik olyan homogén vezetőben, amelyben az áram irányába eső 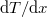 gradiens van, az áram és a hőmérséklet gradiens irányától, valamint a vezető anyagától függően hő szabadul fel, vagy nyelődik el. Ez a Thomson-effektus. Az időegység alatt a vezető egységnyi hosszúságú részében fejlődő Thomson-hő arányos az áramerősséggel és a hőmérséklet gradienssel: ahol
gradiens van, az áram és a hőmérséklet gradiens irányától, valamint a vezető anyagától függően hő szabadul fel, vagy nyelődik el. Ez a Thomson-effektus. Az időegység alatt a vezető egységnyi hosszúságú részében fejlődő Thomson-hő arányos az áramerősséggel és a hőmérséklet gradienssel: ahol![\[P_T=- \tau \frac{{\rm d}T}{{\rm d}x} I\]](/images/math/b/8/f/b8fed7328e61488504e5b110df6a8500.png)
 a vezető anyagától és a hőmérséklettől függő előjeles mennyiség, a Thomson-állandó. A Thomson-hő pozitív előjelű – azaz hő szabadul fel –, ha
a vezető anyagától és a hőmérséklettől függő előjeles mennyiség, a Thomson-állandó. A Thomson-hő pozitív előjelű – azaz hő szabadul fel –, ha  pozitív előjelű és az áram a magasabb hőmérsékletű hely felől az alacsonyabb hőmérsékletű hely felé folyik.
pozitív előjelű és az áram a magasabb hőmérsékletű hely felől az alacsonyabb hőmérsékletű hely felé folyik.
- Az árammal átjárt vezetőben hő szabadul fel: az úgynevezett Joule-hő. A Joule-törvény értelmében a teljesítmény, ha
 ellenállású vezetőn
ellenállású vezetőn  áram folyik:
áram folyik: ![\[P_J=I^2 R\]](/images/math/f/8/5/f851d9ebcaeef098ac2b7d78be385ec0.png)
- Az eszköz működésével kapcsolatos "tisztán" hőtani folyamatok közül egyedül az elem belsejében lejátszódó hővezetés hatását vesszük figyelembe. Ha a meleg oldal
 és a hideg oldal
és a hideg oldal  hőmérsékletű (
hőmérsékletű (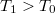 ), akkor a meleg oldalról a hideg oldal felé lejátszódó hővezetés teljesítménye: ahol
), akkor a meleg oldalról a hideg oldal felé lejátszódó hővezetés teljesítménye: ahol![\[P_v=\lambda \frac{A}{d}\left(T_1-T_0\right)\]](/images/math/9/8/b/98b12672b52c06282f9b5925504b75ac.png)
 a hővezető-képesség,
a hővezető-képesség,  az elem keresztmetszetének területe és
az elem keresztmetszetének területe és  a vastagság. A termoelemként és Peltier-elemként is használható eszköz vázlata a 1/d ábrán látható.
a vastagság. A termoelemként és Peltier-elemként is használható eszköz vázlata a 1/d ábrán látható.
Félvezető termoelem
Ha két fémből (1 és 2) termoelemet hozunk létre (1/a ábra), az A és B pontok között mérhető feszültség a C pont  hőmérséklete és az A és B pont közös
hőmérséklete és az A és B pont közös  hőmérsékletének különbségétől (
hőmérsékletének különbségétől (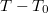 ), valamint a két fém anyagi minőségétől függ. A kapott feszültség nem függ a két fém C pontban történ összeforrasztására használt harmadik fém anyagi minőségétől. A fém termoelemhez hasonlóan, két különböző módon szennyezett félvezetőből is létrehozhatunk termoelemet. Ezek érzékenysége kb. egy nagyságrenddel nagyobb, mint a fémből készült termoelemeké. A félvezető termoelem vázlata az 1/b ábrán, perspektivikus rajza pedig az 1/c ábrán látható.
), valamint a két fém anyagi minőségétől függ. A kapott feszültség nem függ a két fém C pontban történ összeforrasztására használt harmadik fém anyagi minőségétől. A fém termoelemhez hasonlóan, két különböző módon szennyezett félvezetőből is létrehozhatunk termoelemet. Ezek érzékenysége kb. egy nagyságrenddel nagyobb, mint a fémből készült termoelemeké. A félvezető termoelem vázlata az 1/b ábrán, perspektivikus rajza pedig az 1/c ábrán látható.
A termoelem egyik jellemzője az előző részben bevezetett Seebeck-együttható, ami az l°C hőmérséklet-különbség hatására kialakuló termofeszültséget adja meg.
Az első közelítésben a termoelem üresjárási feszültségének hőmérsékletfüggése az![\[U_0=\alpha_{12}\left(T-T_0\right)\]](/images/math/8/a/3/8a36d45ed879e5f441899449647d09e2.png)
 darab p-n átmenetet tartalmaz, amelyek elektromosan sorba kapcsolódnak (1/d ábra), így feszültségük összeadódik:
darab p-n átmenetet tartalmaz, amelyek elektromosan sorba kapcsolódnak (1/d ábra), így feszültségük összeadódik: ![\[U=kU_0\]](/images/math/5/c/a/5ca23c43b7432bab2f5412f77f318ebc.png)
Az átmenetek két alumínium lemezhez csatlakoznak, jó hővezető, de elektromosan szigetelő réteggel (1/d ábra). Az alumínium lemezek közül az egyik (a meleg oldal)  hőmérsékleten, míg a másik (a hideg oldal)
hőmérsékleten, míg a másik (a hideg oldal)  hőmérsékleten van. Ilyen módon az elemek hőtani szempontból párhuzamosan kapcsolódnak.
hőmérsékleten van. Ilyen módon az elemek hőtani szempontból párhuzamosan kapcsolódnak.
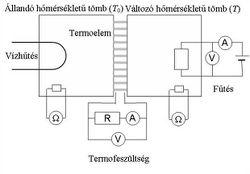
Vizsgálatainkhoz a termoelemet két hőcserélő közé helyezzük (3/a ábra). A hideg oldalhoz csatlakozó hőcserélőn (alumínium tömb) csapvizet vezetünk keresztül és ennek az oldalnak a hőmérsékletét állandó ( ) értéken tartjuk. A meleg oldalhoz csatlakozó alumínium tömbben ellenállás fűtőtest van, amit alacsony feszültségű külső áramforrás segítségével működtetünk. Így a meleg oldal hőmérsékletét változtatni tudjuk.
) értéken tartjuk. A meleg oldalhoz csatlakozó alumínium tömbben ellenállás fűtőtest van, amit alacsony feszültségű külső áramforrás segítségével működtetünk. Így a meleg oldal hőmérsékletét változtatni tudjuk.
Ha különböző  hőmérsékletek mellett megmérjük a termoelem
hőmérsékletek mellett megmérjük a termoelem  üresjárási feszültségét, az
üresjárási feszültségét, az  –
– 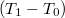 összefüggést ábrázolva egyenest kapunk. Az egyenes meredeksége a Seebeck-együttható.
összefüggést ábrázolva egyenest kapunk. Az egyenes meredeksége a Seebeck-együttható.
A termoelem fontos jellemzője a belső ellenállása. A belső ellenállást a Hőmérsékletérzékelők hitelesítése című jegyzetben leírtak (6. feladat) szerint mérhető.
Termoelemünk termikus energia hatására termel villamos energiát. Mekkora hatásfokkal teszi ezt? Erre a kérdésre a következő módon kaphatunk feleletet:
A termoelemet belső ellenállásával azonos nagyságú ellenállással terheljük. Ekkor tudjuk kivenni a maximális elektromos teljesítményt. Ehhez a meleg oldali alumínium tömböt kb. 20 W villamos teljesítménnyel felfűtjük, majd a fűtést kikapcsolva mérjük az időben csökkenő hőmérsékletet és a terhelő ellenálláson jelentkező villamos teljesítményt. Ha feltételezzük, hogy rendszerünk a környezettől jól szigetelt, akkor azt mondhatjuk, hogy a fűtött alumínium tömb által leadott hő hatására nyerünk elektromos teljesítményt. A leadott hőteljesítmény:![\[P_h=\frac{{\rm d}Q}{{\rm d}t}=cm\frac{{\rm d}T}{{\rm d}t}\]](/images/math/e/2/8/e28d4a5214ef0ca6a27ed7485adb0d04.png)
 és
és  az alumínium fajhője ill. a tömb tömege.
A fentiek alapján termoelem hatásfoka úgy állapítható meg, hogy a
az alumínium fajhője ill. a tömb tömege.
A fentiek alapján termoelem hatásfoka úgy állapítható meg, hogy a 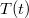 hűlési görbe vizsgált pontján meghatározzuk
hűlési görbe vizsgált pontján meghatározzuk 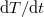 értékét és az előzőképlet alapján számítjuk a fűtőteljesítményt (
értékét és az előzőképlet alapján számítjuk a fűtőteljesítményt (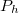 -t), miközben mérjük az ugyanezen időponthoz tartozó villamos teljesítményt:
-t), miközben mérjük az ugyanezen időponthoz tartozó villamos teljesítményt: ![\[P_v=\frac{U^2}{R}\]](/images/math/3/d/b/3db28c3ca3a2c9c387570126bec8dc47.png)
![\[\eta=\frac{P_v}{P_h}\]](/images/math/9/3/e/93e2426418e8a61098f3710c155984ad.png)
A fentiekből a hatásfok hőmérséklet-különbség függése [az 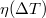 kapcsolat] is meghatározható.
kapcsolat] is meghatározható.
A termoelem 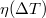 hatásfokának értékét egy adott
hatásfokának értékét egy adott 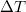 hőmérsékletkülönbségnél úgy is meghatározhatjuk, hogy az alumíniumtömböt állandó, ismert fűtőteljesítménnyel melegítjük. Miután állandósult a hőmérsékletkülönbség, akkor a fűtés teljesítménye megegyezik a
hőmérsékletkülönbségnél úgy is meghatározhatjuk, hogy az alumíniumtömböt állandó, ismert fűtőteljesítménnyel melegítjük. Miután állandósult a hőmérsékletkülönbség, akkor a fűtés teljesítménye megegyezik a 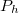 leadott hőteljesítménnyel, így a hatásfok egyszerűen meghatározható.
leadott hőteljesítménnyel, így a hatásfok egyszerűen meghatározható.
Peltier-elem
Az előzőekben áttekintett effektusok eredményeként röviden összefoglalva a vizsgált Peltier-elem belsejében a következő folyamatok játszódnak le:
- Az áram irányától függően a Peltier-effektus miatt az egyik oldalon az átmenetnél hő nyelődik el (hideg oldal,
 hőmérsékleten), másik oldalon hő szabadul fel (meleg oldal,
hőmérsékleten), másik oldalon hő szabadul fel (meleg oldal,  hőmérsékleten).
hőmérsékleten).
- A Thomson-effektus következtében a félvezető elemek anyagától (és az áramiránytól) függően az elem belsejében hő szabadul fel vagy nyelődik el. Ez a Peltier-elem két felületén egyenlő mértékű.
- A Joule-hő következtében az elem belsejében hő fejlődik. Ezt egyszerűség kedvéért úgy tekintjük, hogy egyenlő arányban jut a két felületre.
- A hővezetés eredménye egy a meleg oldalról a hideg oldal felé történő hőáramlás.
![\[P_H=\alpha T_0 I - \tau \frac{T_1-T_0}{2 d} I - \frac{I^2 R}{2} - \lambda \frac{A}{d}\left(T_1-T_0\right),\]](/images/math/4/e/1/4e1b626d553a554e0296e92b14eede75.png)
![\[P_F=\alpha T_1 I + \tau \frac{T_1-T_0}{2 d} I + \frac{I^2 R}{2} - \lambda \frac{A}{d}\left(T_1-T_0\right)\]](/images/math/f/9/5/f9567148960953b2cde1bf1060c89dc9.png)
![\[P_E=P_F - P_H=\alpha \left(T_1-T_0\right) I + \frac{\tau}{d} \left(T_1-T_0\right) I + I^2 R=U_p I\]](/images/math/f/f/6/ff654018f5ca0feb3b714427722c05d1.png)
ahol 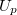 a Peltier-elem kapcsain mérhető feszültség,
a Peltier-elem kapcsain mérhető feszültség,  pedig az átfolyó áram nagysága.
pedig az átfolyó áram nagysága.
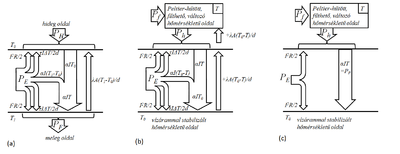
A Peltier-elem energetikai folyamatait a 2/a. ábra szemlélteti. A hőerőgépek és a hűtőgépek működése az ideális Carnot-körfolyamat segítségével közelíthető. Hőerőgépként a Carnot-gép 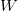 munkát végez, miközben a rendszer a magasabb
munkát végez, miközben a rendszer a magasabb  hőmérsékletű hőtartályból
hőmérsékletű hőtartályból 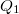 hőmennyiséget vesz fel, míg a kisebb
hőmennyiséget vesz fel, míg a kisebb  hőmérsékletű hőtartálynak
hőmérsékletű hőtartálynak 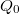 hőt ad le. Az így nyert munka
hőt ad le. Az így nyert munka 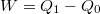 . A gép hatásfoka illetve maximális hatásfoka pedig rendre
. A gép hatásfoka illetve maximális hatásfoka pedig rendre 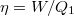 ill.
ill. 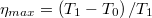 . (Így működik a termoelem.) Hűtőgépként (hőszivattyúként) a Peltier-elem fordított Carnot-gépnek tekinthető. Külső
. (Így működik a termoelem.) Hűtőgépként (hőszivattyúként) a Peltier-elem fordított Carnot-gépnek tekinthető. Külső 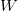 munka befektetése árán a hidegebb
munka befektetése árán a hidegebb  oldalról
oldalról 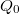 hőt von ki, míg a melegebb oldalon
hőt von ki, míg a melegebb oldalon 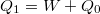 hőt ad le. A folyamat teljesítménytényezője
hőt ad le. A folyamat teljesítménytényezője 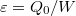 ill.
ill. 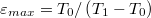 . Vegyük észre, hogy
. Vegyük észre, hogy 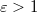 is lehet. A hatásfok ill. teljesítménytényező a megfelelő teljesítmények segítségével is kifejezhető.
is lehet. A hatásfok ill. teljesítménytényező a megfelelő teljesítmények segítségével is kifejezhető.
 hőmérséklete közel állandó), míg a másik oldal hőszigetelt és fűthető (2/b. ábra). Ennek megfelelően, a változó hőmérsékletű oldal hőháztartását az alábbi egyenlet írja le:
hőmérséklete közel állandó), míg a másik oldal hőszigetelt és fűthető (2/b. ábra). Ennek megfelelően, a változó hőmérsékletű oldal hőháztartását az alábbi egyenlet írja le: ![\[cm\frac{{\rm d}T}{{\rm d}t}=-P_h+P_f-\lambda\frac{A}{d}\left(T-T_0\right)\]](/images/math/4/9/7/4974f0d6e88567d38537a08d0fa163c0.png)
 és
és  a tömb tömege ill. fajhője,
a tömb tömege ill. fajhője, 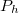 a hőszivattyúként működtetett Peltier-elem által kivont hőteljesítmény (a hővezetés figyelembe vétele nélkül),
a hőszivattyúként működtetett Peltier-elem által kivont hőteljesítmény (a hővezetés figyelembe vétele nélkül), 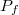 a külső fűtőellenállásból származó fűtőteljesítmény, míg a harmadik tag a Peltier-elemen keresztül hővezetéssel átjutó ismeretlen hőteljesítmény. Termikus egyensúlyban a baloldal 0, vagyis a jobboldali tagok kiejtik egymást.
a külső fűtőellenállásból származó fűtőteljesítmény, míg a harmadik tag a Peltier-elemen keresztül hővezetéssel átjutó ismeretlen hőteljesítmény. Termikus egyensúlyban a baloldal 0, vagyis a jobboldali tagok kiejtik egymást.
Legyen kezdetben 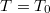 . Ha a Peltier-elemet a fűtés bekapcsolása nélkül
. Ha a Peltier-elemet a fűtés bekapcsolása nélkül 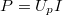 elektromos teljesítmény befektetése mellett működtetjük,
elektromos teljesítmény befektetése mellett működtetjük,  olyan értékre áll be, melynél
olyan értékre áll be, melynél 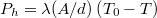 .
.  növelésével
növelésével 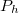 , és ezzel a hőmérséklet-különbség is nő. Mivel azonban
, és ezzel a hőmérséklet-különbség is nő. Mivel azonban 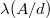 ismeretlen, a teljesítménytényező így nem határozható meg.
ismeretlen, a teljesítménytényező így nem határozható meg.
Az  teljesítménytényező meghatározásához olyan elrendezésben használjuk a Peltier-elemet, hogy a külső fűtés a 'hideg' oldalnál legyen, a 'meleg' oldalt pedig a vízhűtéssel állandó hőmérsékleten tartjuk. Ilyenkor állandó teljesítménnyel működtetve a Peltier-elemet nézzük különböző
teljesítménytényező meghatározásához olyan elrendezésben használjuk a Peltier-elemet, hogy a külső fűtés a 'hideg' oldalnál legyen, a 'meleg' oldalt pedig a vízhűtéssel állandó hőmérsékleten tartjuk. Ilyenkor állandó teljesítménnyel működtetve a Peltier-elemet nézzük különböző 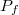 külső fűtőteljesítmény mellett a kialakuló
külső fűtőteljesítmény mellett a kialakuló 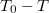 egyensúlyi hőmérséklet-különbségeket. Alkalmasan választott fűtőteljesítmény esetén a két oldal közti hőmérséklet-különbség eltűnik. Ekkor a
egyensúlyi hőmérséklet-különbségeket. Alkalmasan választott fűtőteljesítmény esetén a két oldal közti hőmérséklet-különbség eltűnik. Ekkor a 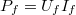 fűtőteljesítmény éppen megegyezik a Peltier-elem által a vízhűtött oldalra átszivattyúzott
fűtőteljesítmény éppen megegyezik a Peltier-elem által a vízhűtött oldalra átszivattyúzott 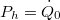 hőteljesítménnyel:
hőteljesítménnyel: 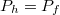 (lásd: 2./c. ábra), vagyis a teljesítménytényező az
(lásd: 2./c. ábra), vagyis a teljesítménytényező az 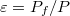 összefüggés alapján számítható, hiszen
összefüggés alapján számítható, hiszen  a fordított Carnot-gép egységnyi idő alatt bevitt külső munkája,
a fordított Carnot-gép egységnyi idő alatt bevitt külső munkája, 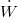 .
.
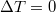 esetében nem keletkezik termofeszültség, így a Peltier-elem belső ellenállása az
esetében nem keletkezik termofeszültség, így a Peltier-elem belső ellenállása az ![\[R=\frac{U_p}{I}\]](/images/math/8/f/c/8fcf5ac5ef5c2191702231429f90bc87.png)
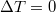 estében nincsen hővezetés (és Thomson-hő) se, így a Peltier-együttható a definiáló képlet alapján könnyen kifejezhető:
estében nincsen hővezetés (és Thomson-hő) se, így a Peltier-együttható a definiáló képlet alapján könnyen kifejezhető: ![\[\pi=\frac{P_P}{I}=\frac{P_f+\frac{1}{2}P}{I}=\frac{P_f}{I}+\frac{U_p}{2}\]](/images/math/9/f/e/9fee851f9dd934dd2abf0609f0720cdc.png)
Peltier-elem ideális meghajtása
Mérési elrendezés
A termoelem és a Peltier-elem vizsgálatához – kicsit különböző elrendezésben – ugyanazt az eszközt használjuk (3/a és 3/b ábra). A mérőeszköz két 50 g-os alumínium tömbből ill. közöttük elhelyezkedő 98 db sorba kötött p-n átmenetből áll. Az eszköznek a külső környezettel történő hőcseréjét többrétegű szigetelés akadályozza. Az egyik tömb hőmérsékletét vízhűtés rögzíti, míg a másik oldal egy tápegységgel (max. 25 V, 5 A) fűthető. A fűtőteljesítményt áram- és feszültségmérés alapján, az alumínium tömbök hőmérsékletét a Pt-hőmérők ellenállásából a![\[t(^{\circ} C)=\frac{1}{0,0039}\left(\frac{R(\Omega)}{100}-1\right)\]](/images/math/0/d/2/0d25315bcda86bb1d6a2a5b6717b0833.png)
A termoelem kimenetén mérhető a termofeszültség és a terhelő áram (3/a ábra).
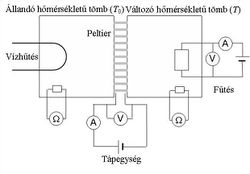
A Peltier-elem működtetéséhez egy másik tápegységet (max. 40 V, 10 A) használunk (3/b ábra). A Peltier-teljesítményt áram- és feszültségmérés alapján számítjuk.
Mérési feladatok
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
1. Határozza meg a félvezető termoelem elektromotoros erejét a hőmérséklet függvényében! Ábrázolja az elektromotoros erő – hőmérséklet-különbség összefüggést és határozza meg a Seebeck-állandót. A fűtőellenállásra kezdetben kb. 2 V, majd egyre nagyobb (max. 20 V) feszültséget kapcsolva folyamatosan fűtse a meleg oldalt, és néhány percenként olvassa le a hőmérséklet (ellenállás) és üresjárati feszültség értékeket.
- Az ellenállás alapján számított hőmérséklet:
![\[t(^{\circ} C)=\frac{1}{0,0039}\left(\frac{R(\Omega)}{100}-1\right)\]](/images/math/0/d/2/0d25315bcda86bb1d6a2a5b6717b0833.png)
2/a Határozza meg a termoelem belső ellenállását! Az első feladat utolsó fűtőteljesítményének beállított értékén folytassa a fűtést a véghőmérséklet eléréséig, és ott határozza meg a termoelem belső ellenállását.
- Emlékeztetőül: A termoelem belső ellenállásához mérni kell
- a termoelem üresjárati feszültségét (
 ),
),
- a termoelem áramát egy ismert ellenálláson keresztül (
 ). Ez az ismert ellenállás maga az árammérő is lehet, pl. 20 mA vagy 200 mA méréshatáron.
). Ez az ismert ellenállás maga az árammérő is lehet, pl. 20 mA vagy 200 mA méréshatáron.
- Az árammérő ellenállását (
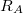 , ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. Az ellenállásmérőt egyszerűen rákötjük a – más áramkörbe ezalatt be nem kötött! –, megfelelő méréshatárra beállított árammérőre.
, ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. Az ellenállásmérőt egyszerűen rákötjük a – más áramkörbe ezalatt be nem kötött! –, megfelelő méréshatárra beállított árammérőre.
-
 ,
,  és
és 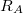 ismeretében az
ismeretében az 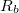 belső ellenállás számolható.
belső ellenállás számolható.
- a termoelem üresjárati feszültségét (
- Milyen méréshatárra állított árammérővel terheli a termoelemet? Miért?
- Mekkora az árammérő belső ellenállása ezen a méréshatáron?
- Hogyan fejezhető ki
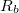 a mért mennyiségek segítségével?
a mért mennyiségek segítségével?
2/b Határozza meg a termoelem hatásfokát!
A belső ellenállás meghatározása után kapcsoljon a belső ellenállással kb. megegyező ellenállást a termoelem kivezetéseire. Ehhez használjon ellenállásdekádot.
A terhelés hatására csökkenni fog a kialakult hőmérséklet-különbség. Várja meg, amíg a hőmérséklet-különbség egy új értéken állandósul. Mérje meg ekkor a termoelem kimenetén (a terhelő ellenálláson) a kapocsfeszültséget. Számítsa ki a terhelő ellenálláson leadott teljesítményt (a hasznos teljesítményt) és – a fűtőteljesítmény ismeretében – a termoelem hatásfokát.
3. Mérje meg 2,4 A Peltier-áram esetén (a fűtőtest kiiktatásával) a kialakuló hőmérséklet-különbséget!
- A tápegységet áramgenerátoros üzemmódban használja!
- Az áramerősséget a kimenetek rövidre zárása mellett állítsa be!
- A feszültséglimitet (üresjáratban) 3 V-ra állítsa be!
- Hameg multiméterekkel mérje a Peltier-áramot és (a Peltier-elem kivezetésein) a Peltier-feszültséget!
Mérje a hőmérsékletet 10 percig és a függelékben megadott összefüggések illesztésével határozza meg a kialakuló max. (állandósult) hőmérséklet-különbséget!
- A változó hőmérsékletű (a Peltier-elemmel hűtött) oldal hőmérsékletét számítógépes adatgyűjtő segítségével mérje az idő függvényében.
4. Mérje rögzített Peltier-áram és különböző fűtőteljesítmények mellett a kialakuló hőmérséklet-különbségeket és ábrázolja ezeket! Peltier-áram: 2,4 A, fűtőteljesítmények: 3-11 W között 3-4 értéken mérve. A Peltier-elemet működtető tápegységet az előző feladathoz hasonlóan áramgenerátoros üzemmódban használja, és minden esetben írja fel az egyensúly közelében kialakuló feszültségértékeket is! Mérje a hőmérsékletet esetenként 10 percig és a függelékben megadott összefüggések illesztésével határozza meg a fenti teljesítményeknél kialakuló max. hőmérséklet-különbségeket!
- A változó hőmérsékletű (a Peltier-elemmel hűtött, a fűtőellenállással viszont fűtött) oldal hőmérsékletét számítógépes adatgyűjtő segítségével mérje az idő függvényében.
- Figyelem! A Peltier-feszültség (állandó Peltier-áram mellett) a hőmérséklet-különbség változásával változik. Mi ennek az oka?
5. Az állandósult hőmérséklet-különbség – fűtőteljesítmény kapcsolat alapján számítsa ki a Peltier-elem teljesítmény-tényezőjét és belső ellenállását!
- Ehhez ábrázolja az állandósult hőmérséklet-különbséget a fűtőteljesítmény függvényében, és egyenesillesztéssel határozza meg, milyen fűtőteljesítménynél lenne nulla a hőmérséklet-különbség.
- A nulla hőmérséklet-különbséghez tartozó Peltier-feszültséget interpolálással határozza meg.
- A Peltier-elem belső ellenállására kapott eredményét hasonlítsa össze a termoelem belső ellenállásával.
6. Határozza meg a Peltier-együtthatót! A Seebeck-együttható és a Peltier-együttható ismeretében számítsa ki a  abszolút hőmérsékletet!
abszolút hőmérsékletet!
- A termikus egyensúly beállása viszonylag hosszú időt igényel. Ezért a
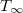 véghőmérséklet meghatározásánál kihasználjuk, hogy a fűthető oldal hőmérsékletének (
véghőmérséklet meghatározásánál kihasználjuk, hogy a fűthető oldal hőmérsékletének ( ) időbeli változása jó közelítéssel exponenciális jellegű: ahol
) időbeli változása jó közelítéssel exponenciális jellegű: ahol![\[T(t)=T_\infty+\left(T_0-T_\infty\right)\exp(-t/\tau)\]](/images/math/7/1/0/71024640507374036f40f0050f2fa061.png)
 a hőmérséklet kezdeti értéke, míg
a hőmérséklet kezdeti értéke, míg  a hőmérséklet-változás karakterisztikus ideje.
a hőmérséklet-változás karakterisztikus ideje.
7. Határozza meg a zérus külső fűtőteljesítmény mellett elérhető maximális hőmérsékletkülönbséget!
- A korábbi feladatokban kapott Peltier-együttható és a belső ellenállás felhasználásával számolja ki, hogy mekkora áramnál várja a maximális hőmérsékletkülönbséget.
- Állítson be a kiszámított áramértéktől 0.5 A-rel kisebb meghajtóáramot és várja meg, míg a hőmérséklet közel állandó értékre áll be. Jegyezze fel a hőmérsékletet és utána emelje az áram értékét, majd ismét rögzítse az állandósult hőmérsékletet.
- A fenti módon minél pontosabban próbálja meg kísérletileg meghatározni a maximális hőmérsékletkülönbséget és a hozzá tartozó áramot!