Fotoeffektus vizsgálata uj

A mérés célja:

• Igazolni, hogy a fotoelektronok kinetikus energiája, illetőleg a vele arányos lezáró feszültség független a fény intenzitásától,
• a $\frac{h}{e}$ arány meghatározása méréssel.

Ennek érdekében:

• Megmérjük egy vákuumfotodióda lezárási feszültséget
  • különböző intenzitású fénynél
  • különböző hullámhosszú fénynél

Elméleti összefoglaló

A fotoeffektus

A külső fényelektromos hatás alapjelensége: ha egy fémlemezre fény esik, a lemezből elektronok lépnek ki. E jelenség vizsgálata néhány olyan eredményre vezetett, melyeket a fény folytonos hullámelméletével nem lehet megmagyarázni. Ezek a következők:

• Az elektronok csak akkor lépnek ki, ha a fény frekvenciája nagyobb egy, az illető fémre jellemző határfrekvenciánál. A klasszikus szemlélet szerint azonban a 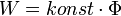$W = konst\cdot\Phi$ feltételnek megfelelő sugárzási intenzitás minden frekvencián biztosítható.
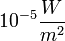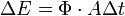• Megfelelő fényfrekvencia esetén az elektronok kilépése akármilyen gyenge fény hatására azonnal (10^-9 s-on belül) bekövetkezik. (A kísérletek során használt fémeknél a kilépési munka 10^-19 J nagyságrendű, az elektron által „lefedett” terület, ahonnan energiát gyűjthet ~ 10^-19m² , egy átlagos megvilágítást feltételezve, ami $~10 ^{-5} \frac{W}{m^2}$, a $\Delta E=\Phi \cdot A \Delta t$ alapján 10⁵ s , ~ 28 óra lenne a folyamathoz szükséges idő.)
• A kilépő elektronok száma arányos a megvilágítás erősségével, de energia eloszlásuk független attól. A maximális mozgási energia a fény frekvenciájának lineáris függvénye, a klasszikus számítások szerint ez nem lineáris.

E kvalitatív tapasztalatok kvantitatív magyarázatát Albert Einstein adta meg azzal, hogy Planck kvantumhipotézisét a fényjelenségekre is kiterjesztette. Feltételezte, hogy a Planck-féle 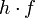$h \cdot f$ energiacsomag nem csak a sugárzó oszcillátor diszkrét energiaváltozásait adja meg, hanem a sugárzási térben is 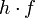$h \cdot f$ adagokban van jelen az energia. A fényenergia diszkrét energiaadagokban terjed. Ezek a fotonok. Tehát egy foton energiája:

 

$\[E = h \cdot f \]$

(1)

ahol $\setbox0\hbox{$h$}% \message{//depth:\the\dp0//}% \box0%$ a Planck-féle állandó, $\setbox0\hbox{$f$}% \message{//depth:\the\dp0//}% \box0%$ pedig a sugárzás– esetünkben a fény – frekvenciája. Az elektronok kilépése csak akkor indulhat meg, ha a beeső fotonok energiája legalább az elektronok kötési energiájával egyenlő. A kilépés feltétele tehát:

 

$\[ h \cdot f \geq W = h \cdot f_{0} \]$

(2)

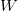ahol $\setbox0\hbox{$W$}% \message{//depth:\the\dp0//}% \box0%$ az elektron kötési energiája, az úgynevezett kilépési munka, $\setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0%$ pedig a fémre jellemző küszöbfrekvencia. Általános esetben:

 

$\[ h \cdot f = W + \frac{1}{2} m v^2 \]$

(3)

vagyis a foton energiatöbblete a kilépő elektron kinetikus energiájaként jelenik meg. Nagyobb fényintenzitás több fotont, tehát több kilépő elektront jelent. Ilyen módon magyarázatot nyert a külső fényelektromos jelenség valamennyi felsorolt sajátsága.

1.ábra

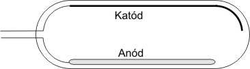
A fényelektromos jelenség legelterjedtebb gyakorlati alkalmazása a fotocella vagy fotodióda, amelyet mi is alkalmazunk mérésünkben. A fotocella egy légritkított üvegcső, melynek egyik oldalán a belső felületére felvitt fémréteg képezi a katódot, a vele szemben elhelyezett dróthurok pedig az anód (1.ábra). Mint a (3) egyenletből látható, a határfrekvencia esetétől eltekintve a kilépő elektronok kinetikus energiával is rendelkeznek, ami feszültségmentes tér esetén elegendő ahhoz, hogy az anódig repüljenek, ezért 0 anódfeszültség esetén is mérhető bizonyos – igen kicsi – áram.

Ahhoz, hogy a fotocella tetszőleges megvilágítás ellenére teljesen árammentes legyen, akkora ellenteret kell az anód és a katód között létesíteni, mely a legnagyobb energiájú elektronokat is meggátolja az anód elérésében. Az árammentesség feltétele tehát:

 

$\[ e U_{0} = \frac{1}{2} m v^2_{max} \]$

(4)

ahol $\setbox0\hbox{$e$}% \message{//depth:\the\dp0//}% \box0%$ az elektron töltése,$\setbox0\hbox{$U_0$}% \message{//depth:\the\dp0//}% \box0%$ pedig a lezáró feszültség. Mérőberendezésünkben (a továbbiakban: mérőegység) a fotoelektródok és a hozzájuk kapcsolódó elektronikus erősítő jól meghatározott kapacitást jelentenek. A fotoáram hatására ez a kapacitás elektromosan feltöltődik mindaddig, amíg potenciálja el nem éri az $\setbox0\hbox{$U_0$}% \message{//depth:\the\dp0//}% \box0%$ lezáró feszültséget. A mérőegység kimenetére kapcsolt feszültségmérővel ezt az $\setbox0\hbox{$U_0$}% \message{//depth:\the\dp0//}% \box0%$ feszültséget közvetlenül tudjuk mérni. A (3) és (4) egyenletekből $\setbox0\hbox{$U_0$}% \message{//depth:\the\dp0//}% \box0%$-ra a következő kifejezést kapjuk:

 

$\[ U_{0} = \frac{h}{e} f - \frac{W}{e} \]$

(5)

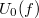Az $\setbox0\hbox{$U_0(f)$}% \message{//depth:\the\dp0//}% \box0%$ függvény egy egyenes egyenlete. Az egyenes meredeksége a $\frac{h}{e}$ állandó.

Fénykibocsátó dióda (LED)

Félvezető p-n átmenet tulajdonságai - e/k állandó meghatározása

LED nyitófeszültségének meghatározása

Diffrakció

A tapasztalat szerint egy akadály mellett elhaladó fénysugár az akadályoknál részben elhajlik, behatol az árnyéktérbe is. Ez a diffrakció (fényelhajlás) jelensége. A jelenséget a "Huygens-Fresnel-elv" segítségével lehet meg-magyarázni: a Huygens-Fresnel-elv alapján a hullámfelület minden pontja elemi hullámforrásnak tekintendő, és ezeknek az egymással koherens elemi gömbhullámoknak az interferenciája szabja meg a tér egy pontjában a fényhatást.

4. ábra

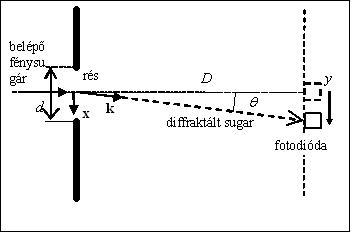
Példaképp vizsgáljuk meg az optikai rés esetét. A rés egy átlátszatlan felületen kialakított keskeny, a fény hullámhosszával összemérhető szélességű, hosszú nyílás. Világítsuk meg a rést egy koherens, párhuzamos fénynyalábbal (legegyszerűbben egy lézer fényével). A fény a résen áthaladva elhajlik. A réstől távol elhelyezett ernyőn a résből kiinduló elemi hullámok interferenciája alakítja ki a diffrakciós képet. A diffrakciós képet – az intenzitást a hely függvényében - egy fotodióda mozgatásával könnyen meg lehet mérni (4. ábra).

A k hullámszámvektor irányában a relatív intenzitást a Fourier-integrál segítségével lehet kiszámítani. Az intenzitás arányos az integrál abszolút értékének négyzetével:

$\[ I(\pmb{k}) = \left \lvert \int_{-\infty}^{\infty} e^{\pmb{kx}i}f(\pmb{x})d\pmb{x} \right \rvert^2. \]$

A kifejezésben

$\[|\pmb{k}| = k = \frac{2\pi}{\lambda},\]$

$\[\pmb{kx} = kx \sin \theta \approx kx\theta \; (\theta\ll1), \]$

$\[ f(x) = \begin{cases} \frac{1}{d} \; \mathrm{ha} \; x \in \left[-\frac{d}{2};\frac{d}{2}\right] \\ 0\; \mathrm{ha} \; x \notin \left[-\frac{d}{2};\frac{d}{2}\right]. \end{cases} \]$

Felhasználva, hogy

$\[ y = D \mathrm{tg} \theta \approx D\theta \; (\theta<<1), \]$

és elvégezve az integrálást

$\[ I(y) = \left( \frac{\lambda D}{\pi yd} \right)^2\sin^2\left( \frac{\pi yd}{\lambda D} \right).\]$

5. ábra

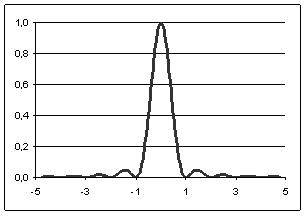
A diffrakciós kép az 5. ábrán látható. A vízszintes tengely 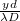$\setbox0\hbox{$\frac{yd}{\lambda D}$}% \message{//depth:\the\dp0//}% \box0%$ egységekben van skálázva. Az intenzitás az 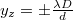$\setbox0\hbox{$y_z=\pm\frac{\lambda D}{d}$}% \message{//depth:\the\dp0//}% \box0%$ helyen válik először zérussá. Az két zérushely közti távolság (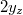$\setbox0\hbox{$2y_z$}% \message{//depth:\the\dp0//}% \box0%$) és a $\setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0%$ távolság mérésével a $\setbox0\hbox{$\lambda$}% \message{//depth:\the\dp0//}% \box0%$ hullámhossz ismeretében a $\setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0%$ résszélesség, $\setbox0\hbox{$d$}% \message{//depth:\the\dp0//}% \box0%$ ismeretében pedig a $\setbox0\hbox{$\lambda$}% \message{//depth:\the\dp0//}% \box0%$ hullámhossz meghatározható.

Meglepő módon a rés „inverzének”, egy vékony akadálynak (pl. hajszál) a diffrakciós képe ugyanilyen, így ezzel a módszerrel vékony drótok, hajszálak, stb. átmérője is mérhető. Bonyolultabb optikai struktúrák (például két vagy több párhuzamos rés) esetén a diffrakciós kép hasonlóan kiszámítható, csak 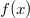$\setbox0\hbox{$f(x)$}% \message{//depth:\the\dp0//}% \box0%$ kifejezését kell ennek megfelelően módosítani.

A diffrakciós kép alapján következtetni lehet az optikai struktúrára. Ha az intenzitás kifejezésében ismernénk az abszolútértékjelen belüli kifejezést, akkor inverz Fourier-transzformációval meg lehetne határozni a diffrakciós képet létrehozó struktúrát. A mérés alapján azonban csak az intenzitást (az abszolút érték négyzetét) ismerjük, így nem teljesen egyértelmű a számítás.

A másik lehetőség az, hogy a diffrakciós kép alapján megsejtjük (vagy más információk alapján tudjuk), hogy körülbelül milyen optikai struktúra hozta létre a diffrakciós képet (például néhány egyforma, párhuzamos rés); majd paraméteresen kiszámítjuk a feltételezett struktúra diffrakciós képét, végül a paramétereket addig változtatjuk, amíg a számított és a mért diffrakciós kép a legjobban egyezik egymással.

Méréshez használt eszközök (2.ábra)

• Mérőegység (a fotodiódát és az elektronikát tartalmazó doboz)(3.ábra és 4.ábra)
• Higanygőzlámpa, hűtő- és védőburában
• Digitális feszültségmérő (multiméter)
• Lépcsős szürke fényszűrő, áteresztőképessége:100, 80, 60 40, 20%
• Sárga és zöld színszűrők
• Optikai rács és lencse együttese, a továbbiakban együtt: rács-lencse
• Stopperóra.

A mérőberendezés

A rács a higanygőzlámpa fényét monokromatikus spektrumvonalakra bontja. Mind az első, mind a második rendben jól megfigyelhetők az alábbi spektrumvonalak:

szín	hullámhossz
sárga	578 nm
zöld	546 nm
kék	436 nm
ibolya1	405 nm
ibolya2	365 nm

Ha a zöld vagy a sárga vonallal dolgozunk, használjuk a megfelelő színszűrőt, hogy a rácseltérítés folytán magasabb eltérítési rendekből átfedő ultraibolya fényt kiszűrjük!

2.ábra: A mérési elrendezés. Bal oldalon a fotocella háza, a fehér felületen jól látható a belépő rés. Jobb oldalon a higanygőz lámpa háza és az állítható pozíciójú rács-lencse.

3.ábra: A fotocella háza a kezelői felülettel és a belépő réssel.

4.ábra: A nyitott fotocellaház. Középen a fotocella fehér árnyékoló csőben. Csak a két, téglalap alakú fekete felületen jut fény a katódra.

A mérés menete

• Kapcsolja be a higanygőzlámpát. Hagyja legalább 10 percig bemelegedni. Ezalatt ellenőrizze, hogy a fényforrás, a rács-lencse és a dióda egy magasságban legyenek. Kapcsolja be a mérő egységet, és az erre szolgáló (kék) csatlakozókon feszültségmérővel ellerőrizze a tápfeszültséget adó telepek feszültségét. (Legalább 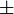$\pm$6 V szükséges a helyes működéshez. A készülék azért elemes (akkumulátoros) táplálású, mert ez biztosítja a leginkább zajmentes tápellátást.
• A bemelegedési idő után a lámpa egy kiválasztott vonalát a mérőegység forgatásával állítsa a fehér takaró lemezen lévő nyílásra. Forgassa el a mérőegységen lévő fényárnyékoló hengert, hogy láthatóvá váljék a doboz belsejében a fotodióda előtt lévő maszk és rajta az ablak. Erre az ablakra fókuszálja a spektrumvonalat a rács-lencse mozgatásával. Győződjön meg róla, hogy ugyanaz a spektrumvonal fókuszálódik a belső maszk nyílásán, mint amelyik a külső lemez nyílására esik! Ezt a mérőegység kis elforgatásával lehet szabályozni. Ezután fordítsa a helyére a fényárnyékoló hengert.
• Minden mérés előtt nyomja be a mérőegységen levő piros nullázó gombot! Ezzel kisüti az elektronikai rendszerben keletkezett feltöltődést; így biztosíthatjuk azt, hogy csak a kiválasztott spektrumvonal által keltett fotóáram következtében létrejött potenciált mérjük.

Mérési feladatok

1. Helyezze a lépcsős intenzitásszűrőt a fehér takaró lemez nyílása elé! A szűrő mágnesesen rögzíthető. Amikor színszűrőt is használ, azt erősítse a maszkra, és a színszűrő elé helyezze a lépcsős szűrőt. Csatlakoztassa a feszültségmérőt a mérőegység kimenetére. (2V vagy 20 V-os méréshatárt használjon.) Az eredményt mV pontosan olvassa le.  A sárga, zöld és kék színeknél mérje meg a lezáró feszültséget a lépcsős szűrő valamennyi fokozatában! A 20%-os fokozatnál a feszültség beállása már elég lassú, ekkor a következőképpen járjon el: előbb hagyja 1-2 percig állandósulni az értéket, majd nullázzon, és az imént elért értéknél 2mV-al kisebb feszültség eléréséig mérje a beállási időt. Jegyezze fel a feszültséget és az időt is és ismételje meg a mérést még négyszer. A sárga és a zöld színnél ne felejtse el használni a megfelelő színszűrőt! Az eredményeket táblázatban rögzítse. Mire lehet következtetni belőlük?
2. Mérje meg mind az öt hullámhossznál a beállási időt. A beállási időt az előző pontban leírt módszerrel állapítsa meg. A sárga és a zöld színnél ne felejtse el használni a megfelelő színszűrőt! A lépcsős szűrő használatával csak azokat a beállításokat mérje végig, amikor a beállási idő legalább négy másodperc.Végezze el a mérést a rács másodrendbeli vonalai közül a három legjobban látszóval is. Rögzítse táblázatban az eredményeit. Milyen különbség van az első- és másodrendben végzett mérések között? Miért?
3. Ábrázolja grafikusan a 2. feladatban kimért 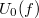$\setbox0\hbox{$U_0(f)$}% \message{//depth:\the\dp0//}% \box0%$ kapcsolatot! Határozza meg $\frac{h}{e}$ értékét és a kilépési munkát!