Hőmérsékletérzékelők hitelesítése
A mérés célja:
- három elterjedten alkalmazott hőmérsékletérzékelő: az ellenállás-hőmérő, a termisztor és a termoelem bemutatása.
Ennek érdekében:
- ismertetjük az ellenállás-hőmérő, a termisztor és a hőelem működésének alapelvét, valamint az alkalmazásukkal kapcsolatos fontosabb tudnivalókat,
- kimérjük az érzékelőket jellemző ellenállás – hőmérséklet, ill. feszültség – hőmérséklet kapcsolatokat,
- meghatározzuk az érzékelők viselkedését leíró függvények paramétereit.
Tartalomjegyzék |
Elméleti összefoglaló
Az anyagok jellemzői általában függenek a hőmérséklettől. Elvben bármely hőmérsékletfüggő tulajdonság felhasználható hőmérő készítésére. Ennek megfelelően a hőmérsékletmérő eszközök széles skáláját fejlesztették ki. A gyakorlat során a laboratóriumokban leggyakrabban használt hőmérők kerülnek bemutatásra: az ellenállás-hőmérő, a termisztor és a termoelem. Az előbbi kettőnél az elektromos ellenállás hőmérsékletfüggését használjuk ki, míg az utóbbinál termofeszültségét.
Ellenállás-hőmérő ellenállásának hőmérsékletfüggése
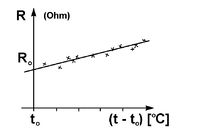
A fémes anyagok ellenállása az
![\[R = R_0 [ 1 + \alpha (T-T_0)]\]](/images/math/f/f/5/ff5528ea7539ded75b17855193e53f46.png)
kifejezéssel közelíthető, ahol  és
és 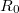 a
a  ill.
ill.  hőmérsékletekhez tartozó ellenállás értékek,
hőmérsékletekhez tartozó ellenállás értékek,  pedig az anyagtól függő hőmérsékleti tényező (1. ábra).
pedig az anyagtól függő hőmérsékleti tényező (1. ábra).  ,
, 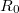 ,
,  és
és  ismeretében a hőmérséklet közvetlenül számítható.
ismeretében a hőmérséklet közvetlenül számítható.
Termisztor ellenállásának hőmérsékletfüggése
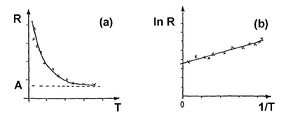
A félvezető anyagok ellenállása jól közelíthető az
![\[R = A e^\frac{B}{T}\]](/images/math/a/5/a/a5a893aed90894212418488a33ed1a75.png)
kifejezéssel (2/a ábra), ahol  a
a 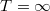 értékhez tartozó ún. maradékellenállás, és
értékhez tartozó ún. maradékellenállás, és 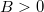 a félvezető anyagára jellemző állandó (
a félvezető anyagára jellemző állandó (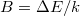 , ahol
, ahol 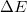 a félvezető tiltott sáv szélessége,
a félvezető tiltott sáv szélessége,  pedig a Boltzmann-állandó).
pedig a Boltzmann-állandó).
A kifejezés természetes alapú logaritmusát véve
![\[\ln R = \ln A + \frac{B}{T}\]](/images/math/9/d/f/9df783f3783f90437279b3e291270c98.png)
Ha tehát a mért ellenállás értékek logaritmusát 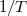 függvényében ábrázoljuk egyenest kapunk (2/b ábra), melynek tengelymetszetéből ill. meredekségéből
függvényében ábrázoljuk egyenest kapunk (2/b ábra), melynek tengelymetszetéből ill. meredekségéből  és
és 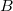 meghatározható.
meghatározható.
Ellenállás-hőmérők és termisztorok összehasonlítása
Az ellenállás-hőmérő és a termisztor ellenállása függ a hőmérséklettől. Az előbbi esetben az elektronok mozgékonyságának csökkenése miatt az ellenállás növekszik a hőmérséklettel. Ezzel szemben a termisztor ellenállása csökken, mivel a hőmérséklet emelkedésével nő a töltéshordozók koncentrációja. A két érzékelő jellemzőit a következő táblázatban hasonlítjuk össze:
| Tulajdonság | Ellenállás-hőmérő | Termisztor |
|---|---|---|
| Hőfoktényező | kicsi, 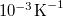 |
nagy, 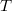 -függő -függő
|
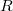 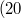 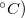
|
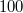 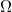 |
k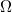 nagyságrendű nagyságrendű
|
| Stabilitás | jó | gyengébb |
| Reprodukálhatóság | jó | gyengébb |
| Karakterisztika | lineáris | exponenciális |
| Tömeg | > termisztor | < ellenállás-hőmérő |
| Hőtehetetlenség | > termisztor | < ellenállás-hőmérő |
| Ár | > termisztor | < ellenállás-hőmérő |
| Hőmérséklet tartomány | -183-tól 630 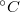 -ig -ig |
-60-tól 150 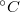 -ig -ig
|
| Anyaga | Pt, Cu, Ni, ötvözetek | különféle félvezetők |
A hőelem (termoelem)
Két különböző fém érintkezésekor a két fém között elektromos feszültség mérhető. Ez a feszültség az ún. kontaktpotenciál, melynek nagysága az érintkező fémek anyagi minőségétől és az érintkezési pont hőmérsékletétől függ.
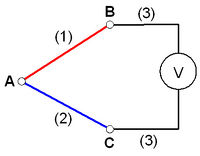
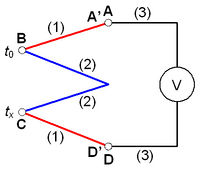
Ha a 3. ábrán látható kapcsolást három különböző [(1)-es, (2)-es, és (3)-as jelzésű] fémből alakítjuk ki, de minden pont azonos hőmérsékleten van, akkor a voltmérőn nem jelentkezik feszültség. Amennyiben valamelyik fém-fém átmenet (A, B vagy C pontok) hőmérséklete megváltozik, akkor viszont feszültség mérhető, melynek értéke arányos a hőmérséklet változással. Tehát, ha az A átmenet hőmérsékletét kívánjuk mérni, akkor a másik két átmenet (B és C pont) hőmérsékletét állandó értéken – a hitelesítés hőmérsékletén – kell tartani, ekkor a voltmérővel az A pont hőmérsékletének megváltozásával arányos feszültség mérhető. A többi pont hőmérsékletének állandó értéken tartása azért fontos, mert ellenkező esetben a fellépő kontaktpotenciál változások meghamisíthatják a mérést. Ezen nehézségeket a két összekapcsolt termoelemből álló ún. termopár (4. ábra) segítségével küszöbölhetjük ki.
A termopárt alkotó kontaktusok (B és C) az (1) és (2) anyagokat kötik össze, míg a (3) anyagból készült elvezető huzalok az A és a D pontokon kapcsolódnak a termopárhoz.
Először a termopáron kialakuló feszültséggel – vagyis az A’ és D’ pontok között fellépő feszültséggel foglalkozunk [A’ és D’ az (1) anyagban, az A és D pontok közelében levő két pont]. Ha B és C hőmérséklete különböző, vagyis 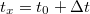 , akkor az A’ és D’ pontok között megjelenő feszültség arányos hőmérsékletkülönbséggel.
, akkor az A’ és D’ pontok között megjelenő feszültség arányos hőmérsékletkülönbséggel.
![\[U_{A^\prime B^\prime}=U_{12}(t_0+\Delta t)-U_{12}(t_0)=\alpha_{12}\Delta t\]](/images/math/1/7/f/17f9d5175c7afddf804bb435d989c070.png)
ahol az indexben levő számok a termoelemet alkotó anyagokra utalnak, és kihasználtuk, hogy a szembe kapcsolt termoelemekre 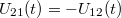 . A lineáris közelítés szűk hőmérséklet-tartományban illetve kisebb pontossági igények esetén alkalmazható. Szélesebb hőmérsékleti intervallumban további állandók bevezetése szükséges:
. A lineáris közelítés szűk hőmérséklet-tartományban illetve kisebb pontossági igények esetén alkalmazható. Szélesebb hőmérsékleti intervallumban további állandók bevezetése szükséges:
![\[U_{A^\prime B^\prime} = \alpha_{12}\Delta t + \beta_{12}\Delta t^2 + ... \]](/images/math/4/6/e/46ec50c24021bfc0708b73bf97b65819.png)
A lineáris összefüggés szerint a termopár kimenetén a B és C pontok közti hőmérsékletkülönbséggel arányos feszültség jelenik meg. Ha tehát hőmérőként kívánjuk használni, akkor az egyik átmenetet ismert hőmérsékleten kell tartani. A vonatkoztatási hőmérséklet általában 0 °C, ami olvadó jég segítségével könnyen előállítható és tartható. (A pontosság növelése érdekében célszerű desztillált vízből készíteni a jeget.) Ennél a kapcsolásnál tehát a hőmérsékletmérés a B és a C pontoknál levő átmenetek segítségével történik. A mérőműszernél (E és F pontok), valamint az elvezető huzalok csatlakozási pontjainál (A és D) azonban elkerülhetetlenül további "járulékos" termoelemek alakulnak ki. Ezek – az A’ és D’ pontoktól a kijelzőig terjedő – "járulékos" termoelemek páronként azonos anyagból állnak. [Például az A és a D pontokon az (1) és a (3) jelű anyagból.] Így a keletkezett termofeszültségek szembekapcsolódnak. Mérés közben tehát csak arra kell ügyelni hogy ezen átmeneteknek páronként (A-nak D-vel és E-nek F-el) azonos legyen a hőmérséklete. Ez a feltétel aránylag könnyen teljesíthető az átmenetek közötti jó termikus kapcsolattal.
Hitelesítés
A hitelesítés jelen esetben az érzékelők hőmérséklet – ellenállás ill. hőmérséklet – termofeszültség függvényeinek meghatározását jelenti. A mérésnél a hőmérséklet-érzékelőket olajjal töltött dupla falú üvegedénybe (hőcserélőbe) helyezzük egy-egy "hiteles" higanyos hőmérővel együtt (termopár esetében csak az egyik termoelem kerül olajfürdőbe, a másik víz-jég keverékbe merül). Az olajfürdő hőmérsékletét az üvegedény falában áramoltatott, termosztáttal szabályozott hőmérsékletű víz segítségével állítjuk be.
A higanyos hőmérő A különböző eszközök hőtehetetlensége miatt fellépő hiba kiküszöbölése érdekében a mérést növekvő és csökkenő hőmérséklet mellett is el kell végezni. (Pontosabb méréseket lehetne végezni állandósult hőmérsékleten (stacioner állapotban), de a mérési gyakorlaton nincs idő a hőmérsékleti egyensúly beálltát minden hőmérsékleten megvárni.)
Az ellenállásokat lehet Wheatstone-híddal, a feszültségeket pedig kompenzációs módszerrel is mérni. A mérési gyakorlaton azonban a méréseket digitális multiméterrel fogja végezni.
Mérési feladatok
1. Állapítsa meg az ellenállás-hőmérő és a termisztor ellenállásának, valamint a hőelem termofeszültségének hőmérsékletfüggését a hőmérséklet növekedése közben! A méréseket multiméterrel végezze! A hőmérsékletet a szobahőmérséklettől kb. 60 °C-ig változtassa!
2. Végezze el a feladatot csökkenő hőmérséklet mellett is!
3. Mérési eredményeit ábrázolja diagramon!
4. Az ellenállás-hőmérő és a termoelem vizsgálata során kapott mérési pontokra illesszen egyenest! Határozza meg az érzékelők paramétereit és adja meg hibájukat!
5. A termisztoron végzett mérés eredményeit ábrázolja 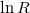 –
– 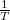 formában! A kapott pontokra illesszen egyenest, határozza meg a termisztor A és B paramétereit és adja meg a hibájukat!
formában! A kapott pontokra illesszen egyenest, határozza meg a termisztor A és B paramétereit és adja meg a hibájukat!
6. Mérje meg a hőelem belső ellenállását! A termoelem és a félvezető termoelem belső ellenállásához mérni kell
a) a termoelem üresjárati feszültségét (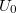 )
)
b) a termoelem áramát egy ismert ellenálláson keresztül ( ).
).
Ez az ismert ellenállás maga az árammérő is lehet, pl. 200 mA méréshatáron. Az árammérő ellenállását (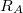 , ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. (Az ellenállásmérőt egyszerűen rákötjük a – természetesen más áramkörbe ezalatt be nem kötött –, megfelelő méréshatárra beállított árammérőre.)
Ezután a termoelem
, ami természetesen függ a méréshatártól) egy ellenállásmérő segítségével lehet megmérni. (Az ellenállásmérőt egyszerűen rákötjük a – természetesen más áramkörbe ezalatt be nem kötött –, megfelelő méréshatárra beállított árammérőre.)
Ezután a termoelem 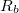 belső ellenállása a Kirchhoff-törvények alapján számolható.
Vegye figyelembe a huzalok ellenállását is!
belső ellenállása a Kirchhoff-törvények alapján számolható.
Vegye figyelembe a huzalok ellenállását is!