Lock-in programozás, kvarcszenzor vizsgálata

A mérés célja

A mérés célja a későbbi Szupravezetés c. laboratóriumi gyakorlat során is használt Stanford Research Systems SR830 típusú digitális lock-in erősítő használatának és programozásának megismerése, egy atomi erő mikroszkópokban is használt kvarc szenzor vizsgálata ill. termikus zaj jelenségének tanulmányozása a lock-in erősítő segítségével.

Ennek érdekében először gyakorló mérésként párhuzamos LC kör rezonancia görbéit vesszük fel, majd hasonló elrendezésben a kvarc oszcillátor éles rezonanciáját vizsgáljuk. Végül ellenállások termikus zajának méréséből határozzuk meg az abszolút hőmérsékletet.

Bevezetés: termikus zaj szilárdtestekben

Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség "zaja" több információt hordoz a rendszerről mint maga a várható érték. A mérési gyakorlaton az egyik legalapvetőbb zajformát, az ún. termikus zajt tanulmányozzuk. A termikus zaj véges hőmérsékleten jelentkezik a különböző állapotok betöltésének termikus fluktuációi miatt. Egy fermionikus rendszerben egy állapot betöltési száma n=0,1 lehet. A betöltési szám várható értéke a Fermi függvény,

$\[\left< n \right> =f=\frac{1}{\mathrm{e}^{\frac{\epsilon-\mu}{k_B T}}+1}.\]$

A betöltési szám szórásnégyzete:

$\[\left< \left(n-\left<n \right> \right)^2\right)=\left< n\right> -\left< n \right> ^2=f(1-f)=-k_B T\frac{\mathrm{d}f}{\mathrm{d}\epsilon},\]$

ahol kihasználtuk, hogy fermionokra 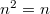$\setbox0\hbox{$n^2=n$}% \message{//depth:\the\dp0//}% \box0%$. A kifejezést energia szerint kiintegrálva (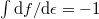$\setbox0\hbox{$\int \mathrm{d}f/\mathrm{d}\epsilon =-1$}% \message{//depth:\the\dp0//}% \box0%$) rögtön látszik, hogy a termikus zaj arányos a hőmérséklettel.

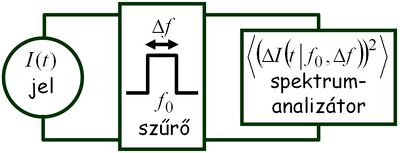
A zaj mértékének pontos megadásához először definiálni kell a zaj mérésére használt mennyiséget. Egy zajmérés kísérleti megvalósítása a következő ábrán szemléltethető:

1. ábra

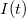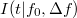A mért $\setbox0\hbox{$I(t)$}% \message{//depth:\the\dp0//}% \box0%$ jelből kiszűrjük az $\setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0%$ frekvencia körüli $\setbox0\hbox{$\Delta f$}% \message{//depth:\the\dp0//}% \box0%$ sávszélességű tartományt, és az így kapott $\setbox0\hbox{$I(t|f_0,\Delta f)$}% \message{//depth:\the\dp0//}% \box0%$ jel szórásnégyzetét vizsgáljuk egy spektrumanalizátorral. Megfelelően keskeny frekvenciasávot alkalmazva a mért szórásnégyzet arányos lesz a frekvenciasáv szélességével, és az arányossági tényezőt nevezzük a zaj spektrális sűrűségének:

$\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]$

Megmutatható hogy a zaj spektrális sűrűsége nem más, mint a áram-áram korrelációs függvény Fourier transzformáltjának a kétszerese. A zaj pontos definícióját megismerve a termikus zaj értékét a fluktuáció-disszipáció tétel alapján adhatjuk meg, mely egy rendszer egyensúlyi fluktuációi és az egyensúlyból kitérített rendszer lineáris válaszfüggvénye között teremt összefüggést. Elektromos áram esetén az ez egyensúlyi fluktuáció nem más mint az áramzaj, a lineáris válaszfüggvény pedig a külső feszültségre adott válasz, vagyis a vezetőképesség. Így egy rendszer áramzaja:

$\[S_I(f)=2hf\cdot \coth{\left( \frac{hf}{2k_B T}\right) }\cdot G.\]$

Így alacsony frekvencián (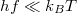$\setbox0\hbox{$hf\ll k_B T$}% \message{//depth:\the\dp0//}% \box0%$) az áramfluktuációk termikus zaja:

$\[S_I=4k_B TG.\]$

Hasonlóképpen a feszültségzaj:

$\[S_V=4k_B TR.\]$

Látjuk, hogy a termikus zaj segítségével "csupán" feszültségmérés alapján meghatározhatjuk egy rendszer abszolút hőmérsékletét. Persze a precíz zajmérések komoly méréstechnikai kihívást jelentenek, hiszen nanovoltos vagy még kisebb feszültségek fluktuációját kell pontosan mérni. Ennek ellenére a termikus zaj mérésének komoly metrológiai jelentősége van, hiszen számos módszerrel mérhetünk precízen hőmérsékletváltozást, de az abszolút hőmérsékletet nem könnyű meghatározni. A jelenleg érvényes hőmérsékletstandardok mind ún. másodlagos hőmérők, melyek nem alapvető fizikai törvény hanem megfelelő kalibráció alapján mérik az abszolút hőmérékletet. (A szobahőmérséklet körüli széles tartományban pl. platina vékonyréteg ellenálláshőmérőt használnak standardként.) A termikus zaj mérése alapvető fizikai állandók (Boltzmann állandó + elektron töltés) alapján vezeti vissza a hőmérsékletmérést feszültségmérésre, így a hőmérsékletstandardok kalibrálásának egyik alapvető módszere.

A termikus zaj mellett még két fontos zajtípusról érdemes megemlékezni. Az egyik a szennyezők és rácshibák véletlen mozgásából adódó ún. 1/f zaj, mely alacsony frekvenciákon dominál, és a nevét is a zajsűrűség tipikus frekvenciafüggéséről kapta. A másik az elektrontöltés kvantáltságából adódó ún. sörét zaj, melynek a lényege egy egyszerű példán szemléltethető: Képzeljünk el egy elektronhullámot, mely áthalad egy T transzmissziós valószínűségű nyalábosztón. Az áthaladt töltés értéke T valószínűséggel 1 és 1-T valószínűséggel 0,így az áthaladt töltés T várható értéke körül T(1-T) szórásnégyzetű fluktuációt tapasztalunk. Ezt az elemi folyamatot több elektronra általánosítva megmutatható, hogy a sörétzaj nagysága a rendszerre kapcsolt feszültséggel arányos. A fenti példából érezhető, hogy a sörétzaj kisméretű rendszerekben válik fontossá, ahol egyszerre csak kevés elektron vesz részt a vezetésben.

Mérési feladatok

1. Áramgenerátoros meghajtással vegyük fel a mellékelt párhuzamos LC kör impedanciáját a frekvencia függvényében, határozzuk meg a rezonancia-frekvenciát, a kapacitás az induktivitás ill. az induktivitás soros ellenállásának az értékét. A mért görbét hasonlítsuk össze az elméleti várakozásokkal. A méréshez írjunk számítógépes programot, mely GPIB porton kommunikál a műszerrel. A program adott számú lépésben logaritmikus skálán változtassa a frekvenciát egy megadott kezdő és végfrekvencia között, és vegye fel a bemeneten mért jel X és Y komponensét a frekvencia függvényében. Figyeljünk az időállandó helyes beállítására!

2. Az 1. feladatban készült mérőprogrammal vegyük fel a mellékelt kvarc oszcillátor rezonancia görbéjét feszültséggenerátoros meghajtást használva (a rezonancia frekvencia környékén nagyobb pontossággal!). Ennél a mérésnél a pontosabb frekvenciabeállítás érdekében jelforrásként egy Agilent ??? függvénygenerátort használjunk. A Lock-In generátorát az Agilent függvénygenerátorhoz szinkronizáljuk, a kvarc oszcillátorra a Lock-In kimenetéről adjuk ki a jelet. Az oszcillátor meghajtásához 1:100 osztót használjunk a Lock-In

3. Mérjük meg a mellékelt 0 -os (piros), 3.3 k-os (zöld) és 10 k-os (kék) ellenállások zaját (X noise, Y noise) a frekvencia függvényében. 10 Hz és 100 kHz tartományban. Határozzuk meg azt a frekvenciatartományt, ahol az alacsonyfrekvenciás 1/f zaj már elhanyagolható. Határozzuk meg a különböző frekvenciákon mért zajértékek várható értékét és annak hibáját. A mért eredmények alapján határozzuk meg a hőmérsékletet és annak hibáját. Az összes mérést ugyan olyan lock-in beállítás mellett végezzünk, különösen figyeljünk a megfelelő időállandó és méréshatár megválasztására. Használjunk 12dB/Oct ill. Low Noise beállításokat.