Sztatikus mágneses mező vizsgálata
Szerkesztés alatt!
A mérés célja
- a Helmholtz-tekercs mágneses terének vizsgálata és az Ampére-féle gerjesztési törvény kísérleti igazolása.
Ennek érdekében:
- megismerkedünk a mágneses térerősség mérésére szolgáló magnetorezisztív szenzorral, és az Universal Lab Interface (ULI) adatgyűjtő rendszerrel;
- feltérképezzük a mágneses térerősség komponensei-nek helyfüggését a Helmholtz-tekercs körül.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Egyes sztatikus mágnességgel kapcsolatos jelenségek (pl. az, hogy bizonyos vasércek a kisméretű vasdarabokat magukhoz vonzzák) már az ókorban ismertek voltak. A Föld mágneses terét évezredek óta használjuk tájékozódásra. Ezen mérés keretében állandó mágneses terek vizsgálatával foglalkozunk.
Szemben a Naprendszerünk hasonló méretű bolygóinak többségével, a Föld erős mágneses térrel rendelkezik, amely a Föld belsejében található anyag/töltés áramlásokkal hozható kapcsolatba. A Föld mágneses tere fontos szerepet játszik a földfelszín nagyenergiás kozmikus részecskékkel szembeni védelmében (1. ábra), és jelenléte alapvető lehetett a földi élet kialakulása szempontjából is.
A földmágneses tér eloszlása a Föld felszínén első közelítésben olyan, mintha egy 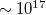 Vsm momentumú dipólus helyezkedne el a Föld közepe táján, melynek tengelye hozzávetőleg a
Vsm momentumú dipólus helyezkedne el a Föld közepe táján, melynek tengelye hozzávetőleg a 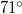 É,
É, 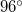 NY ill.
NY ill. 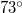 D,
D, 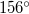 K pontoban metszi a felszínt. A súlypontjában felfüggesztett mágnestű (feltéve, hogy nincsenek a környezetében mágneses vagy mágnesezhető anyagok ill. áramjárta vezetők) a Föld
K pontoban metszi a felszínt. A súlypontjában felfüggesztett mágnestű (feltéve, hogy nincsenek a környezetében mágneses vagy mágnesezhető anyagok ill. áramjárta vezetők) a Föld 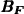 mágneses terének (mágneses indukciójának) irányába áll be.
mágneses terének (mágneses indukciójának) irányába áll be.
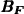 -et általában a mágneses elhajlás vagy deklináció szögével (térerősség vektoron átmenő függőleges ún. mágneses meridiánsík és az adott helyen átmenő földrajzi meridiánsík vagy hosszúsági kör által bezárt szög), ill. a lehajlás vagy inklináció szöge (
-et általában a mágneses elhajlás vagy deklináció szögével (térerősség vektoron átmenő függőleges ún. mágneses meridiánsík és az adott helyen átmenő földrajzi meridiánsík vagy hosszúsági kör által bezárt szög), ill. a lehajlás vagy inklináció szöge (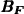 -nek a vízszintessel bezárt szöge), valamint a horizontális intenzitás (
-nek a vízszintessel bezárt szöge), valamint a horizontális intenzitás (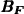 vízszintes vetülete) segítségével adják meg, melyekkel kifejezhető a teljes intenzitás (a vektor abszolút értéke) és a vertikális intenzitás (a függőleges komponens).
vízszintes vetülete) segítségével adják meg, melyekkel kifejezhető a teljes intenzitás (a vektor abszolút értéke) és a vertikális intenzitás (a függőleges komponens).
A Föld mágneses tere időfüggő. Napi, havi és éves periódusú változások egyaránt megfigyelhetők. A mágneses sarkok lassan vándorolnak (2. ábra).
A mozgó elektromos töltés (így az elektromos áram is) mágneses teret kelt. Az  áram és
áram és 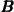 mágneses tere közötti kapcsolatot (a Biot-Savart törvény mellett) az Ampére-féle gerjesztési törvény írja le:
mágneses tere közötti kapcsolatot (a Biot-Savart törvény mellett) az Ampére-féle gerjesztési törvény írja le:
![\[ \mu_0 I = \oint \pmb{B}d\pmb{s},\]](/images/math/d/7/1/d71984a62003d4482791126422a4c209.png)
ahol 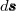 az ívelem vektor.
az ívelem vektor.
A két  távolságban levő
távolságban levő  sugarú tekercsből álló ún. Helmholtz-tekercs viszonylag homogén mágneses teret hoz létre, melynek a tekercsek tengelyében középen vett erőssége:
sugarú tekercsből álló ún. Helmholtz-tekercs viszonylag homogén mágneses teret hoz létre, melynek a tekercsek tengelyében középen vett erőssége:
![\[ B = 8\mu_0 \frac{NI}{\sqrt{125}R} ,\]](/images/math/5/b/5/5b5fa693b98ee1c4a04dd6c344434b24.png)
ahol 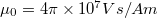 a vákuum mágneses permeabilitása,
a vákuum mágneses permeabilitása,  a tekercsen átfolyó áram (A),
a tekercsen átfolyó áram (A),  pedig a tekercsek menetszáma. Ezt az elrendezést használjuk a későbbiekben a fajlagos elektrontöltés mérésénél is.
pedig a tekercsek menetszáma. Ezt az elrendezést használjuk a későbbiekben a fajlagos elektrontöltés mérésénél is.
A mágneses teret sokféle módon lehet mérni. Egyik lehetőség a Hall-effektuson alapuló mérőeszköz: Ha egy félvezető kristályt, melyen áram folyik át, a  sűrűségű áram irányára merőleges mágneses térbe helyezünk, akkor a
sűrűségű áram irányára merőleges mágneses térbe helyezünk, akkor a ![\setbox0\hbox{$[\pmb{j} \times \pmb{B}]$}% \message{//depth:\the\dp0//}% \box0%](/images/math/f/b/1/fb1913ac0382fd647dd1a0ba285ef14a.png) nagyságú Lorentz-erő hatására a töltéshordozók kitérnek az áramsűrűségre és a mágneses térre merőleges irányba. Ezáltal a kristály oldalsó felületei annyira feltöltődnek, hogy a létrejövő ellenfeszültség a mágneses tér eltérítő hatását éppen kiegyenlíti. Ez a Hall-effektus. A fellépő keresztirányú Hall-feszültség
nagyságú Lorentz-erő hatására a töltéshordozók kitérnek az áramsűrűségre és a mágneses térre merőleges irányba. Ezáltal a kristály oldalsó felületei annyira feltöltődnek, hogy a létrejövő ellenfeszültség a mágneses tér eltérítő hatását éppen kiegyenlíti. Ez a Hall-effektus. A fellépő keresztirányú Hall-feszültség 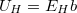 (ahol
(ahol  a kristály szélessége,
a kristály szélessége, 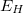 pedig a felületi töltések által létrehozott elektromos tér) a töltéshordozók koncentrációjával hozható kapcsolatba: Stacionárius állapotban
pedig a felületi töltések által létrehozott elektromos tér) a töltéshordozók koncentrációjával hozható kapcsolatba: Stacionárius állapotban 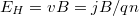 , ahol
, ahol  a töltéshordozó töltése,
a töltéshordozó töltése,  pedig a töltéshordozó koncentrációja. Az
pedig a töltéshordozó koncentrációja. Az 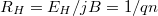 mennyiséget Hall-együtthatónak nevezzük. Ez független a mozgékonyságtól, kizárólag a töltéskoncentráció határozza meg. Negatív Hall-együttható elektronvezetést, pozitív együttható pedig lyukvezetést jelent.
mennyiséget Hall-együtthatónak nevezzük. Ez független a mozgékonyságtól, kizárólag a töltéskoncentráció határozza meg. Negatív Hall-együttható elektronvezetést, pozitív együttható pedig lyukvezetést jelent.
A mérési gyakorlaton a mágneses tér mérését Philips KMZ10B típusú magnetorezisztív szenzor segítségével végezzük.
A magnetorezisztív szenzor mágneses vékonyrétegekből készül, melyben a mágneses momentumok zérus külső tér esetén a vékonyréteg geometriája által meghatározott preferált irányba állnak be. Külső mágneses tér hatására a momentumok elfordulnak a preferált irányhoz képest, aminek következtében megváltozik a vékonyréteg ellenállása.
A mérőberendezés és összeállítása
Magnetorezisztív szenzor
A Philips KMZ10B típusú szenzor 4 darab, hídkapcsolásban elhelyezett magnetorezisztív vékonyrétegből áll (3. ábra). A híd két szemközti csúcsára 5 V tápfeszültséget kötünk, és a másik két szemközti csúcs között mérjük a feszültséget. Zérus mágneses térben a híd kiegyenlített, így a kimeneten zérus feszültség látható. Véges mágneses térben (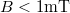 ) a térrel arányos, tipikusan mV-os nagyságrendű jelet tapasztalunk. A szenzor a kivezetésekkel szemközti oldalon, a 3. ábrán jelölt irányban méri a mágneses teret. A mérésnél 2 darab, egymásra merőlegesen elhelyezett szenzort használunk, így a Helmholtz-tekercs terének egyszerre mérhetjük az X és Y komponensét.
) a térrel arányos, tipikusan mV-os nagyságrendű jelet tapasztalunk. A szenzor a kivezetésekkel szemközti oldalon, a 3. ábrán jelölt irányban méri a mágneses teret. A mérésnél 2 darab, egymásra merőlegesen elhelyezett szenzort használunk, így a Helmholtz-tekercs terének egyszerre mérhetjük az X és Y komponensét.
Adatgyűjtés
A Helmholtz-tekercs terének feltérképezéséhez egy pozícionáló asztal áll rendelkezésre (4. ábra), mely a tekercs vízszintes felezősíkjában való pozíciót két (X és Y irányú) ellenállás huzalon való feszültségosztással elektromos jellé alakítja.
A szenzorok jelének ill. az elmozdulás X és Y koordinátáinak mérését egy 10-pólusú csatlakozó blokkon keresztül végezhetjük. Jelforrásként egy, az 5. ábrán látható Hameg 8142 típusú tápegységet használunk, mely egy fix (5 V, max. 2 A) és két változtatható kimenettel rendelkezik (0-30 V, 0-1 A).
Az egyik változtatható kimenetről kössön 5 V feszültséget a két pozícióérzékelésre használt ellenálláshuzal végei közé. A pozícióérzékelő csúszkák feszültségjelét kösse a csatlakozóblokk X és Y jelű csatlakozópárjaira (A föld-pontot kösse össze az ellenálláshuzalok negatív pontjaival). Az X és Y jelű csatlakozópárokra kötött jelet a megfelelő 5-pólusú DIN csatlakozókkal kösse az ULI interface DIN1 és DIN2 bemenetére. A mérés a számítógépen futó LoggerPro program segítségével történik.
A tápegység másik változtatható kimenetét használja áramgenerátorként a Helmholtz-tekercs meghajtására.
A Hameg tápegység fix 5 V-os kimenetét használja a két mágneses tér szenzor tápfeszültségeként (csatlakozó blokk: „B sensor input”). A mágneses tér X és Y komponensével arányos feszültségjelet a csatlakozóblokk 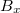 és
és 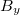 jelzésű kimenetein mérheti. Mivel itt mV-os nagyságrendű feszültségek jelentkeznek, ezért a számítógépes regisztráláshoz először erősítésre van szükség. Ehhez használja a 2 darab Vernier differenciális erősítő modult ± 20 mV-os méréshatárban. Az erősítők jelét számítógéppel regisztrálja az ULI interface DIN3 és DIN4 bemenetein keresztül. Mivel az ULI interface csak pozitív feszültségeket tud regisztrálni, a differenciális erősítővel viszont bipoláris jelet akarunk mérni (± 20 mV), az erősítő a kierősített jelhez még hozzáad egy DC offsetet is. Így zérus mágneses térben kb. 1,7 V-os offset feszültséget mérünk, és az ettől vett pozitív és negatív irányú eltérés arányos a mágneses tér nagyságával.
jelzésű kimenetein mérheti. Mivel itt mV-os nagyságrendű feszültségek jelentkeznek, ezért a számítógépes regisztráláshoz először erősítésre van szükség. Ehhez használja a 2 darab Vernier differenciális erősítő modult ± 20 mV-os méréshatárban. Az erősítők jelét számítógéppel regisztrálja az ULI interface DIN3 és DIN4 bemenetein keresztül. Mivel az ULI interface csak pozitív feszültségeket tud regisztrálni, a differenciális erősítővel viszont bipoláris jelet akarunk mérni (± 20 mV), az erősítő a kierősített jelhez még hozzáad egy DC offsetet is. Így zérus mágneses térben kb. 1,7 V-os offset feszültséget mérünk, és az ettől vett pozitív és negatív irányú eltérés arányos a mágneses tér nagyságával.
Adatgyűjtésre az Universal Lab Interface (ULI) egység szolgál, ami egy 12 MHz-en működő SAB A-P, 8032 processzort tartalmaz 256 byte RAM-mal, négy 8-bites porttal és három 16-bites időzítővel. Az adatforgalmat kontrolláló rutinokat egy 16 kB-os EPROM tartalmazza. Az ULI-ban található 12-bites analóg-digitál konverter feszültség bemenete 0-5,12 V-os, konverziós idő 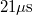 , maximális mintavételezési frekvencia 32 kHz. A számítógép felé soros (RS232) adatforgalmat biztosít (maximum boad rate: 38,4 k). Bemenetek: 2 darab moduláris telefon csatlakozó, 4 darab 5 tűs DIN csatlakozó, és 2 darab sztereo „jack” csatlakozó.
, maximális mintavételezési frekvencia 32 kHz. A számítógép felé soros (RS232) adatforgalmat biztosít (maximum boad rate: 38,4 k). Bemenetek: 2 darab moduláris telefon csatlakozó, 4 darab 5 tűs DIN csatlakozó, és 2 darab sztereo „jack” csatlakozó.
Adatfeldolgozás és megjelenítés
Az adatfeldolgozás és megjelenítés az Origin program segítségével történik. Itt csak a térerősség/vektor térképek elkészítését tárgyaljuk.
Az X irányú mágneses tér komponens ábrázolása: Importálja be a mágneses teret tartalmazó fájlt egyszeres ASCII fájlként. Törölje az időt és az Y irányú mágneses teret (DIN4) tartalmazó oszlopokat. Definiálja X, Y és Z oszlopként a DIN1, DIN2 és DIN3 bemeneteken érkezett adatokat. Jelölje ki a Z oszlopot. Konvertálja az adatait mátrixszá (Edit/Convert to Matrix/Random XYZ,  mátrix, Search Radius = 2, Smoothness = 0.8, Gridding Method = Weighted Ave). Ennek birtokában a Mátrix fejlécére kattintva megjelenő 3DPlot menüpont kijelölése után többféle háromdimenziós ábrázolási módból választhat. A mért adatokat az alábbiak szerint ábrázolja:
mátrix, Search Radius = 2, Smoothness = 0.8, Gridding Method = Weighted Ave). Ennek birtokában a Mátrix fejlécére kattintva megjelenő 3DPlot menüpont kijelölése után többféle háromdimenziós ábrázolási módból választhat. A mért adatokat az alábbiak szerint ábrázolja:
- 3D Color Map Surface (3D színes térkép felület, ld. 6. ábra)
- Countour B/W Lines+Labels (szintvonalas ábra, a szintértékek megjelölésével, ld. 7. ábra).
A fentieket végezze el az Y irányú komponensre is. (Ekkor a DIN1, a DIN2 és a DIN4 bemenetek érkezett adatokat kell használni.)
A vektor-diagram esetében az előbbiekben létrehozott mátrixokat alakítsa vissza adatlappá (Edit/Convert to Worksheet/XYZ Columns/X Constant 1st). Hozzon létre olyan új adatlapot, melynél az A és B oszlopokban az X és Y koordináták (a vektorok kezdőpontjai) találhatók, míg a C és D oszlopokat (a vektorok végpontjai) úgy töltse fel, hogy az ábrázolt nyilak iránya és hossza a mágneses térerősség XY síkbeli irányát és nagyságát mutassa.
Definiálja ezután az A és C oszlopokat X oszlopként, a B és D oszlopokat pedig Y oszlopként. Jelölje ki az A, B, C és D oszlopokat. A Plot/Vector XYXY utasítással ábrázolva vektordiagramot kap (8. ábra).