Optikai heterodin detektálás
Tartalomjegyzék |
Szerkesztés alatt!
Elméleti összefoglaló
A hullám fogalma – a fény mint hullám
A fény, mint ismeretes, az elektromágneses tér hullámjelensége. Jellemző rezgési frekvenciája a 1014 Hz körüli tartományba esik. Az a fizikai mennyiség, amelynek terjedését egyszerűen fénynek nevezzük, az elektromos és mágneses térerősség. Tehát a fényben az elektromos és a mágneses tér változásai terjednek. Tekintsünk egy, a tárgyalás szempontjából egyszerű, lineárisan polarizált harmonikus síkhullámot. A síkhullám elnevezés onnan ered, hogy az azonos térerősségű pontok egy adott pillanatban egy síkon helyezkednek el. A síkhullám kifejezése:
![\[E\left( {{\bf{r}},t} \right) {{=}} {E_0}\cos \left( {\omega t - {\bf{kr}}} \right)\]](/images/math/6/0/b/60b98f9ce1b43f8beac900bce40ea117.png)
ahol E0 az elektromos hullám amplitúdója, k a hullámszám vektor,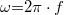 
az elektro-mágneses hullám körfrekvenciája, „f” pedig a frekvenciája. Egyszerű megfontolásokból a hullám terjedési sebessége k-val és 
-val kifejezhető:
![\[{{c = \frac{\omega }{\left| k \right|}}}\]](/images/math/5/d/4/5d492d4631dcb1bb6a6bcf00487e759c.png)
A „k” helyett a gyakorlatban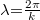 
-t szokás használni, amelyet hullámhossznak nevezünk. Így az egyenlet ismertebb alakjában 
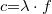. Az (1) egyenletből látszik 
szemléletes jelentése is: azt a k vektor irányában mért legkisebb távolságot jelenti, amely szerint a térerősség periodikusan változik.
Doppler-effektus
Tegyük fel, hogy az (1) szerinti monokromatikus síkhullámot egy „K” koordináta-rendszerben írtuk fel. Ha ezt a síkhullámot a K-hoz képest v(t) pillanatnyi sebességgel mozgó K' rendszerből figyeljük, akkor a hullám K-beli frekvenciájától különböző frekvenciájú hullámot fogunk észlelni. Válasszuk úgy a K és K' rendszert, hogy -ban az origók egybe essenek. Ekkor a K-beli koordinátát K'-beli koordinátákkal kifejezhetjük:
![\[{\bf{r}} = \int\limits_0^t {{\bf{v}}(\tau ){\rm{d}}\tau } + {\bf{r'}}\]](/images/math/5/1/e/51e96aacb29da120e8de44a781c4b6bd.png)
(3)
Ezt beírva az (1) egyenletbe, a hullám K'-beli alakját nyerjük:
![\[E\left( {{\bf{r'}},t} \right) = {E_0}\cos \left( {\varphi ({\bf{r'}},t)} \right) = {E_0}\cos \left( {\omega t - {\bf{k}} \cdot \int\limits_0^t {{\bf{v}}(\tau ){\rm{d}}\tau } - {\bf{k}} \cdot {\bf{r'}}} \right) \]](/images/math/b/5/3/b536ce6f20faf757d9ad7d2d7c3bdb0f.png)
(4)
Definíció szerint a körfrekvencia a fázis (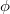
) idő szerinti parciális deriváltja:
![\[\omega '(t) \equiv \frac{{\partial \varphi }}{{\partial t}} = \omega - {\bf{k}} \cdot {\bf{v}}(t)\]](/images/math/0/c/5/0c508082112a0cf5d548c354fcf1fe88.png)
(5)
tehát a két rendszer relatív sebességétől függően a körfrekvencia megváltozik, mégpedig a két vonatkoztatási rendszer relatív sebességének pillanatnyi értéke szerint. (Az egyszerűség kedvéért v és ω időfüggését a továbbiakban nem jelöljük.) Ezt a jelenséget felfedezőjéről Doppler-effektusnak nevezik. A jelenség az akusztikában már XIX században ismert és igazolt volt. (A fenti eredmény csak közelítő jellegű, mivel a Galilei-féle relativitás elvének megfelelő transzformáció, amellyel az egyik koordináta rendszerből áttérünk a másikba, csak a fénysebességhez képest kis v sebességek esetében igaz. A pontos tárgyalásnál a Galilei-féle relativitást fel kell cserélni az Einstein-féle relativitás elvével és ennek megfelelően a két rendszer transzformációját Lorentz-transzformációval kell leírni, ld. a függeléket. A gyakorlatban szinte mindig teljesül az a feltétel, hogy v << c, ahol „c” a fénysebesség, ezért a kapott eredmények nagyon nagy pontossággal érvényben maradnak.) Felhasználva a
![\[{{k = \frac{2\pi }{\lambda }}}\]](/images/math/5/7/5/5755dba41e8a74b0e68a16b11570c88f.png)
egyenleteket, a körfrekvenciáról áttérve frekvenciára kapjuk:
![\[{{f' = f - \frac{\left| {\bf{v}} \right|}{\lambda }\cos \vartheta}}\]](/images/math/3/3/9/3391f86792516d1e242a2e2acb121cfb.png)
(7)
ahol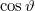 
a k és v vektor által bezárt szög koszinusza. Speciálisan, ha k és v azonos irányú, akkor 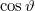, így:
![\[f' = f - \frac{{\left| {\bf{v}} \right|}}{\lambda }\]](/images/math/3/8/7/387114527ec905aa920d3b826b0379dd.png)
(8)
és ha ellentétes irányúak, akkor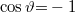 
, melyből:
![\[f' = f + \frac{{\left| {\bf{v}} \right|}}{\lambda }\]](/images/math/d/f/6/df6d04b50a8f2fbf2a3a71bf0b2d5214.png)
(9)
Optikai keverés
Tekintsünk két különböző frekvenciájú (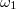
és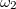 
), és azonos terjedési irányú (x) elektromágneses síkhullámot, ahol az egyik körfrekvencia időfüggő: 
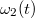. Ebben az esetben az elektromos térerősségek a következőképp írhatók fel:
![\[{E_1} = {E_{10}}\cos \left( {{\omega _1}t - {k_1}x} \right)\]](/images/math/c/9/e/c9ef909735b810f402d07e381615165f.png)
(10)
![\[{E_2} = {E_{20}}\cos \left( {\int\limits_0^t {{\omega _2}(\tau )d\tau } - \int\limits_t^{t - {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}} {{\omega _2}(\tau )d\tau } + \phi } \right) = {E_{20}}\cos \left( {\int\limits_0^{t - {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}} {{\omega _2}(\tau )d\tau + \phi } } \right)\]](/images/math/3/a/4/3a4b219007b094ea241c41909ea3bc61.png)
(11)
ahol „c” a fénysebesség, 
pedig egy konstans fázistolás. Az eredő elektromágneses tér a kettő összege:
![\[E = {E_1} + {E_2} = {E_{10}}\cos \left( {{\omega _1}t - {k_1}x} \right) + {E_{20}}\cos \left( {\int\limits_0^{t - {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}} {{\omega _2}(\tau )d\tau + \phi } } \right)\]](/images/math/8/9/9/899e888fec3b672717ad519f42316b64.png)
(12)
Helyezzünk az eredő tér egy adott pontjába (x) fényérzékelőt. Az érzékelő által szolgáltatott áram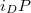 
, ahol „P” a detektorra eső fényteljesítmény. A fényteljesítmény viszont az elektromos térerősség négyzetével arányos:
\[\begin{array}{ccccc}
P{\rm{\~}}{E^2} = & E_{10}^2{\cos ^2}\left( {{\omega _1}t - {k_1}x} \right) +
E_{20}^2{\cos ^2}\left( {\int\limits_0^{t - {\raise0.7ex\hbox{$x$}
\!\mathord{\left/
{\vphantom {x c}}\right.\kern-\nulldelimiterspace}
\!\lower0.7ex\hbox{$c$}}} {{\omega _2}(\tau )d\tau + \phi } } \right) + \\
+ 2{E_{10}}{E_{20}}\cos \left( {{\omega _1}t - {k_1}x} \right)\cos \left(
{\int\limits_0^{t - {\raise0.7ex\hbox{$x$} \!\mathord{\left/
{\vphantom {x c}}\right.\kern-\nulldelimiterspace}
\!\lower0.7ex\hbox{$c$}}} {{\omega _2}(\tau )d\tau + \phi } } \right)\,.
\end{array}\]
Mérési feladatok
