Hőmérsékleti sugárzás vizsgálata
Szerkesztés alatt
A mérés célja:
- a hőmérsékleti sugárzás legfontosabb tulajdonságai-nak és törvényeinek megismerése.
Ennek érdekében:
- összefoglaljuk a hőmérsékleti sugárzásra vonatkozó ismereteket,
- kimérjük egy pontszerű forrás sugárzási intenzitásá-nak távolságfüggését,
- meghatározzuk a fekete test sugárzási intenzitásának hőmérsékletfüggését (Stefan-Boltzmann törvény),
- megvizsgáljuk különböző anyagok abszorpció- és emisszióképességét.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
A tapasztalat szerint két különböző hőmérsékletű test között akkor is végbemegy energiaátadás, ha a hővezetés és a konvektív hőcsere gyakorlatilag elhanyagolható. Az energia ilyenkor elektromágneses sugárzás révén jut át az egyik testről a másikra. Ezt az anyagoknak két alapvető tulajdonsága teszi lehetővé: egyrészt az anyagok külső behatás nélkül - a bennük atomi, molekuláris szinten lezajló mozgások következtében - szünet nélkül, és minden hőmérsékleten elektromágneses sugárzást bocsátanak ki, másrészt az anyagok a rájuk eső elektromágneses sugárzást - ugyancsak atomi, molekuláris mechanizmusok révén - képesek elnyelni. Így egy A test által kibocsátott sugárzásnak egy részét (és az általa szállított energiát) a sugárzás útjába eső B test elnyeli, de ugyanígy, a B test által kibocsátott sugárzás (energia) egy részét az A test nyeli el: szakkifejezéssel élve, az A és B test sugárzási kölcsönhatásban áll egymással. A tapasztalat azt mutatja, hogy az energiacsere eredményeképpen végül is a melegebb testről a hidegebbre megy át energia, tehát a melegebb test hűlni fog, a hidegebb pedig melegedni. Azt azonban, hogy ez a folyamat részleteiben hogyan zajlik le, tehát például adott idő alatt mennyi az átadott energia, csak a sugárzás kibocsátásának illetve elnyelésének részletes tanulmányozásával tudhatjuk meg.
Hőmérsékleti sugárzás és a jellemzésére szolgáló mennyiségek
A testek által külső behatás nélkül kibocsátott elektromágneses sugárzás intenzitását a tapasztalat szerint alapvetően a test hőmérséklete határozza meg, és az intenzitás a test hőmérsékletétől igen erősen függ. A hőmérsékleti sugárzás során létrejött elektromágneses hullámban különböző hullámhosszú összetevők terjednek. A kibocsátott energiának a különböző hullámhosszú összetevők közötti eloszlása - a sugárzás spektrális eloszlása - szintén függ a test hőmérsékletétől. Ezek a tények indokolják azt, hogy az ilyen sugárzást hőmérsékleti sugárzásnak nevezik. A sugárzás kibocsátásának és elnyelésének vizsgálatánál fontos szerepet játszik néhány alapvető fogalom és mennyiség, ezért először ezekkel foglalkozunk.
Egy test által sugárzás útján kibocsátott energiát az emisszió képességgel jellemezzük. Ha a 
hőmérsékletű test egy 
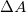nagyságú felületéről 
idő alatt egy 
és 
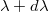közé eső hullámhossztartományban 
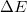energiát sugároz ki, akkor az adott hullámhosszra és hőmérsékletre vonatkozó emisszió képessége:
![\[ \varepsilon (\lambda ,T)= \frac{\Delta E}{\Delta A \Delta t \Delta \lambda}. \]](/images/math/8/9/2/892db9763be064f048ee1a461dc60d04.png)
Ha a kibocsátott energia hullámhossz szerinti (spektrális) eloszlása nem fontos számunkra, akkor a teljes spektrumban kibocsátott, ún. integrált emisszió képességet használhatjuk, amely
![\[ E(T)= \int_0^\infty \varepsilon (\lambda ,T) \, \mathrm{d} \lambda \]](/images/math/b/7/0/b705eaa727019a61b5178d1226d6ab0d.png)
Megjegyezzük, hogy az integrált emisszió képesség értelmezhető a spektrum egyes részeire (pl. infravörös, látható, stb.) is, ilyenkor az integrálás a megfelelő hullámhossztartományra terjed ki.
A már kibocsátott, térben terjedő sugárzás energetikai jellemzésére az energia-áramsűrűséget használjuk. Ez természetesen szintén hullámhosszfüggő mennyiség. Ha a sugárzásban egy és 
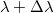közé eső hullámhossztartományban a sugárzás haladási irányára merőleges 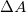nagyságú felületen 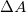idő alatt egy 
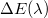energia halad át, akkor az adott hullámhosszra vonatkozó energia-áramsűrűség
![\[ I(\lambda) = \frac{\Delta E(\lambda)}{\Delta A \Delta t \Delta \lambda}. \]](/images/math/4/2/7/427b954c4a38d85ba5666f2200e9eae5.png)
Ezt a mennyiséget a hullámhosszú sugárzás intenzitásának nevezzük. Ha a sugárzásban terjedő összes energiát akarjuk jellemezni, akkor a különböző hullámhoszszakra vonatkozó intenzitások összegzésével kapható teljes intenzitást kell megadnunk:
![\[ I_o = \int_0^\infty I(\lambda) \mathrm{d} \lambda \]](/images/math/8/7/3/873fb7175a1eaa2e287df2ea91449aa8.png)
Az integrált emisszió képességhez hasonlóan, a sugárzási intenzitás is definiálható meghatározott hullámhossz-tartományra .
Ha egy testet sugárzás ér, akkor a testtel való kölcsönhatás következtében a sugárzás (és a szállított energia) több részre bomlik (1. ábra). A sugárzás egy része abszorbeálódik (elnyelődik) a testben. Az intenzitás abszorbeált részének jelölésére az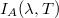 
szimbólumot használjuk. A sugárzás másik része a test felületéről reflektálódik (visszaverődik): 
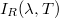, a sugárzás fennmaradó részét pedig a test átereszti: ID (,T). A fenti szimbólumokban a testet érő sugárzás hullámhossza, pedig a sugárzásnak kitett test hőmérséklete, a tapasztalat szerint ugyanis egy test elnyelési-, visszaverési- és áteresztési tulajdonságai általában függnek ezektől a mennyiségektől.
A sugárzásnak a test által elnyelt hányadát, vagyis az
![\[ a(\lambda,T) = \frac{I_A(\lambda,T) }{I(\lambda)} \]](/images/math/b/2/c/b2c83eb483d831d555207298172c0ef8.png)
hányadost a hőmérsékletű test hullámhosszú sugárzásra vonatkozó abszorpció képességének nevezik.
Hasonló módon definiálható a hőmérsékletű test hullámhosszú sugárzásra vonatkozó reflexió képessége
![\[ r(\lambda, T) = \frac{I_R(\lambda,T)}{I(\lambda} \]](/images/math/4/7/5/475a43f25e928461b6d09cc25f67b8b9.png)
![\[ d(\lambda, T) = \frac{I_D(\lambda,T)}{I(\lambda} \]](/images/math/a/e/4/ae4cdd942211071d7cff2973d1b7752c.png)
Ha a testnek csak az összes beérkező sugárzással kapcsolatos viselkedése érdekel bennünket, akkor a fenti hullámhossztól függő (spektrális) jellemzők helyett in-tegrált jellemzőket használunk. A test integrált abszorpció képessége ennek megfelelően
![\[ a(T) = \frac{\int_0^\infty I_A (\lambda,T) \, \mathrm{d} \lambda}{\int_0^\infty I (\lambda) \, \mathrm{d} \lambda} = \frac{I_A(T)}{I} \]](/images/math/7/5/7/7570fcd47c7ba086531318224381513c.png)
Hasonlóan kapható az integrált reflexió képesség
![\[ a(T) = \frac{\int_0^\infty I_R (\lambda,T) \, \mathrm{d} \lambda}{\int_0^\infty I (\lambda) \, \mathrm{d} \lambda} = \frac{I_R(T)}{I} \]](/images/math/a/f/4/af47ff7f759fe413e6386ab73c085f39.png)
és az integrált áteresztő képesség
![\[ a(T) = \frac{\int_0^\infty I_D (\lambda,T) \, \mathrm{d} \lambda}{\int_0^\infty I (\lambda) \, \mathrm{d} \lambda} = \frac{I_D(T)}{I} \]](/images/math/a/1/7/a17bb9ea923e89b35046026fd3675e3f.png)
A fenti jellemzőket - az integrált emisszió képességhez és a sugárzás intenzitásához hasonlóan - szintén lehet de-finiálni egy véges hullámhossztartományra is. Az energia-megmaradás tételéből következik, hogy a fenti jellemzőkre fennállnak az alábbi összefüggések:
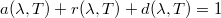, ill
![\[a(T)+r(T)+d(T)=1 \]](/images/math/1/c/7/1c700a124c863f7f3a729ac61ab843d1.png)
A testek sugárzási tulajdonságainak vizsgálatánál igen fontos szerepet játszik az a speciális test, amely a hőmérsékletétől- és a ráeső sugárzás spektrális eloszlásától függetlenül az összes ráeső sugárzást elnyeli. Az ilyen testet abszolút fekete testnek, vagy rövidebben fekete testnek nevezzük, és definíciójának megfelelően, abszorpció képességére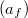 
fennáll, hogy
![\[a_f(\lambda,T)=a_f(T)=a_f=1. \]](/images/math/9/c/0/9c0342e3065d083caa4f4e3fa5895efe.png)
(A fekete testre vonatkozó mennyiségeket 
indexszel jelöljük.)
Jó közelítéssel fekete testnek tekinthető egy üreges test falán lévő kis nyílás (2. ábra), mivel a nyíláson bejutó sugárzásnak az üregből való kijövetele igen kis valószínűségű a nyílás kis mérete miatt. A fekete test jelentős szerepet játszik a sugárzások tanulmányozásánál, mivel a rá vonatkozó törvények elméletileg levezethetőek, és a nem fekete testek esetén is hasznosíthatók.
A fekete test sugárzása
A fekete test által kisugárzott energia elméleti úton meghatározható. Az emisszióképesség hullámhossztól és a test hőmérsékletétől való függésére a kísérleti eredményekkel egyező összefüggést Max Planck vezette le itt nem részletezett meggondolások alapján (ekkor vezette be a foton fogalmát). Az összefüggés egyik gyakran használt alakja a következő:
![\[ \varepsilon_f(\lambda,T)=\frac{c_1\lambda^{-5} }{exp \left(\frac{c_2}{\lambda T} \right) -1}. \]](/images/math/d/7/6/d76f83e9f27cbe66a29f39858c56e678.png)
Ez a Planck-féle sugárzási törvény (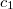
és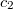 
állandók). Az emisszióképesség hullámhosszfüggése néhány hőmérsékleten a 3. ábrán látható. Adott hőmérsékleten a fekete test emisszióképessége maximumot mutat. A maximumnak megfelelő hullámhossz növekvő hőmérséklettel csökken.
Az ábrán feltüntetett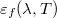 
mennyiség a fekete test által az egységnyi hullámhossz intervallumban (egységnyi felületről) kisugárzott teljesítményt adja meg. Ennek megfelelően a 
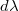intervallumhoz tartozó teljesítmény
![\[ \mathrm{d}E_f=\varepsilon_f (\lambda,T)\mathrm{d}\lambda =\frac{c_1\lambda^{-5} }{exp \left(\frac{c_2}{\lambda T} \right) -1} \mathrm{d}\lambda \]](/images/math/2/c/d/2cd54392813ceaf93911aa3f1798f989.png)
Könnyen belátható, hogy ennek számértékét az ábrán a bevonalkázott terület adja meg. A hőmérsékletű fekete test egységnyi felületéről a teljes spektrumban kisugárzott teljesítmény (14) integrálásával kapható meg:
![\[ E_f (T)=\int_0^\infty \frac{c_1\lambda^{-5} }{exp \left(\frac{c_2}{\lambda T} \right) -1} \mathrm{d}\lambda \]](/images/math/a/8/d/a8dd94487aee01806c8a3acaa231f3d6.png)
Az integrálás eredménye a következő:
![\[ E_f(T)=\sigma T^4 \]](/images/math/3/4/0/3401029f00dd965ba5614d803f5630a1.png)
Ez a Stefan-Boltzmann törvény, mely szerint a T hőmérsékletű fekete test egységnyi felülete által egységnyi idő alatt kisugárzott teljes energia arányos a test hőmérsékletének negyedik hatványával. A törvényben szereplő 
állandó értéke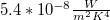 
.
A Stefan-Boltzmann törvény a fekete test által minden irányban kisugárzott összteljesítményt adja meg. A tapasztalat szerint azonban egy felületről ugyanolyan térszögbe kisugárzott energia függ a felülethez viszonyított iránytól. A sugárzás intenzitásának irányfüggését fekete test esetén a Lambert-törvény adja meg, amely szerint egységnyi felület által a felület n normálisával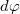 
szöget bezáró irányban a 
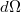térszögben egységnyi idő alatt kisugárzott energia (4. ábra):
![\[ \mathrm{d}E_\varphi (T) =\frac{\sigma}{\pi}T^4 \mathrm{d} \Omega cos\varphi \]](/images/math/4/0/9/4093864552a10e55ddf543ed0d4a2a23.png)
