Elektron fajlagos töltésének (e/m) mérése. Franck-Hertz kísérlet.
Tartalomjegyzék |
Elektron fajlagos töltésének (e/M) mérése
A mérés célja:
- elektromos- és mágneses térben mozgó töltött részecske viselkedésének megismerése
- az elektron fajlagos töltésének meghatározása.
Ennek érdekében :
- összefoglaljuk az elektromos- és mágneses térben mozgó töltött részecskére ható erők alaptörvényeit és az alkalmazott e/m mérési módszerek elvi alapjait,
- két független mérési módszerrel megmérjük az elektron fajlagos töltését.
Elméleti összefoglaló
Az általunk ismert anyag egyik alapvető építőköve az elektron, ezért legfontosabb adatainak ismerete az anyag tulajdonságainak mélyebb megértéséhez nélkülözhetetlen. Az elektron töltése (e) viszonylag egyszerű módszerrel meghatározható (először Millikan mérte meg ), tömegét (m) azonban közvetlenül nem tudjuk meghatározni. Megmérhető azonban töltésének és tömegének hányadosa (e/m), az úgynevezett fajlagos töltés, amelyből a töltés ismeretében a tömeg meghatározható.
A fajlagos töltés mérésének általunk használt módszerei azon alapulnak, hogy mágneses térben mozgó töltésre erő hat, amely eltéríti azt eredeti pályájától, és az eltérítés mértéke a fajlagos töltéstől függ. A mérés során speciális eltérítést valósítunk meg: a mágneses térben mozgó töltések a rájuk ható mágneses eltérítő erő hatására körpályán mozognak. A fajlagos töltés meghatározása lényegében a létrejött körpálya sugarának közvetlen vagy közvetett úton történő mérése alapján történik.
Egy  térerősségű elektromos- és
térerősségű elektromos- és  mágneses indukciójú mágneses térben sebességgel mozgó e töltésre ható úgynevezett Lorentz-erő:
mágneses indukciójú mágneses térben sebességgel mozgó e töltésre ható úgynevezett Lorentz-erő:
![\[ F_L = e(E+v\times B) \]](/images/math/c/1/e/c1e0f760c7b3286e9e0c8a6027224c4e.png)
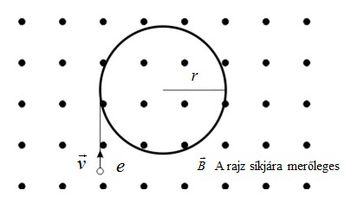
A mozgó töltés a pályáján az elektromos tér hatására a térerősséggel párhuzamos egyenes mentén térül el, míg a mágneses tér a sebességre és a mágneses térre merőleges eltérülést okoz. Könnyen belátható, hogy ha csak mágneses tér van jelen és a töltés a mágneses térre merőlegesen mozog, akkor az eltérítő erő, – amely mindig merőleges a sebességre – a részecskét körpályára kényszeríti. (1.ábra)
Mivel a részecskét körpályán tartó centripetális erő nagysága ekkor az
![\[ F_m = evB \]](/images/math/4/4/5/44518140638b85a2cd2941601509ee1b.png)
mágneses erő, a részecske mozfásegyenlete:
![\[ evB = m\frac{v^{2} }{r}. \]](/images/math/b/1/5/b15d7bc380146331cafa0e72cd6b2d78.png)
Ebből (a körpálya sugara helyett annak átmérőjét, d-t használva) a fajlagos töltésre az alábbi kifejezést kapjuk:
![\[ \frac{e}{m} =\frac{2v}{Bd} \]](/images/math/7/7/9/7798e4798bbe75969ac92bb8fd9e9f82.png)
Ha tehát az elektron sebességét, a pálya átmérőjét és a mágneses indukcióvektor nagyságát ismerjük, akkor a fenti egyenletből a fajlagos töltés kiszámítható. A számításhoz szükséges adatokat az alábbi módon határozhatjuk meg.
Az elektronokat homogén elektromos térrel gyorsítjuk fel, így sebességük a munkatételből kiszámítható. (Az elektronok kezdősebessége elhanyagolható a gyorsítással megszerzett sebességhez képest.)
![\[ eU_gy = \frac{1}{2}mv^{2} \]](/images/math/7/4/c/74cd666376f493ae3868059a71e49876.png)
![\[ v = \sqrt{\frac{2eU_{gy} }{m} } \]](/images/math/8/2/2/8222e48420ff507531b2b48e222378ef.png)
Itt 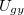 az elektronokat gyorsító feszültség, melyet a mérés során magunk állíthatunk be és mérhetünk meg.
az elektronokat gyorsító feszültség, melyet a mérés során magunk állíthatunk be és mérhetünk meg.
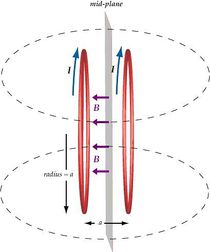
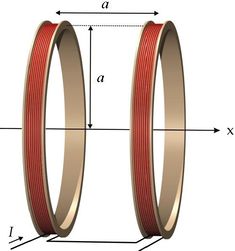
A mágneses teret az egyik mérési elrendezésnél két rövid tekerccsel (sokmenetű hurokkal) állítjuk elő, amelyeket közös tengely mentén úgy helyezünk el, hogy meneteik egymással párhuzamosan állnak és a tekercsek sugara megegyezik a távolságukkal.
Kimutatható (lásd Simonyi: Elméleti villamosságtan, Tankönyvkiadó), hogy ez az úgynevezett Helmoltz-féle elrendezés (Helmholtz-tekercs) a tekercsek közötti térrészben homogén mágneses teret hoz létre, melyben a mágneses indukcióvektor nagysága:
![\[ B=\frac{\mu_0 I_m N}{\left(\frac{5}{4}\right)^{\frac{3}{2} } a} , \]](/images/math/a/f/8/af88a6cbbfbbb06d274b2a57bac4b7b5.png)
ahol  a tekercsek menetszáma, a azok egymástól mért távolsága,
a tekercsek menetszáma, a azok egymástól mért távolsága, 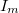 a mágneses teret létrehozó áram erőssége,
a mágneses teret létrehozó áram erőssége, 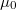 pedig a vákuum permeabilitása:
pedig a vákuum permeabilitása: 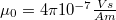 .
A második mérési módszernél a mágneses teret hosszú egyenes tekerccsel állítjuk elő, ekkor a mágneses indukcióvektor nagysága az ismert
.
A második mérési módszernél a mágneses teret hosszú egyenes tekerccsel állítjuk elő, ekkor a mágneses indukcióvektor nagysága az ismert
![\[ B=\frac{\mu_0 I_m N}{l} \]](/images/math/f/6/5/f6598bce8fd0af94db53dbe10c01d4e3.png)
összefüggésből kapható, amelyben  a tekercs menetszáma,
a tekercs menetszáma,  a hossza és $I_m a mágnesező áram erőssége.
a hossza és $I_m a mágnesező áram erőssége.
Az e/m arány mérése
e-m mérés a körpálya közvetlen megfigyelése alapján
Az elektron fajlagos töltésének meghatározására szolgáló egyik eljárás a körpályán mozgó elektronok - és a körpálya – közvetlen megfigyelésén alapul. Az ehhez használt berendezésben az eltérítő mágneses teret Helmholtz-tekerccsel hozzuk létre és egy speciális gáztöltésű üvegedényben láthatóvá válik a pálya, amelyen az elektronok mozognak. Ebben az esetben tehát a körpálya d átmérője közvetlenül megmérhető és az e/m értéke (4), (6), és (7) alapján további mérhető vagy ismert értékek segítségével kiszámítható:
![\[ \frac{e}{m} = \frac{8 \left(\frac{5}{4}\right)^{3} a^{2} U_{gy} }{(\mu_0 NdI_m)^{2} } \]](/images/math/e/f/e/efe851d797694698f228e0e3cf62e9ab.png)
Annak érdekében, hogy a fajlagos töltés értékét elegendő pontossággal kapjuk meg, több mérést célszerű végezni. (9) jobb oldalán álló kifejezés két paraméterét tudjuk változtatni. A pálya átmérője adott mágnesező áram mellett az alábbi szerint függ a gyorsító feszültségtől:
![\[ d=\frac{8^{\frac{1}{2} } \left(\frac{5}{4}\right)^{\frac{3}{2} } a }{\mu_0N\left(\frac{e}{m}\right)^{\frac{1}{2} } I_m } \sqrt{U_{gy} } \]](/images/math/5/1/f/51f000e49b5ab72442008930956fc0f6.png)
Ha tehát megmérjük a pálya átmérőjét néhány gyorsító feszültség értéknél és megrajzoljuk a 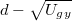 grafikont, akkor a kapott egyenes meredeksége (
grafikont, akkor a kapott egyenes meredeksége (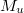 ) többek között az e/m hányadossal arányos, vagyis:
) többek között az e/m hányadossal arányos, vagyis:
![\[ \frac{e}{m} = \frac{8 \left(\frac{5}{4}\right)^{3} a^{2} }{\mu_0^{2}N^{2}I_m^{2}M_U^{2} } \]](/images/math/b/7/e/b7ef83b33f4dc02cf215d8df7ab84806.png)
Állandó gyorsító feszültség mellett az elektronok pályasugara a mágnesező áramtól az alábbi szerint változik:
![\[ d= \frac{8^{\frac{1}{2} } \left(\frac{5}{4}\right)^{\frac{3}{2} } aU_{gy}^{\frac{1}{2} } }{\mu_0N\left(\frac{e}{m}\right)^{\frac{1}{2} } } \frac{1}{I_m} \]](/images/math/3/1/6/316c80300dcfca4c8a7d9c0fbb34953b.png)
Most a különböző mágnesező áramok mellett kapott pályaátmérőket az 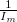 függvényében ábrázolva a grafikon
függvényében ábrázolva a grafikon 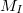 meredekségével fejezhető ki az
meredekségével fejezhető ki az 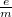 hányados:
hányados:
![\[ \frac{e}{m} = \frac{8\left(\frac{5}{4}\right)^{3}a^{2}U_{gy} }{\mu_0^{2}N^{2}M_I^{2} } \]](/images/math/c/4/1/c4105dfdeaa275b8bd1992b87530e285.png)
e/m mérése a körpálya közvetett vizsgálata alapján
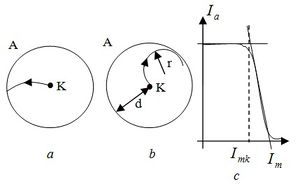
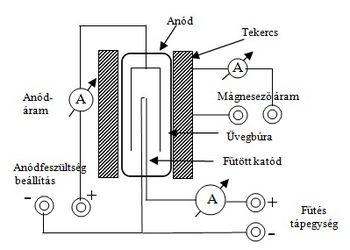
Az itt használt második mérőberendezésben a mágneses térben mozgó elektronok pályájáról közvetett úton szerzünk információt. Ehhez egy olyan elektroncsövet használunk, amelyben az elektronokat kibocsátó katódot egy hengeres anódlemez veszi körül és a katóddal valamint a henger tengelyével párhuzamos mágneses térbe helyezzük. (9. ábra) Az anódra adott pozitív feszültség hatására a fűtött katódról az elektronok az anód felé mozognak, ezért az elektroncsövön áram (úgynevezett anódáram) folyik. Ha mágneses teret hozunk létre, akkor az elektronok eltérülnek a katódból (K) kiinduló sugárirányú pályájuktól és kis mágneses tér esetén az anódot (A) görbült pályán érik el. (2.a ábra)
A mágneses teret növelve elérünk egy olyan kritikus értéket, amelynél az elektronok zárt pályán mozognak és nem érik el az anódot 2.b ábra) Ekkor az elektroncsőben folyó áram megszűnik.
Ha ismerjük a kritikus mágneses teret, az elektronokat gyorsító feszültséget (ezáltal azok sebességét is) és a katód-anód távolságot (ami itt az elektronpálya átmérője lesz), akkor a fajlagos töltés – hasonlóan az előző módszerhez – a (4) alapján számítható.
Most tehát a mérés során állandó elektronpálya –átmérővel dolgozunk, és az elektroncsövön átfolyó áramot mérve megkeressük azt a mágnesező áramot (mágneses teret), amelynél a pályasugár éppen a cső szerkezetéből adódó érték.
A mágneses teret ebben az elrendezésben egy hosszú egyenes tekerccsel állítjuk elő , így a mágneses indukcióvektor nagysága ( ) a tekercsben folyó
) a tekercsben folyó 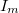 mágnesező áram ismeretében a (8) egyenletből kapható meg.
mágnesező áram ismeretében a (8) egyenletből kapható meg.
Az elektronok sebességének meghatározása az előző méréshez képest most egy kicsit bonyolultabb. A probléma az, hogy az elektronok gyorsítása most az anód és katód közötti térben zajlik, ahol a potenciál értéke az izzó katódtól az anód felé haladva fokozatosan nő, tehát az elektronok sugárirányú sebessége csak fokozatosan éri el a (6) egyenletnek megfelelő értéket. Ennek következtében a mágneses térben mozgó elektronok sebessége a mozgás folyamán változik, így egyrészt az elektronok valódi pályája nem lesz pontosan kör alakú, másrészt az anódáram nem hirtelen, egy jól meghatározott mágneses indukciónál tűnik el, hanem a térerősség növelése során fokozatosan csökken. (2.c ábra)
Részletes számítások szerint a „körpálya” modell megtartható, ha a valódi 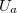 anódfeszültség helyett egy „effektív” feszültséget definiálunk az alábbi egyenlettel:
anódfeszültség helyett egy „effektív” feszültséget definiálunk az alábbi egyenlettel:
![\[ U_{eff} = \frac{3}{2}U_a \]](/images/math/a/c/0/ac0a1ae5c72f2531283afb9dfe2794f5.png)
A jelenség elemzése azt is megmutatja, hogy a fokozatosan csökkenő anódáramból hogyan lehet a kritikus mágneses teret meghatározni: eszerint a kritikus mágneses tér az anódáram csökkenésének kezdetéhez rendelhető hozzá. Ennek megfelelően az anódáram-mágnesező áram grafikon alapján a 2.c ábrán látható módon meghatározzuk a kritikus mágnesező áramot (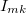 ), majd ebből (8) segítségével a kritikus mágneses indukciót.
), majd ebből (8) segítségével a kritikus mágneses indukciót.
Az effektív feszültség felhasználásával az elektronok „effektív” sebessége a (6) és (14) egyenletekkel így alakul.
![\[ v=\sqrt{\frac{3eU_a}{m} } \]](/images/math/8/2/1/8218a832bbed0d58c1e4b4ac0809c330.png)
A kritikus mágneses térnek megfelelő mágnesező áram (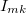 ) esetén az effektív körpálya sugara:
) esetén az effektív körpálya sugara:
![\[ r=\frac{d}{2} \]](/images/math/0/d/b/0db0916dd428a54235ad46f0a955d59b.png)
ahol a katód-anód távolság. (2.b ábra) A fentiek alapján a (4), (15), (8) és (16) összefüggések segítségével az elektron fajlagos töltésére az alábbi kifejezést kapjuk:
![\[ \frac{e}{m} = \frac{12l^{2}U_a}{\mu_0^{2}N^{2}i_{mk}^{2}d^{2} } \]](/images/math/d/2/0/d20f93de593fe165b90da2fb1a00d32e.png)
Ismernünk kell tehát a mágneses teret előállító tekercs adatait (hosszát, menetszámát), az elektroncső anód-katód távolságát, az anódfeszültséget és a kritikus mágnesező áramot.
A mérőberendezések és használatuk
e/m mérés a körpálya közvetlen megfigyelése alapján
Az ehhez a méréshez használt speciális mérőberendezés vázlata a 3. és 4. ábrán található.
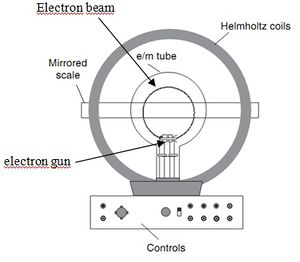
Az elektronok pályáját egy kisnyomású héliummal töltött üvegedényben figyeljük meg, ami lényegében egy speciális katódsugárcső. A csőben a nagysebességű elektronokat egy elektronágyú hozza létre, amelyben egy izzó katód elektronokat kelt majd ezeket egy kívülről szabályozható gyorsító feszültség felgyorsítja.
A felgyorsított elektronok egy része útja során a He atomokat gerjeszti, amelyek az alapállapotba való visszatérésük során látható tartományú fényt bocsátanak ki, és így kirajzolják az elektronok pályáját. A mágneses teret a katódsugárcsövet közrefogó Helmholtz-tekercsek hozzák létre, amelynek a méréséhez szükséges elektronikát tartalmazó dobozra vannak felszerelve. Maga a cső szintén ezen a dobozon helyezkedik el, de foglalata függőleges tengely körül forgatható, így az elektronok körpályájának síkja a tekercsekkel párhuzamosan , vagyis a mágneses térre merőlegesen beállítható.
A méréshez hozzátartozik egy sötétítő sapka, amelynek alkalmazásával a mérés nappali fénynél is elvégezhető. Az elektronpálya átmérőjének meghatározásához egy tükröző, megvilágított skála szolgál. A tükör azért szükséges, hogy a körpálya szélső pontjának helyét úgy tudjuk leolvasni, hogy a szemünket a pálya szélső pontjával összekötő egyenes merőleges legyen a skálára. (Így elkerülhető a parallaxis-hiba.)
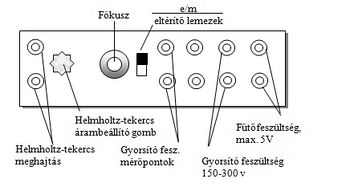
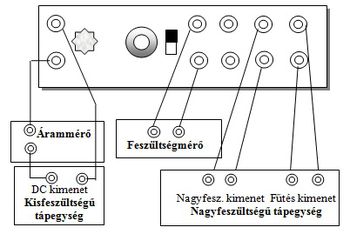
Az elektronikát tartalmazó doboz (továbbiakban mérőegység) előlapján találjuk az elektromos csatlakozó hüvelyeket és a kezelőszerveket. (5. ábra)
A jobb oldali csatlakozópár a katód fűtőáramának bevezetésére (max. 6,3 V) , balra haladva a következő pár a gyorsító feszültség (max. 300 V) csatlakoztatására szolgál, a harmadik csatlakozópár pedig az elektronsugár elektromos eltérítését lehetővé tevő feszültséget csatlakoztat a csőben levő két elektródra (a mérés során ezeket nem használjuk). A jobbról negyedik csatlakozópáron mérhetjük a gyorsító feszültséget. Ezután balra tovább haladva egy kapcsoló következik, amivel az elektromos és mágneses eltérítési mód alkalmazása között választhatunk (most a mágneses eltérítést választjuk, a kapcsoló a felső, e/m jelű állásban legyen). Az elektronsugarat a kapcsoló melletti focus forgatógombbal fókuszálhatjuk. Az előlap bal oldalán találjuk a Helmholtz-tekercset meghajtó áram csatlakozóját, mellette jobbra van az áram nagyságát szabályozó potenciométer forgatógombja. A méréshez szükséges áramokat és feszültségeket két tápegység biztosítja.
A kisfeszültségű tápegység (Low Voltage Power Supply, 6. ábra) szolgáltatja a Helmholtz-tekercs mágnesező áramát, amelyet a baloldali kimenetpárról (0-21 Volts DC) egy árammérőn keresztül vezetünk a mérőegység megfelelő csatlakozópárjához. A tápegységen található egy mutatós műszer, amely a Meter Select nyomógomb benyomott állapotában a baloldali kimenetpárból kifolyó áramot, kiengedett állapotában pedig az ott beállított feszültséget méri.
Ezzel a műszerrel a mérésnél feszültséget mérjünk, a tekercs áramát pedig külön műszerrel. A DC Voltage Adjust potenciométerrel állítsunk be 8 V-ot. Ha ez nem lehetséges, akkor a DC Current Adjust gombot forgassuk jobbra mindaddig, amíg a 8 V beállíthatóvá válik.
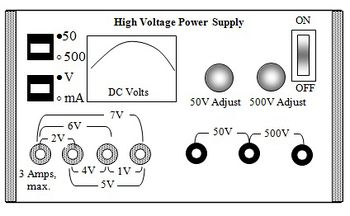
A nagyfeszültségű tápegységet (High Voltage Power Supply, 7. ábra) a mérés során az elektronágyú működtetésére használjuk.
A katód fűtésére a bal oldali váltóáramú kimenetek közül az 5 V-tal jelölt kimenetpárt használjuk, az elektronokat gyorsító feszültséget pedig a jobb oldali, nagyfeszültségű, 500 V jelzésű kimenet-párról csatlakoztassuk a mérőegység megfelelő csatlakozó-párjára. A kimeneten megjelenő feszültség az 500 V Adjust potenciométerrel szabályozható. A műszer bekapcsolása előtt ezt a gombot csavarjuk teljesen balra! A tápegységen található mutatós műszer az itt beállított feszültséget mutatja, de ennek pontos értékét külön műszerrel mérjük meg.
A mérőberendezés, a tápegységek és a mérőműszerek csatlakoztatás a 8. ábra mutatja.
A mérés menete
- Állítsuk össze a 8. ábrán szereplő kapcsolást és bekapcsolás előtt ellenőriztessük a gyakorlatvezetővel.
- Tegyük fel a berendezésre a sötétítő sapkát.
- Kapcsoljuk a mérőegységet az e/m Measure állásba.
- A mérőegység előlapján a Helmholtz-tekercsek áramszabályozóját (Current Adjust Knob) és a fókuszáló gombot (Focus) tekerjük teljesen balra (ekkor a tekercs árama nulla, az elektronsugár pedig fókuszálatlan, intenzitása maximális).
- A tápegységeken állítsuk be a következő értékeket:
Nagyfeszültségű tápegység nagyfeszültségű kimenetén 150V, az elektronágyú katódjának fűtése az 5V-hoz csatlakozik. Kisfeszültségű tápegység egyenáramú kimenetét (Helmholtz-tekercsek árama) állítsuk 8 V-ra (ezt a tápegység műszerével mérjük), és az áramszabályzó gomb jobbra forgatásával állítsunk be 1,5 A mágnesező áramot.
- Néhány percen belül bemelegszik az elektronágyú és megjelenik az elektronsugár. A mágnesező áram finom állításával elérhető, hogy a pálya a gömböt kitöltő kör alakú legyen. A fókusz gombbal állítsunk elő vékony, de jól látható nyalábot. A cső óvatos forgatásával az esetlegesen spirál alakú pályát síkba kell állítani
- A pálya átmérőjét az alábbiak szerint olvassuk le:
Illesszük a mérőegység doboza elé a mérőhelyen található optikai sínt. Ezen egy lovas van, amelyre egy vékony fémlap csatlakozik függőlegesen. Ennek a lapnak a síkja merőleges az elektronok pályájára és a gömb mögötti tükörskálára. A lovas csúsztatásával beállítható, hogy a fémlap, a körpálya széle és a fémlap tükörképe egy egyenesbe essen. A lovas helyzetét az optikai sínen levő skáláról lehet leolvasni.
- A fajlagos töltés meghatározásához szükséges további adatok a következők:
- A Helmholtz-tekercsek menetszáma: N=130
- A tekercsek távolsága: a=15cm
e/m mérés a körpálya közvetett megfigyelése alapján
A mérőberendezés kialakítását a 9. ábra mutatja
A mérődoboz 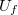 banánhüvely párjához árammérőn keresztül csatlakoztassuk egy Hameg tápegység 5 V-os kimenetét. Az anódfeszültséget ennek a tápegységnek a 0-20 V-os kimenetéről vegyük, az anódáramot multiméterrel mérjük. (A fűtőfeszültség és anódfeszültség negatív pólusai legyenek közösek.) A mágnesező áramot a Hameg tápegység másik 0-20 V-os kimenetéről vegyük, ennek értékét is árammérővel mérjük.
banánhüvely párjához árammérőn keresztül csatlakoztassuk egy Hameg tápegység 5 V-os kimenetét. Az anódfeszültséget ennek a tápegységnek a 0-20 V-os kimenetéről vegyük, az anódáramot multiméterrel mérjük. (A fűtőfeszültség és anódfeszültség negatív pólusai legyenek közösek.) A mágnesező áramot a Hameg tápegység másik 0-20 V-os kimenetéről vegyük, ennek értékét is árammérővel mérjük.
Mérési feladat
- Állítsunk be 20 V anód-feszültséget
- A mágnesező áramot 10mA-es lépésekben növelve 520 mA-ig olvassuk le az anódáram értékét.
- A mágnesező-áram - anód-áram függvényt ábrázolva állapítsuk meg az kritikus áramértéket(lásd 2/c ábra), számoljuk ki az $I_{mk} hányadost és vessük össze az irodalmi adatokból származó értékkel!
- A mérési összeállítás szükséges adatai:
- a tekercs menetszáma: N=1600
- a tekercs hossza: l=5cm
- Anód-katód távolság ( a körpálya átmérője): d=3mm
- Végezze el a mérést 17V és 14V anódfeszültséggel is.
- A három
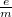 értékből számoljon átlagot.
értékből számoljon átlagot.
Fontos balesetvédelmi tudnivalók
Nagyfeszültség alkalmazásánál fokozott óvatossággal járjunk el!
- soha ne dolgozzunk egyedül
- dolgozzunk egy kézzel, a másik kezünket dugjuk zsebre, vagy tartsuk a hátunk mögött
- Itt fokozottan érvényes az az általános szabály, hogy a csatlakozó zsinórok dugaszolását vagy a csatlakozások megváltoztatását KIZÁRÓLAG feszültségmentes állapotban végezzük!
Franck-Hertz kísérlet
Elméleti összefoglaló
Az atomfizikában a Planck-féle hatáskvantum, a Planck-állandó bevezetésével a korábbi klasszikus fizikai felfogással teljesen ellentétes új felismerés terjedt el: atomi méretekben az energiaátadás már nem folytonosan, hanem diszkrét mennyiségekben, úgynevezett kvantumokban következik be. Ennek a felismerésnek egyik közvetlen bizonyítékát Franck és Hertz elektronütközési kísérletei szolgáltatták.
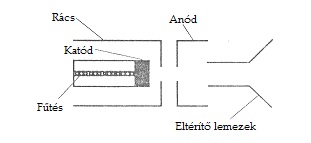
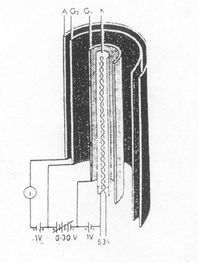
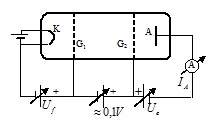
A kísérlethez használt cső (1. ábra) egy kisnyomású higanygőzt tartalmazó, egyébként a vákuum-triódához hasonló cső, amelynél az egyenes K izzókatód elektron emisszióját egy ehhez közeli koaxiális G1 rács szabályozza. A katódból kilépő elektronokat egy további, változtatható (0 – 30 V) feszültségű, szintén koaxiális G2 rács gyorsítja. A G2 rácson áthaladó, egy minimális energiával rendelkező elektronokat egy csekély (0,5 – 1,5 V) negatív feszültségű A gyűjtő elektróda fogja fel. A cső egy csepp higanyt tartalmaz, mely mintegy 200 oC hőmérsékleten kb. 15 Hgmm gőznyomást eredményez és hatására az elektronok a katódtól a gyűjtő elektródig tartó útjuk során gyakran ütköznek Hg atomokkal. Az ütközések általában rugalmasak és a gyorsító feszültséget fokozatosan növelve az áram eleinte nő, mint a vákuum triódáknál. Az ilyen ütközések során az elektronok a hozzájuk képest nagy tömegű Hg atomokon nem vesztenek energiát, tehát az elektronok túlnyomó többsége képes a G2 rács és az anód közötti gyenge ellentéren áthaladni. Amikor az elektronok kinetikus energiája eléri a Hg atomok 4,9 eV-os első gerjesztési energiáját, az ütközések rugalmatlanná válnak, az elektronok túlnyomó része a Hg atomokkal való ütközés során átadja energiáját azoknak és nem képesek áthatolni az említett gyenge ellentéren sem. Ezért az áram hirtelen lecsökken.
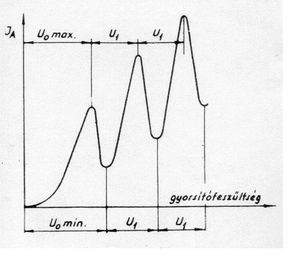
A gyorsító feszültséget tovább növelve az áram ismét nő jelezve azt, hogy az elektronok a G2 anódrácsig újra felgyorsulnak és átjutnak az A elektródra. További gyorsító feszültség növeléskor az elektronok többször képesek felgyorsulni a rugalmatlan ütközést eredményező energiára, ezért az áram-feszültség görbében közelítőleg egyenlő távolságokra jellegzetes minimumok és maximumok figyelhetők meg (2. ábra). Franck és Hertz azt tapasztalták, hogy a higanygőz 4,9 V gyorsító feszültségnél 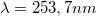 hullámhosszú fényt bocsát ki, amelynek
hullámhosszú fényt bocsát ki, amelynek 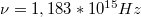 frekvenciája megegyezik azon foton ener-giájával, amely a Hg atom első gerjesztett állapotából az alapállapotba történő spontán visszatérésekor emittál. Eszerint, két maximum közötti
frekvenciája megegyezik azon foton ener-giájával, amely a Hg atom első gerjesztett állapotából az alapállapotba történő spontán visszatérésekor emittál. Eszerint, két maximum közötti 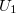 potenciálkülönbség az első gerjesztési potenciál. Az
potenciálkülönbség az első gerjesztési potenciál. Az 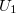 gerjesztési potenciál meghatározásához lemérjük az anódáram-gyorsító feszültség görbe maximumainak távolságait. A kapott mérési eredmények számtani közepét képezve megkapjuk
gerjesztési potenciál meghatározásához lemérjük az anódáram-gyorsító feszültség görbe maximumainak távolságait. A kapott mérési eredmények számtani közepét képezve megkapjuk 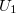 közelítő értékét.
közelítő értékét.
A magasabb gerjesztett állapotok kimutatására Franck és Hertz a kapcsolási elrendezést a következőképpen módosí-tották (3. ábra): a katódból kilépő elektronok a katód és az ahhoz igen közeli G1 gyorsít rács közötti feszültség hatásá-ra gyorsulnak. Mivel ezen a rövid szakaszon a kisnyomású higanygőzben a rugalmatlan ütközések ritkák, viszonylag sok elektron a gyorsító feszültségnek megfelelő energiával kerül a G1 gyorsító rács és a G2 anódrács közötti hosszú, gyakorlatilag erőmentes térrészbe. G2 és az anód megfelelő energiájú elektronok a G1 és a G2 rács között elvesztették energiáikat. A G2 és az A elektródok között most is csekély ellentér van. Az áram- feszültség karakterisztikán mutatkozó jól észrevehető esések vagy törések jelzik, hogy a Hg magasabb rendű gerjesztési potenciáljainak megfelelő energiájú elektronok a G1 és G2 rácsok között elvesztették energiájukat.
Franck-Hertz kísérlet neon gázzal töltött kisülési csővel
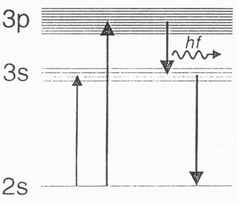
A Neon gáznál a gerjesztés illetve rekombináció folyamata a higany atoménál komplikáltabb. A rugalmatlan elektronütközéses gerjesztés a legvalószínűbb úton az alapállapot és a 10 db 3p gerjesztett állapot között történhet, amelyek energiái 18,4 eV és 19,0 eV közé esnek. A négy alacsonyabb energiájú 3s állapot energiái a 16,6 eV és 16,9 eV értékek között vannak. A magasabb 3p állapotból az alapállapotba történő legerjesztődés mindig a 3s energiasávon keresztül történik.. Eközben a 3p és 3s sávok közötti átmenetnél látható fény tartományába eső foton kibocsátása észlelhető. A folyamatot a 4. ábra mutatja be.
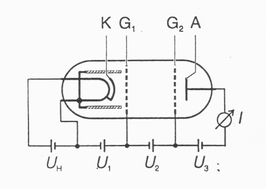
A Ne kisülési cső szobahőmérsékleten működik és a gáz töltet nyomása kb. 10 hPa. A kisülési cső elektródáinak sematikus elrendezését az 5. ábra mutatja be.
A csőben négy elektród található, melyek jelölései:
- K : katód (melyet közvetetten fűtünk
 = 6,3 V feszültséggel )
= 6,3 V feszültséggel )
- G1 : vezérlőrács (a katód és G1 közé kapcsolt feszültség
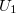 )
)
- G2 : gyorsító rács ( a G1 és G2 rácsok közé kapcsolt feszültség
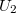 )
)
- A : anód ( a G2 és A közé kapcsolt feszültség
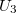 )
)
A fűtött katódból emittált elektronok elektronfelhőt képeznek, melyet 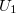 potenciál segítségével a G1 rácsig vezetünk. Az emissziós áram gyakorlatilag független az
potenciál segítségével a G1 rácsig vezetünk. Az emissziós áram gyakorlatilag független az 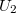 (rácsok közötti) potenciáltól, ha elhanyagoljuk a visszaszóródott elektronok hatását. Az
(rácsok közötti) potenciáltól, ha elhanyagoljuk a visszaszóródott elektronok hatását. Az 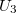 fékező feszültség segítségével csak azon elektronok jutnak az anódra, melyek kinetikus energiája a fékező térrel szemben elegendően nagy. Ezen elektronok árama az
fékező feszültség segítségével csak azon elektronok jutnak az anódra, melyek kinetikus energiája a fékező térrel szemben elegendően nagy. Ezen elektronok árama az 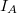 kollektoráram.
kollektoráram.
A kísérletben az 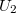 gyorsító feszültséget változtatjuk 0 ...60 V között, miközben
gyorsító feszültséget változtatjuk 0 ...60 V között, miközben 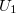 és
és 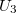 feszültségeket állandó értéken tartva az
feszültségeket állandó értéken tartva az 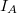 anódáramot mérjük. A mérés során az áram kezdetben nő (a konvencionális tetródákhoz hasonlóan), és akkor ér el maximumot, ha a G2 rács közelében az elektronok kinetikus energiája elegendően nagy ahhoz, hogy ütközéssel gerjessze a Ne atomokat. Ekkor az anódáram hirtelen lecsökken, mivel az ütközés utáni elektronok lecsökkent kinetikus energiája nem elég az
anódáramot mérjük. A mérés során az áram kezdetben nő (a konvencionális tetródákhoz hasonlóan), és akkor ér el maximumot, ha a G2 rács közelében az elektronok kinetikus energiája elegendően nagy ahhoz, hogy ütközéssel gerjessze a Ne atomokat. Ekkor az anódáram hirtelen lecsökken, mivel az ütközés utáni elektronok lecsökkent kinetikus energiája nem elég az 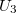 fékező potenciálon történő áthaladáshoz. Ahogy az
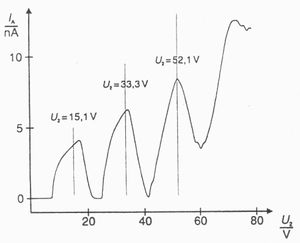
fékező potenciálon történő áthaladáshoz. Ahogy az 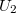 gyorsító feszültség tovább nő, úgy a Ne atomok gerjesztésének megfelelő kinetikus energiájú elektronok egyre beljebb kerülnek a rácsok közötti tartományba, eltávolodva a G2 rácstól. A Ne atomokkal történt ütközés után az elektronok újra gyorsulnak és elegendően nagy feszültségnél ismét a gerjesztéséhez szükséges energiát abszorbeálva atomokat gerjeszthetnek.( 6. ábra)
gyorsító feszültség tovább nő, úgy a Ne atomok gerjesztésének megfelelő kinetikus energiájú elektronok egyre beljebb kerülnek a rácsok közötti tartományba, eltávolodva a G2 rácstól. A Ne atomokkal történt ütközés után az elektronok újra gyorsulnak és elegendően nagy feszültségnél ismét a gerjesztéséhez szükséges energiát abszorbeálva atomokat gerjeszthetnek.( 6. ábra)
Ez eredményezi a kollektor áram második maximum-minimumát. Magas gyorsító feszültség esetén a G1 és G2 rácsok közötti térben diszkrét vörös lumineszkáló rétegek figyelhetőek meg.
Mérőegység beállítása számítógépes adatgyűj-tés esetén, programozható tápegységgel.
A Hameg hármas tápegységen állítsa be az alábbi feszültségeket:
- Fűtőfeszültség: 5V.
- Ellentér
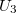 feszültség kb 7,4 V
feszültség kb 7,4 V
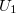 feszültséget 6,4 V
feszültséget 6,4 V
- A programozható tápegység feszültségtartományát állítsa High-ba, ekkor 60V a maximális kimeneti feszültség.
- Kapcsolja be az áramerősítő konvertert.
Az adatgyűjtőn állítsa be a mintavételezés jellemzőit és indítsa el a mérést. Különböző paraméterekkel végezze el a mérést, keresse meg a legjobb adatokat szolgáltató beállítást. Méréstechnikai szempontból és a mellékhatások miatt célszerű az árammaximumok távolságával számolni. A mérési adatok alapján állapítsa meg az ionizációs energiát.