Akusztooptikai fénydiffrakció vizsgálata

Szerkesztés alatt!

Elméleti összefoglaló

Bevezetés

A Brillouin által megjósolt akuszto-optikai kölcsönhatást 1932-ben mutatta ki Debye és Sears. Az effektus felhasználását, vagyis akuszto-optikai elven működő eszközök kifejlesztését és ezek alkalmazását a kollimált, monokromatikus fényforrások, a lézerek elterjedése tette lehetővé. Akuszto-optikai eszközök működnek lézeres sornyomtatóban, nagyfelbontású fénymásoló berendezésekben, egyes spektrométerekben, és olyan analóg műveletvégző optikai rendszerekben, amelyek nagysebességű (a digitálisnál gyorsabb) Fourier-transzformáció, illetve konvolúció képzésre alkalmasak.

A továbbiakban megismerkedünk az akuszto-optikai eszközök működésének megértéséhez szükséges alapfogalmakkal, és az akuszto-optikai kölcsönhatás néhány tulajdonságával.

Elméleti alapok

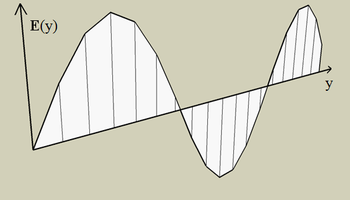
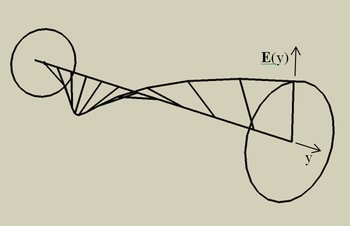
A fény elektromágneses hullám, melyben az E elektromos térerősség és a B mágneses indukcióvektor periodikus változása a terjed. Ezek (vákuumban) a terjedési irányra egyenként és egymásra is merőlegesek. Lineárisan polarizált hullámról akkor beszélünk, ha a térerősség vektor a terjedési irány mentén végig egy meghatározott síkban marad (1. ábra). Polarizációs iránynak az elektromos térerősség vektor irányát nevezzük. Két egymásra merőlegesen polarizált hullám egymástól függetlenül terjed. Cirkulárisan poláros nyalábnak azt nevezzük, ha a térerősség amplitúdója állandó, de a végpontja a nyaláb mentén és időben is a terjedési irány körül forog (2. ábra). Általános esetben a nyaláb se nem lineáris, se nem cirkulárisan poláros, hanem elliptikusan poláros (a vektor forog, és az amplitúdója is változik), illetve lehet polarizálatlan is (ez az állapot pl. végtelen sok, véletlen kezdőfázisú lineárisan polarizált nyaláb összegeként képzelhető el).

1. ábra. Lineárisan polarizált hullám

Egy tetszőlegesen polarizált nyaláb leírható két jól megválasztott fázisú és amplitúdójú, egymásra merőleges lineáris polarizációjú nyaláb összegeként (pl. a cirkulárisan polarizált hullám két azonos amplitúdójú 90° fáziskülönbségű lineárisan polarizált nyaláb összege). Ugyanígy bázisként használható két ellentétes irányba forgó cirkulárisan polarizált hullám (pl. lineárisan poláros hullám két azonos amplitúdójú jobbra és balra cirkulárisan poláros hullám összege). A fényt a továbbiakban síkhullámnak tekintjük (ez legalábbis esetünkben elfogadható közelítés).

2. ábra. Cirkulárisan polarizált hullám

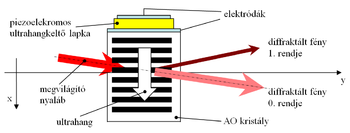
Akusztikus hullám esetén a közeg egyes pontjainak periodikus elmozdulása terjed tova, ami szintén vektormennyiség, és iránya az elmozdulás irányát, nagysága az elmozdulás nagyságát adja meg. Az elmozdulásvektor hely szerinti deriváltját (a közeg dV térfogatelemeinek relatív méretváltozását) nevezzük mechanikai deformációnak. A mérésben használt eszközben az akusztikus hullám transzverzális, amely az ultrahangkeltő és a kristály orientálásától, azaz a kristály lapjainak és a kristálytani tengelyek szögétől függ. Az ultrahang hullámot piezoelektromos egykristály lapkával hozzuk létre, amelyben a rákapcsolt nagyfrekvenciás (45 MHz, néhány volt amplitúdójú) feszültséggel arányos méretváltozás jön létre. Az ultrahangkeltő felépítése a 3. ábrán látható. A lapka által a generátorból felvett elektromos teljesítmény egyenlő az akusztikus hullám teljesítményével, ezért az ultrahang hullám teljesítményét a meghajtó áramkör elektromosan szabályozni tudja.

A két hullám (akusztikus-fény) a fotorugalmassági effektus révén hat kölcsön, melynek lényege, hogy a mechanikai deformáció törésmutató változást (Δn) hoz létre:

 

$\[\Delta n = \frac{1}{2}n^3pS\]$

(1)

ahol „n” a közeg törésmutatója, „p” a fotorugalmassági állandó és „S” a mechanikai deformáció (relatív méretváltozás).

3. ábra. Az ultrahangkeltő felépítése, és a törésmutató változás hullám

Akusztikus hullámok esetén a mechanikai deformáció periodikus a közegben:

 

$\[S = S_0\sin \Omega\left(t-\frac{x}{v}\right)\]$

(2)

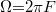ahol „$\setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%$” az akusztikus hullám körfrekvenciája $\setbox0\hbox{$\Omega {{=}} 2\pi F$}% \message{//depth:\the\dp0//}% \box0%$, „v” a hang terjedési sebessége, S0 az amplitúdója és „F” a frekvenciája. Ekkor az (1) egyenletnek megfelelően:

 

$\[\Delta n = n_0\sin \Omega\left(t-\frac{x}{v}\right)\]$

(3)

Vagyis egy, az x irányban haladó, az akusztikus hullám sebességével terjedő törésmutató változás hullámot kapunk: egy mozgó, szinuszosan modulált fázisrácsot (ld. következő fejezet).

Akuszto-optikai fénydiffrakció

Terjedjen a 3. ábrán látható közegben az akusztikus hullámra merőleges y-irányban egy elektromágneses hullám:

 

$\[\mathbf{E} = \mathbf{E}_0\sin \omega\left(t - \frac{yn}{c}\right) \]$

(4)

ahol „E” az elektromos térerősség, „c” a fénysebesség vákuumban, és „n” a közeg törésmutatója az elektromágneses hullám frekvenciáján. Látható, hogy a hullám fázisa:

 

$\[\varphi = \omega \left(t-\frac {y\cdot n(x)}{c}\right) = \omega t -\omega y\frac{n_0 \sin \Omega (t-\frac{x}{v}) }{c}\]$

(5)

függ a közeg törésmutatójától, vagyis a közegben terjedő akusztikus hullám a fotorugalmassági effektus következtében megváltoztatja az elektromágneses hullám fázisát. A fázisváltozás következtében a fényhullám elhajlik az akusztikus hullámon, amit akuszto-optikai fénydiffrakciónak nevezünk. Ennek egy speciális esete a Bragg-diffrakció, amikor a hanghullám (ill. a fázisrács) a fény terjedési irányában jóval szélesebb, mint az alkalmazott fény hullámhossza: ekkor az irányváltoztatás nélkül áthaladó megvilágító nyaláb (nulladrend) mellett csak egy diffrakciós rendet tapasztalunk, ami formálisan úgy írható le mintha a beeső fénynyaláb az akusztikus hullám fázisfelületeiről reflektálódna. Viszont ha a rács „vékony” (a hullámhosszakhoz viszonyítva) akkor megjelennek ±1, ±2, … rendek is. Az akuszto-optikai fénydiffrakció általános tárgyalása messze túlmutat a mérés anyagán, ezért a továbbiakban csak az akuszto-optikai Bragg-diffrakcióval foglalkozunk. Bragg-diffrakció tehát akkor jön létre, ha a) az akusztikus hullám y-irányban sokkal „vastagabb”, mint a kölcsönhatásban résztvevő hullámok hullámhossza, b) a beesés szögére (α) teljesül az ún. Bragg-feltétel:

 

$\[2\Lambda \sin \alpha = \lambda \]$

(6)

ahol „\lambda

\[” a fény hullámhossza a kristályban, „$\Lambda$” az ultrahang hullámhossza, „α” nyaláb és a fázissík által bezárt szög (ld. [[#fig:4|4. ábra]]). Ezt átrendezve kapjuk:
{{eq|\sin \alpha {{=}} \frac {\lambda}{2\Lambda} |eq:7|(7)}}
Ez a feltétel abból adódik, hogy a szomszédos fázisfelületekről a tükrözési törvénynek megfelelően visszaverődő nyalábok konstruktívan interferáljanak, azaz az úthosszkülönbség épp az optikai hullámhossz legyen. A jelenség megértéséhez a [[#fig:4|4. ábrán]] látható az akusztikus hullámból két szomszédos fázissíkról történő fényvisszaverődés.
{|  cellpadding="5" cellspacing="0" align="center"
|-
| {{fig|AO_04.png|fig:3|4. ábra. Akuszto-optikai Bragg-diffrakció}}
|}
A fény f frekvenciája nem változik meg a kristályba való belépéskor, ám megváltozik az akuszto-optikai diffrakció során, mégpedig az F akusztikus frekvenciával ($f_d {{=}} f \pm F$). Mivel azonban F<

PDF formátum

Akusztooptikai fénydiffrakció vizsgálata