Holográfia

A lap szerkesztés alatt!

Bevezetés

Mint az közismert, az ember térbeli látással rendelkezik. Ez részben abból adódik, hogy két szemmel sztereo látásra van módunk, azaz testünk vagy szemünk mozgatása nélkül is korábbi tapasztalataink alapján el tudjuk helyezni a térben az érzékelt tárgyakat, mivel két szemünk eltérő képet lát. Azonban még egy szemmel is lehetőségünk van bizonyos mértékben a térbeliség megítélésére, hiszen a különböző távolságban található tárgyakat csak akkor látjuk élesen, ha szemünk ún. akkomodációs, fókuszállítási képességét használjuk. Különböző távolságokra fókuszálva, és figyelve a tárgyak képének változását ezen a módon is térbeli képet alkothatunk környezetünkről. Tehetjük ezt annak ellenére, hogy érzékelőnk - a szem retinája - csak kétdimenziós.

Az általunk látottak rögzítésének egyik elterjedt módja a fényképezés. Ekkor a látáshoz hasonlóan a valóságos tárgyakat egy kétdimenziós felületre képezzük valamilyen optikai rendszer segítségével. Ha az elkészült fényképet nézzük, akkor a valóság szemléléséhez képest még két szemmel sem látunk ahhoz hasonló térbeli hatást. Ha különböző távolságokra fókuszálunk, legfeljebb a fényképet láthatjuk életlenül. A fénykép tehát kevesebb információt tartalmaz, mint amiről készítettük, a valóságban rendelkezésre álló információk egy része nem rögzült.

A hiányzó információ pedig nem más, mint a fény fázisa, ugyanis az érzékelők, detektorok csak a fény intenzitását észlelik. A holográfia újítása - amelyet Gábor Dénesnek köszönhetünk (1947), és amelyért Nobel-díjat kapott (1971) - éppen az, hogy közvetett módon mégis lehetővé teszi egy hullám fázisának rögzítését annak ellenére, hogy a holográfia is a fotónegatívokéhoz hasonló elvű képrögzítést alkalmaz. A holográfia „trükkje”, hogy a fázisváltozást intenzitásváltozássá változtatja/kódolja, azaz a detektorok számára is érzékelhetővé teszi. A kódolás megvalósítására az interferencia jelensége alkalmas, amelynél az eredő kép intenzitásának ingadozásai az interferáló fényhullámok fáziskülönbségétől függenek. A megvalósításhoz tehát a rögzítendő tárgyról kiinduló hullámon kívül egy másik hullámra is szükség van. A siker további feltételei, hogy a két hullám interferenciaképes legyen, ehhez nagy koherenciájú fényforrásokra (lézerekre) van szükség, valamint hogy az érzékelő felbontása elegendően nagy legyen ahhoz, hogy az interferenciaképet rögzíteni tudja. De mire jó egy ilyen interferenciamező? Amint azt alább látni fogjuk, a kidolgozott hologramlemez megfelelően megvilágítva a diffrakció révén úgymond rekonstruálja a kérdéses tárgyról szórt fény intenzitás és fáziseloszlását egyaránt, így a látvány teljesen háromdimenziós lesz. A hullámok fázisának rögzítése azonban nem csak érdekes látványt eredményezhet, hanem jónéhány optikai mérési eljárást is lehetővé tesz.

Jelen mérés célja: négy kisebb méretű és eltérő típusú hologram készítésén keresztül elsajátítani a hagyományos (analóg) holográfia gyakorlati alapjait, és megismerkedni két konkrét méréstechnikai alkalmazással: a holografikus interferometriával és a holografikus optikai elemek fogalmával.

Elméleti összefoglaló

Transzmissziós hologram készítése és rekonstrukciója

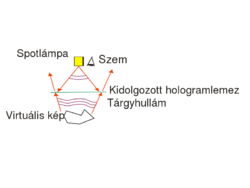
Az ún. fehérfényű látványhologramok szemlélésnek elrendezése nagyjából mindenki előtt ismert kiállítások révén: a kidolgozott hologramlemezt erős pontszerű fényforrással világítják meg, pl. spotlámpával. Azonban történetileg nem ez a hologramtípus az első, és az alapjelenség illetve a készítés megértéséhez sem ez a legalkalmasabb típus.

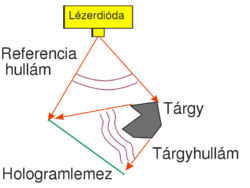
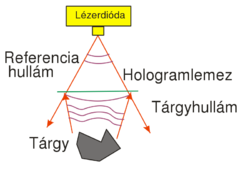
Hologram készítésének egyik lehetséges elrendezését mutatja az 1/a. ábra. Ezzel az elrendezéssel ún. transzmissziós off-axis hologram készíthető. Fényforrásnak lézerdiódát használunk, mely nagyfokú koherenciája révén biztosítja az interferenciaképességet. Ehhez továbbá ki kell zárni más természetes és hagyományos fényforrásokat, tehát a tárgyat külön meg kell világítani a lézerfénnyel. A diódalézer fénye nyalábformáló előtétlencse nélkül kb. ellipszis keresztmetszetű nyalábként tágul (divergens), így a tárgy- és referenciahullám úgy hozható létre, hogy a nyaláb egy része közvetlenül, a másik fele pedig a tárgyról szóródva jut a hologramlemezre, és ott interferálnak.

1/a. ábra: Transzmissziós off-axis hologram rögzítése

1/b. ábra: A virtuális kép rekonstrukciója

1/c. ábra: A valós kép rekonstrukciója

Ez a negatív filmektől eltérően többnyire szilárd hordozóra (pl. üveglap) felvitt nagy felbontású fényérzékeny réteget jelent. A hologramlemezek térbeli felbontása egy-két nagyságrenddel nagyobb, mint a színes negatív filmeké! Az interferenciakép, az ún. holografikus rács akkor rögzíthető jó minőségben, ha a két találkozó hullám intenzitásának aránya, valamint együttes intenzitásuk, és az exponálás ideje is megfelelő. Mivel az expozíciós idők másodperc vagy perc nagyságrendűek is lehetnek, arról is gondoskodni kell, hogy az interferenciakép és a hologramlemez egymáshoz képest ne mozogjon/rezegjen, ezért az egész elrendezést speciális optikai asztalra szokás helyezni, amely rezgésmentes, és kellő merevségű, valamint más zavaró hatásokat is ki kell zárni (pl. légáramlatok, háttérfény). Érdemes megjegyezni, hogy az 1/a. ábrán látható elrendezésben nem található a fényképezésnél vagy a látásnál meglévő leképező lencse. Ez azt is jelenti, hogy egy-egy tárgypontról a hologramlemez egészére szóródik fény, nincs tehát 1-1 megfeleltetés („leképezés“) a tárgypontok és a fényérzékeny lemez pontjai között (mint a hagyományos fényképezésnél). Mivel ebben az elrendezésben a tárgy és a referencia hullám jelentős szöget zár be egymással, ezért hívjuk off-axis hologramnak.

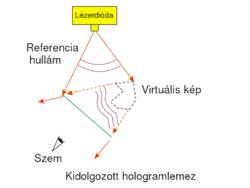
Az így exponált hologramlemezt típusától függően esetleg még elő is kell hívni, ami egy többlépéses vegyi kidolgozás, ezáltal rögzül rajta tartósan a kép. Ezen a képen azonban eltérően egy fényképtől önmagában nem látható semmi, ami az eredeti tárgyra hasonlítana, pl. egy negatív kicsinyített képmás, mint a fényképezésnél. Ez nem is csoda, hiszen a tárgy felől érkező hullámot a referenciával módosítottuk, és leképezést sem alkalmaztunk. A megfelelő kép előállításához egy másik lépésre, a hologram rekonstrukciójára van szükség, ami amolyan „dekódolás” is: ez látható az 1/b. ábrán. Az elrendezésből a tárgyat elhagyva csak a referencia hullám jut a lemezre, és ott diffraktálódik a létrejött rácsozaton, mivel azon a kidolgozás módjától és a lemez típusától függően vagy sötét és világos részek váltják egymást (amplitúdó hologram), vagy kisebb és nagyobb törésmutatójú részek (fázis hologram).

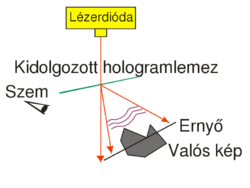
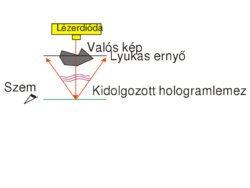
A tárgy virtuális térbeli képe (amely ernyőn nem fogható fel) annak eredeti helyén jelenik meg, ha a lemez másik oldaláról szemlélődünk, továbbá ideális esetben azonos méretben és irányításban látható. Különböző irányokból másként látszik, tehát két szemmel nézve sztereo képet ad. A különböző mélységben található részekre rá lehet fókuszálni szemmel, így a térbeli mélysége is megvan. Azonban van néhány korlátozó eltérés is: mivel mind a hologram rögzítéséhez, mind a rekonstrukcióhoz monokromatikus lézer fényforrást kell használni, a holografikus kép eredendően egyszínű, valamint a sík hologramlemez véges mérete miatt a virtuális tárgy többnyire nem járható körbe, a lemez mérete korlátozó ablakot jelent. Mivel a szemünkbe az ábra elrendezése szerint jutó fény áthaladt a lemezen (a referencia megvilágítás a lemez másik oldalán van, mint a szem), ezért ez a virtuális kép transzmissziós. A diffrakció révén azonban létrejön egy a rajzon fel nem tüntetett valós (ernyőn felfogható) kép is a lemez átellenes oldalán, amely így szintén transzmissziós. Mivel a hologram off-axis, a kétféle kép nyalábja különböző irányba terjed. Ha a valós képet jól kivehető módon szeretnénk megfigyelni, az 1/c. ábrán látható rekonstrukciós elrendezését használhatjuk. Ekkor egy keskeny lézersugárral világítjuk át a hologramlemez valamely kis darabját, és a geometriát úgy választjuk meg, hogy a megvilágító lézersugár a hologramlemezhez képest pont azzal az iránnyal ellentétes irányban haladjon, amelyben a felvételkor használt referencianyaláb érte a lemezt.

A holográfia elvi háttere

Az eredeti tárgyhullám másának visszanyerése matematikailag az alábbi egyszerű módon látható be amplitúdó hologram esetére. Tekintsük a fényhullám amplitúdóját a hologramlemez közvetlen környezetében. Felvételkor a lemezhez érkező két hullám komplex amplitúdója legyen az 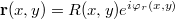$\setbox0\hbox{$\mathbf{r}(x,y)=R(x,y)e^{i\varphi_r(x,y)}$}% \message{//depth:\the\dp0//}% \box0%$ referencia, és a 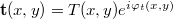$\setbox0\hbox{$\mathbf{t}(x,y)=T(x,y)e^{i\varphi_t(x,y)}$}% \message{//depth:\the\dp0//}% \box0%$ tárgyhullám, ahol R és T valós értékű amplitúdók. A referenciahullám R(x,y) erőssége a lemeznél már csak lassan változik, gyakorlatilag R állandónak tekinthető. A lemezt exponáló intenzitáseloszlás, azaz interferenciakép

$\[I_{\rm{exp}}=|\mathbf{r}+\mathbf{t}|^2 = R^2+T^2+\mathbf{rt^*+r^*t}\]$

formában írható le, ahol a $\setbox0\hbox{$*$}% \message{//depth:\the\dp0//}% \box0%$ a komplex konjugálást jelöli. Ideálisnak tekintett, lineáris átvitelű hologramlemez esetén a kidolgozott lemez feketedése ennek állandószorosa lesz, így a lemez $\setbox0\hbox{$\tau$}% \message{//depth:\the\dp0//}% \box0%$ fényáteresztő képessége

$\[\tau=1–\alpha I_{\rm{exp}}\]$

alakú, ahol $\setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%$ egy anyagállandó és az expozíciós idő szorzata. Rekonstrukciókor a hologramlemezt az eredeti referenciahullámmal átvilágítva közvetlenül a lemez mögött a komplex amplitúdó

$\[\mathbf{a} = \mathbf{r}^*\tau=\mathbf{r}(1–\alpha R^2–\alpha T^2)–\alpha\mathbf{r}^2\mathbf{t}^*–\alpha R^2\mathbf{t}\]$

alakot ölt. Ennek első tagja a referenciahullám áthaladó hányada, második 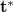$\setbox0\hbox{$\mathbf{t}^*$}% \message{//depth:\the\dp0//}% \box0%$-al arányos tagja egy fókuszálódó (ez 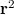$\setbox0\hbox{$\mathbf{r}^2$}% \message{//depth:\the\dp0//}% \box0%$ miatt lehet) konjugált kép, harmadik t-vel arányos tagja pedig az eredeti tárgyhullám mása (vegyük észre, hogy az arányossági tényezők mind valós állandók!). Ez virtuális képet ad, mivel közvetlenül a hologramlemez mögötti síkdarabon így ugyanolyan hullámtér áll elő (fázisát is tekintve, hisz t komplex), mint az eredeti tárgyról érkező fény esetén. A (3) összefüggést épp ezért a holográfia alapegyenletének is nevezik. 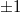Off-axis hologram esetén ez a három elhajlási rend ($\setbox0\hbox{$0$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\pm 1$}% \message{//depth:\the\dp0//}% \box0%$) irányban szétválik, ellenkező esetben viszont nem. (Megjegyzés: ha a lemez viselkedése nem teljesen lineáris, megjelenhetnek magasabb diffrakciós rendek is)

Reflexiós hologram készítése és rekonstrukciója

A fejezet elején említett fehérfényű látványhologramok az eddig tárgyalt típustól abban térnek el, hogy in-line elrendezésűek, azaz a nyalábok a lemez normálisával nulla vagy kis szöget zárnak be, valamint reflexiós elrendezésűek: a referencia és a tárgynyaláb a lemez átellenes oldaláról érkezik, rekonstrukciókor pedig a megvilágítás és a megfigyelés van azonos oldalon. A reflexiós hologramok rögzítésének elrendezését a 2/a. ábra mutatja. Ilyen hologramok esetén is megfigyelhető valós és virtuális rekonstruált kép, az ezekhez tartozó elrendezés a 2/b. és 2/c. ábrán látható.

2/a. ábra: Refelxiós hologram rögzítése

2/b. ábra: A virtuális kép rekonstrukciója

2/c. ábra: A valós kép rekonstrukciója

Fehér fényben ezek a hologramok azért tekinthetők meg, mert kb. 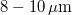$\setbox0\hbox{$8-10\,\rm{\mu m}$}% \message{//depth:\the\dp0//}% \box0%$ vagy még vastagabb fényérzékeny réteget tartalmazó lemezre készülnek, így már ún. vastag hologramnak tekinthetők a hullámhosszhoz képest. A vastag diffrakciós rácsok ún. Bragg-effektust mutatnak: a fehér fényt alkotó hullámokból csak a rögzítésnél használthoz közeli hullámhosszakon diffraktálnak jelentősen, így „szelektálnak” a színek között, továbbá érzékenyek a rekonstrukciónál alkalmazott megvilágítás irányára is, amelynek nagyjából azonosnak kell lennie a felvételkori referencia nyaláb irányával, ez pedig egy irányszelektivitást jelent. Ez utóbbi tulajdonságnak köszönhetően vastag hologramlemezbe többet is lehet exponálni úgy, hogy a rögzített képek közül lényegében mindig csak egy rekonstruálódik a megvilágítás irányától függően. (Minél vastagabb, „térfogatibb” egy hologram, annál szelektívebb, így szélsőséges esetben rengeteg hologram - vagyis kép, azaz akár bináris adat - rögzíthető a fényérzékeny anyag egyazon térfogatába. Ez az alapja a holografikus adattárolásnak.)

Holografikus interferometria

Mivel a rekonstruált tárgyhullám komplex amplitúdóját maga az eredeti tárgy határozza meg, pl. annak alakja, felületi minősége, így a hologram ezekről is tárol valamennyi információt. Ha egyetlen tárgyról annak két különböző állapotában készítünk egy-egy hologramot ugyanarra a lemezre egymás után azonos referenciával, az így kapott lemezt kétexpozíciós hologramnak hívjuk:

$\[I_{12}=|\vec r+\vec t_1|^2+|\vec r+\vec t_2|^2=R^2+T^2+\vec r\vec t_1^*+\vec r^*\vec t_1+R^2+T^2+\vec r\vec t_2^*+\vec r^*\vec t_2=2R^2+2T^2+(\vec r\vec t_1^*+\vec r\vec t_2^*)+(\vec r^*\vec t_1+\vec r^*\vec t_2)\]$

(Itt feltételeztük, hogy a tárgynyalábnak csak a fázisa változott meg érdemben, T valós amplitúdója nem, továbbá az indexek az állapotokat jelölik.) Rekonstrukciókor a két állapot egyidejűleg jelenik meg:

$\[\vec a_{12}=\vec r\tau=\vec r(1-\alpha I_{12})=\vec r(1-2\alpha R^2-2\alpha T^2)-\alpha \vec r^2(\vec t_1^*+\vec t_2^*)+\alpha R^2(\vec t_1+\vec t_2)\]$

Mérési feladatok

Elmozdulásmező vizsgálata real-time holografikus interferometriával reflexiós elrendezésben

változni fog