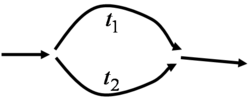Interferencia és dekoherencia nanoszerkezetekben

Interferencia-kísérletek hat nagyságrenddel kisebb skálán

A fizikában régóta ismertek az interferencia-kísérletek, melyeknek egy emblematikus példája az 1. ábrán szemléltetett kétrés kísérlet. Ha fény két közeli résen halad keresztül, a rések mögé helyezett ernyőn interferencia-képet látunk, azaz az ernyőn látható intenzitásprofil nem egyezik meg az egyik illetve a másik rés kitakarásakor kapott intenzitások összegével, hanem azon tartományokban ahova a két résen keresztül azonos fázissal érkezik a hullám erősítést, ahol pedig ellentétes (180 fokkal eltolt) fázissal, ott kioltást tapasztalunk. Természetesen ugyanez a jelenség a legkülönbözőbb közegekben megfigyelhető a vízhullámoktól a hanghullámokig.

1. ábra.

A modern fizika fejlődésével az interferencia-kísérletek újabb értelmezést kaptak, hiszen jól demonstrálták a részecske hullám dualitást. Ha az 1. ábrán szemléltetett kísérletben nagyon kis fényintenzitást, és nagyon érzékeny ernyőt használunk, akkor először véletlenszerű felvillanásokat látunk az ernyő különböző pontjain, mely a fény részecske-természetét támasztja alá. Ha viszont sokat várunk, akkor a véletlenszerű felvillanásokból kirajzolódik a jól ismert interferencia-kép (lásd 2. ábra).

1. ábra.

További érdekesség, hogy ha a két rés mellé detektorokat helyezünk és próbáljuk megállaítani, hogy a fényt alkotó fotonok éppen melyik résen haladnak keresztül, akkor azt tapasztaljuk, hogy minél pontosabban detektáljuk a résen áthaladó fotonokat, annál inkább elvész az interferenciakép. Azaz akár egyetlen foton is képes mindkét résen áthaladva önmagával interferálni, viszont ha megmérjük, hogy merre ment a foton, akkor az interferencia megszűnik.

Az elmúlt évtizedekben a nanofizika fejlődésének köszönhetően a kétrés kísérlethez hasonlóan izgalmas interferenciakísérleteket mintegy 6 nagyságrenddel kisebb méretskálájú nanoáramkörökben is sikerült megvalósítani, ebbe a témakörbe nyújtunk betekintést a következőkben.

1. ábra.

Aharonov Bohm gyűrű

1. ábra.

Az Aharonov Bohm gyűrű két karján haladó hullámok a vektorpotenciál hatására is felvesznek fázist. A vezetőképesség a közbezárt fluxus (

\setbox0\hbox{\setbox0\hbox{$\Phi$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex>) fluxuskvantum (

\setbox0\hbox{\setbox0\hbox{$\Phi_0=h/e$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>) szerint periodikus függvénye:

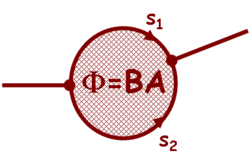
$\[G\sim T = |t_1+t_2|^2 = \left| e^{i k_F s_1 + \frac{i e}{\hbar} \int \limits_1 \vec{A} \mathrm{d}\vec{s}} + e^{i k_F s_2 + \frac{i e}{\hbar} \int \limits_2 \vec{A} \mathrm{d}\vec{s}}\right|^2 = \]$

$\[2+2\cdot cos\left(k_F(s_1-s_2)+\frac{e}{\hbar} \oint \vec{A} \mathrm{d} \vec{s}\right) = 2+2\cdot cos(\delta_0 + 2 \pi \Phi/\Phi_0)\]$

Alacsony hőméréskleten látszik az oszcilláció a mágneses tér függvényében, magasabb hőmérsékleten azonban elmosódik.

Az interferenciakép eltűnésének az okai:

• Környezet miatti dekoherencia
• Hőmérsékleti miatti fázis kiátlagolódás

1. ábra.

Hőmérsékleti miatti koherenciavesztés

1. ábra.	1. ábra.

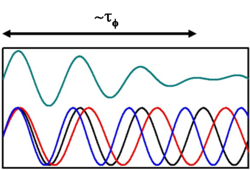
Véges hőmérsékleten a Fermi energia körüli kT tartományban különböző energiájú elektronok propagálnak. Koherens összeadás esetén is a fázisok kiátlagolódnak!

$\[\sim \int \limits_{E_F-kT/2}^{E_F+kT/2} e^{i E t / \hbar} \mathrm{d}E\]$

A nanoszerkezeten az elektronok átlagosan

\setbox0\hbox{\setbox0\hbox{$\tau_c$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex> idő alatt haladnak át. Az ehhez tartozó karakterisztikus energia: Thouless energia,

\setbox0\hbox{\setbox0\hbox{$E_T=\hbar/\tau_c$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex>

\setbox0\hbox{\setbox0\hbox{$\longrightarrow$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex>

\setbox0\hbox{\setbox0\hbox{$\sim kT > E_T$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex> hőmérsékleten lesz jelentős ez a kiátlagolódás

Környezet miatti koherenciavesztés

1. ábra.

• Alsó ágon haladó eletronhullám:

  \setbox0\hbox{\setbox0\hbox{$|1\rangle$}%
  

\message{//depth:\the\dp0//}% \box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>

• Felső ágon haladó eletronhullám:

  \setbox0\hbox{\setbox0\hbox{$|2\rangle$}%
  

\message{//depth:\the\dp0//}% \box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>

Teljes hullámfügvény:

$\[|\Psi\rangle = (\alpha|1\rangle + \beta|2\rangle)|\Phi_{env}\rangle\;\;\longrightarrow\;\;\alpha|1\rangle|\Phi_{env1} + \beta|2\rangle|\Phi_{env2}\]$

Transzmissziót mérünk: (T operátor csak az elektron hullámfüggvényekre hat, a környezetre nem!)

$\[\langle\Psi|T|\Psi\rangle = |\alpha|^2 \langle 1|T|1\rangle + |\beta|^2 \langle 2|T|2\rangle + \alpha^*\beta \langle 1|T|2\rangle \langle \Phi_{env1}|T|\Phi_{env2}\rangle + \beta^*\alpha \langle 2|T|1\rangle \langle \Phi_{env2}|T|\Phi_{env1}\rangle\]$

Ha

\setbox0\hbox{\setbox0\hbox{$\langle \Phi_{env1}|\Phi_{env2}\rangle \rightarrow 0$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>, akkor elveszik az interferencia!

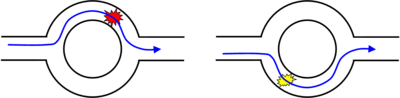
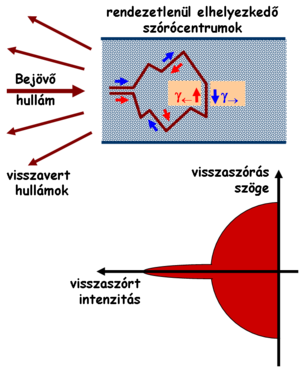
• Azaz ha a felül és alul haladó parciális elektronhullám különböző nyomot hagy a környezetben, akkor nem látunk interferenciát. Erre jó példa a fonon szórás, mely a hőmérséklet növelésével egyre jelentősebb dekoherenciához vezet.

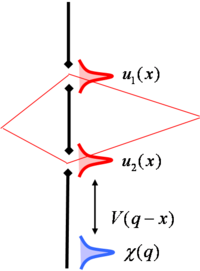
Egyszerű példa (Stern, Aharonov, Imry)

1. ábra. Vezetőképesség fluktuációk

Az alsó ágon haladó részecske hullámfügvénye megváltozik a kölcsönhatás miatt:

\setbox0\hbox{\setbox0\hbox{$|u_2(x)|\cdot e^{-i(E+V(q-x))\cdot t/\hbar}$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>

• A kölcsönhatás ideje alatt felszedett fázis:

  \setbox0\hbox{\setbox0\hbox{$\Phi$}%
  

\message{//depth:\the\dp0//}% \box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>.

• q bizonytalansága miatt a fázis is bizonytalan:

  \setbox0\hbox{\setbox0\hbox{$\Delta \Phi = \frac{1}{\hbar} \frac{\partial V}{\partial q} \cdot \Delta q \cdot t$}%
  

\message{//depth:\the\dp0//}% \box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>

• Ha a fázisbizonytalanság nagy lesz, elveszik az interferencia:

$\[\Delta \Phi > 1 \Leftrightarrow \frac{\partial V}{\partial q} \cdot t > \frac{\hbar}{\Delta q}\]$

Töltött részecske, mely csak az alsó ágon áthaladó elektronnal hat kölcsön (a felső ágon haladó elektronnal elhanyagolható a kölcsönhatás). Helykoordináta:

\setbox0\hbox{\setbox0\hbox{$q$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex>, helybizonytalanság:

\setbox0\hbox{\setbox0\hbox{$\Delta q$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>

• Ha alul halad az elektron, a töltött részecske gyorsul az erő hatására. Kölcsönhatás ideje (t) alatt az impulzusváltozás:

  \setbox0\hbox{\setbox0\hbox{$\delta p = \frac{\partial V}{\partial q}\cdot t$}%
  

\message{//depth:\the\dp0//}% \box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>

• Ha az impulzus változás nagyobb az impulzus bizonytalanságnál,akkor a részecske tárolta az "útinformációt":

$\[\delta p > \Delta p \Leftrightarrow \frac{\partial V}{\partial q}\cdot t > \frac{\hbar}{\Delta q} \Leftrightarrow \langle\chi_1|\chi_2\rangle<<1\]$

Ugyan az a két feltétel! Ugyanakkor veszik el az interferencia, amikor a környezet állapota megkülönbözethetővé válik alul illetve felül haladó elektron esetén!

Környezet miatti koherenciavesztés Aharonov Bohm gyűrűben

Ha a kétrés kísérletben megmondható, hogy az elektron melyik résen haladt át (nyomot hagy a környezetében)

\setbox0\hbox{\setbox0\hbox{$\rightarrow$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex> interferencia megszűnik.

Interferométer: Aharonov - Bohm elrendezés QDot-tal az egyik ágban.

„Útvonal” detektor = QDot + mellette kvantum vezeték (QPC): a Dotban lévő elektron visszaszórást okoz QPC-ben, minél több e-t szór vissza a QPC-ban, annál nagyobb nyomot hagy a környezetén.

Környezet miatti koherenciavesztés: a környezetben minnél nagyobb nyomot hagy az

\setbox0\hbox{\setbox0\hbox{$e \rightarrow |\langle \Phi_{env1}|\Phi_{env2}\rangle|$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex> csökken

\setbox0\hbox{\setbox0\hbox{$\rightarrow$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex> az interferencia láthatósága csökken (láthatóság:

\setbox0\hbox{\setbox0\hbox{$\nu = Ampl/Avg$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex>)

• Detektor „érzékenységét” QPC-ra adott (

  \setbox0\hbox{\setbox0\hbox{$V_d$}%
  

\message{//depth:\the\dp0//}% \box0%

}%

\message{//depth:\the\dp0//}% \box0%

</latex>) feszültség növelésével javíthatjuk:

\setbox0\hbox{\setbox0\hbox{$I_{QPC}$}%
\message{//depth:\the\dp0//}%
\box0%

}%

\message{//depth:\the\dp0//}% \box0% </latex> nő, több elektront tud visszaszórni.

• A detektor érzékenységének a növelésével az interferencia láthatósága csökken!

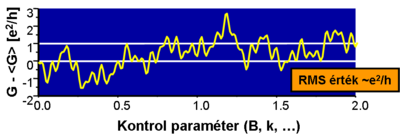
Vezetőképesség fluktuációk

1. ábra. Vezetőképesség fluktuációk

1. ábra. Vezetőképesség fluktuációk

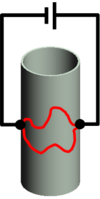
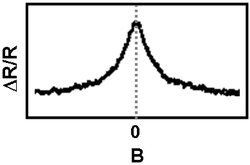
Gyenge lokalizáció

1. ábra. Vezetőképesség fluktuációk

1. ábra. Vezetőképesség fluktuációk

1. ábra. Vezetőképesség fluktuációk