Lock-in programozás, kvarcszenzor vizsgálata
A mérés célja
A mérés célja a későbbi Szupravezetés c. laboratóriumi gyakorlat során is használt Stanford Research Systems SR830 típusú digitális lock-in erősítő használatának és programozásának megismerése, egy atomi erő mikroszkópokban is használt kvarc szenzor vizsgálata ill. termikus zaj jelenségének tanulmányozása a lock-in erősítő segítségével.
Ennek érdekében először gyakorló mérésként párhuzamos LC kör rezonancia görbéit vesszük fel, majd hasonló elrendezésben a kvarc oszcillátor éles rezonanciáját vizsgáljuk. Végül ellenállások termikus zajának méréséből határozzuk meg az abszolút hőmérsékletet.
Órákban használt kvarcoszcillátor nanofizikai alkalmazása
A Lock-In erősítő kiválóan alkalmas különböző áramköri elemek frekvenciafüggő impedanciájának vizsgálatára. Egy párhuzamos LC körön végzett gyakorló mérések után a laborgyakorlaton a kvarcórákban általánosan használt kvarc oszcillátor (tuning fork) viselkedését vizsgáljuk. A kvarc oszcillátor egy hangvillára hasonlít (1. ábra), sajátfrekvenciája 32768 Hz. A kvarc piezoelektromos viselkedésének köszönhetően a hangvilla rezgését elektromosan, az oszcillátorra párologtatott elektródákra adott feszültséggel lehet gerjeszteni. Az oszcillátor kiemelkedően jó jósági tényezővel rendelkezik, a rezonanciacsúcs szélessége csak pár hertz.
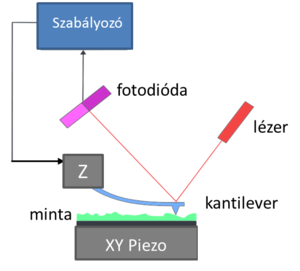
Az atomerő mikroszkóp érzékelője az úgynevezett kantilever: egy laprugó a végén egy hegyes tűvel. Az alagútmikroszkóppal ellentétben az alagútáram helyett a minta és a tű közötti erőhatást mérik, amihez a kantilever lehajlását detektálják. Ezt a leggyakrabban a 8. ábrán vázolt elven: a laprugóról visszavert lézersugár és egy fotodetektor segítségével végzik.
 |
| 8. ábra. Tipikus atomerő mikroszkóp működési elve, forrás Wikipedia |
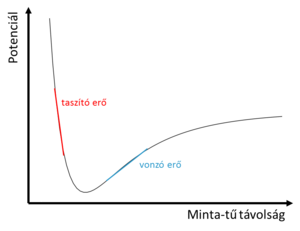
Az atomerő mikroszkóp hátránya az alagútmikroszkóphoz képest, hogy míg az alagútmikroszkóp esetén a távolsággal exponenciálisan változó alagútáramot mérve nagyon pontosan detektálható a minta-tű távolság változása, addig az atomerő mikroszkóp esetén a minta atomjai és a tű között fellépő - tipikusan nN nagyságrendű - erő sokkal kevésbé érzékeny a minta-tű távolságra valamint nem is monoton módon változik. A tűvel a felülethez közeledve először az indukált dipólus-dipólus kölcsönhatásból származó, nagy hatótávolságú, vonzó van der Waals erő jelenik meg. Tovább közeledve a rövidebb hatótávolságú, kémiai kötésekből származó erő kezd dominálni, mely először vonzó, majd taszító hatást fejt ki a tűre (9. ábra).
 |
| 9. ábra. Potenciál a minta-tű távolság függvényében. |
A minta és a tű közötti erő mérése alapvetően két különböző elven, statikus illetve dinamikus üzemmódban valósítható meg. Statikus üzemmódban a tűt a minta felületéhez nyomják, az erő közvetlenül a laprugó lehajlásából határozható meg. Dinamikus üzemmódban a laprugót a rezonancia-frekvenciáján rezgetik, a minta és a tű közötti erőhatás következtében megváltozik a rezgés frekvenciája, fázisa, amplitúdója ezek egyikéből meghatározható az erő nagysága.
Az atomerőmikroszkóp mérési üzemmódjai tovább csoportosíthatóak aszerint, hogy a 9. ábrán vázolt potenciál melyik szakaszán végzik a mérést: a kisebb minta-tű távolsághoz tartozó taszító erőhatású tartományon mérve kontakt, a nagyobb minta-tű távolsághoz tartozó, vonzó erőhatással jellemezhető tartományon mérve nem kontakt üzemmódról beszélhetünk.
Statikus üzemmódban pásztázás közben úgy mozgatják a tűt, hogy a laprugó lehajlása állandó legyen. A minta és a tű közötti erőhatás annál pontosabban határozható meg, minél kisebb a laprugó rugóállandója. Azonban a felület közvetlen közelében nagy vonzó erő hat a tűre, ami azt a felületre rántja. Ezért statikus üzemmódot alkalmazva szinte mindig kontakt üzemmódban mérnek.
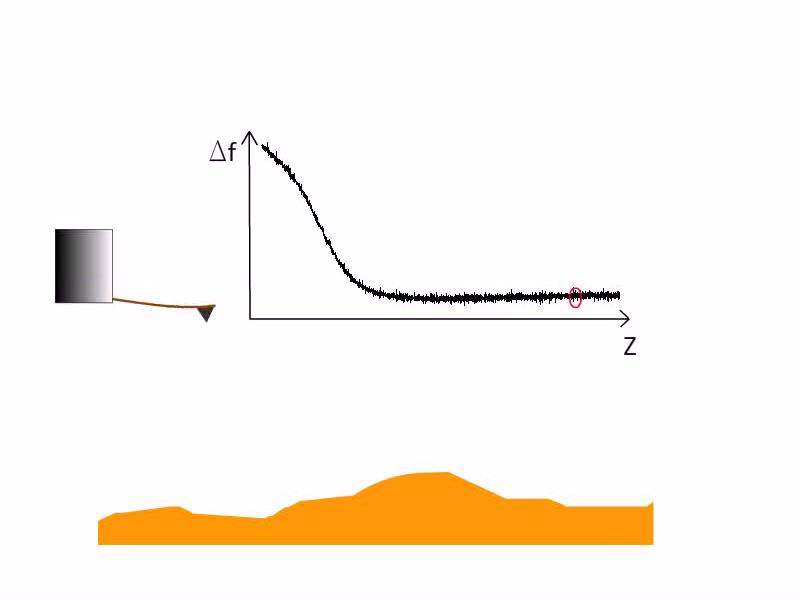
Nem kontakt üzemmódban a laprugót a rezonanciafrekvenciáján gerjesztik, a rezgés amplitúdója 10 nm-nél kisebb, akár néhány pm is lehet. A tűre ható erő elhangolja a rezonancia-frekvenciát, pásztázás közben úgy mozgatják a tűt, hogy mindig állandó legyen a frekvencia-eltolódás (10. ábra).
  |
| 10. ábra. Atomerő mikroszkóp működése nem kontakt, dinamikus üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. |
Szobahőmérsékleten mérve a legtöbb minta felszínén egy vékony folyadék film képződik, ami megnehezíti a nem kontakt üzemmódban történő mérést, erre a célra fejlesztették ki az úgynevezett tapping üzemmódot. Ebben az esetben a laprugót a rezonancia-frekvenciájához közel gerjesztik, a rezgés amplitúdója tipikusan 100-200 nm. A minta és a tű közötti erőhatás egyre csökkenti a rezgés amplitúdóját, ahogyan a tű közeledik a minta felületéhez. Pásztázás közben a laprugó rezgési amplitúdójára szabályozva mindig úgy mozgatják a tűt, hogy az amplitúdó állandó legyen.
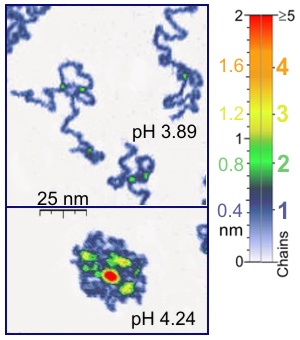
A 11. ábrán látható egy polimerláncról készült felvétel, tapping üzemmódban mérve.
 |
| 11. ábra. Polimerlánc atomerőmikroszkópos képe, forrás: Wikipedia |
A kereskedelmi forgalomban kapható atomerő mikroszkópok esetén leggyakrabban az előbbiekben ismertetett kantilevert használják érzékelőként. Speciális körülmények - például alacsony hőmérsékleten történő mérés esetén - problémát jelenthet a laprugó lehajlásának lézeres detektálása, sokkal kézenfekvőbb megoldás egy olyan érzékelő, amivel elektromos elven mérhetjük a minta és a tű között fellépő erőt. A hagyományos AFM kantilever helyett egy speciális, piezoelektromos elven működő érzékelő készíthető a kvarc órákban is használt hangvilla alakú kvarcoszcillátort alkalmazva (12. ábra).
 |
 |
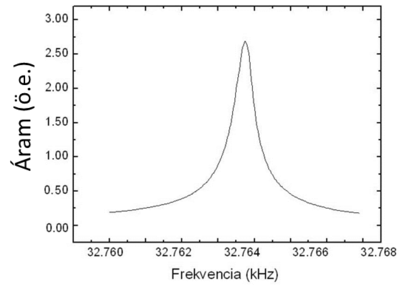
| 12. ábra. Kvarcórákban használt hangvilla alakú kvarcoszcillátor (bal oldal) és annak rezonancia-görbéje (jobb oldal), forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013. | |
A hangvilla alakú kvarcoszcillátort kvarcórákban, elektronikai áramkörökben használják órajel előállítására, olcsón beszerezhető - körülbelül 20 Ft/db. Az oszcillátor egy hangvilla alakú kvarc (Tuning Fork vagy röviden TF-nek is szokták nevezni), a legfontosabb jellemzője a rezonancia-frekvenciájának az értéke, névlegesen 32,768kHz. A kvarcot kontaktáló fém elektródák úgy vannak kialakítva, hogy elektromosan mind gerjeszteni mind a rezgést detektálni csak egyetlen rezgési módusban lehet: amikor az ágak a hangvilla síkjában, tükörszimmetrikusan rezegnek. A kontaktusokra váltakozó feszültséget kapcsolva, a kristály periodikusan deformálódik, rezgésbe jön. Amikor a rákapcsolt váltakozó feszültség frekvenciája megegyezik a kvarckristály anyagától és méreteitől függő rezonancia-frekvenciájával, a rezgési amplitúdó sokszorosára nő. A rezgés detektálásához a kvarcoszcillátoron folyó áramot mérjük, ami a hangvilla ágainak sebességével arányos, a rezonancia-frekvenciánál maximuma van (12. ábra, jobb oldal). Minél kisebb a csúcsnak a félérték-szélessége, annál pontosabban mérhető a rezonancia-frekvencia.
Az AFM érzékelőhöz a kvarcoszcillátor egyik ágára egy hegyes tűt ragasztunk, ez az érzékelő dinamikus módban történő mérést tesz lehetővé. A kvarcoszcillátort a rezonancia-frekvenciáján gerjesztjük, a tűt a felülethez közelítve a rezonancia-frekvencia eltolódik. Pásztázás közben úgy mozgatjuk a tűt a felületre merőlegesen, hogy a frekvencia-eltolódás mindig a kívánt minta-tű távolságnak megfelelő frekvencia-eltolódással egyezzen meg.
Mivel a minta és a tű közötti erőhatás lassan változik a minta-tű távolság függvényében, ezért atomerő mikroszkóppal nehezebb jó felbontást elérni mint alagútmikroszkóppal mérve. Ehhez jóval hegyesebb tűre van szükség, például elektrokémiai marásos eljárással hegyezhetünk tűt erre a célra.
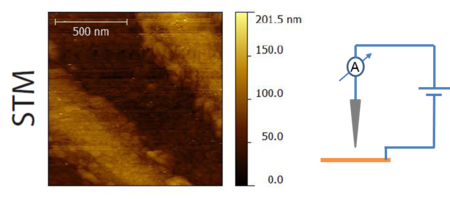
A 13. ábrán látható egy elektronsugaras litográfiával készült majd arannyal bevont felületű nanoszerkezeten történő mérés alagútmikroszkóp üzemmódban - az alagútáramra szabályozva, majd ezt követően ugyanazon a helyen atomerő mikroszkóp üzemmódban - a kvarcoszcillátor frekvencia-eltolódására, azaz a minta és a tű között fellépő erőre szabályozva. Mindkét esetben pár száz nm széles, párhuzamos csíkok láthatóak. Az alagútmikroszkóp felvételén a litográfiával készült csíkokon kívül finomabb struktúrák is megfigyelhetőek: párszor 10 nm méretű dombok, ezeket az atomerő mikroszkóp nem volt képes felbontani.
 |
|
| 13. ábra. Elektronsugaras litográfiával készült nanoszerkezeten történő mérés STM majd AFM üzemmódban, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013. |
A kvarc oszcillátor természetesen több rezgési módussal is rendelkezik, azonban az elektródák úgy vannak kialakítva, hogy csak a szimmetrikusan rezgő módust gerjesztik. Ezen módus sem erővel sem forgatónyomatékkal nem hat a rögzítési pontra, így gyengén csatolódik a külvilághoz.
A piezoelektromos tulajdonságokat az alábbi mátrixegyenlettel lehet leírni:
![\[ \left(\begin{matrix} z \\ Q \end{matrix}\right) = \left(\begin{matrix} k^{-1} & s \\ s & C \end{matrix}\right)\cdot \left(\begin{matrix} F \\ U \end{matrix}\right),\]](/images/math/b/e/2/be24417935c310c511be64aefebd61b0.png)
ahol 
a piezo elmozdulása a megfelelő tengely irányában, 
az elektródákon megjelenő töltés, 
a piezo által kifejtett erő, 
az elektródák közötti feszültség, 
a terheletlen (
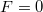) piezo elmozdulása egységnyi feszültség hatására, 
a rugóállandó zérus feszültségnél, 
pedig a kapacitás (egységnyi feszültségre eső töltésfelhalmozódás) 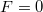mellet. Energiamegmaradási megfontolásból a fenti mátrix determinánsa 
, azaz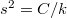 
. Ez alapján általánosan elmondható, hogy:
![\[Q=\alpha \cdot z,\]](/images/math/a/a/4/aa4a0c42e7d9d2bea5cd5b11f11bbc9d.png)
ahol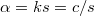 
.
Ha az oszcillátort egy egy szabadsági fokú rendszernek tekintjük (azaz csak a szimmetrikus rezgést vizsgáljuk) akkor a mozgás jól leírható az alábbi differenciálegyenlettel:
![\[m\ddot{z}=-kz-g\dot{z}+sU\]](/images/math/0/5/f/05fa4fa44971642600e5b4dd53a03ae9.png)
 |
| 1. ábra |
Termikus zaj szilárdtestekben
Különböző mennyiségek mérésénél általában a vizsgált mennyiség várható értékére vagyunk kíváncsiak, és a várható érték körüli fluktuációt zavaró tényezőnek tekintjük. Sok esetben viszont egy fizikai mennyiség "zaja" több információt hordoz a rendszerről mint maga a várható érték. A mérési gyakorlaton az egyik legalapvetőbb zajformát, az ún. termikus zajt tanulmányozzuk. A termikus zaj véges hőmérsékleten jelentkezik a különböző állapotok betöltésének termikus fluktuációi miatt. Egy fermionikus rendszerben egy állapot betöltési száma n=0,1 lehet. A betöltési szám várható értéke a Fermi függvény,
![\[\left< n \right> =f=\frac{1}{\mathrm{e}^{\frac{\epsilon-\mu}{k_B T}}+1}.\]](/images/math/f/5/0/f5028b4c93b1656982f996fda13bd196.png)
A betöltési szám szórásnégyzete:
![\[\left< \left(n-\left<n \right> \right)^2\right)=\left< n\right> -\left< n \right> ^2=f(1-f)=-k_B T\frac{\mathrm{d}f}{\mathrm{d}\epsilon},\]](/images/math/e/7/a/e7a80ca588fdd642172e63f8ad7f7c68.png)
ahol kihasználtuk, hogy fermionokra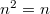 
. A kifejezést energia szerint kiintegrálva (
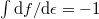) rögtön látszik, hogy a termikus zaj arányos a hőmérséklettel.
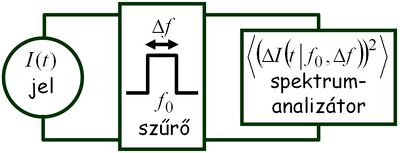
A zaj mértékének pontos megadásához először definiálni kell a zaj mérésére használt mennyiséget. Egy zajmérés kísérleti megvalósítása a következő ábrán szemléltethető:
 |
| 2. ábra |
A mért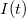 
jelből kiszűrjük az 
frekvencia körüli 
sávszélességű tartományt, és az így kapott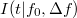 
jel szórásnégyzetét vizsgáljuk egy spektrumanalizátorral. Megfelelően keskeny frekvenciasávot alkalmazva a mért szórásnégyzet arányos lesz a frekvenciasáv szélességével, és az arányossági tényezőt nevezzük a zaj spektrális sűrűségének:
![\[\left<(\Delta I(t|f_0,\Delta f))^2\right>=S_I(f_0)\Delta f.\]](/images/math/3/3/f/33ff88a562de7a830d972009efd5d850.png)
Megmutatható hogy a zaj spektrális sűrűsége nem más, mint a áram-áram korrelációs függvény Fourier transzformáltjának a kétszerese. A zaj pontos definícióját megismerve a termikus zaj értékét a fluktuáció-disszipáció tétel alapján adhatjuk meg, mely egy rendszer egyensúlyi fluktuációi és az egyensúlyból kitérített rendszer lineáris válaszfüggvénye között teremt összefüggést. Elektromos áram esetén az ez egyensúlyi fluktuáció nem más mint az áramzaj, a lineáris válaszfüggvény pedig a külső feszültségre adott válasz, vagyis a vezetőképesség. Így egy rendszer áramzaja:
![\[S_I(f)=2hf\cdot \coth{\left( \frac{hf}{2k_B T}\right) }\cdot G,\]](/images/math/7/1/3/71389880eece5602647216da934ec1dd.png)
azaz alacsony frekvencián (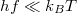
) az áramfluktuációk termikus zaja:
![\[S_I=4k_B TG.\]](/images/math/8/e/b/8eb04ae52b434c6327f7984aa226b808.png)
Hasonlóképpen a feszültségzaj:
![\[S_V=4k_B TR.\]](/images/math/0/0/2/0020cb194bce7954d920a1137e35ea77.png)
Látjuk, hogy a termikus zaj segítségével "csupán" feszültségmérés alapján meghatározhatjuk egy rendszer abszolút hőmérsékletét. Persze a precíz zajmérések komoly méréstechnikai kihívást jelentenek, hiszen nanovoltos vagy még kisebb feszültségek fluktuációját kell pontosan mérni. Ennek ellenére a termikus zaj mérésének komoly metrológiai jelentősége van, hiszen számos módszerrel mérhetünk precízen hőmérsékletváltozást, de az abszolút hőmérsékletet nem könnyű meghatározni. A jelenleg érvényes hőmérsékletstandardok mind ún. másodlagos hőmérők, melyek nem alapvető fizikai törvény hanem megfelelő kalibráció alapján mérik az abszolút hőmérékletet. (A szobahőmérséklet körüli széles tartományban pl. platina vékonyréteg ellenálláshőmérőt használnak standardként.) A termikus zaj mérése alapvető fizikai állandók (Boltzmann állandó + elektron töltés) alapján vezeti vissza a hőmérsékletmérést feszültségmérésre, így a hőmérsékletstandardok kalibrálásának egyik alapvető módszere.
A termikus zaj mellett még két fontos zajtípusról érdemes megemlékezni. Az egyik a szennyezők és rácshibák véletlen mozgásából adódó ún. 1/f zaj, mely alacsony frekvenciákon dominál, és a nevét is a zajsűrűség tipikus frekvenciafüggéséről kapta. A másik az elektrontöltés kvantáltságából adódó ún. sörét zaj, melynek a lényege egy egyszerű példán szemléltethető: Képzeljünk el egy elektronhullámot, mely áthalad egy T transzmissziós valószínűségű nyalábosztón. Az áthaladt töltés értéke T valószínűséggel 1 és 1-T valószínűséggel 0,így az áthaladt töltés T várható értéke körül T(1-T) szórásnégyzetű fluktuációt tapasztalunk. Ezt az elemi folyamatot több elektronra általánosítva megmutatható, hogy a sörétzaj nagysága a rendszerre kapcsolt feszültséggel arányos. A fenti példából érezhető, hogy a sörétzaj kisméretű rendszerekben válik fontossá, ahol egyszerre csak kevés elektron vesz részt a vezetésben.
Mérési feladatok
1. Áramgenerátoros meghajtással vegyük fel a mellékelt párhuzamos LC kör impedanciáját a frekvencia függvényében, határozzuk meg a rezonancia-frekvenciát, a kapacitás az induktivitás ill. az induktivitás soros ellenállásának az értékét. A mért görbét hasonlítsuk össze az elméleti várakozásokkal. A méréshez írjunk számítógépes programot, mely GPIB porton kommunikál a műszerrel. A program adott számú lépésben logaritmikus skálán változtassa a frekvenciát egy megadott kezdő és végfrekvencia között, és vegye fel a bemeneten mért jel X és Y komponensét a frekvencia függvényében. Figyeljünk az időállandó helyes beállítására!
2. Az 1. feladatban készült mérőprogramból kiindulva vegyük fel a mellékelt kvarc oszcillátor rezonancia-görbéjét feszültséggenerátoros meghajtást használva (a rezonancia-frekvencia környékén nagyobb pontossággal!). Ennél a mérésnél a pontosabb frekvenciabeállítás érdekében jelforrásként egy Agilent 33220A függvénygenerátort használjunk. A Lock-In generátorát az Agilent függvénygenerátorhoz szinkronizáljuk, a kvarc oszcillátorra a Lock-In kimenetéről adjuk ki a jelet. Az oszcillátor meghajtásához 1:100 osztót használjunk a Lock-In 5V-os kimeneti jelszintje mellett. Ügyeljünk arra, hogy a rezonancia környékén gerjesztett oszcillátor rezgése nagyon lassan cseng le, így a frekvencia változtatásakor sokat kell várni arra, hogy az új frekvenciához tartozó állandósult állapot kialakuljon.
3. Mérjük meg a mellékelt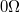 
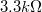-os, 
-os,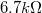 
-os és 
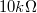-os ellenállások zaját (X noise, Y noise) rögzített, 1kHz és 2kHz közötti frekvenciánál. A mérést hosszú ideig végezzük, és számoljunk időátlagot. Ügyeljünk arra, hogy a kezdeti tranziens szakaszt ne számoljuk bele az időátlagba. Lehetőség szerint a mérést két különböző frekvencián végezzük el. A mért eredmények alapján határozzuk meg a hőmérsékletet és annak hibáját. Az összes mérést ugyan olyan Lock-In beállítás mellett végezzünk, különösen figyeljünk a megfelelő időállandó és méréshatár megválasztására. Használjunk 12dB/Oct ill. Low Noise beállításokat.
 |
| 3. ábra |
 |
| 4. ábra |
Függelék: a méréshez használt eszközök
- SR830 Lock-In + használati utasítás + tápkábel
- Agilent 33220A függvénygenerátor + használati utasítás (elektronikusan) + tápkábel
- GPIB kártya USB csatlakozóval + 1 GPIB kábel
- LC kör fém dobozban
- Kvarc oszcillátor fém dobozban
- Fém doboz ellenállások befogásához termikus zaj méréséhez +
, 
, 
, 
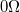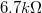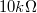-os ellenállások
- Ellenállásdekád
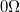-os lezáró
- Kézi multiméter
- Csavarhúzó
- 6db. közepes BNC-BNC kábel
- BNC T-elosztó
- Forrasztó páka
