Tömegmérés rezonanciával és hangsebesség meghatározása
Új mérés! A leírás még készül!
A mérés célja:
- megismerkedni a hangtani mérések alapjaival, valamint a Fourier-transzformációval és annak alkalmazásával
- megismerkedni laboratóriumban használt Vernier LabPro számítógépes adatgyűjtő rendszerrel, és gyakorlatot szerezni a számítógéppel gyűjtött adatok feldolgozásában.
Ennek érdekében:
- áttekintjük egy hangvilla és egy furulya (síp) működési elvét a legegyszerűbb tárgylás szerint
- átismételjük a Fourier-transzformáció alapjait
- méréseket végzünk a számítógépes adatgyűjtő rendszerrel, melynek keretében vizsgáljuk a megszólaltatott hangvilla és a furulya által keltett hangokat és meghatározzuk a levegőbeli fénysebességet
- kiértékeljük az eredményeket IGOR Pro szoftverrel
Tartalomjegyzék |
Elméleti összefoglaló
Bevezetés
A laborgyakorlat során egy hangvilla és egy saját készítésű furulya által keltett hangrezgéseket vizsgáljuk a Vernier LabPro nevű számítógépes adatgyűjtő rendszer és egy mikrofon segítségével.
Mérések hangvillával
A hangvilla egy U alakú, általában acélból készített hangkeltő eszköz, melyet megütéssel szólaltathatunk meg. Sajátos geometriájának köszönhetően az alaphangon kívüli rezgések gyorsan lecsengenek, így 1-2 másodperc után a kívánt stabil rezgést biztosítja, nagyon kevés és gyenge magasabb hang kíséretében. Ezért a tulajdonságáért kedvelt eszköz a zenészek körében a hangszerek behangolásakor.
Az önmagában megszólaltatott hangvilla jellemzően kis hangerővel szól, melyet némiképp befolyásol a megütés ereje, azonban egy megfelelő méretű rezgődobozhoz való csatolással sokkal hatékonyabban növelhetjük a hangerejét. A laborgyakorlaton egy ilyen eszközt fogunk használni, ennek lényege, hogy a félig nyitott fadoboz átveszi a rajta elhelyezkedő hangvilla rezgését, és azt átadja a benne lévő „légoszlopnak”, így felerősítve hallhatjuk a hangvilla rezgése által keltett hangot.
Egy hangvilla alaphangjának kiszámolása a alábbi képlet alapján történhet, ilyenkor fontos ismernünk a villa különböző geometriai paramétereit (l, A), Young-modulusát (E), sűrűségét (
) és másodrendű nyomatékát (I).
![\[ f = \frac{1.875^2}{2\pi l^2} \sqrt\frac{EI}{\rho A}\]](/images/math/e/3/8/e387c055d3f8c743a36709956db5d505.png)
Ezt azonban egyszerűbb módon is elvégezhetjük, ha a csatolt rezgődobozt vizsgáljuk. Azt feltételezve, hogy a doboz a hangvillára van hangolva, a doboz hossza alapján megállapított frekvencia megegyezik a hangvilla frekvenciájával.
Egy ilyen rezgődobozban kialakuló állóhullámokra teljesül, hogy a doboz nyitott végénél duzzadó helyük van, míg a zárt végen csomópont alakul ki. Azaz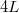 
, 
,
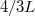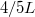, stb. hullámhosszú állóhullámokat várhatunk, melyek közül a 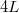hosszú alaphang lesz a hallható a tranziensek gyors elhalása után.
Ezzel a frekvencia egyszerűen kiszámolható a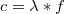 
képlet alapján, ahol 
a hangsebesség levegőben, 
az állóhullám hullámhossza és 
a hang frekvenciája.
Ha megvizsgáljuk a hangvilla frekvenciáját megadó korábbi képletet, négyzet alapú villaágakat feltételezve a másodrendű nyomaték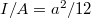 
-nek adódik, ahol 
a négyzet oldalhossza. A Young-moduluszt beírva
a képletet átalakítva azt láthatjuk, hogy megjelenik benne a villa ágainak tömege, mint paraméter.
![\[f = \frac{1.875^2}{2\pi l^2} \frac{a}{l} \sqrt\frac{D}{m}, EZT AT KELL GONDOLNI\]](/images/math/c/5/5/c55ac4962e5652add950ce69c6fed043.png)
Ebből kifolyólag, ha változtatjuk a villa ágainak tömegét, akkor annak elhangolódik a frekvenciája. Ezzel az elvvel a hangvilla tömegmérésre is használható, ha a mérendő tömeget ráhelyezzük a villa egyik ágára, az elhangolja a frekvenciát és ebből meghatározható a tömeg nagysága.
Ennél a leegyszerűsített leírásnál két fontos dolgot kell figyelembe vennünk: egyrészt, a mérendő tömeg anyaga és geometriája eltérő lehet, mint a villa paraméterei, így a fenti képlet nem alkalmazható a frekvencia kiszámolására. Ehelyett egy kalibrációt kell készítenünk, hogy különböző tömegek mennyire hangolják el a villa frekvenciáját. Természetesen az elv akkor működik, amikor az ismeretlen tömeg jóval kisebb, mint a hangvilla tömege.
Másik fontos megjegyzés, hogy a hangvilla előnye, a felharmonikusok gyors lecsengése, főként a nagyon precízen egyformára kialakított villaágaknak köszönhető. Így, amennyiben egy tömeget helyezünk az egyik ágra, ezt a precíz kialakítást elrontjuk. Ezért a mérés során a tömeg rögzítésére használt mágneseket nem csak az egyik ágra helyezzük, hanem mindkettőre, így biztosítva, hogy a villa kialakításának elrontása lehetőleg kicsi legyen.
Mérések furulyával
A gyakorlat egyik feladata egy furulyaszerű hangszer elkészítése és ennek vizsgálata. Az elkészítés pontos menete a Mérési feladatok között olvasható.
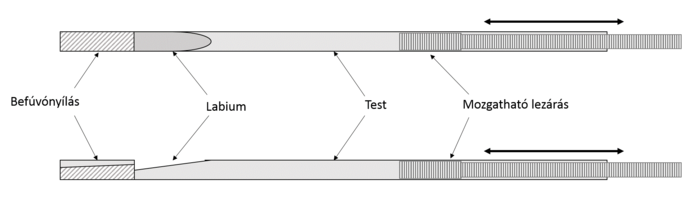
A furulya működésének alapja, hogy a hangszerben egy olyan rezgő légoszlop tud kialakulni, amelynek frekvenciája a kívánt zenei hangot adja. A hangszer felépítése egyszerű, így kevés barkácsolással könnyen elkészíthető. A furulya egy hosszú csőből áll, aminek anyaga jellemzően fa (esetleg műanyag). Ezt a csövet nevezik a furulya testének. A test egyik végén, ahol a hangszerbe a levegőt fújjuk, egy keskeny, a levegő áramlását irányító rés helyezkedik el, majd ezt követi az úgynevezett labium (ajak), ami a hangszer talán legfontosabb része, mivel itt keletkezik a hang.
Amikor a furulyába belefújunk, a beáramló levegő a labiumon „megtörik” és örvények keletkeznek, ezáltal a furulyában lévő légoszlop rezgésbe jön és hang keletkezik. A hang keletkezésének elve hasonló, mint a hangvillánál használt rezgődoboznál, így a furulya alaphangját egyszerűen kiszámolhatjuk annak hosszából. A rezgődoboz egyik vége a labium lesz, itt duzzadó helye van az állóhullámnak, míg a másik vég a furulya vége, ahol szintén egy duzzadó hely lesz. Így a kialakuló állóhullámok rendre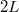 
,
,
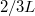hullámhosszúak lesznek, azaz az alaphang hullámhossza .
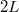Egy furulyával lehetőségünk van különböző hangok keltésére is, mely a testen található megfelelő lyukak lefogásával illetve elengedésével érhető el. Röviden összefoglalva a lyukak szerepe az, hogy rövidítsék a rezgő légoszlop hosszát, mivel ilyenkor nem a furulya végén alakul ki duzzadó hely, hanem a lyuknál, így, mivel a labium és a lyuk közötti távolság rövidebb, magasabb hangon fog szólni a furulya.
A gyakorlat során az egyszerűség kedvéért mi egy kicsit eltérő módon használjuk a furulyát, az egyik végét lezárjuk egy hosszú rúddal, melyet mozgatni tudunk. Így egy félig zárt rezgődobozt hozunk létre, a rúd mozgatásával pedig ennek hossza változtatható, így különböző hullámhosszú rezgéseket vizsgálhatunk majd.
Hangtani mérések elemzése
A fentebb leírt eszközök által keltett hangok vizsgálatához valamilyen módon rögzítenünk kell azokat. Erre a célra egy mikrofont használunk majd, melyet egy XXXX digitális oszcilloszkóphoz csatlakoztatunk. Ez az oszcilloszkóp lehetőséget nyújt a mikrofon jelének, azaz az eszközök hangjának széleskörű vizsgálatára. A beépített mikroszámítógép segítségével maga az oszcilloszkóp képes különféle kiértékelések elvégzésére, az adatok elmentésére (pendrive-ra). A hangtani mérések során ezen funkciók közül a legfontosabb az ún. Fourier-transzformáció lesz.
Egy hangszer által kiadott tiszta hang egy frekvenciájú periodikus jelnek felel meg, melyben az alaphangnak megfelelő frekvenciás szinuszos rezgés mellett az alaphang felharmonikusai is szerepelnek. Ez matematikailag a Fourier-sorfejtés segítségével fogalmazható meg. Vegyünk egy tetszőleges 
frekvenciás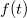 
jelet, melyre:
![\[f ( t ) = f \left( t + \frac{n}{\nu} \right)\]](/images/math/4/6/b/46b352e85fcf713f4b71349858d457c5.png)
tetszőleges 
egész számra. Ez a függvény kifejthető a következő ún. Fourier-sorral:
![\[f ( t ) = \displaystyle\sum\limits_{n=1}^{\infty} A_n \sin \left( 2 \pi n \nu t + \varphi_n \right)\]](/images/math/8/2/c/82c25e4de7b39d06fc5d7bba17bb9060.png)
ahol az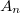 
ill.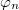 
megadják, hogy a jelben milyen amplitúdóval és milyen fázistolással szerepel az 
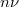frekvenciájú felharmonikus. Azonos hangmagasságon megszólaltatott különböző hangszerek a felharmonikusok eltérő amplitúdói és fázisai miatt szólnak másként.
Ha a jelünk nem periodikus, akkor is felbonthatjuk különböző frekvenciájú komponensekre. Ezt a műveletet hívjuk Fourier-transzformációnak:
![\[F(\nu)=\int\limits_{-\infty}^{\infty} f(t) e^{-{\rm i}2\pi\nu t} {\rm d}t\]](/images/math/e/a/f/eaf1cd1c17b0270a40d9d1d7b9f82dfd.png)
ahol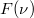 
megadja, hogy egy adott 
frekvenciájú komponens mekkora járulékot ad a jelünkhöz. 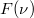komplex szám, melynek abszolút értéke adja meg a frekvenciás komponens amplitúdóját, fázisa pedig a fázistolást. Ha a Fourier-transzformációt egy periodikus jelre alkalmazzuk, akkor az alapfrekvenciánál (), és a felharmonikusoknál (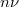) kapunk csúcsokat, melyek nagysága megadja a különböző felharmonikusok amplitúdóját.
Mérésekben a jelünket csak diszkrét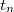 
pontokban ismerjük, így a fenti folytonos Fourier-integrált is ún. diszkrét Fourier-transzformáció (DFT) helyettesíti:
![\[F(\nu)=\displaystyle\sum\limits_{n=1}^{N} f(t_n) e^{-{\rm i}2\pi\nu t_n} \cdot\Delta t_n\]](/images/math/a/3/2/a323933292f99945c358ae14850d1cf7.png)
A diszkrét Fourier-transzformáció hatékony kiszámítására különböző algoritmusokat használhatunk, melyek közül kiemelkedően fontos az ún. FFT, "Fast Fourier Transformation".
A diszkrét Fourier-transzformáció fontos összefüggése a Nyquist-Shannon-féle mintavételezési tétel. Ha egy időfüggő jelből 
idő alatt 
-szer veszünk mintát ekvidisztáns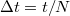 
időközönként, akkor a vett mintából a teljes spektrum csak 
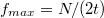maximális frekvenciáig, 
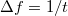feloldással rekonstruálható. Másként kimondva, ha egy 
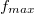frekvenciánál nagyobb frekvenciakomponenst nem tartalmazó (sávkorlátozott) jelet akarunk mintavételezni, akkor legalább 
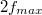mintavételi frekvenciával kell mérni. A mérés hossza pedig a frekvenciafölbontást javítja.
A mérésben egy hangvilla és egy furulyában levő levegőoszlop rezgéseit vizsgáljuk. Ahogy már említettük, a hangvillára jellemző, hogy rezgési spektrumában csak az alaphang szerepel, nincsenek felharmonikusok. Az általunk használt furulyát egy egyik oldalán zárt sípnak tekinthetjük, melyben ideális esetben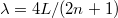 
hullámhosszú állóhullámok alakulhatnak ki, ahol a furulya hossza a labium és a lezárt vég között, pedig egy egész szám. A fenti feltétel abból ered, hogy a labiumnál az állóhullámok duzzadóhelyei, a lezárt végnél pedig csomópontok találhatók. Az így kialakuló rezgések frekvenciái:
![\[\nu=\frac{c}{\lambda}=\frac{c}{4L}(2n+1)\]](/images/math/6/1/5/615d9099d476da67e1e4e27a6a99aedd.png)
ahol a hang terjedési sebessége levegőben. Látszik, hogy félig zárt síp hangjában csak az alaphang páratlan felharmonikusai szerepelnek.
A Vernier LabPro interfész használata
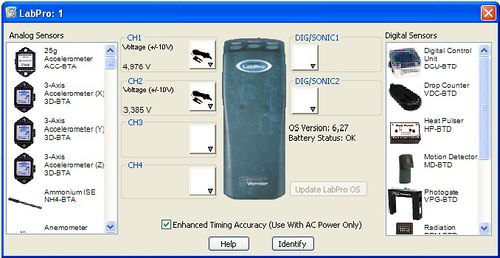
A méréseket a 2. ábrán látható Vernier LabPro interfész segítségével végezzük, melyhez különböző szenzorok csatlakoztathatók. A mérés során két feszültségszenzort ill. egy mikrofont használunk. Az interfész soros vagy USB porton keresztül csatlakoztatható a számítógéphez, és a szenzorok jelét a Logger Pro szoftver segítségével rögzítjük.
A szoftver elindítása után először be kell állítani, hogy milyen szenzorral (szenzorokkal) kívánunk mérni. A 3. ábrán látható ablakhoz az Experiment/Set Up Sensors/ Show All Interfaces gombokkal juthatunk el. Az ábrán látható beállításban az interfész CH1-es és CH2-es bemenetére egy-egy feszültségszenzor van csatlakoztatva.
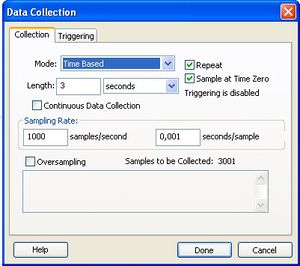
A következő feladat az adatgyűjtés paramétereinek megadása. Az Experiment/Data Collection/Sampling gombokkal a 4. ábrán látható Data Collection ablakhoz jutunk. Itt állíthatjuk be a mérés hosszát és a mintavételezési frekvenciát. (A többi beállítást hagyjuk alapértéken!)
 |
 |
| 3.ábra: A szenzorok beállítása | 4.ábra: Az adatgyűjtés beállítása |
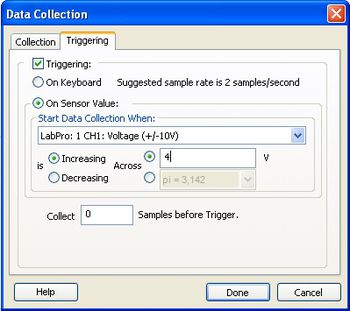
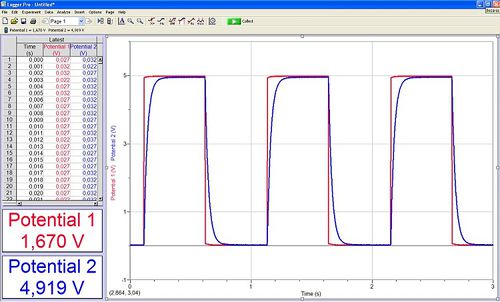
Mindkét mérésnél célszerű a mérőrendszert oszcilloszkóphoz hasonló üzemmódban használni. Ehhez a Data Collection ablakban állítsunk be ismétlődő mintavételezést (repeat), melynek hatására a beállított mérési hossz eltelte után újra kezdi a mérést a rendszer. A mintavételezést a Data Collection ablak Trigger fülében szinkronizálhatjuk a mért jel periódusával. Az 5. ábrán látható beállítás esetén a mintavételezés mindig akkor kezdődik, mikor a mért jel (CH1) értéke pozitív meredekséggel átlépi a beállított 4 V-os küszöbszintet.
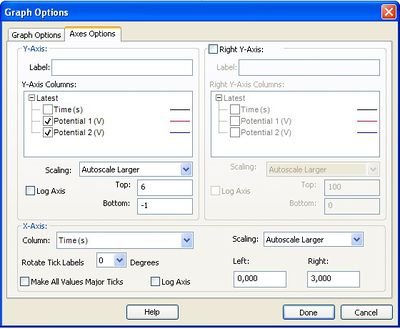
Az Options/Graph Options/Axis Options gombok segítségével jeleníthetjük meg a 6. ábrán látható ablakot, ahol a grafikon tulajdonságait állíthatjuk be.
 |
 |
| 5.ábra: Trigger beállítása | 6.ábra: A grafikon beállítása |
A mérést a fő ablakban (7. ábra) található Collect/Stop gombbal indíthatjuk el, ill. állíthatjuk le.
 |
| 7.ábra: Logger Pro főmenü |
A mérés végén az adatokat nem a Save utasítással kell elmenteni (ekkor olyan fájlt kapnánk, amit később is csak ezzel a programmal tudnánk megnyitni), hanem exportálni kell (File/Export As/Text')! Az így elmentett textfájlokat később bármely más adatkezelő programmal (Igor Pro, Excel, stb.) meg lehet nyitni.
Furulya készítése
A furulya készítésének leírását az Ezermester c. újság 1998-as márciusi kiadásának alapján készítettük, a laborgyakorlatnak megfelelően átírva. Az eredeti leírás ezen a linken olvasható.
 |
| xxxxx.ábra: Furulya sematikus vázlata |
- A furulya testének kiválasztása
- A korábbi képletek alapján számolja ki, hogy milyen hosszúságú furulyatestet kell használnia a xxxHz-es alaphang megszólaltatásához. Vegye figyelembe, hogy a test hossza 4-5 cm nagyobb kell legyen, mint a valós rezgőcső hossza.
- Vágjon le egy megfelelő hosszúságú darabot a műanyagcsőből!
- A labium kialakítása
- Ez a furulyakészítés legnehezebb művelete, mivel a megfelelően kialakított ajak a kulcsa a tiszta hang keltésének.
- A cső egyik végétől mérjünk le 2 cm-t, majd egy szikével merőlegesen vágjuk be a csövet kb 5mm-nyire. Ettől a vágástól mérjünk le további 1 cm-t (azaz a végtől 3cm-t), majd innen a korábbi bevágásig ferdén vágjuk be a csövet, ezzel egy ék alakot kiformázva. Érdemes először kisebb meredekségű bevágást ejteni és utána korrigálni, nehogy túl mély éket alakítsunk ki.
- Labium formázása
- Az előző lépésben készített ékalak éle egyenetlen lesz, ami rontja a furulya hangjának minőségét, nehéz lesz megszólaltatni és levegősen fog szólni. Ezen javíthatunk, ha egy reszelővel eldolgozzuk a vágáskor kialakult sorját, valamint az ékalakot szabályosra formázzuk. A reszelővel óvatosan dolgozzunk, mert túlreszelve elrontható az eddigi munkánk.
- Befúvónyílás kialakítása
- A furulya ék felőli végén ki kell alakítanunk egy, a test belső átmérőjéhez képest keskeny, nyílást, ez lesz a befúvónyílás. Ehhez vágjunk le egy kb. 2 cm hosszú darabor a farúdból, a pontos méretet az ék kezdete és a test végének megfelelően mérjük le. Ebből a fadarabból egy szike segítségével hasítsunk le egy darabot, enyhén átlósan, azaz egyik végén kicsit több anyagot szedjünk le. Ezt is érdemes kisebb lépésekben végezni, különösen ügyelve a balesetek elkerülésére!
- Amint elkészül a kívánt alak, helyezzük bele a furulya végébe. Ha nem szorul a fadarab a furulya testében, szigetelőszalaggal körbetekerve növelhetjük a vastagságot.
- Lezáró rúd elkészítése
- Az előző lépések végén a furulya az alaphangon megszólaltatható, ha a végét kezünkkel befogjuk. Más hangok keltéséhez azonban lyukak kialakítása helyett a furulya testének hosszát fogjuk változtatni. Ehhez egy olyan lezárást készítünk, aminek pozíciója változtatható a furulya testében.
- A rendelkezésre álló farúdból mérjen le egy akkora darabot, ami elég hosszú, hogy a furulyában elérjen a labiumig, valamint ilyen, teljesen betolt pozícióban is lógjon ki elegendő rész a mozgatáshoz.
- A rúd egyik végét tekerje be szigetelőszalaggal, úgy, hogy lezárja a furulya testét, de könnyen mozgatható legyen benne. Itt is érdemes több lépésben dolgozni, ne legyen túl vastag a szigetelőszalag réteg. Végül kenje be a szigetelőszalagot vákuumzsírral, ezzel elősegítve a könnyebb mozgatást és a jobb tömítettséget.
Ezzel a saját készítésű furulya elkészült, amennyiben a labium kialakítása megfelelő, könnyen megszólaltatható és különböző hullámhosszú hangok kelthetők.
Mérési feladatok
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
Hangvilla vizsgálata
1. Mérje meg a hangvilla frekvenciáját az oszcilloszkóp segítségével! Állítson be egy megfelelő mintavételezési időt úgy, hogy a képernyőn legalább 10 periódus látszódjon. Üsse meg a hangvillát, majd a tranziensek elhalása után, amikor az oszcilloszkópon szabályos szinuszos jelalak látható, állítsa le a mérést.
- Az oszcilloszkóp megfelelő beállításához számolja ki a hangvilla frekvenciáját kétféle módon (hangvilla paraméterei, rezgődoboz mérete)! A kapott értékeket vesse össze! Melyik módszerrel számolt frekvenciának nagyobb a hibája?
- A méréshez egy oszcilloszkópra kötött mikrofont használunk. Hova célszerű helyezni a mikrofont a méréskor?
2. Határozza meg a hangvilla frekvenciáját gyors Fourier-transzformációval (FFT)! Ehhez állítsa az oszcilloszkópot FFT módba és válasszon megfelelő időalapot, valamint FFT ablakot.
- Mi alapján határozza meg az optimális időalapot? Milyen frekvencia felbontással tud így mérni? Miért fontos a mérésnek megfelelő FFT ablak kiválasztása?
- Próbáljon ki több FFT ablakot és időalapot, majd írja le tapasztalatait!
3. Vizsgálja meg, milyen mértékben rontja el a hangvilla tulajdonságait a paramétereinek változtatása! Először helyezzen egy mágnest az egyik ágra és vizsgálja a felharmonikusok megjelenését. Ezután helyezzen egy ugyanilyen mágnest a másik ágra, minél pontosabban a másik mágnessel megegyező helyre. Szintén vizsgálja meg a felharmonikusok megjelenését, valamint minél pontosabban határozza meg az így kialakított hangvilla frekvenciáját. Határozza meg a mágnesek tömegét a frekvencia eltolódásából!
- Milyen irányú frekvenciaeltolódást vár a mágnesek felhelyezésekor? Becsülje meg ennek mértékét! (mágnes mérete, tömege, villa tömege, paraméterei, stb. becslése)
- Ha azzal a feltételezéssel élünk, hogy a felhelyezett mágnesek csak a villa tömegét módosítják, a frekvencia eltolódásából meghatározható a mágnesek tömege. Fejezze ki a mágnesek tömegét a mért frekvenciákkal!
4. Mérje meg különböző ismert tömegek esetén a frekvencia eltolódást és készítsen kalibrációs görbét, ami alapján egy ismeretlen tömeg által okozott frekvencia eltolódásból meghatározható a tömeg mértéke! Határozza meg, milyen felbontással tud ezzel a módszerrel tömeget mérni!
- Az előző feladatban azt feltételeztük, hogy a villára helyezett tömeg egyszerűen csak a villa tömegét módosítja. A fenti képleteket áttekintve látható, hogy ez egy jó közelítés, de pontos méréshez nem lesz megfelelő. Mivel egy így kialakított rendszer esetén a számítások bonyolultak, nem a képletek alapján célszerű számolni, hanem inkább ismert tömegekkel kalibrálni az eszközt.
- Gondolja át a mérés lehetséges hibáit, ezeket jegyezze le a mérési naplóba is!
5. Határozza meg két ismeretlen tömeg mértékét minél pontosabban!
