Kaotikus kettős inga vizsgálata V-scope-pal
A mérés célja:
- megismerkedni egy kaotikus rendszerrel,
- tanulmányozni a mozgás kaotikussá válását.
Ennek érdekében:
- röviden bemutatjuk a kaotikus kettős ingát,
- mérjük a kaotikus kettős inga mozgását V-scope segítségével,
- kiértékeljük a mérési eredményeket.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
A kaotikus kettős inga
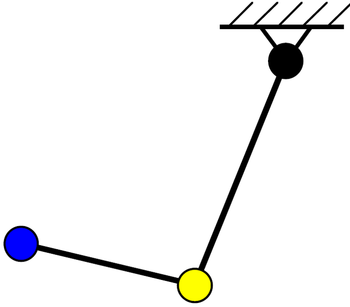
Kettős ingát úgy készíthetünk, hogy egy inga végéhez csuklóval egy másik ingát erősítünk (1. ábra). Ez a rendszer, egyszerűsége ellenére, kaotikusan viselkedik.
A káosz fogalma
A kaotikus rendszer viselkedése hosszútávon megjósolhatatlan. Ennek oka a kezdőfeltételekre való rendkívüli érzékenység: ha a rendszert a legcsekélyebb mértékben különböző kezdeti feltételekkel hagyjuk magára, akkor véges időn belül teljesen eltérően fog viselkedni. Ugyanakkor pontosan ugyanazt a kezdőállapotot – ha másért nem, a Heisenberg-féle határozatlansági reláció miatt – soha nem tudjuk megvalósítani.
Mikor lehet egy rendszer kaotikus? Ha a rendszernek legalább három szabad paramétere van és a rendszert leíró differenciál-egyenletek nemlineáris tagot is tartalmaznak. A három szabad paraméter azért szükséges, mert ekkor a fázistérben kialakulhat olyan trajektória, amely nem konvergál sem egy véges ponthoz, sem a végtelenbe, és ugyanakkor soha nem záródik. Két dimenzióban ez nem lehetséges (2. ábra).
A kettős inga, mint kaotikus rendszer
A kettős inga egy állapotát legegyszerűbben a két kar szöghelyzetével és szögsebességével adhatjuk meg. Ez összesen négy paraméter, de – konzervatív rendszer esetében – az energia-megmaradás miatt a négyből csak három paraméter változhat függetlenül. A rendszer differenciál-egyenletei könnyen felírhatóak és adott kezdeti feltételek mellett numerikus módszerekkel megoldhatóak. Numerikus modellezésnél, a valódi kísérletektől eltérően, természetesen megtehető, hogy pontosan ugyanabból az állapotból indítjuk el a rendszert - és ekkor a megoldás is ugyanaz lesz.
A mérési gyakorlaton azt vizsgáljuk, hogy különböző indítási helyzetek (azaz különböző kezdeti energiák) esetében mennyire érzékeny a rendszer a kezdőfeltételekre. Ehhez a kettős ingát a lehető legpontosabban ugyanabból a helyzetből többször egymásután el kell indítani, és az egyes mozgásokat össze kell hasonlítani. Az összehasonlítás sokféle paraméter szerint lehetséges, de a különbségek akkor a leglátványosabbak, ha az egyes karok forgásszögét ábrázoljuk az idő függvényében.
A V-scope mérőberendezés
A V-scope mérőberendezés és a Vscope for Windows szoftver részletes leírása a Csatolt ingák mérése V-scope-pal című fejezetben található.
A mérési elrendezés
A gyakorlaton vizsgált kettős inga golyós csapágyakkal egymáshoz, illetve egy stabil állványhoz erősített fa lapokból áll (tehát az 1. ábrán látható rajztól eltérően kettős fizikai inga). A golyóscsapágyaknak köszönhetően a rendszer csillapítása kicsi (de természetesen nem nulla). Az energiaveszteség csökkentése érdekében fontos az állvány minél stabilabb rögzítése (ólom és beton nehezékekkel).
A mozgás vizsgálatakor a rögzített tengelyű, hosszú ingakar (továbbiakban nagy kar) rögzített végét választjuk a koordinátarendszer origójának. A két kart összekapcsoló tengelyhez rögzíthetjük a V-scope sárga, míg a rövidebb ingakar (továbbiakban kis kar) végéhez a kék gombocskát. A V-scope tornyait a kettős ingától kb. 3 m távolságra, az ingák lengéssíkjával párhuzamosan állítjuk fel. A méréshez használható "sablon"-ban a vízszintes tengelyt  -nek, a függőleges tengelyt
-nek, a függőleges tengelyt  -nak definiáltuk.
-nak definiáltuk.
Mérési feladatok
1. Ellenőrizze, hogy a V-scope tornyai megfelelően vannak-e csatlakoztatva a mikroszámítógéphez, illetve a mikroszámítógép a PC-hez! Kapcsolja be a mikroszámítógépet és a PC-t, majd indítsa el a V-scope for Windows szoftvert! A "Sablonok" mappában nyissa meg a méréshez előkészített, de adatokat nem tartalmazó kaotikus.vsw fájlt ("sablon"-t)! A Csatolt ingák mérése V-scope-pal jegyzet 1.5 részében leírtak szerint állítsa be az origót a nagy ingakar tengelyéhez. (A mérőpár egyik tagja tartsa ott valamelyik gombocskát a beállítás alatt!) Rögzítse a sárga gombocskát a nagy, a kék gombocskát a kis ingakar végén lévő tartóba, majd ellenőrizze a Csatolt ingák mérése V-scope-pal jegyzet 1.4 részében leírt beállításokat!
2. A nagy kar végén lévő cérna segítségével térítse ki a nagy kart körülbelül 5°-kal a függőlegeshez képest! A kis kart hagyja szabadon, függőleges helyzetben lógni! A piros "Record New Data" gombra való kattintással indítsa el a V-scope-ot és a "műszerek"-en olvassa le és jegyezze fel a sárga gombocska x és y koordinátáját! Ha az értékek már nem változnak, engedje el a cérnát! (Vigyázzon arra, hogy az indításkor ne rántsa meg a cérnát, az inga ne kapjon kezdősebességet!) A mérés befejeztével mentse el a fájlt új néven a "D/Vscope/Meresek" mappába!
Ezután a piros "Record New Data" gombra való kattintással indítsa el újra a V-scope-ot, és a "műszerek" segítségével állítsa be a lehető legnagyobb pontossággal az előző indítási helyzetet! Győződjön meg róla, hogy mindkét inga nyugalomban van és engedje el a cérnát! A mérés befejeztével mentse el a fájlt új néven!
Ismételje meg még kétszer a mérést! (Tehát ugyanabból az indítási helyzetből összesen 4 mérést végezzen!)
3. Ismételje meg a 2. pontban leírtakat a nagy ingakar 30, 60, 90, 120, 150 és 175°-os kitérítésével! Mindegyik esetben négy-négy mérést végezzen!
4. Nyissa meg a Vscope for Windows szoftver segítségével egyenként a fájlokat! A visszajátszó gombok (Csatolt ingák mérése V-scope-pal jegyzet 1.5 része, 1. táblázat) segítségével keresse meg azt a pillanatot, amikor a mozgás elindul! Az "óráról" (az időt mutató "műszerről") olvassa le az ehhez a pillanathoz tartozó 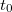 időt!
Az Edit/Trim Data parancs hatására megjelenő "Trim Data" ablakban (Csatolt ingák mérése V-scope-pal jegyzet 1.7 része) vágja le a
időt!
Az Edit/Trim Data parancs hatására megjelenő "Trim Data" ablakban (Csatolt ingák mérése V-scope-pal jegyzet 1.7 része) vágja le a 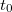 időpont előtti adatokat! Ezáltal a mozgás kezdőpillanata
időpont előtti adatokat! Ezáltal a mozgás kezdőpillanata  lesz. Ehhez hasonlóan vágja le a
lesz. Ehhez hasonlóan vágja le a 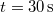 utáni adatokat! Így a továbbiakban egyforma hosszúságú adatsorokkal lehet dolgozni. Ezután mentse el a módosított fájlt! A Save Table paranccsal kapcsolatos problémák miatt (Csatolt ingák mérése V-scope-pal jegyzet 1.6 része) az adatok textfájlba való kiolvasásához használja a kiolvaso.exe programot!
utáni adatokat! Így a továbbiakban egyforma hosszúságú adatsorokkal lehet dolgozni. Ezután mentse el a módosított fájlt! A Save Table paranccsal kapcsolatos problémák miatt (Csatolt ingák mérése V-scope-pal jegyzet 1.6 része) az adatok textfájlba való kiolvasásához használja a kiolvaso.exe programot!
Az adatok további kiértékelése szabadon választható programmal (pl. Excel táblázatkezelő, Pascal, Basic, gnuplot, stb.) végezhető.
5. A V-scope a gombocskákat nem egy időben, hanem felváltva méri (először a sárga, majd a kék gombocskát). Így a kék gombocska relatív helyzetének pontosabb kiszámításához a sárga gombocska koordinátáihoz tartozó időadatokat a mintavételezési periódussal csökkenteni kell, és a kék gombocska koordinátáihoz tartozó időpontokhoz interpolációval kell meghatározni a sárga gombocska koordinátáit. Ezután a sárga és a kék gombocska  és
és  koordinátáiból határozza meg a kék gombocska sárga gombocskához viszonyított
koordinátáiból határozza meg a kék gombocska sárga gombocskához viszonyított 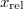 és
és 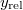 relatív koordinátáit!
relatív koordinátáit!
6. A sárga gombocska  és
és  , illetve a kék gombocska
, illetve a kék gombocska 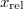 és
és 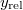 koordinátáiból határozza meg a nagy és a kis kar forgásszögét az idő függvényében! Figyeljen arra, hogy a kis kar többször is körbefordulhat, ezért a szög
koordinátáiból határozza meg a nagy és a kis kar forgásszögét az idő függvényében! Figyeljen arra, hogy a kis kar többször is körbefordulhat, ezért a szög 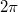 -nél nagyobb, illetve negatív is lehet!
(Egy lehetséges módszer a gombocskák sebességének, majd a karok előjeles szögsebességének meghatározása, majd ennek a függvénynek idő szerinti numerikus integrálása. Természetesen más módszert is választhat.)
-nél nagyobb, illetve negatív is lehet!
(Egy lehetséges módszer a gombocskák sebességének, majd a karok előjeles szögsebességének meghatározása, majd ennek a függvénynek idő szerinti numerikus integrálása. Természetesen más módszert is választhat.)
7. Ábrázolja (külön-külön) a nagy és a kis kar forgásszögét az idő függvényében! Az ugyanonnan elindított mérések eredményeit ugyanabban a grafikonban ábrázolja! Vizsgálja meg, hogy különböző indítási helyzetek esetében mennyi ideig "reprodukálódik" a mozgás és mikor válik kaotikussá! Eredményeit foglalja táblázatba és értékelje!