Mérések oszcilloszkóppal: hangsebesség és fénysebesség vizsgálata
A mérés célja:
- megismerkedni az elektronikai méréstechnikában leggyakrabban használt készülék, az oszcilloszkóp működésével és használatával,
- különböző mérések megismerése, kezdve az egyszerű jelalakok vizsgálatától a hangsebesség megméréséig
- egy ötletes módszer megismerése, mellyel a fény sebessége meghatározható ill. nagyfrekvenciás jelek mérhető tartományba transzformálhatók,
Ennek érdekében:
- megismerkedünk az oszcilloszkóp felépítésével és kezelőszerveivel,
- megvizsgáljuk néhány jelalak fontosabb jellemzőit,
- néhány egyszerű áramkörben megvizsgáljuk a fellépő feszültségek fázisviszonyait,
- megmérjük a hangsebességet egy hangszóró és egy oszcilloszkópra kötött mikrofon segítségével
- összeállítunk és kalibrál egy a fénysebesség mérésére akár laboratóriumi körülmények között is alkalmas rendszert
- meghatározzuk a fény sebességét levegőben, szerves üvegben, ill. vízben.
Tartalomjegyzék |
=Az oszcilloszkóp bemutatása
Az oszcilloszkóp az elektronikai méréstechnika leggyakrabban használt, legsokoldalúbb készüléke. Közvetlenül feszültség–idő függvényt vagy fázishelyzetet jelenít meg a képernyőjén. Ez a megjelenítő képesség az, ami lényegesen több információ megszerzését teszi lehetővé, mint amennyi például multiméterrel lehetséges.
Oszcilloszkóppal az alábbi mennyiségek mérhetők közvetlen vagy közvetett módon:
- egyenfeszültség,
- váltakozó feszültség,
- egyenáram,
- váltakozó áram,
- idő, időkülönbség,
- fázis, fáziskülönbség,
- frekvencia.
Oszcilloszkópos vizsgálattal észrevehető a jelalak torzulása, mérhető a jel egyen- és váltóáramú komponense, gerjedés, felharmonikusok jelenléte látható. Többcsatornás készülékkel lehetséges több, általában kettő vagy négy időfüggvény egyidejű vizsgálata és összehasonlítása.
Az oszcilloszkóp felépítése és működése=
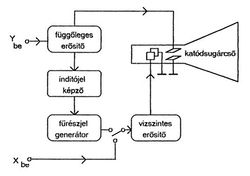
Az oszcilloszkóp fő részeit és kapcsolódásukat az 1. ábra mutatja.
Katódsugárcső
A katódsugárcső az oszcilloszkóppal vizsgált jelalakok megjelenítését végzi megfelelő vezérlés esetén. A katódsugárcső kúpos kialakítású, tölcsérszerű zárt vákuumcső. Vékony, hengeres részében van az elektronágyú. A fűtött katódból az anód és katód közötti elektromos tér hatására kilépnek az elektronok és az anód felé gyorsulnak. Ha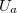 
az anód és katód közötti potenciálkülönbség, 
a katód-anód távolság, az 
tömegű,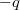 
töltésű elektronra az így kialakuló 
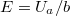nagyságú térerősség 
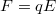erővel hat az anód irányába. A munkatételt alkalmazva írhatjuk, hogy 
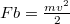, ebből az elektronok sebessége az anódnál kifejezhető: 
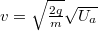. (Feltételeztük, hogy a katódból kilépő elektronok sebessége elhanyagolható.)
Az anódon levő résen áthaladó elektronokat egy fókuszáló rendszer nyalábbá formálja. A sugár vízszintes és függőleges irányú eltérítését síkkondenzátor-szerű, egymással 90°-os szöget bezáró párhuzamos lemezpárok közötti elektromos tér végzi. A cső kiszélesedő végét lezáró oldal belső felülete fluoreszkáló anyaggal van bevonva. A képernyőre elegendően nagy sebességgel becsapódó elektronok rövid idejű felvillanást okoznak.
A cső geometriai és elektromos paraméterei nagymértékben meghatározzák az egész készülék használhatóságát.
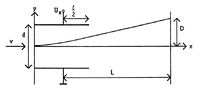
A függőlegesen eltérítő lemezekre feszültséget kapcsolva a lemezek között kialakuló elektromos tér (
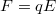) nagyságú erővel hat a 
kezdősebességgel a lemezek közé érkező 
töltésű elektronokra (2. ábra).
Ennek hatására az elektronok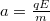 
gyorsulással mozognak függőleges irányba.
Vízszintes irányú sebességük változatlan, ezért a befutott pálya a lemezek között parabola lesz (vízszintes hajítás).
![\[ x=vt , \]](/images/math/2/e/b/2eb48b7349bd51ddd25f62382abe2f41.png) |
![\[ y=\frac{a}{2}t^2, \]](/images/math/a/1/1/a11282c635686c378574e0898d680395.png) |
![\[ y=\frac{qE}{2mv^2}x^2 \]](/images/math/8/1/a/81a10952f014738f01375e63b4fed995.png) |
Az elektronok a lemezeket elhagyva a pálya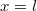 
pontbeli érintője mentén állandó sebességgel haladnak tovább. A lemezek középpontjától 
távolságban levő képernyőt 
magasságban érik el. A pálya iránytangense a lemezek szélénél:
![\[\tan\alpha = \frac{qEl}{mv^2}\]](/images/math/b/c/7/bc787f78ad12f16c911c3945f6cb2f7c.png)
az egyenes egyenlete:
![\[y=\frac{qEl}{mv^2}(x-\frac{l}{2})\]](/images/math/1/f/8/1f85633d7535c3f236d0e7a24f46b10d.png)
Az eltérítés mértéke az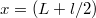 
helyen:
![\[D = \frac{qE}{mv^2}lL\]](/images/math/f/4/2/f42d7c263164d05b51fd627faff8fd74.png)
A lemezek közötti térerősség a rájuk kapcsolt eltérítő feszültségből származik:
![\[E=\frac{U_e}{d}\]](/images/math/9/3/2/9327086ea23a19d8a5a9ac471cb1ff8f.png)
Ezeket felhasználva az eltérítésre a következő összefüggés adódik:
![\[D = \frac{lL}{2dU_a}U_e\]](/images/math/e/0/9/e09b56c53df21ac03aaa38379fe7f996.png)
A katódsugárcső érzékenységét az egységnyi eltérítő feszültség hatására létrejövő eltérüléssel definiáljuk:
![\[\frac{D}{U_e}=\frac{lL}{2dU_a}\]](/images/math/e/5/1/e51207a49654195de30b91560aba53ec.png)
Fűrészjel generátor
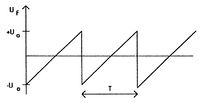
Az oszcilloszkóppal leggyakrabban periodikus időfüggvényeket vizsgálunk, vagyis a képernyő vízszintes tengelye az időtengely. Mivel a jelek időben nagyon gyorsan változnak, a bejövő jel egy darabjának egyszerű felrajzolását szemmel nem tudjuk értékelni és nem lehet kiértékelni, ezért biztosítani kell a folyamatos, azonos pozíciójú ábrázolást. A fűrészjel generátor a 3. ábrán látható jelet állítja elő, amely a vízszintes erősítőn keresztül a vízszintesen eltérítő lemezpárra jut. A felerősített jel akkora, hogy az elektronnyalábot a képernyő szélső pontjáig kitéríti.
A jel periódusideje változtatható, ez az idő lesz a vízszintes tengely "hossza", ennyi idő alatt fut végig az elektronnyaláb a képernyőn. A periódusidő minél tágabb határok között változtatható, annál gyorsabb jelek vizsgálatára van mód, mert akkor kapunk jól kiértékelhető ábrát, ha a bejövő jel változási sebessége (függőleges eltérítés) és vízszintes eltérítés sebessége azonos nagyságrendű. (Másként fogalmazva: a fűrészjel periódusideje közel egyenlő legyen a bejövő jel néhány periódusával.)
Indító jel képző (szinkronizáló)
A szinkronizáló egység feladata, hogy a gyorsan változó bejövő jeleket azonos kezdőfázissal kezdje kirajzolni a képernyőre. A 4. ábrán látható szinusz-jel érkezik az 
bemenetre. A 0 időpontban a fűrészjel generátor feszültségének értéke legyen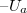 
, vagyis az elektronsugár a képernyő bal szélén van. Ha 
a fűrészfeszültség periódusideje, akkor az ábrán vastagon megrajzolt görbedarabot fogjuk látni a képernyőn. Amikor a nyaláb visszafut a képernyő bal szélére, irányú kitérés nem egyezik meg az előző induláskor felvett értékkel. Ezért, ha most azonnal kezdődne a következő vízszintes kitérítés (indulna a fűrészjel-feszültség második periódusa), akkor a képernyőn az előzőhöz képest egy másik görbedarabot rajzolna fel. Ezt így folytatva könnyen belátható, hogy a különböző szinusz-darabok halmaza miatt egy világító sávot látnánk kiértékelhető jel helyett. A szinkronizáló egység feladata, hogy a fűrészjel generátor következő periódusát a bejövő jel egy beállítható értéke elérése esetén engedi csak elindulni. Ez azt jelenti, hogy az Y bemenetre adott jel hosszúságú, azonos kezdőfázisú szakaszait rajzolja egymásra. A jel ábrán besatírozott, vékonyított részeit nem fogjuk látni, de ez nem okoz információ veszteséget, mert ha -t úgy választjuk meg, hogy az nagyobb, mint a bejövő jel periódusa, akkor a jelről minden információ leolvasható.
Vízszintes és függőleges erősítő
A katódsugárcső paramétereiből adódik, hogy mekkora feszültség szükséges az elektronsugár kitérítéséhez a képernyő széléig. (Általában néhány száz volt.) A vizsgált jelek nagysága széles tartományban változhat, az erősítés állításával lehet az optimális feszültséget beállítani úgy, hogy az ábra kitöltse a képernyőt. A vízszintes erősítő vagy a fűrészjel generátor jelét vagy az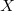 
bemenetre adott külső jelet erősíti.
A kétcsatornás oszcilloszkóp
A gyakorlatban sokszor előfordul, hogy egyszerre több (kettő) időfüggvényt kellene vizsgálni. Ez úgy oldható meg, hogy a függőleges eltérítő lemezekre felváltva kapcsolják a két bejövő jelet, vagyis egy időben két időfüggvény látható. Lassú jelek esetén egy-egy rövid darabkát felváltva rajzol fel az elektronnyaláb mindkét jelből (chopper üzemmód). Gyors jeleknél a fűrészjel generátor egyik periódusában az egyik, következő periódusában a másik jelet ábrázolja (alternatív üzemmód).
Digitális oszcilloszkóp
Egyszerű mérések oszcilloszkóppal
Periodikus feszültség vizsgálata
A vizsgált jelet (feszültség-idő függvény) az Y bemenetre kapcsolva, és a belső vízszintes eltérítést használva vizsgálhatjuk a jeleket. Megadható a jelalak, amplitúdó, periódusidő, frekvencia.
Egymásra merőleges harmonikus rezgések összetétele
Két egyenlő frekvencia fázisszögének mérése
Ebben az esetben a fűrészjel generátort kikapcsoljuk és a vízszintes eltérítést az X bemenetre adott jel végzi. Ha az X bemenetre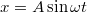 
jelet, az Y bemenetre 
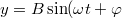) jelet kapcsolunk, egyszerű helyettesítéssel adódik, hogy
![\[y = \frac{Bx}{A}\cos\varphi+B\sqrt{1-\frac{x^2}{A^2}}\sin\varphi\]](/images/math/f/8/a/f8a5590f45772e816f745f11e96b0848.png)
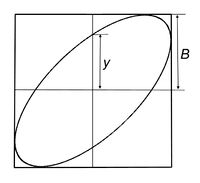
A kapott egyenlet egy ellipszist ír le. A fázisszög az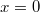 
-nál leolvasott érték és 
ismeretében számítható (5. ábra):
![\[\varphi = \arcsin\frac{y}{B}\]](/images/math/8/f/a/8faaffaa443221462fc29585545b0025.png)
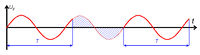
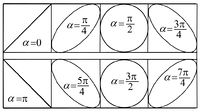
Néhány, különböző fázisszöghöz tartozó jelalakot mutat a 6. ábra 
esetén.
Különböző frekvenciájú rezgések vizsgálata
Ha a rezgések frekvenciái kicsit különböznek, a képernyőn ez úgy jelenik meg, mint azonos frekvenciájú rezgések közötti lassú, folyamatos fázisváltozás. A görbe végighalad a 6. ábrán látható helyzeteken, lebegés jön létre.
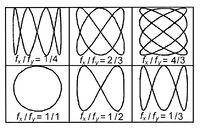
Ha a frekvenciák jelentősen különböznek, lényegesen bonyolultabb ábrák alakulnak ki, Lissajous-görbék keletkeznek. Ha a frekvenciák aránya racionális, akkor önmagába záródik a görbe (7. ábra), ha nem, akkor a képernyőt teljesen behálózó, nem záródó ábrát kapunk. A frekvenciák arányát a következő módon lehet meghatározni:
![\[\frac{f_x}{f_y} = \frac{N_y}{N_x}\]](/images/math/d/1/e/d1ea0ce704add0ac6378ca94bea788ce.png)
ahol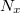 
és 
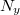a vízszintes és függőleges oldalak érintési pontjainak száma.
Hangsebesség mérése
Hang illetve longitudinális hullám terjedési sebességének mérése alapján hasznos információkat kaphatunk a közeg összetételéről, állapotáról. A számtalan mérési módszer közül az egyik legegyszerűbbet használjuk. Visszavezetjük a mérést fáziskülönbség és távolság mérésére.
Hangsebesség mérése levegőben
A hangforrás legyen egy hangszóró, amit szinuszos jellel vezérlünk. A vevő egy mikrofon, amely mozgathatóan van elhelyezve. A vezérlő jel és a mikrofon jele egy oszcilloszkóp X és Y bemenetére kerül. Adott hullámhosszúságú vezérlő jel esetén a hangszóró és a mikrofon távolsága kifejezhető:
![\[d = k\lambda + b\lambda\]](/images/math/0/e/b/0eb21f83d64ab1af2d3bd3741b8f0b57.png)
ahol 
egész szám, pedig egynél kisebb. Az oszcilloszkópon tehát egy ferde tengelyű ellipszist fogunk látni. Beállíthatjuk úgy a mikrofont, hogy nulla legyen, vagyis egy egyenest kapjunk a képernyőn. Ha most a mikrofont lassan mozgatjuk, pl. a hangszóró felé, akkor az ismert ellipszisek alakulnak ki, majd az eredetihez képest 90°-kal elfordult egyeneshez jutunk. Ekkor a mikrofon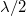 
távolsággal mozdult el. A frekvencia ismeretében a sebesség számítható:
![\[c=\lambda \nu\]](/images/math/5/e/6/5e695f4e6385c1415b899df8a3ae2f11.png)
Fénysebesség mérése
A vákuumra vonatkozó fénysebesség az egyik fontos természeti állandó, melynek meghatározása alapvető szerepet játszott a modern fizikai világkép kialakításában. Az a felismerés, hogy az elektromágneses sugárzás véges sebességgel terjed, alapjaiban rendítette meg a távolhatáson alapuló (a kölcsönhatások végtelen sebességgel való terjedését feltételező) korábbi világképet. A fénysebesség az elektromágnesség Maxwell által kidolgozott általános elméletében, a speciális és általános relativitáselméletben, és a kvantum-térelméletben lépten-nyomon előforduló mennyiség.
Azt, hogy a fény haladási sebessége véges, először Olaf Römer dán csillagász mutatta ki 1676-ban a Jupiter egyik holdja keringési idejének változása alapján. Az általa becsült érték 
= 225 000 km/s még lényegesen eltér a ma definíciószerűen rögzített 299 792 458 m/s értéktől. (Manapság a lézeres méréstechnika segítségével a fénysebesség nagy pontossággal mérhető. Ezért 1983 óta a távolság egységét a fénysebesség segítségével definiálják: 1 m az a távolság, amit a fény vákuumban 1/299 792 458 s alatt befut.) A fénysebesség meghatározására számos módszert dolgoztak ki, mint pl. a Foucault által javasolt és Michelson által tökéletesített forgó tükrös eljárás, melynek hibája kb. 5 %. A jelen gyakorlat során egy ötletes, a modern elektronika lehetőségeit kihasználó módszerrel ismerkedünk meg, mely valamivel pontosabb, mint a forgótükrös eljárás (hibája kb. 1 %).
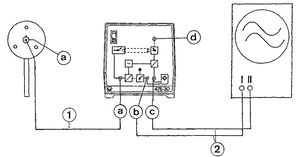
A mérési módszer elvének bemutatása
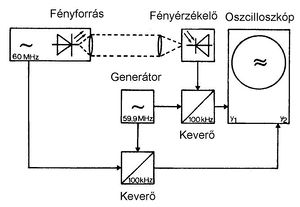
A fénysebesség meghatározásánál csak akkor nincs szükség nagy távolságokra, ha igen rövid időket tudunk mérni. A jelen mérésben alkalmazott távolságok nagyságrendje ~ 1 m. A fellépő igen rövid idők (~ ns) mérését az alábbi megoldás teszi lehetővé: Egy olyan LED fényét vizsgáljuk, mely 60 MHz-el villog. (A mérőeszköz blokk-diagramja az 1. ábrán látható.) A fényforrást és az érzékelő egységet (mely a fotodiódát, erősítőt, jelkeverőket és a tápegységet tartalmazza) egy 6 m-es koaxiális kábel köti össze. Ez a kábel továbbítja a fényforrás elektronikája által előállított 60 MHz-es jelet az elektronikai dobozban található keverő egységbe és biztosítja a fényforrás tápfeszültségét. A fényforrás (fotodióda) által kibocsátott fényt, a forrás és az érzékelő közti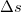 
út megtétele után, az érzékelő fotodióda 60 MHz-es váltófeszültséggé alakítja, melynek fázisa az eredeti jelhez képest a 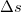úttal arányos 
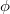fázisszöggel (
időtolással) késik. Ekkor a fény sebessége
![\[c = \Delta s / \Delta t\]](/images/math/0/1/9/0199aa9c4d18a33b69b2a5546c5c0dc8.png)
Hogy a ns nagyságrendű időtolás kényelmesebben kezelhető legyen, egy kb. 600-szoros időnyújtást alkalmazunk, aminek megvalósításához az eredeti- és a fáziseltolt jeleket egy 59,9 MHz-es jellel keverjük:
Legyen a fényforrásra érkező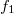 
= 60 MHz-es vezérlő feszültség 
, ahol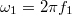 
. (Az egyszerűség kedvéért a továbbiakban az amplitúdókkal nem foglalkozunk.) Mivel a fény véges sebességgel terjed, a fotodióda 
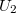jele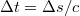 
idővel késik 
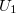-hez képest, ami 
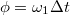fáziskésésnek felel meg, azaz 
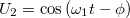. Ha most 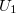-et és 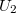-t az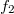 
= 59,9 MHz-es jellel szorozzuk ("keverjük"), akkor az
![\[U_1 ' = \cos [( \omega_1 + \omega_2 ) t] + \cos [( \omega_1 - \omega_2 ) t ] \]](/images/math/e/0/f/e0fa6c59c70a8ddfc9062b0f7e3ca8da.png)
![\[U_2 ' = \cos [( \omega_1 + \omega_2 ) t - \phi] + \cos [( \omega_1 - \omega_2 ) t - \phi ] \]](/images/math/5/0/e/50e60c82a61d45ab05b39439e41126c1.png)
összetett jeleket kapjuk, ahol kihasználtuk a szögfüggvényekre vonatkozó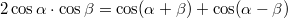 
összefüggést. Az összegfrekvencia igen magas (
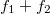= 119,9 MHz), amit szűrőkkel elnyomunk. A különbségi frekvenciához tartozó (
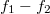= 100 kHz) komponenseket, az
![\[U_1 ' = \cos [( \omega_1 - \omega_2 ) t ]\]](/images/math/f/1/b/f1b8b88903d4e203378200b01dfe2727.png)
referenciajelet és a
![\[U_2 ' = \cos [( \omega_1 - \omega_2 ) t - \phi ]\]](/images/math/3/3/8/3387ceb90027e7d9d88dffc29c03d2c3.png)
késleltetett jelet pedig oszcilloszkópon jelenítjük meg. Vegyük észre, hogy a fázistolás állandó maradt. Így a hozzá tartozó időtolás 600-szorosára nőtt, miközben a frekvenciák 600-ad részükre csökkentek, azaz bármely jobb oszcilloszkópon megjeleníthetők.
A fentiek értelmében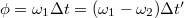 
, azaz
![\[\Delta t' = \frac{\omega_1}{\omega_1 - \omega_2} \Delta t = 600 \Delta t \]](/images/math/8/2/e/82eb155172ed2d2ca77beadc935fc5ac.png)
vagyis az oszcilloszkópon látott = 1 μs idő = 1/600 μs ≈ 1,6×10-9 s tényleges időkésésnek felel meg.
Összefoglalva: Az a idő, ami alatt a fény megteszi a két fotodióda közti távolságot, nem egyéb, mint a kevert alacsonyfrekvenciás jelek oszcilloszkópon észlelt fáziskülönbségének megfelelő időtolás (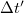
) és az időnyújtási faktor (600) hányadosa.
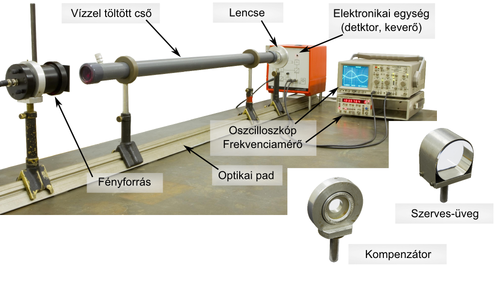
A mérőberendezés bemutatása és használata
Az összeállított mérőeszköz és annak vázlatos rajza a 2. és 3. ábrákon látható.
Részei:
- fényforrás + tartó ("lovas")
- fényérzékelő/elektronika egység
- Tektronix TBS1052B-EDU oszcilloszkóp
- koaxiális kábelek BNC csatlakozókkal (1 db 6 m-es, 2 db 1,5 m-es)
- optikai pad mm-skálával
- 150 mm fókusztávolságú lencse + tartó ("lovas")
A mérésnél használt további eszközök:
- szerves üveg tömb + tartó ("lovas")
- kétablakú vízzel töltött cső + tartók
- HAMEG frekvenciamérő
Az eszköz összeállítása
Állítsa lábaira a fényérzékelő/elektronikai egységet, majd helyezze az optikai pad végéhez úgy, hogy az lehetőség szerint merőleges legyen az előlapra! Rögzítse a fényforrást az optikai padon kb. 1 m-re a fényérzékelőtől! Kapcsolja össze a fényforrást, az elektronikai dobozt és az oszcilloszkópot a mellékelt koaxiális kábelekkel a 3. ábra szerint, úgy, hogy a 6 m-es (1. kábel) legyen a fényforrás és az elektronikai doboz a csatlakozói között, míg az 1,5 m-esek (2. kábelek) az elektronika és az oszcilloszkóp közt! Földelje az oszcilloszkóp mindkét csatornáját (GND), majd állítsa a nullvonalakat a képernyő közepére úgy, hogy fedjék egymást! Ekkor kapcsolja mindkét csatornát váltófeszültségre (AC), 0,5 V/cm-re, és az időlépést 2 μs/cm-re! Csatlakoztassa és kapcsolja az elektronikát a hálózati feszültségre. (Az előlap jelzőlámpája és a fényforrás LED-je világít.) Ekkor egy kb. 100 kHz-es jel (referencia jel) látható az oszcilloszkóp képernyőjén.
Az optikai út beállítása
A fényforrást és az előtte levő kondenzor lencsét úgy állítsa be, hogy a vörös fényfolt az elektronikai doboz előlapjára essen! Helyezze a 150 mm-es lencsét a fénysugár útjába! A fényforrás, a lencse és a fényérzékelő bemente legyenek azonos magasságban. A beállítás megkönnyítésére helyezzen papírlapot a fényérzékelő bemeneti nyílása (3. ábra, d) elé! Úgy állítsa a kondenzort és a fényforrást, hogy a 150 mm-es lencse a fénysugarat a bemeneti nyílásra fókuszálja! Ezután mozgassa 13 mm-rel az előlap felé a lencsét (ui. a fotodióda 13 mm mélyen van a bemeneti nyílás mögött)! Ha elveszi a papírlapot egy újabb 100 kHz-es jel jelenik meg az oszcilloszkóp II csatornáján (ld. 4. ábra), melynek amplitúdója még meglehetősen kicsi lehet. Ezt a jelet vizsgáljuk a továbbiakban.
Mozgassuk addig a lencsét, míg a II csatornán látható jel amplitúdója maximális lesz! A fényforrás hátlapján levő csavarok állításával is keresse meg az érzékelőre eső fényintenzitás maximumát! (Helyes beállítás esetén a csúcstól-csúcsig feszültség ~ 4 V.)
Megjegyzések:
- Az oszcilloszkóp időskálája kalibrált állásban legyen.
- A mérés előtt a két jel nullpontjai a fázistoló gomb segítségével fedésbe hozhatók. Ezzel kompenzáljuk a koaxiális kábelek és az optikai rendszer eredő fázistolását.
- A jelnek a referenciajelhez viszonyított eltolódása a nullátmenetek távolsága alapján határozható meg.
A mérés végrehajtása
a) Az időnyújtási tényező mérése: Bár a 60 MHz-es alapfrekvenciát és az 59,9 MHz-es keverő frekvenciát a berendezés nagy pontossággal állítja elő, a különbségi frekvencia hibája értelemszerűen nagyobb. Minthogy az időnyújtási tényező értéke és pontossága ettől függ, célszerű a különbségi frekvenciát közvetlenül mérni. Ez az elektronikai doboz b kimenetére csatlakoztatott frekvenciamérő segítségével történik.
b) A levegőre vonatkozó fénysebesség mérése:
Állítsa az időosztást 1 μs/cm-re. A fázistolóval hozza fedésbe a jel nullpontjait a referencia jel nullpontjaival. A fényforrás mozgatásával vegye fel a időtolást az optikai út 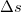hosszának függvényében.
c) Törésmutató mérése: A fázistolóval hozza fedésbe a mérendő jel nullpontjait a referencia jel nullpontjaival. (A folyadék törésmutatójának meghatározásánál a nullázást a folyadéktartó edény kétszeres falvastagságának megfelelő üveglap fényútba helyezésével végezze.) Helyezze a fényforrás és érzékelő közé a vizsgálandó mintát (szerves-üveg tömb vagy folyadékkal teli edény), és határozza meg az időtolást.
Mérési feladatok
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
FELADATOK ELSŐ ALKALOMMAL
1. A függvénygenerátor segítségével állítson be az oszcilloszkópon
a) 2 V amplitúdójú, 4 kHz-es szinuszjelet,
b) 500 mV amplitúdójú, 15 kHz-es háromszögjelet,
c) 3 V amplitúdójú, 500 Hz-es négyszögjelet!
- Minden mennyiséget az oszcilloszkóppal mérjen! A jelgenerátor adatai csak tájékoztató értékek.
- Frekvenciát nem tud közvetlenül mérni. Számítsa ki a beállítandó frekvenciákhoz tartozó periódusidőket, és azokat állítsa be!
- Rajzola le a képernyőn látott jelalakokat, és jegyezze fel a függőleges erősítő és az időalap kapcsoló állását! Határozza meg a beállítások hibáját! (Az oszcilloszkópot tekintse pontosnak, a hiba a leolvasásból adódik.)
2. A függvénygenerátoron állítson be 1 kHz-es szinuszjelet és csatlakoztassa az 1. függőleges bemenetre! Ugyanezt a jelet a fázistolón keresztül csatlakoztassa a 2. függőleges bemenetre (most X bemenet). (5) X-Y benyomásával és a fázistolón a fázis változtatásával a 6. ábrán látható jelalakokat állíthat elő. Állítson be egy-egy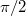 
-nél kisebb és nagyobb, általános helyzetet, és számítsa ki a hozzájuk tartozó fáziskülönbségeket!
- A fázistoló 20 V egyenfeszültséggel működik, amit az egyenfeszültségű tápegységen kell beállítani. A fekete dugót kell a "–" kivezetésbe dugni.
- Rajzolja le a megfigyelt jelalakot! Jegyezze fel most is a kapcsolók állását, és a közvetlenül mért adatok hibáját!
3. A "Gyengeáram" feliratú fali csatlakozóból vett szinuszjel frekvenciáját állapítsa meg Lissajous-módszerrel! A függvénygenerátor jelének változtatásával állítsa be a 7. ábrán látható jelek egyikét, rajzolja le és számolja ki az ismeretlen jel frekvenciáját!
- A "Gyengeáram" feliratú aljzatban a "–" kivezetés a föld.
- A referenciajel frekvenciáját az oszcilloszkóp segítségével határozza meg!
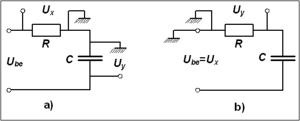
4. Állítsa össze a 10/a ábrán látható elrendezést! Mérje meg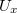 
és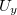 
feszültségek közötti fázisszöget! Az 
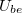jelet függvénygenerátorból vegye, legyen 5 V, 1 kHz, szinuszos!
- Az oszcilloszkóp bemenetei nem földfüggetlenek, ezért ha mindkét bementet használja, akkor a két földpontnak (fekete kivezetés) az áramkör ugyanazon pontjához kell csatlakoznia, különben a szkópon keresztül rövidre zárná az áramkör két pontját. (10/a és 10/b ábra)
- Rajzolja le a kapott ábrát és magyarázza meg, amit lát!
5. Ismételje meg az előző mérést a 10/b ábrának megfelelő összeállításban!
- Rajzolja le a kapott ábrát és magyarázza meg, amit lát!
6. Hangsebesség mérését 400 és 1200 Hz között 5 frekvencián végezze! Ábrázolja a hullámhosszt a frekvencia reciprokának függvényében! Illesszen a mérési pontokra egyenest, és az egyenes meredekségéből állapítsa meg a hang sebességét!
- A hangsebesség mérésénél a mikrofonerősítőhöz a 12 V-os tápfeszültséget az egyenfeszültségű tápegységből lehet venni. Mielőtt a tápfeszültséget rákapcsolja az erősítőre ne felejtse el a tápegységet átállítani 20 V-ról 12 V-ra!
FIGYELEM! A második alkalomra az eddigi feladatok előzetes kiértékelését el kell végezni és meg kell mutatni a mérésvezetőnek.
FELADATOK MÁSODIK ALKALOMMAL
1. Állítsa össze a mérőeszközt, állítsa be az oszcilloszkópot és az optikai elemeket!
- Az oszcilloszkópot melyik jelre érdemes triggerelni? Ha egy zajjal terhelt szinusz jelre triggerelünk, akkor milyen trigger szint mellett lesz a legkisebb illetve a legnagyobb az időmérés hibája?
- A mérési naplóba mindig jegyezze fel az oszcilloszkóp beállításait!
2. Mérje meg a különbségi frekvenciát! Ennek ismeretében határozza meg az időnyújtási tényező pontos értékét!
- A 60 MHz-es alapfrekvencia pontosnak tekinthető.
3. Határozza meg a levegőre vonatkozó fénysebességet a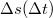 
függvénykapcsolat meredekségéből!
- Ezt a mérést csak az optikai elemek precíz beállítása mellett lehet pontosan elvégezni. A fényforrást nem elég egy adott pozíciónál a detektorra fókuszálni, hanem a fényforrás akár 1m-es mozgási tartományában végig a detektorra fókuszált jel mellett kell mérni. Ha ez nem teljesül, akkor elképzelhető hogy bizonyos pozícióknál a direkt nyalábnak csak kis része jut el a detektorba, ekkor elképzelhető, hogy a mért jel nagy részét többszörösen visszaverődő nyaláb, vagy a következő pontban ismertetett háttérjel adja.
- A mérési elektronikán belül előfordulhatnak áthallások, azaz akkor is mérünk 100kHz-es jelet, ha a detektort teljesen kitakarjuk. Határozzuk meg ennek a háttérjelnek az amplitúdóját. Ügyeljünk arra, hogy a mérés során a detektor végig ennél a zavaró háttérjelnél lényegesen nagyobb jelet mutasson (azaz a fényforrás jelének nagy része eljusson a detektorba).
- A mérést igyekezzünk a lehető legérzékenyebb oszcilloszkóp beállítások mellett elvégezni, azaz alkalmazzuk a lehető legkisebb időalapot és a lehető legnagyobb feszültségerősítést.
4. Határozza meg a szerves-üveg minta levegőre vonatkoztatott törésmutatóját!
- Vegye figyelembe, hogy törésmutató a közegekben vett fénysebességek hányadosa!
- Ez a mérés a mérőeszköz felbontóképességének határán mozog, így különösen ügyeljünk az optikai rendszer és az oszcilloszkóp optimális beállítására, illetve a mérési hiba reális meghatározására.
5. Határozza meg a víz levegőre vonatkoztatott törésmutatóját!
