Optikai mérések
A mérés célja:
- elmélyíteni a hallgatók geometriai optikai ismereteit,
- megismerkedni a folyadékkristályok tulajdonságaival és egyszerű elektrooptikai mérésekkel.
Ennek érdekében:
- áttekintjük a fénytörés és visszaverődés elméletét,
- geometriai optikai méréseket végzünk,
- vizsgáljuk a polarizált fény visszaverődését.
- röviden bemutatjuk a nematikus folyadékkristály tulajdonságait,
- optikai és elektrooptikai méréseket végzünk különböző folyadékkristály cellákkal.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Geometriai optika alapjai
Egy fényforrásból adott térszögben ( ) kiinduló fénynyaláb végtelen kicsi térszöghöz (
) kiinduló fénynyaláb végtelen kicsi térszöghöz (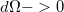 ) tartozó határesetét fénysugárnak, ezek terjedésével foglalkozó területet pedig geometriai optikának hívjuk. Matematikailag a fénysugár egy olyan görbe, amelynek egy adott pontbeli érintője megegyezik a fény adott pontbeli terjedési irányával. Gyakorlati szempontból a fényforrástól elég távol úgy tekinthetjük, hogy a fényforrás minden irányba fénysugarakat bocsát ki. A geometriai optika alaptörvényei:
) tartozó határesetét fénysugárnak, ezek terjedésével foglalkozó területet pedig geometriai optikának hívjuk. Matematikailag a fénysugár egy olyan görbe, amelynek egy adott pontbeli érintője megegyezik a fény adott pontbeli terjedési irányával. Gyakorlati szempontból a fényforrástól elég távol úgy tekinthetjük, hogy a fényforrás minden irányba fénysugarakat bocsát ki. A geometriai optika alaptörvényei:
- Homogén közegben a fény egyenes vonalban terjed.
- A tér egy pontján akárhány fénysugár áthaladhat egymás zavarása nélkül.
- Ha a fénysugár a tér egyik pontjából egy bizonyos útvonalon halad a tér másik pontjába, akkor az onnan visszafelé indított fénysugár ugyanazon az úton fog haladni.
- A fény véges sebességgel terjed, aminek értéke függ a közegtől. A fénysebessége vákuumbeli értéke
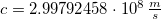 (közelítőleg
(közelítőleg 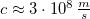 ). Az ún. abszolút (vákuumra vonatkoztatott) törésmutató (
). Az ún. abszolút (vákuumra vonatkoztatott) törésmutató ( ) pedig a vákuumbeli
) pedig a vákuumbeli  fénysebesség és az adott közegbeli
fénysebesség és az adott közegbeli 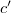 fénysebesség hányadosa:
fénysebesség hányadosa:![\[n=\frac{c}{c'}.\]](/images/math/1/d/4/1d4f545120d9a1ee24778f29146fda9d.png)
Leképzés optikai lencsékkel
Görbült felületek esetében a fénytörés szintén a törési törvény alapján számítható, de ekkor a beesési merőleges helyről helyre változik.
A törési törvény alapján levezethető, hogy egy 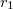 és
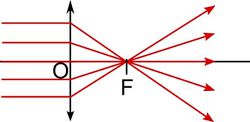
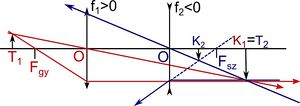
és 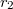 görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha
görbületi sugarú gömbfelülettel határolt vékony lencse az optikai tengelyhez közeli párhuzamos fénysugarakat egy pontba (a fókusz- vagy gyújtópontba) gyűjti, ha 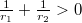 . (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a 8 ábrán láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az
. (Domború felület görbületi sugarát pozitívnak, homorú felületét negatívnak tekintjük.) A sugármenetek a 8 ábrán láthatók, a gyűjtőlencsét kettős nyíl jelöli. Az 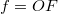 fókusztávolság, a lencse anyagának
fókusztávolság, a lencse anyagának  törésmutatója és a görbületi sugarak között az
törésmutatója és a görbületi sugarak között az
![\[ \frac{1}{f} = (n-1)\left(\frac{1}{r_1}+\frac{1}{r_2} \right) \]](/images/math/8/4/a/84a0e9228d0b072744ebe46bedec6cf1.png)
összefüggés áll fent.
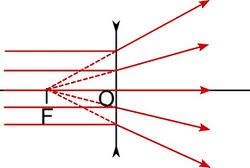
Ha 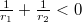 , akkor
, akkor 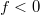 , és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának (9. ábra).
, és a lencse a párhuzamosan érkező fénysugarakat úgy szórja, mintha egy pontból (a fókuszpontból) indulnának (9. ábra).
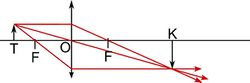
A gyűjtőlencse egy, a fókuszpontnál távolabbi pontból kiinduló fénysugarakat egy másik pontban gyűjti össze és így létrejön a  tárgy valódi (ernyőn megjeleníthető)
tárgy valódi (ernyőn megjeleníthető)  képe (amely a nevezetes sugarak megrajzolásával könnyen megszerkeszthető, 10. ábra). A
képe (amely a nevezetes sugarak megrajzolásával könnyen megszerkeszthető, 10. ábra). A 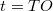 tárgytávolság, a
tárgytávolság, a 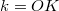 képtávolság és az
képtávolság és az  fókusztávolság között az
fókusztávolság között az
![\[ \frac{1}{t} + \frac{1}{k} = \frac{1}{f} \]](/images/math/0/e/7/0e73cce9cbf37f16a8c5467cd34538fc.png)
leképezési törvény teremt kapcsolatot.
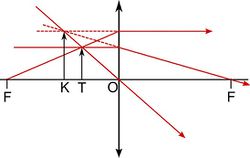
A képlet akkor is használható, ha 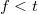 vagy ha
vagy ha  negatív. Ekkor
negatív. Ekkor  -ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik (11. ábra).
-ra negatív érték adódik, és ernyőn nem megjeleníthető, látszólagos kép keletkezik (11. ábra).
Több lencséből álló leképzésnél az első lencse képe a második lencse tárgya lesz. Ilyenkor, ha az első lencse által létrehozott valódi kép a második lencse mögött keletkezne, akkor 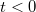 is előfordulhat ("látszólagos tárgy").
is előfordulhat ("látszólagos tárgy").
Gyűjtőlencse fókusztávolságának mérése
Ha a 10. ábrának megfelelő elrendezésben egy tárgyról valódi képet hozunk létre, megmérjük a  tárgytávolságot, és a
tárgytávolságot, és a  képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható.
képtávolságot, akkor a leképezési törvény alapján a gyűjtőlencse fókusztávolsága kiszámítható. Ha a tárgy egy jól megvilágított, kontrasztos, sík ábra, és az ernyő, amin a kép keletkezik, szintén sík felület, akkor ezek helye jól mérhető. A lencse helyét viszont nem lehet ilyen pontosan mérni, hiszen egy vékony lencsének is van vastagsága, és a lencse középsíkja a befogás miatt is nehezen megállapítható.
Ezt a nehézséget küszöböli ki a következő mérési eljárás: Állítsuk a tárgyat és az ernyőt egymástól  távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha
távolságra (ez a távolság – két sík között – könnyen mérhető). Mozgassuk a lencsét a tárgy és az ernyő között. Ha 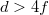 , akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.)
A megfelelő tárgy- és képtávolságokat jelölje
, akkor a lencse két helyzetében is éles képet kapunk. (Egy nagyított és egy kicsinyített kép keletkezik.)
A megfelelő tárgy- és képtávolságokat jelölje 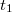 ,
, 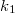 ill.
ill. 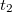 ,
, 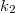 . A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig
. A lencse két éles képet adó helyzete közötti (szintén könnyen mérhető) elmozdulását pedig 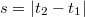 . Felhasználva, hogy a szimmetria miatt
. Felhasználva, hogy a szimmetria miatt 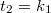 (és
(és 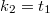 ):
):
![\[ \frac{1}{t_1} + \frac{1}{k_1} = \frac{1}{f}, \]](/images/math/4/b/9/4b9d59ca70cd713830a03cfacdb5d7a6.png)
![\[ t_1 + k_1 = d, \]](/images/math/a/7/e/a7e3335c77a51ab42b3045073e1ccd87.png)
![\[ |t_1 - k_1| = s. \]](/images/math/3/b/0/3b0499ef281b72fda0118dfe576b7c0c.png)
Az egyenletekből 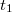 -et és
-et és 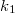 -et kiküszöbölve:
-et kiküszöbölve:
![\[ f = \frac{d^2-s^2}{4d}, \]](/images/math/0/d/f/0df5c748777c483d967c242cf30ec45d.png)
tehát a fókusztávolság  és
és  ismeretében kiszámítható.
ismeretében kiszámítható.
Szórólencse fókusztávolságának mérése
Szórólencsével nem lehet ernyőn megjeleníthető valódi képet létrehozni, így a képtávolságot nem tudjuk mérni. Egy gyűjtő- és egy szórólencséből azonban összeállítható olyan lencserendszer, amely valódi képet ad (12. ábra). A 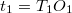 , a
, a 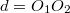 és a
és a 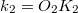 távolság mérhető.
távolság mérhető.
Felhasználva, hogy
![\[ t_2 = d - k_1 < 0 \]](/images/math/9/5/0/950b3f9ee4e4968e9e4aad051354337f.png)
és felírva a két lencse leképzési törvényét 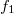 ,
, 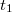 ,
,  és
és 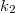 segítségével a szórólencse fókusztávolsága kifejezhető.
segítségével a szórólencse fókusztávolsága kifejezhető.
Törésmutató mérése a teljes visszaverődés határszögének meghatározásával
Két közeg sík határfelületén a fény a
![\[ \sin \alpha = n_{12}\sin \beta \]](/images/math/f/0/3/f03eb5697d3a9c19ee18f025825d8b38.png)
törési törvény (Snellius - Descartes törvény) szerint megtörik. Az összefüggésben  és
és  a belépő és a megtört fénysugarak beesési merőlegessel bezárt szögét,
a belépő és a megtört fénysugarak beesési merőlegessel bezárt szögét, 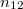 pedig a két közeg relatív törésmutatóját jelöli. A relatív törésmutató a két közeg abszolút törésmutatójának hányadosa:
pedig a két közeg relatív törésmutatóját jelöli. A relatív törésmutató a két közeg abszolút törésmutatójának hányadosa:
![\[ n_{12} = \frac{n_{2}}{n_{1}}. \]](/images/math/f/c/c/fcc73de627160897a6c60cb60a485d7d.png)
Ha a határfelületre az optikailag sűrűbb (s) közegből érkezik a fény, akkor a relatív törésmutató 1-nél kisebb. Ekkor a törési törvény alapján a fény csak akkor léphet be az optikailag ritkább (r) közegbe, ha
![\[ \alpha < \alpha_h \]](/images/math/e/a/a/eaaa8e53353bf8b8c17303905d610b89.png)
ahol 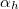 a teljes visszaverődés határszöge. A törési törvény alapján
a teljes visszaverődés határszöge. A törési törvény alapján
![\[ \sin \alpha_h = n_{sr} = \frac{1}{n_{rs}}. \]](/images/math/4/d/f/4df51c882b13ab7180cc1c838505c983.png)
Ha a beesési szög a határszögnél nagyobb, akkor a beeső fény teljesen visszaverődik. Az előző összefüggés alapján a határszög mérésével a relatív törésmutató meghatározható.
A mérési módszer
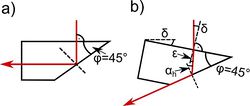
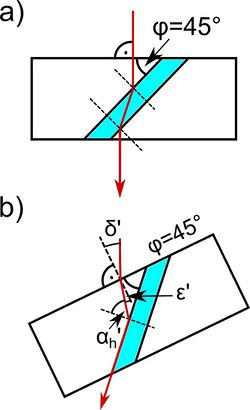
Az 7. ábrán látható, forgatható asztalra tett 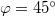 törőszögű prizmára először merőlegesen esik a lézerfény. (A merőleges beesést úgy lehet beállítani, hogy ilyenkor a részlegesen visszaverődő nyaláb éppen a lézerbe verődik vissza.) A merőlegesen belépő fénysugár törés nélkül lép be az üvegbe, majd a másik határfelületen teljesen visszaverődik, végül a prizma bal oldalán, szintén törés nélkül, kilép (5. ábra).
törőszögű prizmára először merőlegesen esik a lézerfény. (A merőleges beesést úgy lehet beállítani, hogy ilyenkor a részlegesen visszaverődő nyaláb éppen a lézerbe verődik vissza.) A merőlegesen belépő fénysugár törés nélkül lép be az üvegbe, majd a másik határfelületen teljesen visszaverődik, végül a prizma bal oldalán, szintén törés nélkül, kilép (5. ábra).
Az asztal (és a prizma) megfelelő szöggel való elforgatásával elérhető, hogy a fénysugár már nem verődik vissza teljesen, hanem 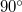 -os törési szöggel, a felületet súrolva, kilép az üvegből.
-os törési szöggel, a felületet súrolva, kilép az üvegből.
Ekkor a következő összefüggéseket írhatjuk fel:
![\[ \sin \delta = n_u \sin \varepsilon, \]](/images/math/f/d/c/fdc23f8338b8a35adf2aecdf2cacc860.png)
![\[ \alpha_h + \varepsilon = \varphi = 45^\circ, \]](/images/math/f/e/3/fe33ee236587008cee7e8dba48196d9a.png)
![\[ \sin \alpha_h = \frac{1}{n_u}. \]](/images/math/2/4/a/24a54c91407c10daf5cf29ea9d89c3fb.png)
A három összefüggés alapján 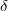 mérésével az üveg levegőre vonatkoztatott
mérésével az üveg levegőre vonatkoztatott 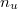 törésmutatója (valamint az
törésmutatója (valamint az  szög és az
szög és az 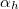 határszög) meghatározható.
határszög) meghatározható.
A 6 ábrán látható elrendezés két ugyanilyen prizmából van összeállítva. A két prizma közé folyadék önthető. A fénysugár most is először merőlegesen, törés nélkül lép be az üvegbe, majd megtörve belép a folyadékba, ismét megtörve átlép a másik prizmába, végül (törés nélkül) kilép a levegőbe.
Az asztal (és a prizma) megfelelő szöggel való elforgatásával ekkor is elérhető, hogy a fénysugár éppen 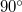 -os törési szöggel, a felületet súrolva lép ki az üvegből. A fenti összefüggések ekkor így módosulnak:
-os törési szöggel, a felületet súrolva lép ki az üvegből. A fenti összefüggések ekkor így módosulnak:
![\[ \sin \delta^\prime = n_u \sin \varepsilon^\prime, \]](/images/math/4/6/9/4697ba19810e5b150bd381d246bd966a.png)
![\[ \alpha_h^\prime - \varepsilon^\prime = \varphi = 45^\circ, \]](/images/math/4/a/6/4a69bd4bfb26d66f1fd02e74c6049ea8.png)
![\[ \sin \alpha_h^\prime = \frac{n_f}{n_u}. \]](/images/math/7/1/4/714c6c29288cfa49a93e48f812a51558.png)
Az előző mérésből 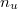 ismert, így a három összefüggés segítségével
ismert, így a három összefüggés segítségével 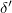 mérésével a folyadék levegőre vonatkoztatott törésmutatója (valamint az
mérésével a folyadék levegőre vonatkoztatott törésmutatója (valamint az  szög és az
szög és az 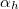 határszög) meghatározható.
határszög) meghatározható.
Folyadékkristályok bemutatása
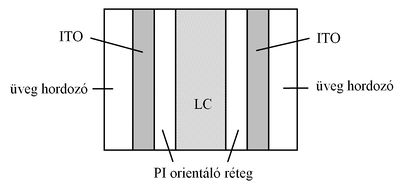
A folyadékkristály (LC = Liquid Crystal) olyan állapota az anyagnak, ami a kristályos szilárd állapot és az amorf folyadék állapot között van. A nematikus LC-k szerves vegyületek, melyek hosszúkás, tűszerű molekulákból állnak. A molekulák orientációja (irányítottsága) könnyen egy irányba rendezhető és szabályozható elektromos erőtér segítségével. Az LC eszközökhöz azonos vagy jól meghatározott orientációjú LC molekulákra van szükség. A méréshez használt LC cella felépítése az 1. ábrán látható. Az üveg hordozólemezeket először egy vékony, elektromosan vezető, de optikailag átlátszó indium-ón-oxid (ITO = Indium-Tin-Oxide) réteggel vonják be, majd egy vékony polyimid (PI) rendező réteget alakítanak ki. Ezután a PI réteg felszínét megcsiszolják, és ezzel mikroszkopikus árkokat alakítanak ki rajta. Ezek az árkok rendezik egy irányba az LC molekulákat, melyeket szendvicsszerűen két hordozó közé helyeznek. Ezzel a csiszolásos módszerrel a kívánt irányba orientált, jól rendezett LC-molekulák kerülnek a hordozók felszínére, és a molekulák közt ható erők hatására az egész LC-hasáb azonos orientációjú lesz. Egy adott helyen a molekula-orientációt az LC adott helyen lévő direktorának nevezik.
Az LC cellában megfigyelhető az ún. kettőstörés jelensége, amikor az anyagnak kétféle fő törésmutatója van. Ha a fény a direktor irányában terjed, akkor az összes polarizációs összetevő ugyanakkora 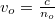 sebességgel terjed, ahol
sebességgel terjed, ahol 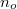 az ordinárius (rendes) törésmutató. Ezt a terjedési irányt (a direktor irányát) nevezik a cella optikai tengelyének. Ha a fény az optikai tengelyre merőleges irányba terjed, akkor két terjedési sebesség van. A fény elektromos mezejének az optikai tengelyre merőlegesen polarizált része ekkor is
az ordinárius (rendes) törésmutató. Ezt a terjedési irányt (a direktor irányát) nevezik a cella optikai tengelyének. Ha a fény az optikai tengelyre merőleges irányba terjed, akkor két terjedési sebesség van. A fény elektromos mezejének az optikai tengelyre merőlegesen polarizált része ekkor is 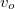 sebességgel halad, az optikai tengellyel párhuzamosan polarizált rész sebessége viszont
sebességgel halad, az optikai tengellyel párhuzamosan polarizált rész sebessége viszont 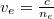 , ahol
, ahol 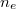 az extraordinárius (különleges) törésmutató. Az optikai anizotrópia (pontosabban annak mértéke) az extraordinárius és az ordinárius törésmutató különbsége:
az extraordinárius (különleges) törésmutató. Az optikai anizotrópia (pontosabban annak mértéke) az extraordinárius és az ordinárius törésmutató különbsége: 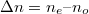 .
.
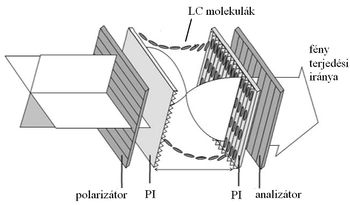
Az LC cella optikai viselkedése a cella elé helyezett polarizátor és a cella mögé helyezett analizátor polárszűrők segítségével vizsgálható.
90°-kal elcsavart nematikus LC cella
A 90°-kal elcsavart nematikus cellában (3. ábra) (TN = Twisted Nematic) a hátsó felület LC direktora 90°-kal el van forgatva az első felülethez képest. Elől a helyi direktor párhuzamos a polarizátor (első polárszűrő) polarizációs irányával. A belépő polarizálatlan fény az első polárszűrőben lineárisan polarizált fénnyé változik.
Ha egy lineárisan polarizált fény halad át egy 90° TN cellán, akkor polarizációs iránya követi az LC direktorának csavarodását (a polarizált fény csak 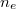 -t érzékeli), így a kilépő fénysugár is lineárisan polarizált marad, csak polarizációs iránya 90°-kal elfordul. (Ezt
-t érzékeli), így a kilépő fénysugár is lineárisan polarizált marad, csak polarizációs iránya 90°-kal elfordul. (Ezt 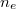 által okozott polarizációs forgató hatásnak nevezzük, ehhez hasonlóan van
által okozott polarizációs forgató hatásnak nevezzük, ehhez hasonlóan van 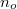 által okozott forgató hatás is.) Eszerint a 90° TN cella normál fekete (NB = Normal Black) üzemmódjához az analizátor (a második polárszűrő) polarizációs irányát párhuzamosra kell állítani a polarizátor (az első polárszűrő) polarizációs irányával.
által okozott forgató hatás is.) Eszerint a 90° TN cella normál fekete (NB = Normal Black) üzemmódjához az analizátor (a második polárszűrő) polarizációs irányát párhuzamosra kell állítani a polarizátor (az első polárszűrő) polarizációs irányával.
Azonban ha az LC cellára kapcsolt  feszültség értéke elér egy kritikus
feszültség értéke elér egy kritikus 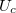 értéket, az LC molekulák igyekeznek beállni az alkalmazott külső elektromos tér irányába, ami itt megegyezik a fény terjedési irányával. Ennél fogva az LC cella polarizációs irányt elforgató hatása folyamatosan csökken, és a fény átjuthat az analizátoron (a második polárszűrőn). A cella elektro-optikai kapcsolási meredekségét a
értéket, az LC molekulák igyekeznek beállni az alkalmazott külső elektromos tér irányába, ami itt megegyezik a fény terjedési irányával. Ennél fogva az LC cella polarizációs irányt elforgató hatása folyamatosan csökken, és a fény átjuthat az analizátoron (a második polárszűrőn). A cella elektro-optikai kapcsolási meredekségét a 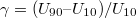 képlet definiálja, ahol
képlet definiálja, ahol 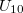 és
és 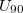 azok a feszültségek, ahol a cellán áthaladó fény intenzitása eléri a maximális fényintenzitás 10 %-át illetve 90 %-át.
azok a feszültségek, ahol a cellán áthaladó fény intenzitása eléri a maximális fényintenzitás 10 %-át illetve 90 %-át.
Megjegyzendő, hogy egyenfeszültség alkalmazása esetén elektrolízis indulna be a cellában, mely a cella károsodásához vezetne. Emiatt a cella kapcsolásához váltófeszültséget használunk.
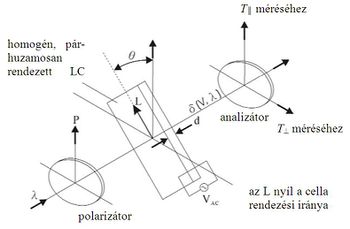
Homogén, párhuzamosan rendezett LC cella
A párhuzamosan rendezett LC cella esetében az elülső és a hátsó hordozón lévő direktorok párhuzamosak egymással. Ha egy polarizált fénysugár úgy esik a párhuzamosan rendezett cellára, hogy polarizációs iránya párhuzamos az LC cella direktorával (a csiszolt vájatok irányával), akkor semmi lényeges változás nem történik, mivel a fény tisztán extraordinárius sugárként viselkedik.
Másrészt, ha egy lineárisan polarizált fénysugár merőlegesen esik a párhuzamosan rendezett cellára, de polarizációs iránya 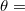 45° szöget zár be a cella direktorának irányával (4. ábra), akkor fáziskülönbség (
45° szöget zár be a cella direktorának irányával (4. ábra), akkor fáziskülönbség (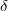 ) lép fel az extraordinárius és az ordinárius sugarak különböző terjedési sebessége miatt. Ebben a
) lép fel az extraordinárius és az ordinárius sugarak különböző terjedési sebessége miatt. Ebben a 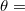 45°-os elrendezésben, ha a két polárszűrő egymással párhuzamos ill. merőleges, akkor a rendszer fényáteresztő képességét a következő összefüggések írják le:
45°-os elrendezésben, ha a két polárszűrő egymással párhuzamos ill. merőleges, akkor a rendszer fényáteresztő képességét a következő összefüggések írják le:
![\[ T_\parallel = 1-\sin^2 2\theta \sin^2 \frac{\delta}{2} = \cos^2 \frac{\delta}{2}, \]](/images/math/8/f/4/8f4abf5c6bdb798c0af27ad5c0b5279a.png)
![\[ T_\perp= \sin^2 2\theta \sin^2 \frac{\delta}{2} = \sin^2 \frac{\delta}{2}, \]](/images/math/9/a/2/9a2c6148219fbc2ff73e49104b8a715a.png)
ahol 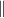 és
és 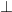 az analizátor és a polarizátor polarizációs irányának párhuzamos ill. merőleges állására utal.
az analizátor és a polarizátor polarizációs irányának párhuzamos ill. merőleges állására utal.
A 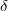 fáziskülönbség kifejezhető:
fáziskülönbség kifejezhető:
![\[ \delta = \frac{2\pi d \Delta n(U,\lambda)}{\lambda}, \]](/images/math/9/4/f/94fddaf297fb0ffc47dfa953e3bace75.png)
ahol  az LC réteg vastagsága,
az LC réteg vastagsága,  a fény hullámhossza levegőben,
a fény hullámhossza levegőben,  a váltakozó feszültség effektív értéke, és
a váltakozó feszültség effektív értéke, és 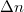 (ami
(ami  és
és  függvénye) az LC cella optikai anizotrópiájának mértéke. Azt is meg kell jegyezni, hogy ha
függvénye) az LC cella optikai anizotrópiájának mértéke. Azt is meg kell jegyezni, hogy ha 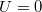 , akkor
, akkor 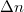 maximális, és így
maximális, és így 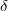 -nak is ekkor van maximuma. Tehát
-nak is ekkor van maximuma. Tehát 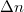 csökken, ha
csökken, ha  növekszik.
növekszik.
A méréshez használt egyéb optikai eszközök
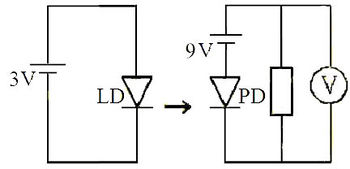
Lézerdióda
A méréshez használt fényforrás egy 650 nm hullámhosszúságú félvezető lézer. Ha a lézerdióda (LD) árama nagyobb egy küszöbáramnál (threshold current), a dióda monokromatikus, részlegesen polarizált, koherens fényt bocsát ki. Ha a lézerdióda árama kisebb a küszöbértéknél, a kibocsátott fény intenzitása nagyon kicsi. A küszöbáram felett a fényerősség az áramerősség növekedésével rohamosan nő, és a két mennyiség között lineáris kapcsolat van, egészen egy 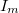 áramértékig. Ha az áram tovább nő, a fényerősség növekedési üteme a lézerdióda melegedése miatt (kis mértékben) csökken. A lézerdióda optimális működési tartománya az, ahol a fényerősség lineárisan függ az áramerősségtől. Az
áramértékig. Ha az áram tovább nő, a fényerősség növekedési üteme a lézerdióda melegedése miatt (kis mértékben) csökken. A lézerdióda optimális működési tartománya az, ahol a fényerősség lineárisan függ az áramerősségtől. Az 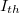 küszöbáram definíció szerint az áramerősség tengely és a lineáris tartományra illesztett egyenes meghosszabbításának metszéspontja.
A lézerfény csak részlegesen polarizált. A polarizáció mértékét a
küszöbáram definíció szerint az áramerősség tengely és a lineáris tartományra illesztett egyenes meghosszabbításának metszéspontja.
A lézerfény csak részlegesen polarizált. A polarizáció mértékét a 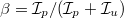 aránnyal lehet jellemezni, ahol
aránnyal lehet jellemezni, ahol 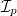 és
és 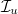 a lézerfény polarizált és polarizálatlan összetevőjének intenzitása.
a lézerfény polarizált és polarizálatlan összetevőjének intenzitása.
Fotodetektor
A méréshez használt fotodetektor egy fotodiódából és egy áramerősítőből áll. Ha a fotodiódára tápfeszültség van kapcsolva, akkor a diódára eső fény hatására áram generálódik (fotoáram). Állandó hőmérsékleten, monokromatikus fény estében a fotoáram egyenesen arányos a fényintenzitással. Az áramerősítő ezt a fotoáramot egy kimenő feszültségjellé alakítja. A fotodetektor kétféle erősítéssel működhet: "high" és "low". Azonban a fotodióda tulajdonságai miatt, ha a fényerősség nagyon nagy, a kimenő feszültség 8 V tájékán telítődik (nem nő tovább), ilyenkor a fotodióda már nem működik helyesen. Emiatt a fotodetektor akkor működik megfelelően, amikor a lineáris tartományban van. Ha a fényerősség olyan nagy, hogy a fotodióda eléri a telítődést, akkor a fotodetektor már nem mutatja helyesen a fényintenzitást.
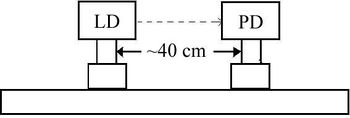
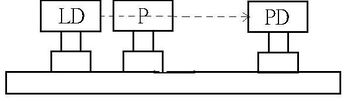
A lézerdióda (LD) és a fotodetektor (PD) elrendezése és elektromos kapcsolása az 5. és a 6. ábrán látható.
Polárszűrők
A forgatható foglalatba szerelt polárszűrők az áthaladó fényt lineárisan polarizálják. Az első polárszűrőt polarizátornak, a másodikat analizátornak szokás nevezni, de felépítésük azonos. A polárszűrő (P) optikai elrendezése a 7. ábrán látható.
Mérési feladatok
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
FIGYELEM! Ne nézzen bele közvetlenül a lézersugárba! Tönkreteheti a szemét!
FELADATOK ELSŐ ALKALOMMAL
Leképzés optikai lencsékkel
1. Helyezze a fényforrást és az ernyőt az optikai sín két végére! A tárgyat (diát) a fényforrás elé kb. 5 cm távolságba helyezze! Mérje meg a tárgy és az ernyő  távolságát! Helyezze el az (1) jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti
távolságát! Helyezze el az (1) jelű gyűjtőlencsét a tárgy és az ernyő közé, és a lencse mozgatásával keresse meg azt a két helyzetet, amikor éles kép keletkezik! Mérje meg a lencse két helyzete közti  távolságot, és határozza meg a lencse fókusztávolságát!
távolságot, és határozza meg a lencse fókusztávolságát!
- Figyelem! A mérésnél használt lovasok talpa nem azonos szélességű, így a távolságokat ne a lovas talpának szélénél olvassa le!
2. Helyezze az (1) jelű gyűjtőlencse és az ernyő közé a (2) jelű szórólencsét! Elméleti megfontolások után az ernyő és/vagy a lencsék megfelelő mozgatásával állítson elő éles képet! Mérje meg a tárgy, a lencsék és az ernyő közti távolságokat, és határozza meg a szórólencse fókusztávolságát!
- Figyelem! Ennél a mérésnél könnyen előfordulhat olyan beállítás, melynél a távolság mérésének kicsi hibája is óriási hibát okozhat a gyújtótávolság meghatározásakor. Ezt próbálja elkerülni elméleti megfontolások segítségével, vagy a mérés megismétlésével több lényegesen eltérő lencsepozíciónál. Ugyanezen okból a gyűjtőlencse által alkotott kép pozícióját célszerű az ernyő mozgatásával közvetlenül megmérni az előző mérésben meghatározott (hibával terhelt) fókusztávolság alapján történő közvetett számolás helyett.
3. A kis fókusztávolságú (3 jelű) lencse segítségével állítson össze minél nagyobb nagyítású leképzést! A tárgytartóba most az 5mm átmérőjű lyukat helyezze, melyen egy hajszál fut keresztül. A lyuk képének méretéből határozza meg a nagyítást, majd a hajszál képének szélességéből határozza meg a hajszál átmérőjét!
- Becsülje meg a mérés hibáját!
A méréshez rendelkezésre álló eszközök
- A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.
- Figyelem! Soha ne nézzen a lézernyalábba, mert az látáskárosodást okozhat!
Törésmutató mérése a teljes visszaverődés határszögének meghatározásával
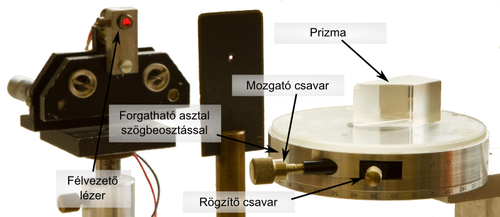
4. Tegye fel a forgatható asztalra a prizmát! Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a prizma anyagának levegőre vonatkoztatott törésmutatóját!
- A forgóasztal szögállása egy tolómérőhöz hasonló módon tizedfokos pontossággal olvasható le. A forgóasztalon egy rögzítő és egy mozgató csavar található. Finomhangoláshoz érdemes a mozgatócsavar középállásánál becsavarni a rögzítőcsavart, majd a mozgatócsavar finom állításával megkeresni a kívánt szöget. Figyelem! A szögérték leolvasásakor könnyen belenézhet a nyalábba, így a leolvasás előtt a lézert MINDIG KAPCSOLJA KI! A forgóasztal csavarjait ne erőltesse! Rögzített állásban kézzel ne próbálja forgatni az asztalt, ekkor csak a mozgatócsavarral lehet!
5. Cserélje ki a prizmát a két prizmából összeállított rendszerre! Öntsön a prizmák közé desztillált vizet. Állítsa be a lézernyalábot a prizma felületére merőlegesre! Az asztal forgatásával keresse meg a teljes visszaverődés határhelyzetét! Számítsa ki a határszöget és a víz levegőre vonatkoztatott törésmutatóját!
- Az üveg tipikus törésmutatója, illetve a víz ismert törésmutatója alapján számolja ki, hogy milyen elforgatási szögeknél várja a teljes visszaverődést! (Ezt a számolást hasznos a mérési gyakorlat előtt, otthon elvégezni.) A mért értéket hasonlítsa össze a várakozással! A kétprizmás elrendezésnél legyen kifejezetten körültekintő, hiszen a teljes visszaverődéstől független geometriai okokból is megjelenhet illetve eltűnhet egy levegőbe kilépő nyaláb a forgatás közben!
FIGYELEM! A második alkalomra az eddigi feladatok előzetes kiértékelését el kell végezni és meg kell mutatni a mérésvezetőnek.
FELADATOK MÁSODIK ALKALOMMAL
Folyadékkristályok vizsgálata
A mérés végén ne felejtse el kikapcsolni a lézert, és kivenni az elemet a fotodetektorból!
A lézerdióda és a fotodetektor beállítása és vizsgálata
1. Szerelje fel a lézerdiódát és a fotodetektort egy vízszintes egyenes mentés az optikai sínre, ahogy a 5. ábrán látható!
- Tegye be a fotodetektorba az elemet, csatlakoztassa a kézi multimétert (DC voltmérő állásban), és kapcsolja be a lézerdiódát!
- Állítsa be a lézerdióda és a fotodetektor magasságát úgy, hogy a lézersugár vízszintes legyen.
A lézerdiódán lévő csavarok segítségével állítsa be, hogy a lézerfény a detektoron lévő kis lyukba jusson, és a fotodetektor maximális értéket mutasson!
2. Szereljen fel egy polárszűrőt a lézerdióda és a fotodetektor közé, ahogy az a 7. ábrán látható! Győződjön meg róla, hogy a lézersugár a polárszűrő középső részén halad-e át! Állítsa be a polárszűrőt úgy, hogy a beeső fénysugár merőleges legyen a polárszűrő síkjára!
- Javaslat: Rakjon be egy lyukas papírt a fényútba, és ezen ellenőrizze, hogy a beeső és a visszavert sugár egybeesik-e!
Forgassa körbe a polárszűrőt, és mérje meg az 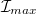 maximális és az
maximális és az 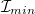 minimális fényintenzitást!
Határozza meg a lézerfényben a lineárisan polarizált fény
minimális fényintenzitást!
Határozza meg a lézerfényben a lineárisan polarizált fény  arányát!
arányát! 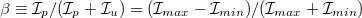 .
.
3. Állítsa be a polárszűrőt úgy, hogy a fényintenzitás maximális legyen! Szerelje fel a másik polárszűrőt is az optikai sínre és állítsa be ezt is a fénysugárra merőlegesen! Állítsa a második polárszűrő polarizációs irányát az elsővel párhuzamosra (forgassa addig, amíg a fényintenzitás maximális nem lesz)!
A 90° TN LC cella vizsgálata
4. Szerelje fel az NB 90° TN LC cellát (sárga drótok) a két polárszűrő közé, és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan!
- Ügyeljen arra, hogy a lézersugár a cella közepén haladjon át, mert csak itt tudjuk a ráadott feszültséggel orientálni a molekulákat!
Forgassa körbe 5-10°-os lépésekben az LC cellát! Mérje meg, foglalja táblázatba és ábrázolja az áthaladó fény intenzitását a forgatás  szögének függvényében!
szögének függvényében!
- Miért változik a fényintenzitás?
5. Állítsa be úgy az LC cellát, hogy az intenzitás minimális legyen (NB mód)! Kapcsoljon a cellára 100 Hz-es négyszögjelet, és változtassa a jel (effektív) feszültségét 0-tól 7 V-ig!
- Figyeljen arra, hogy a fontos, érdekes pontoknál megfelelően kis lépésekben változtassa a feszültséget!
Mérje meg, foglalja táblázatba és ábrázolja az NB 90° TN LC cella elektro-optikai kapcsolási görbéjét (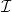 az
az  függvényében)!
függvényében)!
Határozza meg a 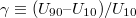 kapcsolási meredekséget és az
kapcsolási meredekséget és az 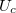 kritikus feszültséget!
kritikus feszültséget! 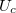 meghatározásánál vegye figyelembe, hogy
meghatározásánál vegye figyelembe, hogy 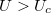 feszültségnél az
feszültségnél az 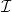 fényintenzitás
fényintenzitás  monoton növekvő függvénye!
monoton növekvő függvénye!
6. Párhuzamos polarizátor állás mellett forgassa a NB 90° TN LC cellát olyan pozícióba, melyben maximális az intenzitás. Mérje meg a cellára kapcsolt 100 Hz-es négyszögjel effektív feszültségének függvényében az intenzitás változását a 0-7 V tartományban!
- Értelmezze a megfigyeléseket!
A párhuzamosan rendezett LC cella vizsgálata
7. Cserélje ki az NB 90° TN LC cellát a párhuzamosan rendezett cellával (narancssárga drótok), és állítsa be a fénysugárra merőlegesen a polárszűrőkhöz hasonlóan!
- A lézersugár ismét a cella közepén haladjon át! Egyelőre ne kapcsoljon feszültséget a cellára (
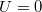 )!
)!
Állítsa be a 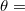 45°-os elrendezést! Ehhez állítsa az analizátort a polarizátorral merőleges állásba (forgassa el 90°-kal), majd forgassa a párhuzamosan rendezett LC cellát addig, amíg az átmenő fény intenzitása el nem éri a maximális értékét (
45°-os elrendezést! Ehhez állítsa az analizátort a polarizátorral merőleges állásba (forgassa el 90°-kal), majd forgassa a párhuzamosan rendezett LC cellát addig, amíg az átmenő fény intenzitása el nem éri a maximális értékét (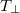 )! Ez a helyzet valósítja meg a
)! Ez a helyzet valósítja meg a 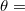 45°-os konfigurációt. Jegyezze fel a
45°-os konfigurációt. Jegyezze fel a 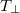 -sel arányos intenzitásértékét! Ezután mérje meg ugyanebben a
-sel arányos intenzitásértékét! Ezután mérje meg ugyanebben a 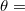 45°-os állásban az áteresztő képességet abban az esetben is, ha az analizátor és a polarizátor polarizációs iránya párhuzamos (
45°-os állásban az áteresztő képességet abban az esetben is, ha az analizátor és a polarizátor polarizációs iránya párhuzamos (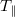 )!
)!
Tudjuk, hogy a lézerfény hullámhossza 650 nm, az LC réteg vastagsága  = 7,7 μm és hogy
= 7,7 μm és hogy 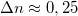 . Felhasználva
. Felhasználva 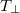 és
és 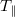 az előzőek szerint megmért arányát, számítsa ki a
az előzőek szerint megmért arányát, számítsa ki a 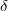 fáziskülönbség és a
fáziskülönbség és a 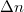 optikai anizotrópia pontos értékét az adott LC cellára,
optikai anizotrópia pontos értékét az adott LC cellára, 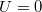 esetében!
esetében!
8. Az előzőekhez hasonlóan, továbbra is a 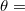 45°-os konfigurációban mérjen! Kapcsoljon 100 Hz-es négyszögjelet a cellára és változtassa a feszültség (effektív) értékét 0-tól 7 V-ig! Mérje meg, foglalja táblázatba és ábrázolja a párhuzamos cella elektro-optikai kapcsolási görbéjét az analizátor és a polarizátor párhuzamos állásánál (
45°-os konfigurációban mérjen! Kapcsoljon 100 Hz-es négyszögjelet a cellára és változtassa a feszültség (effektív) értékét 0-tól 7 V-ig! Mérje meg, foglalja táblázatba és ábrázolja a párhuzamos cella elektro-optikai kapcsolási görbéjét az analizátor és a polarizátor párhuzamos állásánál (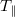 )!
)!
- A függvény szélsőértékeinek közelében vegye fel sűrűbben a pontokat (különösen a 0,5-4,0 V feszültségtartományban)!
Az elektro-optikai kapcsolási görbéből határozza meg a fázistolás mértékét 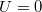 feszültségnél!
feszültségnél!
- Vesse össze az eredményt a 7. feladatban kapott eredménnyel!
Az elektro-optikai kapcsolási görbéből határozza meg azokat az 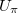 feszültségeket, amelyeknél az LC cellában a fázistolás
feszültségeket, amelyeknél az LC cellában a fázistolás 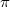 (180°)$!
(180°)$!
- Ne felejtse el, hogy
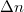 (és így
(és így 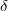 is) az
is) az  feszültség csökkenő függvénye!
feszültség csökkenő függvénye!
Az elektro-optikai kapcsolási görbéből határozza meg azt a minimális  feszültséget, ahol a cellából kilépő fény cirkulárisan polarizált!
feszültséget, ahol a cellából kilépő fény cirkulárisan polarizált!
- A fény akkor válik cirkulárisan polarizálttá, ha a fázistolás
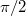 páratlan többszöröse.
páratlan többszöröse.
A mérés végén ne felejtse el kikapcsolni a lézert, és kivenni az elemet a fotodetektorból!