Harmonikus rezgések vizsgálata

A mérés célja:

• elmélyíteni a hallgatók harmonikus rezgésekről szóló ismereteit,
• megtapasztalni a mechanikai és az elektromos rezgések közötti analógiát,
• megismerkedni a váltóáramú mérésekkel és a komplex jelöléssel,
• valamint egyszerű szűrőkapcsolások tulajdonságaival

Ennek érdekében:

• a mechanikai rezgések leírásán keresztül áttekintjük a harmonikus rezgések elméletét,
• megismerjük a különböző áramköri elemek váltóáramú viselkedését,
• áttekintjük a komlex jelölést
• megismerkedünk néhány egyszerű szűrőelrendezéssel,
• megvizsgáljuk a mechanikai rezgéseket,
• méréseket végzünk alul- és felüláteresztő szűrőkkel,
• megvizsgáljuk a feszültségviszonyokat soros RLC körökben,
• megfigyeljük az analógiát a soros RLC és a mechanikai rezgések között.

Elméleti összefoglaló

A harmonikus rezgés alapvető fizikai jelenség. Vibrációk, oszcillációk harmonikus rezgéssel modellezhetők, ha az amplitúdók elég kicsinyek. A harmonikus mozgás differenciálegyenlete nem csupán a klasszikus fizikában (mechanika, villamosságtan), de a kvantumfizikában, a szilárdtestfizikában és az optikában is gyakran előfordul. A harmonikus rezgés tulajdonságait a mechanikai rezgések példáján keresztül tárgyaljuk, majd megmutatjuk a soros RLC körökben megfigyelhető elektromos rezgések és a mechanikai rezgések közötti analógiát. Végül pedig bevezetjük a komplex jelölést és megvizsgálunk néhány egyszerű szűrőelrendezést.

Harmonikus mechanikai rezgések leírása

Csillapítatlan mechanikai rezgések

Ha egy $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegű anyagi pontra a kitéréssel arányos, rugalmas erő hat, akkor a mozgásegyenlet

$\[ma=-Dx\]$

alakú, ahol $\setbox0\hbox{$D$}% \message{//depth:\the\dp0//}% \box0%$ a rugóállandó, $\setbox0\hbox{$x$}% \message{//depth:\the\dp0//}% \box0%$ a tömegpont kitérése az egyensúlyi helyzetből, $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ a tömeg, és $\setbox0\hbox{$a$}% \message{//depth:\the\dp0//}% \box0%$ a gyorsulás. A mozgásegyenlet megoldása

$\[x(t)=A\sin(\omega_0 t+\alpha)\]$

ahol $\setbox0\hbox{$A$}% \message{//depth:\the\dp0//}% \box0%$ a (kitérési) amplitúdó, $\setbox0\hbox{$\alpha$}% \message{//depth:\the\dp0//}% \box0%$ a $\setbox0\hbox{$t=0$}% \message{//depth:\the\dp0//}% \box0%$ időpillanathoz tartozó fázis (mindkettőt a kezdeti feltételek határozzák meg),

$\[\omega_0=\sqrt{\frac{D}{m}}\]$

a csillapítatlan rezgő rendszer körfrekvenciája. (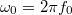$\setbox0\hbox{$\omega_0=2\pi f_0$}% \message{//depth:\the\dp0//}% \box0%$, ahol $\setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0%$ a megfelelő frekvencia.)

A harmonikus rezgőmozgás sebessége

$\[v(t)=\frac{\text{d} x}{\text{d} t}=A\omega_0\cos(\omega_0 t+\alpha)\]$

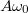ahol $\setbox0\hbox{$A\omega_0$}% \message{//depth:\the\dp0//}% \box0%$ a maximális sebesség, az ún. sebességamplitúdó.

Csillapodó rezgések

A csillapodást okozó erők gyakran (jó közelítéssel) a sebességgel arányosak: 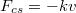$\setbox0\hbox{$F_{cs}=-kv$}% \message{//depth:\the\dp0//}% \box0%$, ahol $\setbox0\hbox{$k$}% \message{//depth:\the\dp0//}% \box0%$ a csillapítás erősségére jellemző mennyiség. Ekkor a tömegpont mozgásegyenlete:

$\[ma=-Dx-kv\]$

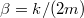ami a $\setbox0\hbox{$\beta=k/(2m)$}% \message{//depth:\the\dp0//}% \box0%$ csillapítási tényező bevezetésével és $\setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%$ definíciójának felhasználásával az alábbi alakra hozható:

$\[\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=0\]$

A differenciálegyenlet megoldása 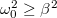$\setbox0\hbox{$\omega_0^2\geq\beta^2$}% \message{//depth:\the\dp0//}% \box0%$ esetén időben csökkenő amplitúdójú lengéseket eredményez:

$\[x(t)=Ae^{-\beta t}\sin(\omega' t+\alpha)\]$

A rezgés körfrekvenciája

$\[\omega'=\sqrt{\omega_0^2-\beta^2}\]$

Az amplitúdóváltozás jellemzésére különböző mennyiségeket használnak. A csillapodási hányados két, azonos irányban egymás után következő amplitúdó hányadosa

$\[K=\frac{x_n}{x_{n+1} }=e^{\beta T}\]$

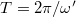ahol $\setbox0\hbox{$T=2\pi/\omega'$}% \message{//depth:\the\dp0//}% \box0%$. Használatos még a K csillapodási hányados logaritmusa, az ún. logaritmikus dekrementum is:

$\[\Lambda=\ln K=\beta T\]$

Kényszerrezgések

Egy $\setbox0\hbox{$m$}% \message{//depth:\the\dp0//}% \box0%$ tömegre pl. motor és excenter segítségével időben periodikusan változó erőt alkalmazva egy átmeneti időszak után időben állandósult rezgés alakul ki, melynek frekvenciája megegyezik a kényszerítő erő frekvenciájával, míg amplitúdója függ az erőtől, a rugóállandótól, a tömegtől, a csillapítástól valamint a gerjesztő frekvenciától. Az anyagi pont mozgásegyenlete ekkor:

$\[ma=-Dx-kv+F_0\sin(\omega t)\]$

A korábban bevezetett jelöléseket alkalmazva másodrendű lineáris, inhomogén differenciálegyenletet kapunk:

$\[\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2 x=\frac{F_0}{m}\sin(\omega t)\]$

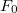ahol $\setbox0\hbox{$F_0$}% \message{//depth:\the\dp0//}% \box0%$ a kényszererő maximális értéke. Az egyenlet megoldása:

$\[x(t)=A_0e^{-\beta t}\sin(\omega' t+\alpha)+\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} }\sin(\omega t+\varphi),\]$

melynek második tagja írja le az állandósult állapotot. Az állandósult állapot amplitúdója:

$\[A(\omega)=\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2} },\]$

melynek maximuma van az

$\[\omega_{max}=\sqrt{\omega_0^2-2\beta^2}\]$

körfrekvenciánál. A $\setbox0\hbox{$\varphi$}% \message{//depth:\the\dp0//}% \box0%$ fázisállandó nem az időmérés kezdetétől függ, hanem a kényszerítő erő fázisától való eltérés, ennek tangense:

$\[\text{tg}\varphi=\frac{2\beta\omega}{\omega_0^2-\omega^2}.\]$

Az amplitúdóhoz hasonlóan megadhatjuk a sebességamplitúdó kifejezését is:

$\[A\omega=\frac{F_0\omega}{m\sqrt{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}}\]$

melynek maximuma – ellentétben a kitérési amplitúdó maximumával – éppen $\setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%$-nál van, ahol

$\[A\omega_0=\frac{F_0}{2m\beta}.\]$

A kényszerrezgés energiaviszonyainak jellemezésére az egy periódus alatt disszipált energia 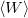$\setbox0\hbox{$\langle W\rangle$}% \message{//depth:\the\dp0//}% \box0%$ és a rendszerben tárolt átlagos energia 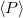$\setbox0\hbox{$\langle P\rangle$}% \message{//depth:\the\dp0//}% \box0%$ hányadosával arányos jósági tényezőt használjuk

$\[Q=2\pi\frac{\langle W\rangle}{T\langle P\rangle}\approx\frac{\omega_0}{2\beta}\]$

Váltakozó áramú kapcsolások

Áramköri elemek áram- és feszültségviszonyai

Ohmos ellenállás

Az ellenálláson eső feszültséget az

$\[u(t)=R i(t)\]$

összefüggés írja le. Szinuszos gerjesztés [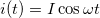$\setbox0\hbox{$i(t)=I\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%$] esetén

$\[u(t) = R I \cos\omega t,\]$

azaz az ohmos ellenálláson a feszültség és az áram azonos fázisban van.

Tekercs

A tekercsben indukálódó feszültséget az

$\[u(t) = L \frac{{\rm d}i(t)}{{\rm d}t}\]$

egyenlet írja le. Szinuszos gerjesztés [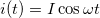$\setbox0\hbox{$i(t)=I\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%$] esetén

$\[u(t) = -L \omega I \sin\omega t = L \omega I \cos( \omega t + 90^\circ),\]$

tehát a tekercsben fellépő feszültség 90°-ot siet az átfolyó áramhoz képest.

Kondenzátor

A kondenzátoron átfolyó áram időfüggését az alábbi egyenlet írja le:

$\[i(t) = C \frac{{\rm d}u(t)}{{\rm d}t}.\]$

Szinuszos gerjesztés [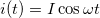$\setbox0\hbox{$i(t)=I\cos\omega t$}% \message{//depth:\the\dp0//}% \box0%$] esetén:

$\[u(t) = \frac{I}{C\omega}\sin\omega t = \frac{I}{C\omega}\cos(\omega t - 90^\circ),\]$

azaz a kondenzátor feszültsége 90°-kal késik az áramhoz képest.

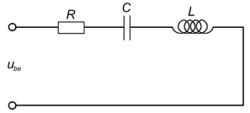
Soros rezgőkör

Kondenzátor és tekercs soros kapcsolását (a veszteségeket soros ellenállással figyelembe véve) soros rezgőkörnek nevezik (6. ábra). Az alábbiakban láthatjuk, hogy ez az áramkör a korábban ismertetett kényszerrezgés elektromos megfelelője, amennyiben a tömegpont kitérését megfeleltetjük a kondenzátor töltésének, a rugóállandót a kondenzátor kapacitásának, a tömegpont tömegét a tekercs induktivitásának és a csillapítást az ellenállásnak. Ha az RLC körben a kondenzátort feltöltenénk, majd a bemenetet rövidre zárnánk, akkor egy csillapodó rezgést figyelhetnénk meg. A nagy frekvencia és a gyors csillapodás miatt azonban ezt nehezebb megfigyelni, mint egy kitérített, és magára hagyott mechanikai rezgő rendszert. Ha a bemenetre szinuszos gerjesztő feszültséget kapcsolunk, akkor viszont a kényszerrezgéssel teljesen analóg viselkedést figyelhetünk meg.

Viszgáljuk meg a rezgőkör differenciálegyenletét a kondenzátor időfüggő töltésére (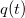$\setbox0\hbox{$q(t)$}% \message{//depth:\the\dp0//}% \box0%$) felírva, amikor a rezgőkörre 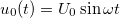$\setbox0\hbox{$u_0(t)=U_0\sin\omega t$}% \message{//depth:\the\dp0//}% \box0%$ feszültséget kapcsolunk:

$\[u_{\rm C}=q(t)/C\]$

$\[i(t)=\dot{q}(t)\]$

$\[u_{\rm R}=Ri(t)=R\dot{q}(t)\]$

$\[u_{\rm L}=L\dot{i}(t)=L\ddot{q}(t)\]$

$\[L\ddot{q}(t)+R\dot{q}(t)+q(t)/C=U_0\sin\omega t\]$

$\[\ddot{q}(t)+\frac{R}{L}\dot{q}(t)+\frac{1}{LC}q(t)=\frac{U_0}{L}\sin\omega t.\]$

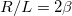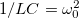Vegyük észre, hogy ez a differenciálegyenlet $\setbox0\hbox{$R/L=2\beta$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$1/LC=\omega_0^2$}% \message{//depth:\the\dp0//}% \box0%$ jelöléssel a kényszerrezgést leíró differenciálegyenlettel teljesen analóg egyenletet eredményez. Ennek következtében az általános megoldás is teljesen analóg: traniens és állandósult tagokat tartalmaz.

Esetünkben a tranziens tag hamar elhal, és az állandósult tagot tanulmányozhatjuk. Az amplitúdó itt a kondenzátor töltése, de számunkra sokkal érdekesebb ennek deriváltja, a körben folyó áramerősség. Ez tehát az analógia alapján a mechanikai rezgés sebességrezonanciájával egyezik meg:

$\[I(\omega)=\frac{U_0}{L\sqrt{\left(\omega^2-\omega_0^2\right)^2+4\beta^2\omega^2}}.\]$

Ha behelyettesítjük $\setbox0\hbox{$\beta$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%$ értékét, akkor

$\[I(\omega)=\frac{U_0}{\sqrt{(\omega L-1/\omega C)^2+R^2}}.\]$

Látható, hogy a rezgőkörben folyó áramnak 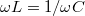$\setbox0\hbox{$\omega L = 1/\omega C$}% \message{//depth:\the\dp0//}% \box0%$ esetén az

$\[\omega_0 = \frac{1}{\sqrt{LC}}\]$

körfrekvencián maximuma van. A jelenséget rezonanciának, $\setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%$-t rezonancia-körfrekvenciának hívják. Ezen a körfrekvencián áramrezonancia alakul ki.

Ez az áram – kis veszteségi ellenállást feltételezve – igen nagy feszültségeket hozhat létre a kondenzátoron és a tekercsen. Azonban ezek a feszültségek egymáshoz viszonyítva 180°-os fázisban vannak, abszolút értékük pedig megegyezik (hiszen azonos áram folyik át rajtuk), így egymást kiegyenlítik.

Megjegyzés: A kondenzátoron és a tekercsen eső feszültségnek nem pontosan az $\setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%$ rezonanciafrekvencián van maximuma - hasonlóan a mechanikai kényszerrezgés amplitúdórezonanciájához.

Komplex jelölés

1. ábra

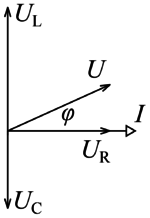
Szinuszos gerjesztés esetén, állandósult állapotban minden áram- és feszültségfüggvény azonos $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ körfrekvenciával változik. Az egymáshoz képesti fáziskülönbségeket ilyenkor fazorábrával szemléltethetjük. Az 1. ábrán egy soros RLC-kör (részletesen lásd később) fazorábrája látható. Az áram - a soros kapcsolás miatt - mindhárom elemen ugyanakkora, a feszültségek pedig ehhez viszonyítva sietnek, fázisban vannak, illetve késnek.

Az áramkörre kapcsolt feszültség a három, sorbakapcsolt feszültséget jelölő fazor vektori eredője.

A fazorokat felfoghatjuk komlex számokként is. Így az egyes áram és feszültségjeleket egy-egy komplex szám jelöli. A fazorokhoz hasonlóan a komplex szám abszolút értéke a jel nagyságát (csúcsértékét), a komplex szám arkusza pedig a jel (a kiválasztott fázishelyzethez viszonyított) fázisát adja meg.

Figyelem! Mivel a villamos hálózatoknál 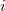$\setbox0\hbox{$i$}% \message{//depth:\the\dp0//}% \box0%$ az áram pillanatértékét jelöli, a komplex egység szokásos jelölése itt $\setbox0\hbox{$j$}% \message{//depth:\the\dp0//}% \box0%$ !

Az 1. ábrán látható fazorábrán szereplő jeleknek megfelelő komplex mennyiségek:

$\[\mathbf{I}=I\]$

$\[\mathbf{U_{\rm R}}=U_{\rm R}=RI\]$

$\[\mathbf{U_{\rm L}}=jU_{\rm L}=j\omega LI\]$

$\[\mathbf{U_{\rm C}}=-jU_{\rm C}=I/j\omega C\]$

Ekkor az eredő (komplex) feszültséget nem csak megszerkeszthetjük, hanem egyszerű komplex algebrával ki is számolhatjuk:

$\[\mathbf{U} = \mathbf{U_{\rm R}}+\mathbf{U_{\rm L}}+\mathbf{U_{\rm C}}= RI + j\omega LI + I/j\omega C\]$

Az eredő feszültség nagysága (csúcsértéke) a komplex érték abszolút értéke:

$\[U=|\mathbf{U}|=\sqrt{R^2+(\omega L-1/\omega C)^2}I=ZI,\]$

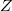ahol $\setbox0\hbox{$Z$}% \message{//depth:\the\dp0//}% \box0%$ az eredő ellenállás.

Az eredő feszültség fázisa a komplex feszültség arkusza:

$\[\varphi=\arccos\frac{R}{Z}.\]$

A komplex áram és feszültség alapján azonban közvetlenül is fel tudjuk írni az áram és a feszültség időfüggvényét:

$\[i(t)=\rm{Re}\left(\mathbf{I}e^{j\omega t}\right)=I\cos \omega t\]$

$\[u(t)=\rm{Re}\left(\mathbf{U}e^{j\omega t}\right)=U\cos(\omega t+\varphi)=ZI\cos(\omega t+\varphi)\]$

2. ábra

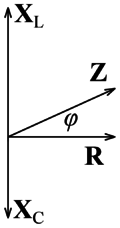
Ha az 1. ábrán látható fazorokat leíró komplex feszültségeket elosztjuk az áramerősség nagyságával, akkor ellenállás dimenziójú komplex mennyiségeket kapunk:

$\[\frac{\mathbf{U_{\rm R}}}{I}=\mathbf{R}=R\]$

$\[\frac{\mathbf{U_{\rm L}}}{I}=\mathbf{X_{\rm L}}=j\omega L\]$

$\[\frac{\mathbf{U_{\rm C}}}{I}=\mathbf{X_{\rm C}}=1/j\omega C\]$

$\[\frac{\mathbf{U}}{I}=\mathbf{Z}\]$

A komplex ellenállásokkal ugyanúgy számolhatunk egy váltóáramú körben, mint az ohmos ellenállásokkal egyenáramú hálózatok esetében.

A mi esetünkben a soros kapcsolás miatt az eredő (komplex) ellenállás az egyes (komplex) ellenállások összege:

$\[\mathbf{Z}=\mathbf{R}+\mathbf{X_{\rm L}}+\mathbf{X_{\rm C}}.\]$

A komplex jelölésmóddal bármely áramköri elem leírása olyan, mintha egy ohmos ellenállás lenne:

$\[\mathbf{U_{\rm R}}=\mathbf{R}\mathbf{I}\]$

$\[\mathbf{U_{\rm L}}=\mathbf{X_{\rm L}}\mathbf{I}\]$

$\[\mathbf{U_{\rm C}}=\mathbf{X_{\rm C}}\mathbf{I}\]$

$\[\mathbf{U}=\mathbf{Z}\mathbf{I}\]$

A komplex ellenállás abszolút értéke a skalár ellenállás értéket adja, míg arkusza azt mutatja meg, hogy az adott áramköri elem mennyivel tolja el a fázist.

Szűrő áramkörök

Szűrők segítségével egy különböző frekvenciájú rezgésekből álló elektromos jelből ki lehet szűrni bizonyos frekvenciatartományokat. Ezen a mérésen csak RC alul- és felüláteresztő szűrőket fog mérni, de itt néhány más kapcsolást is bemutatunk.

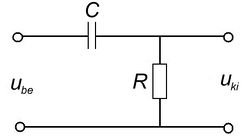
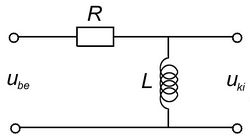
Aluláteresztő szűrők

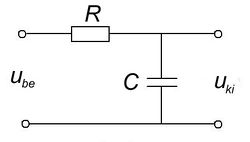
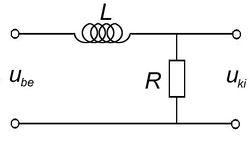
A 3/a és 3/b ábrákon látható kapcsolások kimenő feszültségeit a komplex jelölésmód segítségével könnyen felírhatjuk. (Egyszerűen az egyenáramú áramkörökben jól ismert 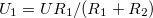$\setbox0\hbox{$U_1=UR_1/(R_1+R_2)$}% \message{//depth:\the\dp0//}% \box0%$ feszültségosztó képletet használjuk, de itt komplex ellenállásokkal.) A vastag betűs mennyiségek komplex változók, $\setbox0\hbox{$j$}% \message{//depth:\the\dp0//}% \box0%$ a képzetes egység. Ugyanakkor mérni csak valós mennyiségeket lehet, azaz a komplex mennyiségek abszolút értékét!

3/a ábra	3/b ábra
$\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{1/j\omega C}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega RC} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega RC}\right|=\frac{1}{\sqrt{1+(\omega RC)^2}} \end{array} \]$	$\[ \begin{array}{rcl} \mathbf{U}_{\rm ki} & = & \mathbf{U}_{\rm be} \frac{R}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{\rm ki}}{\mathbf{U}_{\rm be}} & = & \frac{1}{1 + j\omega L/R} \\ \\ \frac{U_{\rm ki}}{U_{\rm be}} & = & \left|\frac{1}{1 + j\omega L/R}\right|=\frac{1}{\sqrt{1+(\omega L/R)^2}} \end{array} \]$

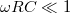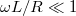A kimeneti és bemeneti feszültségek hányadosa, a hálózatra jellemző, frekvenciafüggő kifejezés. A két kifejezés formailag azonos, tehát a két kapcsolás azonos jellegű viselkedést mutat. 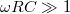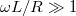Ameddig $\setbox0\hbox{$\omega RC \ll 1$}% \message{//depth:\the\dp0//}% \box0%$ vagy $\setbox0\hbox{$\omega L/R \ll 1$}% \message{//depth:\the\dp0//}% \box0%$, a kifejezések értéke 1; ha $\setbox0\hbox{$\omega RC \gg 1$}% \message{//depth:\the\dp0//}% \box0%$ vagy $\setbox0\hbox{$\omega L/R \gg 1$}% \message{//depth:\the\dp0//}% \box0%$, a hányados értéke 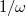$\setbox0\hbox{$1/\omega$}% \message{//depth:\the\dp0//}% \box0%$ szerint csökken. Ez azt jelenti, hogy adott $\setbox0\hbox{$R$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$C$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$L$}% \message{//depth:\the\dp0//}% \box0%$ esetén az alacsony frekvenciájú jelek csillapítás nélkül jelennek meg a kimeneten, míg magasabb frekvenciákon a kimenő feszültség egyre kisebb. Ezeket a kapcsolásokat aluláteresztő szűrőknek nevezik.

Felüláteresztő szűrő

A 4/a és a 4/b ábrákon látható kapcsolásokat leíró egyenletek az előző pontban követett eljárás alapján az alábbiak szerint alakulnak.

4/a ábra	4/b ábra
$\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{R}{R + 1/j\omega C} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + 1/j\omega RC} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + 1/j\omega RC}\right|=\frac{1}{\sqrt{1+(1/\omega RC)^2}} \end{array} \]$	$\[ \begin{array}{rcl} \mathbf{U}_{{\rm ki}} & = & \mathbf{U}_{{\rm be}} \frac{j\omega L}{R + j\omega L} \\ \\ \frac{\mathbf{U}_{{\rm ki}}}{\mathbf{U}_{{\rm be}}} & = & \frac{1}{1 + R/j\omega L} \\ \\ \frac{U_{{\rm ki}}}{U_{{\rm be}}} & = & \left|\frac{1}{1 + R/j\omega L}\right|=\frac{1}{\sqrt{1+(R/\omega L)^2}} \end{array} \]$

A kifejezésekből jól látszik, hogy a kapcsolások a kisfrekvenciás jeleket nem engedik a kimenetre, míg a nagyfrekvenciás jelek csillapítás nélkül jelennek meg a kimeneti pontokon. Ezek felüláteresztő szűrők.

5. ábra

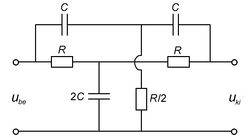
Sávzáró és sáváteresztő szűrő

Alul és felüláteresztő szűrők egymás után kapcsolásával és az áteresztési tartományok helyes megválasztásával előállítható olyan szűrő, amelyik csak egy meghatározott tartományban csillapítja a jelet. Az ilyen kapcsolást nevezik sávzáró szűrőnek. Ennek egy realizálása a 5. ábrán látható kettős T szűrő.

A kapcsolás részletes elemzése nélkül is megállapítható, hogy alacsony frekvenciákon a hosszági ellenállásokon, magas frekvenciákon a hosszági kondenzátorokon jut jel a kimenetre.

Ehhez hasonlóan alul- és felüláteresztő szűrőkből összeállítható olyan kapcsolás is, amely csak egy meghatározott tartományban engedi át a jeleket. Ezek a sáváteresztő szűrők.

Az eddig ismertetett szűrőkapcsolások passzív elemekből állnak, jellemzőjük, hogy a kimeneti jel az áteresztési tartományokban sem nagyobb a bemenetinél. Aktív eszközökkel (pl. műveleti erősítő) készíthető olyan szűrő, amelyik egyben a jel erősítését is elvégzi az áteresztési tartományban.

6. ábra

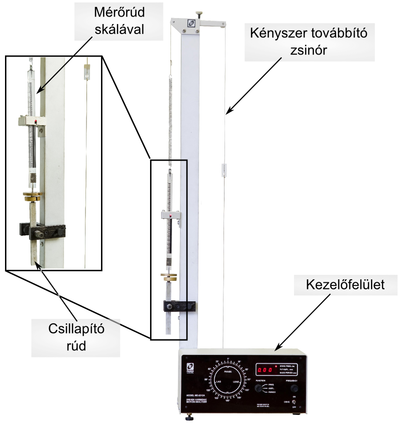
A kísérleti berendezés leírása

1. ábra

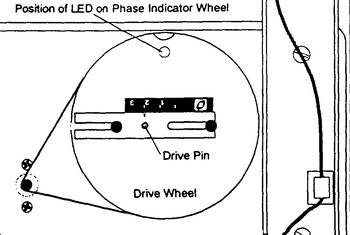
A kísérleti berendezés az 1. ábrán látható. Az alul elhelyezkedő elektronikai egység hátsó lapján található a kényszererőt létrehozó excenter. A kényszererő amplitúdója az amplitúdórúd helyzetének változtatásával szabályozható, ami a kényszert kifejtő zsinór rögzítési pontja és az excenter középpontja közötti távolságot befolyásolja (2. ábra). A kényszert továbbító zsinór a tartóoszlop tetején található két csiga vájatain áthaladva egy hurokkal kapcsolódik a vizsgálandó rugó egyik végéhez. A másik véghez a skálával ellátott mérőrúd és a hozzá erősített ún. csillapító rúd csatlakozik. E két rúd alkotja a rezgőmozgást végző „alaptömeget”, melynek értéke 50 g.

A mérőkészlethez tartozik két 50 g tömegű rézkorong is. A korongokat a mérőrudat és csillapitórudat összekötő csavarmenetre lehet felerősíteni. A tartóoszlop középmagasságánál látható a rúdvezető, melyben optikai érzékelők vannak. A mérőrudat a rúdvezető téglalap alakú nyílásán kell átvezetni.

Helyes beállítás esetén a rezgés csillapodása – melyet a légellenállás ill. a berendezés egyes elemei között fellépő súrlódás okoz – igen kicsi. Ezért a csillapítás változtatása (növelése) céljából a tartórúdra egy olyan mágnespárt szerelhetünk fel, melynek pofái között a távolság változtatható. Ezen mágnespofák között mozog az alumíniumból készült csillapítórúd. A mágneses tér hatására a mozgó fémrúdban örvényáramok keletkeznek, melyek Joule-hőjének disszipációja okozza a rendszer csillapodását. A mágnespofák közötti távolság csökkentésével a mágneses térerősség növelhető, azaz a disszipáció, vagyis a csillapítás fokozható.

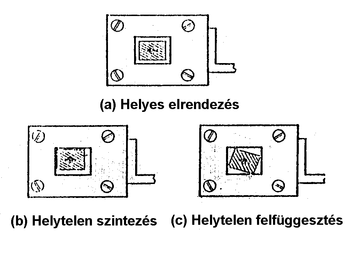
Beállítás

• Ha a készülék jól van beállítva, a mérőrúd úgy függ, hogy egyik oldala sem ér hozzá a rúdvezető nyílásának falához (3. ábra). A nem jó a beállítás a 3. ábrán látható „b” vagy „c” esetben fordul elő. A „b” esetet az elektronika doboz változtatható magasságú lábainak megfelelő állításával korrigálhatjuk (vízszintezés). A „c” eset a mérőrúd felfüggesztésével (elcsavarásával)javítható.
• A fázis és amplitúdó pontos méréséhez úgy kell felfüggeszteni a mérőrudat, hogy egyensúlyi helyzetben középvonala egybeessen a rúdvezető optikai érzékelőjével. Ennek beállításához:
  • Kapcsolja be az elektronika doboz hátoldalán levő kapcsolót. Figyelje a rúdvezető LED-et. Ha a mérőrúd középvonala (8,5 cm) feljebb van, mint a rúdvezető felső éle, akkor a LED kialszik. Ha a középvonal lejjebb került, akkor a LED kigyullad.
  • Mozgassa úgy a mérőrudat fel és le, hogy a középvonala áthaladjon a rúdvezetőn. Közben figyelje a FÁZIS kijelzést. Amikor a mérőrúd középvonala lefelé halad keresztül a rúdvezetőn, egy LED villog a fázisskálán. Annyira fordítsa el a kényszerkereket, hogy a fázist jelző LED éppen 0° fázishelyzetet mutasson.
  • Most pontosítsa a zsinór hosszát. Ez a zsinóron található plasztikcsattal állítható. Finom állítások a tartóoszlop tetején levő csavarral végezhetők. A zsinórhossz akkor megfelelő, ha egészen kicsi oszcillációknál a fázis LED ki-be kapcsol.

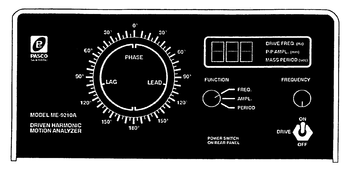
Az elektronika doboz a 4. ábrán látható. Az elülső lapon található a DRIVE kapcsoló. Ezzel indítható a motor, mely a kényszer kereket forgatja. A FREQUENCY gombbal változtatható a kényszer frekvenciája. Óramutató járásával megegyezően forgatva növeli a frekvenciát. A FUNCTION kapcsoló határozza meg azt, hogy az alábbi három változóból melyiket írja ki a digitális kijelző. (A kijelző jobb oldalán egy LED mutatja, hogy melyik változó értéket olvashatjuk le.)

• FREQ. – A kényszerkerék frekvenciája (Hz)
• AMPL. – A mérőrúd csúcstól-csúcsig amplitúdója (ez az amplitúdó kétszerese) (mm)
• PERIOD – A mérőrúd egy teljes rezgésének periódusideje (s).

2. ábra

3. ábra

4. ábra

Mérési feladatok

A méréshez rendelkezésre álló eszközök

• A mérés elvégzéséhez és a mérési napló elkészítéséhez a dőlt betűs részekben adunk segítséget.

1. A rugóállandó mérése

Állítsa be a zsinór hosszát úgy, hogy a mérőrúd 17 cm-es jele a rúdvezető alsó szélével egy vonalba essék! Erősítse az egyik 50 g-os rézsúlyt a mérőrúd és a csillapítórúd közé! Mérje le a rugó sztatikus megnyúlását! Ezután helyezze fel a második rézsúlyt is, és mérje meg az újabb megnyúlást! Számítsa ki a rugó rugóállandóját!

2. Csillapítatlan rendszer lengésideje

Szabályozza be a készüléket!

• Nagyon fontos, hogy a mérőrúd ne érjen a rúdvezető egyik falához se (lásd az előző pontban)!

Ehhez a méréshez szerelje le a csillapító mágnespofákat! A funkciókapcsolót állítsa periódusidőmérésre (PERIOD). Húzza a mérőrudat kb. 5 cm-rel az egyensúlyi helyzete alá, és engedje el! A digitális kijelző ekkor a rezgés periódusidejét (s) mutatja. A mérést üres mérőrúddal, majd 50 és 100 g-os terhelésekkel is végezze el!

• Az eredményeket foglalja táblázatba és vesse össze az elmélet alapján kiszámolt értékekkel!

3. Kényszerrezgés amplitúdójának és sebességamplitúdójának vizsgálata a kényszerítő frekvencia függvényében

A méréseket két különböző csillapítás esetén, mérőrúd + 50 g tömeggel végezze el! Szerelje vissza a csillapító mágnespofákat! A kis csillapításhoz a csillapító mágnespofákat egymástól a lehető legtávolabb állítsa be! A nagy csillapításhoz tekerje a mágnespofákat a lehető legközelebb, de csak annyira, hogy ne érjenek hozzá a csillapítórúdhoz! Ekkor mérje meg és jegyezze fel a mágnespofák távolságát!

Gondosan állítsa be a mérőrúd helyzetét úgy, hogy már egészen kis kitéréseknél villogjon a digitális kijelző (beállítás)! A funkciókapcsolót állítsa frekvenciamérésre (FREQ.) és a DRIVE kapcsolóval indítsa el a kényszerrezgést! A frekvenciaszabályozó gombbal lassan (fokozatosan) növelje a frekvenciát, és időről-időre váltson át az amplitúdómérésre (AMPL.)!

• Itt a kijelző mm-ben megadja a csúcstól-csúcsig amplitúdót – ez az amplitúdó kétszerese.
• Figyelje eközben a fázisállandót jelző LED értékét is! Amikor a kényszerítő frekvencia megegyezik az $\setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0%$ sajátfrekvenciával, a fázisszög 90°.

Keresse meg az 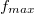$\setbox0\hbox{$f_{max}$}% \message{//depth:\the\dp0//}% \box0%$ rezonanciafrekvenciát, ahol az amplitúdó maximális!

• A rezonanciafrekvencia – különösen nagy csillapítás esetében – eltér a sajátfrekvenciától.
• Amennyiben a rezgések amplitúdója túl nagy vagy túl kicsi lenne, úgy kapcsolja ki a készüléket és csökkentse, illetve növelje a kényszererő amplitúdóját, majd ellenőrizze a kitérést a rezonanciafrekvenciánál!

Amennyiben mindent rendben talál, vegye fel táblázatosan a rezonanciafrekvenciánál 1 Hz-cel kisebb és 1 Hz-cel nagyobb frekvenciák közötti intervallumban 0,1 Hz-enként (és a rezonancia frekvencia közelében ennél sűrűbben is) a kitérési amplitúdókat! Ábrázolja a különböző csillapítással felvett görbéket közös diagrammon! Adja meg minden esetben 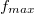$\setbox0\hbox{$f_{max}$}% \message{//depth:\the\dp0//}% \box0%$ értékét!

A korábban megmért görbék valamennyi pontjánál (a kitérési amplitúdó és frekvencia ismeretében) számítsa ki a sebeségamplitúdó 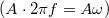$\setbox0\hbox{$(A\cdot 2\pi f=A\omega)$}% \message{//depth:\the\dp0//}% \box0%$ értékeket! Foglalja táblázatba és ábrázolja diagrammon a sebességamplitúdó – körfrekvencia görbéket!

• A különböző csillapítással felvett görbéket most is közös diagrammon ábrázolja!

4. Csillapítási tényező és jósági tényező meghatározása

A csillapítási tényező kísérleti meghatározásának egyik lehetséges módszere a csillapodási hányados mérésén alapul. Ekkor egymás utáni lengések amplitúdócsökkenéseit mérjük. Ennek észlelése akkor pontos, ha a lengő rendszer periódusideje eléggé nagy (kb. 3-10 s). Az alkalmazott rugónál a lengésidő rövidebb, emiatt egy másik módszer alkalmazása előnyösebb: a csillapítási- és jósági tényezők a sebességamplitúdó frekvenciafüggéséből meghatározhatók.

Illesszen a 3. pontban mért sebességamplitúdó adatokra a sebességamplitúdó – körfrekvencia függvénynek megfelelő görbét! 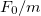Az illesztett görbe illesztési paraméterei között szerepel a $\setbox0\hbox{$\beta$}% \message{//depth:\the\dp0//}% \box0%$ csillapítási tényező és az $\setbox0\hbox{$\omega_0$}% \message{//depth:\the\dp0//}% \box0%$ saját körfrekvencia (valamint az $\setbox0\hbox{$F_0/m$}% \message{//depth:\the\dp0//}% \box0%$ hányados). Az illesztés alapján határozza meg ezeket a paramétereket és hibájukat. Ezek alapján már meghatározható a jósági tényező is.

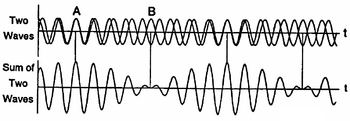
5. Lebegés vizsgálata

5. ábra

Két, kis mértékben különböző frekvenciájú, szinuszhullám szuperpozíciójakor „lebegés” alakul ki (5. ábra). Ha 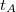$\setbox0\hbox{$t_A$}% \message{//depth:\the\dp0//}% \box0%$ időpontban a rezgések éppen fázisban vannak, akkor a hullámok összeadódnak és az eredő rezgés maximális amplitúdójú lesz. Egy későbbi 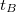$\setbox0\hbox{$t_B$}% \message{//depth:\the\dp0//}% \box0%$ időpontban azonban a frekvencia különbség miatt a rezgések ellentétes fázisba kerülnek, és egymás hatását csökkentve minimális amplitúdót eredményeznek. Az amplitúdó változások burkológörbéje szintén szinuszos. 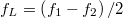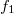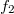A burkológörbe frekvenciája $\setbox0\hbox{$f_L=\left(f_1-f_2\right)/2$}% \message{//depth:\the\dp0//}% \box0%$, ahol $\setbox0\hbox{$f_1$}% \message{//depth:\the\dp0//}% \box0%$ és $\setbox0\hbox{$f_2$}% \message{//depth:\the\dp0//}% \box0%$ a két összetevő rezgés frekvenciája.

A kényszerrezgés bekapcsolásakor az állandósult tag mellett egy darabig megfigyelhető a csillapított rendszer idővel elhaló saját rezgése is. A differenciálegyenlet megoldása tartalmazza a bekapcsolás után kialakuló mindkét frekvenciát. A tranziens rezgés körfrekvenciája 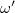$\setbox0\hbox{$\omega’$}% \message{//depth:\the\dp0//}% \box0%$, az állandósulté pedig $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$. 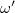Lebegés akkor figyelhető meg, ha a kényszererő $\setbox0\hbox{$\omega$}% \message{//depth:\the\dp0//}% \box0%$ körfrekvenciája $\setbox0\hbox{$\omega’$}% \message{//depth:\the\dp0//}% \box0%$ közelében van, és a csillapítás elég kicsi. Amint a tranziens elhal, a lebegés is megszűnik.

Szerelje le újra a csillapító mágnespofákat és állítsa be pontosan a mérőrúd helyzetét. Határozza meg a rendszer sajátfrekvenciáját! (A 2. méréshez hasonlóan használja a készülék kijelzőjén a PERIOD állást! 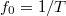$\setbox0\hbox{$f_0=1/T$}% \message{//depth:\the\dp0//}% \box0%$) Állítsa a kényszerkeréken az amplitúdót 2 mm-re! Kapcsolja be a kényszermozgást és szabályozza annak frekvenciáját úgy, hogy 0,1 Hz-cel legyen alacsonyabb, mint $\setbox0\hbox{$f_0$}% \message{//depth:\the\dp0//}% \box0%$! Jegyezze fel mindét frekvencia értékét és kapcsolja ki a kényszert! Várjon, amíg a mérőrúd megáll! Állítsa a funkciókapcsolót AMPL. állásba.

Helyezze a mérőrúd alá az ultrahangos érzékelőt! Indítsa el a számítógépen a Logger Lite programot. A program felismeri a rákapcsolt szenzort. Végezze el a következő beállításokat: Experiment $\setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0%$ Data Collection $\setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0%$ Length: 120 s; Options $\setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0%$ Graph Options $\setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0%$ Axes Options $\setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0%$ Scaling: Autoscale (mindkét tengelyen).

Indítsa el az adatgyűjtést, majd kapcsolja be a kényszerrezgést! A lebegés megszűntéig mérjen! Utána a mérési adatok a File $\setbox0\hbox{$\to$}% \message{//depth:\the\dp0//}% \box0%$ Export as paranccsal menthetők.

Ábrázolja az amplitúdót az idő függvényében! Határozza meg a burkoló szinuszgörbe periódusidejét és frekvenciáját!

• Vesse össze az elmélet alapján várható értékekkel!
• Akkor kap szép lebegést, ha kicsi a csillapítás (leszedett mágnespofák, jól beállított mérőrúd (nem súrlódik).

FONTOS! Ebből a mérésból és az RLC körök méréséből közös jegyzőkönyvet kell készítenie a második mérést követő héten. A jegyzőkönyvben térjen ki a két mérés közös vonásaira, mutasson rá az egymásnak megfelelő, egymással analóg jelenségekre - és a méréstechnikai vagy más különbségekre is!

Vissza a Fizika laboratórium 1. tárgyoldalára.