Magneto-optikai Kerr-szög mérése
Tartalomjegyzék[elrejtés] |
Szerkesztés alatt!
Elméleti összefoglaló
Bevezetés
A számítástechnika fejlődése napjainkban egyre nagyobb kapacitású adattároló eszközöket igényel. A nagytömegű adattárolás egyik jellemző eszközcsaládja az optikai adattárolók. Bennük az információ kiolvasása optikai úton, fény segítségével történik. Az információs egység legkisebb méretét ily módon a fény hullámhossza és az optikai leképező rendszer minősége (elsősorban az alkalmazott fókuszáló lencse numerikus apertúrája) határozza meg.
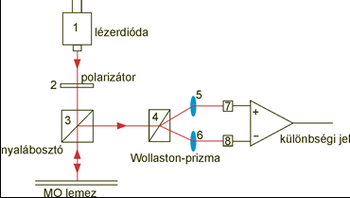
Az optikai adattárolás napjainkban elterjedt eszközei a compact disc (CD), és a digital versatile disc (DVD), melyek újraírható, törölhető optikai lemezt használnak, egyesítve a winchester típusú merev mágneslemezes eszközök nagy kapacitását a floppy lemezek cserélhetőségével. A fentiekhez hasonló tárolókapacitással és hozzáférési sebességekkel jellemezhető rendszer a magneto-optikai (MO) tároló (a cserélhető, CD-méretű MO lemezek kapacitása kb. 5,2 Gbyte), melyben az információ tárolása mágneses úton, kiolvasása pedig optikailag történik. MO adathordozókkal és meghajtókkal Európában kevésbé találkozhatunk, alkalmazásuk a távol-keleten, elsősorban Japánban elterjedt. A MO lemez kiolvasása a magneto-optikai Kerr-effektus segítségével történik.
Elméleti alapok
A mérés során vizsgált jelenség, a magneto-optikai Kerr-effektus (MOKE), a fény polarizációs természetével van kapcsolatban, ezért most röviden összefoglaljuk az ide tartozó optikai alapismereteket. A fény transzverzális elektromágneses hullám, melyben az energiaterjedés iránya (Poynting-vektor), az elektromos térerősség vektor (E) és a mágneses térerősség vektor (H) kölcsönösen merőlegesek egymásra. Természetes (polarizálatlan) fényben nincs kitüntetett rezgési irány, az ilyen sugárzás végtelen sok, független, különböző irányú E vektorral jellemezhető rezgés összegeként írható le. Polarizált fényben az elektromos térerősség vektor végpontja szabályos görbét ír le a fényterjedés iránya körül. E görbének a terjedés irányára merőleges síkra vett vetülete általános esetben ellipszis, amely speciális esetben egyenessé (lineárisan polarizált fény), vagy körré (cirkulárisan polarizált fény) fajulhat. Mivel minden elektromágneses hullám felbontható kölönböző frekvenciájú és irányú síkhullámok összegére (ld. szögspektrumra bontás vagy 2D Fourier-transzformáció), az egyszerűség kedvéért most csak egy, a z-irányba terjedő, ω körfekvenciájú monokromatikus síkhullámot, E(z, t)-t vizsgálunk. A komplex formalizmus alkalmazásával a terjedési irányra merőleges x-y síkban a térerősség vektorkomponensei a következő alakban írhatók fel:
![\[\mathbf{E_x}\left (z,t \right ) {{=}} \mathbf{E}_{x0} \cdot e^{i(\omega t - kz + \phi_x)}\]](/images/math/a/5/6/a56d307a1136200340ac56387da645cf.png)
![\[\mathbf{E_y}\left (z,t \right ) = \mathbf{E}_{y0} \cdot e^{i(\omega t - kz + \phi_{y})}\]](/images/math/f/8/0/f802582c388baaf9692ecabfaa64c3c5.png)
ahol „k” a hullámszám vektor abszolút értéke, 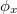 és
és 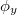 az x és y irányú vektorkomponensek kezdőfázisai,
az x és y irányú vektorkomponensek kezdőfázisai, 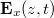 és
és 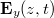 komplex,
komplex, 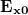 és
és 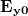 pedig valós vektorok. (Emlékeztetőül: a valódi térerősségvektor komponensek értékét a komplex vektorkomponensek valós részei képezik.) Általános esetben tehát
pedig valós vektorok. (Emlékeztetőül: a valódi térerősségvektor komponensek értékét a komplex vektorkomponensek valós részei képezik.) Általános esetben tehát 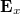 és
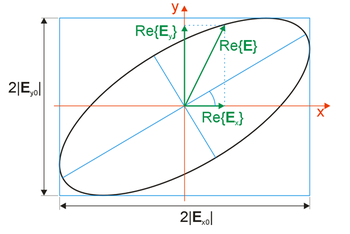
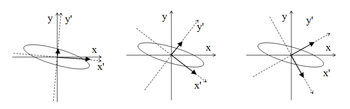
és 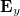 valós eredője ellipszist ír le (1. ábra), melyet a kis- és nagytengelyek hossza, a nagytengely és az x tengely által bezárt szög és térerősségvektor forgási iránya jellemez. Speciálisan, ha
valós eredője ellipszist ír le (1. ábra), melyet a kis- és nagytengelyek hossza, a nagytengely és az x tengely által bezárt szög és térerősségvektor forgási iránya jellemez. Speciálisan, ha 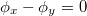 vagy 180°, az E mindig egy egyenesbe esik, így a fény lineárisan poláros. Ha az x és y komponensek
vagy 180°, az E mindig egy egyenesbe esik, így a fény lineárisan poláros. Ha az x és y komponensek 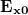 ,
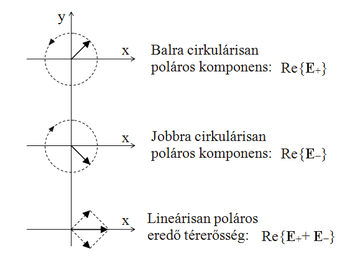
, 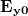 amplitúdóinak abszolút értékei megegyeznek, és közöttük 90° vagy 270° a fáziskülönbség, az elektromos térerősségvektor végpontja egy kör mentén fog az első esetben jobbra, a második esetben balra forogni. A fény ekkor jobbra vagy balra cirkulárisan poláros.
amplitúdóinak abszolút értékei megegyeznek, és közöttük 90° vagy 270° a fáziskülönbség, az elektromos térerősségvektor végpontja egy kör mentén fog az első esetben jobbra, a második esetben balra forogni. A fény ekkor jobbra vagy balra cirkulárisan poláros.
Mivel vizsgálatainkat monokromatikus sugárzásra korlátozzuk, a térerősségek időfüggését (azaz az ωt-s tagot) a továbbiakban elhagyjuk. Ráadásul az elektromágneses teret csak egyetlen síkhullámra, a tér egyetlen pontjában akarjuk meghatározni, így a helyfüggés (k∙z) is elhagyható, azaz elegendő számításainkat csupán a térerősség komplex amplitudóin végezni:
![\[\mathbf{E_x} {{=}} \mathbf{E}_{x0} \cdot e^{i\phi_x}\]](/images/math/4/2/d/42df04c2f57faac12be2d8f7009f822a.png)
\[\mathbf{E_y} = \mathbf{E}_{y0} \cdot e^{i\phi_{y\]
Optikai aktivitás
A magneto-optikai Kerr-effektus (MOKE) egyes anyagok speciális anizotrópiájának a következménye: olyan közegekben lép fel, amelyek ún. optikai aktivitást mutatnak. A MOKE megértéséhez tehát meg kell ismerkednünk az optikai aktivitás jelenségével. Léteznek olyan anyagok, amelyeken ha lineárisan polarizált síkhullám halad át, a kilépő fény polarizációs síkja az anyagvastagságtól függő mértékben elfordul – az ilyen effektust kiváltó anyagokat nevezik optikailag aktív közegeknek. Mivel ez a jelenség általános formában csak igen bonyolult módon írható le, jelen mérési leírásban megelégszünk az optikai aktivitás jelentősen leegyszerűsített tárgyalásával.
Az anizotrópia tejredési irány és polarizáció függő fényterjedést jelent. Anizotróp közegekben az E elektromos térerősség vektor és a D dielektromos eltolás vektor közötti kapcsolat a következő egyenletrendszerrel írható le:
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
ahol ε az ún. dielektromos tenzor, melynek elemei általános esetben komplex értékűek. A legtöbb közegben található egy olyan x-y-z koordináta rendszer (ld. kristálytani tengelyek), ahol ε diagonálisra redukálódik. Általános esetben azonban a dielektromos tenzor nem diagonális és nem is konstans, elemei függnek az elektromos/mágneses térerősségektől és ezek deriváltjaitól. Ezen anyagok tárgyalásával a nemlineáris optika foglalkozik. A nem-lineáris közegek egy csoportjában az elektromos térerősség hely szerinti deriváltjától függő komponenseket is tartalmaz ε, amelyről belátható, hogy síkhullám terjedés, valamint egytengelyű anizotrópia esetén a következő alakú lesz (a tenzorelemek általános esetben komplex értékűek!):
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
Ezek az ún. optikai aktivitást mutató anyagok. A fenti képletből következik, hogy ilyen közegekben a z-irány kitüntetett szereppel bír: ez az anyag szimmetria tengelye (optikai tengelynek is nevezik). Ilyenek egyes kristályok pl. a kvarc (SiO2) vagy a tellúrdioxid (TeO2). (Optikailag lehetnek aktívak izotróp közegek is, pl. higanyszulfid (HgS) vagy a közönséges cukoroldat; ekkor εxx = εzz.) A továbbiakban feltételezzük, hogy az optikai tengely egybeesik a fény terjedési irányával, azaz a z-tengellyel, tehát (4)-et behelyettesítve (3)-ból a következő másodrendű egyenletrendszer marad:
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
Az ilyen anyagokban (z-irányú fényterjedés esetén) létezik két olyan E+ és E− vektor, amelyekből a hozzájuk tartozó D± vektorok skalárral való szorzással kaphatók meg:
![\[\]](/images/math/d/2/f/d2f200551b1010b2a734d78b13930a09.png)
Mérési feladatok
PDF formátum
Magneto-optikai Kerr-szög mérése