Hall-effektus
Szerkesztés alatt!
A mérés célja:
- a félvezetők néhány fontos vezetési tulajdonságának, és a mágneses tér által okozott néhány effektusnak a megismertetése.
A cél érdekében:
- összefoglaljuk a vezetésre és a mágneses effektusokra vonatkozó legfontosabb elméleti ismereteket,
- ismertetjük az elektromos vezetőképesség, a tiltott sáv-szélesség, a mágneses ellenállás és a Hall-effektus mérésének módszerét,
- vezetőképesség- és Hall-effektus méréseket végzünk szennyezett germánium (Ge) mintán.
Tartalomjegyzék |
Elméleti összefoglaló
Elektronvezetés félvezetőkben
Az anyagokban külső elektromos tér ( ) hatására létrejött elektromos áram felületi áramsűrűségét (
) hatására létrejött elektromos áram felületi áramsűrűségét ( ) az ismert
) az ismert
![\[ j_k = \gamma_{kl} E_l \]](/images/math/e/c/0/ec01c40f13174b6c6dfb4ad9830827f6.png)
összefüggés adja meg, ahol az indexek a koordinátatengelyekre utalnak, 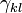 a fajlagos vezetőképesség tenzora. Az egyenletben az Einstein-féle összegzési konvenciót alkalmaztuk, tehát az
a fajlagos vezetőképesség tenzora. Az egyenletben az Einstein-féle összegzési konvenciót alkalmaztuk, tehát az  indexre összegezni kell. (A jelenségek tenzoros leírásáról részletesebben
indexre összegezni kell. (A jelenségek tenzoros leírásáról részletesebben  . a "Piezoelektromos állandók mérése" c. segédletet.) Izotróp- vagy elektromos vezetés szempontjából annak tekinthető anyagokban (ilyen például az általunk vizsgált germánium is) a vezetőképességet egyetlen állandóval jellemezhetjük, és így a fenti egyenlet az egyszerűbb
. a "Piezoelektromos állandók mérése" c. segédletet.) Izotróp- vagy elektromos vezetés szempontjából annak tekinthető anyagokban (ilyen például az általunk vizsgált germánium is) a vezetőképességet egyetlen állandóval jellemezhetjük, és így a fenti egyenlet az egyszerűbb
\[ \v{j} = \gamma \v{E} \]
alakba írható. Az áramsűrűség kifejezhető molekuláris adatokkal is:
\[ \v{j} = q n \v{v} \]
ahol  a töltéshordozók koncentrációja,
a töltéshordozók koncentrációja,  azok töltése és
azok töltése és  a töltéshordozók átlagos sebessége, amely arányos a térerősséggel
a töltéshordozók átlagos sebessége, amely arányos a térerősséggel
\[ \v{v} = \mu '''E''' \]
ahol  a töltéshordozók mozgékonysága.
A (1), (2), (3) és (4) összefüggésekből a vezetőképesség az alábbi módon fejezhető ki:
a töltéshordozók mozgékonysága.
A (1), (2), (3) és (4) összefüggésekből a vezetőképesség az alábbi módon fejezhető ki:
![\[ \gamma = q n \mu \]](/images/math/2/e/f/2efbde9fca7bf586551523631c99feb9.png)
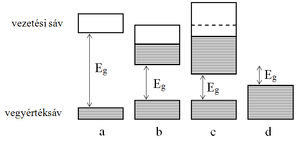
Mivel itt csak elektronvezetéssel foglalkozunk, a töltéshordozók töltése adott, így a vezetési tulajdonságokat alapvetően a töltéshordozók koncentrációja és azok mozgékonysága szabja meg. Méréseink során egyik feladatként félvezetők vezetőképességének hőmérsékletfüggését vizsgáljuk, amit döntően a töltéshordozók koncentrációjának hőmérsékletfüggése okoz. Ezért részletesebben csak a töltéshordozók létrejöttének magyarázatával foglalkozunk. (Megjegyezzük, hogy fémekben fordított a helyzet: ott többnyire a töltéshordozó-koncentráció hőmérsékletfüggése hanyagolható el, így a mozgékonyság hőmérsékletfüggése igen fontos szerepet játszik.) Tapasztalatból tudjuk, hogy a különböző anyagok elektromos vezetési tulajdonságai igen eltérőek lehetnek: szobahőmérsékleten a legjobb vezetők és a legjobb szigetelők fajlagos ellenállása (vezetőképessége) között durván 25 nagyságrend eltérés van. A jó vezetőkben az elektromos áram elektronok mozgásából származik, míg a legjobb szigetelőkben az elektronáram olyan kicsi, hogy a – csak nagyon kis áramok létrehozására képes – ionmozgások is nagyobb áramot hoznak létre. Azt a tényt, hogy az anyagok elektronmozgásból származó vezetőképessége ilyen széles skálán mozog, a szilárd anyagok sávelméletének segítségével sikerült értelmezni, amelynek legfontosabb eredményeit az alábbiakban vázlatosan összefoglaljuk. A szabályos atomelrendeződésű szilárd anyagokban (a kristályokban) – a különálló atomoktól eltérően – az elektronok nem diszkrét energiaértékekkel rendelkezhetnek, hanem energiájuk bizonyos energiasávokba, az ún. megengedett sávokba, eshet. A sávokban – az atomi energiaszintekhez hasonlóan – meghatározott számú elektron foglalhat helyet, és a sávon belül az elektron energiája gyakorlatilag folytonosan változhat, az elektron tehát mozoghat a betöltetlen állapotok között. Az energiasávok betöltöttségét a legtöbb esetben az határozza meg, hogy milyen a kristályt alkotó atomokban az energiaszintek betöltöttsége. Ha a kristályt alkotó egyedülálló atomban egy energiaszint betöltött, akkor a megfelelő energiasáv a kristályban is betöltött lesz, részben betöltött atomi energiaszintnek pedig részben betöltött energiasáv felel meg. Az energiasávok betöltöttségének a kristály tulajdonságai szempontjából igen nagy jelentősége van: a kristály egy energiasávjában helyet foglaló elektront ugyanis külső elektromos térrel csak akkor lehet könnyen mozgatni, ha energiája könnyen változtatható, azaz a sávon belül vannak üres energiaállapotok. A jó elektromos vezetés alapfeltétele tehát az, hogy a kristályban legyen részben betöltött energiasáv. Az ilyen sávot ennek megfelelően vezetési sávnak nevezik. A kristályok elektronsáv-szerkezetének három alaptípusa van, ezeket az 1. ábrán mutatjuk be.
Ha az elektronokat tartalmazó legmagasabb energiasáv betöltött (1.a ábrán), akkor itt az elektronok külső térrel nem mozgathatók, az elektromos vezetésben nem vesznek részt. Az ilyen betöltött sávot vegyértéksávnak nevezik. Ebben az esetben elektronvezetés csak úgy képzelhető el, hogy energiaközléssel folyamatosan elektronokat juttatunk a magasabb – eredetileg üres – sávba, ahol azok már mozgásképesek lesznek (ilyenkor ez a sáv is részben betöltötté válik, ezért a legfelső betöltött sáv feletti üres sávot is vezetési sávnak nevezik). A folyamatos energiaközlés azért szükséges, mert a vezetési sávba feljuttatott elektronok spontán visszatérnek a vegyértéksávba. Ha nincs olyan külső hatás, amely kellő számú elektront juttatna a vezetési sávba (a szokásosan alkalmazott elektromos terek erre rendszerint nem képesek), akkor az anyagban kis elektromos térrel számottevő elektronáram nem hozható létre. Az ilyen sávszerkezettel rendelkező anyagok a szigetelők. A sávszerkezet másik lehetséges típusa az, amelynél az elektronokat tartalmazó legfelső energiasáv csak részben van betöltve (1.b ábra), így már kis elektromos térrel is jelentős elektronmozgás hozható létre. Az ilyen típusú sávszerkezettel rendelkező anyagok a vezetők. Előfordul, hogy olyan anyagok is jó vezetők, amelyeknek legfelső energiasávja betöltött, tehát tulajdonképpen szigetelőknek kellene lenniük. Ez annak a következménye, hogy a betöltött legfelső energiasáv átfedésbe kerül a felette lévő üres sávval (1.c ábra), ami végeredményben vezető típusú sávszerkezetet eredményez.
Mivel a természetben van egy mindig jelenlévő energiaközlő hatás, a termikus mozgás, a szigetelő típusú anyagokban is létrejöhet elektronvezetés, hiszen a termikus energia révén elektronok juthatnak a vezetési sávba, ahol már külső térrel meghatározott irányú mozgásba hozhatók. Ebből következik, hogy ezeknek az anyagoknak az elektromos tulajdonságait lényegesen befolyásolja a vegyértéksáv és a vezetési sáv között elhelyezkedő energiatartomány, az ún. tilos sáv szélessége (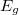 ), és az anyag hőmérséklete (
), és az anyag hőmérséklete ( ). Ha az atomok átlagos termikus energiája (nagyságrendben
). Ha az atomok átlagos termikus energiája (nagyságrendben 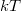 ) összemérhető a tilos sáv szélességével, akkor a vezetési sávban jelentős számú mozgásképes elektron jelenhet meg, és így az anyag elektromos vezetőképessége sok nagyságrenddel nagyobb lehet, mint a legjobb szigetelőké. Ezzel magyarázható az, hogy nem csak jó vezetők és jó szigetelők léteznek, hanem olyan anyagok is, amelyeknek szobahőmérsékleten mért vezetőképessége a 25 nagyságrendet átfogó tartomány közepe táján helyezkedik el. Ezeket az anyagokat félvezetőknek nevezik (szigetelő kis
) összemérhető a tilos sáv szélességével, akkor a vezetési sávban jelentős számú mozgásképes elektron jelenhet meg, és így az anyag elektromos vezetőképessége sok nagyságrenddel nagyobb lehet, mint a legjobb szigetelőké. Ezzel magyarázható az, hogy nem csak jó vezetők és jó szigetelők léteznek, hanem olyan anyagok is, amelyeknek szobahőmérsékleten mért vezetőképessége a 25 nagyságrendet átfogó tartomány közepe táján helyezkedik el. Ezeket az anyagokat félvezetőknek nevezik (szigetelő kis 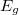 -vel; 1.d ábra.
-vel; 1.d ábra.
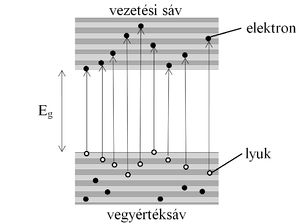
Könnyen belátható, hogy a termikus gerjesztés fenti folyamata kettős hatás révén növeli a mozgásképes töltéshordozók számát. Egyrészt elektronokat juttat a vezetési sávba, másrészt a vegyértéksávban üres elektronhelyeket hoz létre (2. ábra), így ott is lehetségessé válik az elektronok energiaváltozása, és ezzel az elektromos töltéstranszportban való részvételük is. A vegyértéksáv elektronjai által létrehozott elektromos áram formálisan egyszerűbben leírható, ha azt nem az elektronoknak a térrel ellentétes irányú mozgásaként, hanem a pozitív töltésű elektronhiányoknak, az ún. lyukaknak a tér irányában történő mozgásaként fogjuk fel. Az elektronoknak a vegyértéksávból a vezetési sávba történő közvetlen gerjesztésével – tehát azonos számú elektronnal és lyukkal (elektron-lyuk párokkal) – létrejött vezetés a tiszta félvezetők jellegzetes vezetési mechanizmusa, amelyet sajátvezetésnek neveznek.
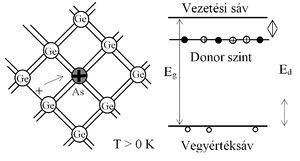
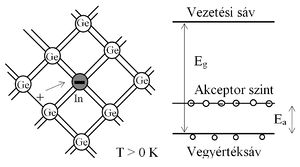
Bizonyos szennyező atomok jelenléte egy félvezető anyagban újabb töltéshordozók, és egy új vezetési mechanizmus, az ún. szennyezéses vezetés, megjelenését eredményezi. A szennyezéses vezetés egyik típusát az alaprács atomjainál nagyobb vegyértékű szennyező atomok (Ge-ban pl. As) hozzák létre, amelyeknek "felesleges" elektronjai könnyen elválaszthatók az atomjaiktól, és a rácsban mozogni képesek. Az energiasáv-sémában ez úgy jelentkezik (3.a ábra), hogy ezek az elektronok a vezetési sáv alatt, annak közelében lévő energia-szinteken helyezkednek el, és a tilos sáv szélességénél jóval kisebb energiával (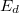 ) a vezetési sávba juttathatók. A többletelektront adó szennyezőt donor szennyezőnek, a létrehozott új energiaszintet donor szintnek nevezik. A szennyezéses vezetés egy másik típusát az alaprács atomjainál kisebb vegyértékű (Ge-ban pl. In) szennyező atomok okozzák. Ezeknek az atomoknak elektron-hiánya van, ezért hajlamosak elektront megkötni. A vegyérték-sávból viszonylag kis energia hatására elektronok juthatnak át ezekbe az atomokba, miáltal a vegyértéksávban lyukak jönnek létre. Az energiasáv-sémában ez úgy értelmezhető, hogy ezek az atomok a vegyértéksáv felett, ahhoz közel üres energiaszinteket hoznak létre, amelyekre a vegyértéksávból kis energiával (
) a vezetési sávba juttathatók. A többletelektront adó szennyezőt donor szennyezőnek, a létrehozott új energiaszintet donor szintnek nevezik. A szennyezéses vezetés egy másik típusát az alaprács atomjainál kisebb vegyértékű (Ge-ban pl. In) szennyező atomok okozzák. Ezeknek az atomoknak elektron-hiánya van, ezért hajlamosak elektront megkötni. A vegyérték-sávból viszonylag kis energia hatására elektronok juthatnak át ezekbe az atomokba, miáltal a vegyértéksávban lyukak jönnek létre. Az energiasáv-sémában ez úgy értelmezhető, hogy ezek az atomok a vegyértéksáv felett, ahhoz közel üres energiaszinteket hoznak létre, amelyekre a vegyértéksávból kis energiával (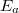 ) elektronok juttathatók fel (3.b ábra). Az ilyen elektronmegkötő szennyező neve akceptor szennyező, a létrehozott energiaszintek az akceptorszintek.
) elektronok juttathatók fel (3.b ábra). Az ilyen elektronmegkötő szennyező neve akceptor szennyező, a létrehozott energiaszintek az akceptorszintek.
Mivel 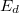 és
és 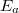 általában sokkal kisebb, mint E_g, a szennyezéses vezetés alacsony hőmérsékleten játszik jelentős szerepet, ahol a sajátvezetést okozó elektron-lyuk párok gerjesztéséhez a termikus energia már nem elegendő. Ilyenkor a donor szennyezőt tartalmazó anyagban gyakorlatilag elektronvezetés, az akceptor szennyezést tartalmazó anyagban pedig lyukvezetés van. Az első esetben, amikor a többségi töltéshordozók elektronok, a félvezetőt gyakran n-típusú félvezetőnek, a másodikban pedig, amikor a többségi töltéshordozók lyukak, p-típusú félvezetőnek nevezik.
Szennyezett félvezetőben egyidejűleg többféle töltéshordozó van jelen: a sajátvezetési mechanizmus útján keletkezett, azonos koncentrációjú vezetési elektron és lyuk, valamint a szennyezések által létrehozott töltéshordozók (elektronok vagy lyukak). Kimutatható, hogy az elektron-lyuk párok
általában sokkal kisebb, mint E_g, a szennyezéses vezetés alacsony hőmérsékleten játszik jelentős szerepet, ahol a sajátvezetést okozó elektron-lyuk párok gerjesztéséhez a termikus energia már nem elegendő. Ilyenkor a donor szennyezőt tartalmazó anyagban gyakorlatilag elektronvezetés, az akceptor szennyezést tartalmazó anyagban pedig lyukvezetés van. Az első esetben, amikor a többségi töltéshordozók elektronok, a félvezetőt gyakran n-típusú félvezetőnek, a másodikban pedig, amikor a többségi töltéshordozók lyukak, p-típusú félvezetőnek nevezik.
Szennyezett félvezetőben egyidejűleg többféle töltéshordozó van jelen: a sajátvezetési mechanizmus útján keletkezett, azonos koncentrációjú vezetési elektron és lyuk, valamint a szennyezések által létrehozott töltéshordozók (elektronok vagy lyukak). Kimutatható, hogy az elektron-lyuk párok 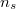 koncentrációja
koncentrációja
\[ n_s = A_s e^{\frac{-E_g}{2kT\]
ahol 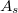 az anyagi minőségtől és a hőmérséklettől (az exponenciálisnál gyengébben) függő faktor. Hasonló kifejezés érvényes a szennyezés által okozott töltéshordozók koncentrációjára alacsony hőmérsékleten
az anyagi minőségtől és a hőmérséklettől (az exponenciálisnál gyengébben) függő faktor. Hasonló kifejezés érvényes a szennyezés által okozott töltéshordozók koncentrációjára alacsony hőmérsékleten 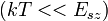 :
:
![\[ n_{sz} = A_{sz} e^{\frac{-E_{sz} }{kT} } \]](/images/math/b/5/8/b58642931aa7f5a00f77d300b7b41e9c.png)
ahol az 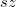 index
index  -t vagy
-t vagy  -t jelent, attól függően, hogy donor- vagy akceptor szennyezőről van szó,
-t jelent, attól függően, hogy donor- vagy akceptor szennyezőről van szó, 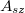 pedig az anyagi minőségtől, a töltéshordozó típusától és a hőmérséklettől (az exponenciálisnál gyengébben) függő faktor. Magas hőmérsékleten
pedig az anyagi minőségtől, a töltéshordozó típusától és a hőmérséklettől (az exponenciálisnál gyengébben) függő faktor. Magas hőmérsékleten 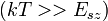
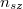 a hőmérséklettől gyakorlatilag független, és közelítőleg egyenlő a szennyező atomok koncentrációjával.
Többféle (de azonos töltésű) töltéshordozót tartalmazó anyag vezetőképessége (
a hőmérséklettől gyakorlatilag független, és közelítőleg egyenlő a szennyező atomok koncentrációjával.
Többféle (de azonos töltésű) töltéshordozót tartalmazó anyag vezetőképessége ( ) a töltéshordozó töltésével (
) a töltéshordozó töltésével ( ), a töltéshordozó-koncentrációkkal (
), a töltéshordozó-koncentrációkkal (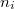 ) és a töltéshordozók mozgékonyságaival (
) és a töltéshordozók mozgékonyságaival (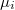 ) az alábbi módon fejezhető ki:
) az alábbi módon fejezhető ki:
![\[ \gamma = q \sum_{i} n_i \mu_i\]](/images/math/4/4/4/44433af9c53dd7bfc465835412ce95b6.png)
A mérés során a vezetőképesség hőmérsékletfüggésének azt a tartományát vizsgáljuk, ahol a sajátvezetés dominál, vagyis 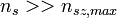 (ha a szennyezés vegyértéke eggyel tér el az alaprácsétól, akkor a szennyezés által keltett töltéshordozók koncentrációja maximum a szennyezés-koncentrációval lehet egyenlő). Ebben a tartományban a vezetőképesség
(ha a szennyezés vegyértéke eggyel tér el az alaprácsétól, akkor a szennyezés által keltett töltéshordozók koncentrációja maximum a szennyezés-koncentrációval lehet egyenlő). Ebben a tartományban a vezetőképesség
![\[ \gamma_s = q n_s \left( \mu_{el}+\mu_{lyuk}\right)\]](/images/math/6/f/9/6f9ef400cd2e810980f385645ef8135c.png)
ami (6) felhasználásával és a 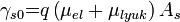 jelölés bevezetésével az alábbi alakba írható
jelölés bevezetésével az alábbi alakba írható
![\[ \gamma_{s} = \gamma_{s0} e^{\frac{-E_g}{2kT} } \]](/images/math/a/7/3/a735ebd1a9d25e732e8612bc4096621a.png)
Itt 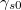 hőmérséklet-független állandó (a mozgékonyság és az
hőmérséklet-független állandó (a mozgékonyság és az 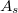 faktor hőmérsékletfüggése éppen kiejti egymást). A (10) egyenlet segítségével a tilos sáv szélessége meghatározható: a minta különböző hőmérsékleteken mért ellenállásából a vezetőképességet kiszámítva, majd elkészítve az
faktor hőmérsékletfüggése éppen kiejti egymást). A (10) egyenlet segítségével a tilos sáv szélessége meghatározható: a minta különböző hőmérsékleteken mért ellenállásából a vezetőképességet kiszámítva, majd elkészítve az 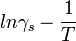 grafikont, a pontokhoz egyenes illeszthető, amelynek
grafikont, a pontokhoz egyenes illeszthető, amelynek  meredeksége éppen
meredeksége éppen 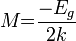 , amiből
, amiből
![\[ E_g = -2 k M \]](/images/math/0/4/2/042f96722f412e4749c792c00eef428f.png)
A vezetőképesség nem csak a hőmérséklettől függ, hanem minden olyan hatás befolyásolja, amely a töltéshordozók koncentrációját vagy azok mozgékonyságát módosítja. Előbbire példa a fotóvezetés, ahol a töltéshordozó-koncentráció fotonok hatására módosul, utóbbira példa a mágneses ellenállás, amelyet a mérés során is megvizsgálunk. Kimutatható, hogy a töltéshordozók mozgékonysága arányos a töltéshordozók szabad úthosszával, a szabad úthossz pedig lecsökken, ha az anyagot mágneses térbe tesszük. A vezetőképesség csökkenése ellenállás-növekedést jelent, vagyis a mágneses tér ellenállástöbbletet – ún. mágneses ellenállást – okoz. Ennek jellemzésére a relatív ellenállás-változást, vagyis az
![\[\frac{R_m-R_0}{R_0}\]](/images/math/6/8/f/68f87573fe2e48b4573896acb7c2c54c.png)
hányadost használják (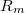 a térben,
a térben, 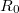 a tér nélkül mért ellenállás).
a tér nélkül mért ellenállás).
A Hall-effektus
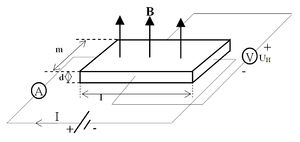
Ha egy derékszögű hasáb alakú félvezető lapka (4.ábra) egyik hosszú élével párhuzamosan áram ( ) folyik, és a lapkára merőleges irányban mágneses teret (
) folyik, és a lapkára merőleges irányban mágneses teret ( ) hozunk létre, akkor a mágneses térre és az áramra merőleges irányban a mintán elektromos feszültség (
) hozunk létre, akkor a mágneses térre és az áramra merőleges irányban a mintán elektromos feszültség ( ) jön létre. A jelenséget Hall-effektusnak, a létrejött
) jön létre. A jelenséget Hall-effektusnak, a létrejött  feszültséget Hall-feszültségnek nevezik.
A jelenséget a mágneses térben mozgó töltéshordozókra ható Lorentz-erő okozza, amely a
feszültséget Hall-feszültségnek nevezik.
A jelenséget a mágneses térben mozgó töltéshordozókra ható Lorentz-erő okozza, amely a 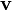 sebességgel mozgó töltéshordozók eltérítésével
sebességgel mozgó töltéshordozók eltérítésével
\[ \v{E_H} = -\v{v} \times \v{B} \]
elektromos teret hoz létre (vö. mozgási indukció). A 4.ábra elrendezése esetén a térerősség nagysága tehát
![\[E_H = v B\]](/images/math/1/9/3/193433294c6e366cf4c38e66fafafcda.png)
Feltételezve, hogy a vezetést egyfajta,  koncentrációban jelenlévő töltéshordozó hozza létre (félvezetőben ez a szennyezéses vezetés tartományában áll fenn), a (3) és (14) egyenletekből a Hall-térerősségre az alábbi kifejezést kapjuk:
koncentrációban jelenlévő töltéshordozó hozza létre (félvezetőben ez a szennyezéses vezetés tartományában áll fenn), a (3) és (14) egyenletekből a Hall-térerősségre az alábbi kifejezést kapjuk:
![\[ E_H = \frac{jB}{qn}= R_H j B\]](/images/math/9/b/8/9b80710543fac62e3b311e9b9e5bbaa7.png)
Itt bevezettük az
![\[ R_H = \frac{1}{q n}\]](/images/math/b/d/c/bdcbcd94908c72a193d676cbab658625.png)
ún. Hall-állandót ( a töltéshordozó-koncentráció).
Az áramsűrűséget kifejezve a mintán átfolyó
a töltéshordozó-koncentráció).
Az áramsűrűséget kifejezve a mintán átfolyó  árammal, a
árammal, a  él mentén fellépő Hall-térerősséget pedig homogénnek feltételezve, a Hall-feszültségre azt kapjuk, hogy
él mentén fellépő Hall-térerősséget pedig homogénnek feltételezve, a Hall-feszültségre azt kapjuk, hogy
![\[ U_H = R_H \frac{I B}{d}\]](/images/math/c/8/e/c8e29ea91fa974e5135ae817dcc72c68.png)
A Hall-feszültség tehát mind a mintán átfolyó árammal, mind pedig a mágneses indukcióval arányos. Emiatt, ha például adott  és
és  értékek mellett mérjük, és grafikonon ábrázoljuk a Hall-feszültségnek a mágneses indukciótól való függését, akkor a mérési pontokhoz illesztett egyenes
értékek mellett mérjük, és grafikonon ábrázoljuk a Hall-feszültségnek a mágneses indukciótól való függését, akkor a mérési pontokhoz illesztett egyenes 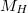 meredekségéből (17) alapján meghatározhatjuk a Hall-effektust jellemző Hall-állandót
meredekségéből (17) alapján meghatározhatjuk a Hall-effektust jellemző Hall-állandót
![\[ R_H = \frac{M_H d}{I}\]](/images/math/4/c/3/4c35d5ddc60bb07265a738668eb3ad20.png)
ennek ismeretében pedig a töltéshordozó-koncentrációt:
![\[ n = \frac{1}{q R_H}\]](/images/math/4/5/4/45409755405c87ea8d7e308bbb19e2f1.png)
A Hall feszültség előjelét meghatározva, a mintán folyó áram és a mágneses tér irányának ismeretében meghatározható a töltéshordozó töltésének előjele is, vagyis eldönthető, hogy a mintában a többségi töltéshordozók elektronok vagy lyukak.
Egyetlen töltéshordozó esetén a töltéshordozó mozgékonysága – a 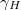 , ún. Hall-mozgékonyság – is meghatározható, hiszen az (5) és (16) egyenletek felhasználásával azt kapjuk, hogy
, ún. Hall-mozgékonyság – is meghatározható, hiszen az (5) és (16) egyenletek felhasználásával azt kapjuk, hogy
. (20)
Itt  az anyag mágneses tér nélkül mért vezetőképessége,
az anyag mágneses tér nélkül mért vezetőképessége, 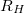 pedig a már ismertnek feltételezett Hall-állandó.
Ha a szennyezéses vezetés tartományában a félvezetőben létrejött Hall-feszültséget állandó áram és állandó mágneses indukció mellett a hőmérséklet függvényében vizsgáljuk, akkor azt találjuk, hogy a hőmérséklet emelkedésével a Hall-feszültség csökken. Ennek oka az, hogy ilyenkor a töltéshordozó-koncentráció növekszik, de mivel az áram állandó, (3) szerint a töltéshordozók átlagos sebességének, és így a (14) összefüggés értelmében
pedig a már ismertnek feltételezett Hall-állandó.
Ha a szennyezéses vezetés tartományában a félvezetőben létrejött Hall-feszültséget állandó áram és állandó mágneses indukció mellett a hőmérséklet függvényében vizsgáljuk, akkor azt találjuk, hogy a hőmérséklet emelkedésével a Hall-feszültség csökken. Ennek oka az, hogy ilyenkor a töltéshordozó-koncentráció növekszik, de mivel az áram állandó, (3) szerint a töltéshordozók átlagos sebességének, és így a (14) összefüggés értelmében  -nak is csökkennie kell. (A töltéshordozó-koncentráció változásának ez a hatása egyébként közvetlenül kiolvasható a (15) egyenletből). Ha a hőmérséklet emelésével eljutunk a sajátvezetés tartományába, akkor az azonos mennyiségben jelenlévő – ellenkező előjelű – kétféle töltéshordozó (elektron és lyuk) egymás Hall-feszültségét lerontja. A Hall-feszültség azonban mégsem lesz nulla, mert az elektronok és lyukak mozgékonysága nem azonos: a (lecsökkent) Hall-feszültség előjelét ilyenkor a nagyobb átlagos sebességgel mozgó, tehát a nagyobb mozgékonyságú töltéshordozó szabja meg.
-nak is csökkennie kell. (A töltéshordozó-koncentráció változásának ez a hatása egyébként közvetlenül kiolvasható a (15) egyenletből). Ha a hőmérséklet emelésével eljutunk a sajátvezetés tartományába, akkor az azonos mennyiségben jelenlévő – ellenkező előjelű – kétféle töltéshordozó (elektron és lyuk) egymás Hall-feszültségét lerontja. A Hall-feszültség azonban mégsem lesz nulla, mert az elektronok és lyukak mozgékonysága nem azonos: a (lecsökkent) Hall-feszültség előjelét ilyenkor a nagyobb átlagos sebességgel mozgó, tehát a nagyobb mozgékonyságú töltéshordozó szabja meg.
A mérőberendezés használata
A méréshez használt germánium lapka az 5.ábrán látható panelen van ragasztással rögzítve. A hozzávezetések banánhüvelyes csatlakozásban végződnek. A fűtést a szendvicsszerkezet belső felületén kialakított maratott fémréteg (fűtőszál) biztosítja. A hőmérsékletet mérő termoelem „meleg” pontja a lapkánál van, a „hideg” pont a csatlakozó banánhüvely és a hozzávezető fém érintkezési pontja. Mivel ez a pont a hordozó műanyag lapon van, fűtésnél kis mértékben melegszik. Ez befolyásolhatja a mérések eredményeit.
A mérés során a hordozó panelt egy tartó nyél segítségével (ami egyben tartalmazza a fűtés bevezetésének csatlakozó pontjait is ) úgy helyezzük az elektromágnes légrésébe, hogy a germánium lapka a vasmag közepénél legyen.
A mintára egyenfeszültséget kapcsolunk vagy egyenáramot folyatunk át, amit egy Hameg tápegység biztosít. Adott feladatban az átfolyó áramot külön multiméterrel mérjük és szükség szerint utána állítjuk, ha a külső paraméterek változása miatt az megváltozik.
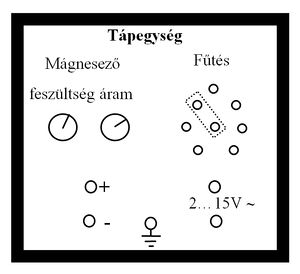
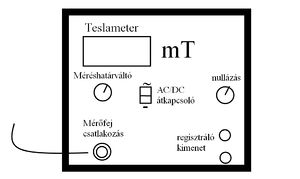
A mágneses teret a tápegység (6.ábra) egyenáramú részével táplált tekercsek hozzák létre. A mérés során a feszültségkapcsolót célszerű a legnagyobb értékre (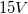 ) állítani és a mágneses teret (a mágnesező áramot) az áramszabályzó gombbal szabályozni (ekkor ugyanis a tápegység áramgenerátorként működik, így a tekercs esetleges ellenállás-változása a mágnesező áramot nem befolyásolja). A mágneses indukció értékét egy – a Hall-effektuson alapuló – mérőszonda, a hozzá csatlakozó mérőegység (7.ábra) segítségével határozzuk meg (a berendezést Teslameternek nevezik).
) állítani és a mágneses teret (a mágnesező áramot) az áramszabályzó gombbal szabályozni (ekkor ugyanis a tápegység áramgenerátorként működik, így a tekercs esetleges ellenállás-változása a mágnesező áramot nem befolyásolja). A mágneses indukció értékét egy – a Hall-effektuson alapuló – mérőszonda, a hozzá csatlakozó mérőegység (7.ábra) segítségével határozzuk meg (a berendezést Teslameternek nevezik).
A minta melegítése a tápegység váltófeszültségű oldalán található két alsó csatlakozóhüvelyből (6.ábra) vett árammal történik a fűtőszálban fejlődő hő segítségével. A fűtőfeszültséget úgy változtathatjuk, hogy a rövidre záró dugasszal a váltóáramú oldal bal felső részén található megfelelő hüvelyt a középső hüvellyel összekötjük. A minta hőmérsékletét Cu/CuNi termoelemmel és a hozzá kapcsolt Hameg feszültségmérővel mérjük. A termoelem hőmérsékleti együtthatója 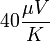 , a referenciahőmérséklet a szobahőmérséklet. A Hall-feszültség mérésére szintén egy Hameg multiméter szolgál.
, a referenciahőmérséklet a szobahőmérséklet. A Hall-feszültség mérésére szintén egy Hameg multiméter szolgál.
Mérési feladatok
- Mérje meg szobahőmérsékleten a mintában a Hall-feszültséget (
 ) a mintán átfolyó áram (
) a mintán átfolyó áram ( ) függvényében
) függvényében 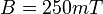 mágneses indukciónál. Az áramot
mágneses indukciónál. Az áramot  és
és 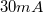 között
között 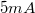 -enként változtassa, az áram bevezetéséhez a mintatartó panel AB pontjait használja. A mérést végezze el mindkét áramirány esetén. Az eredményeket ábrázolja
-enként változtassa, az áram bevezetéséhez a mintatartó panel AB pontjait használja. A mérést végezze el mindkét áramirány esetén. Az eredményeket ábrázolja 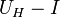 grafikonon.
grafikonon.
- Az Ohm-törvény alapján mérje meg a minta ellenállásának változását a mágneses indukció függvényében szobahőmérsékleten,
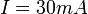 áramnál. (Árambevezetés az AB pontokon, a mintán eső feszültség mérése szintén. Ha a mérés folyamán változik a beállított
áramnál. (Árambevezetés az AB pontokon, a mintán eső feszültség mérése szintén. Ha a mérés folyamán változik a beállított 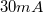 -es áram értéke, akkor a meghajtó feszültség finom állításával korrigáljuk.) Ábrázolja az
-es áram értéke, akkor a meghajtó feszültség finom állításával korrigáljuk.) Ábrázolja az 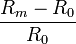 relatív ellenállás-változást a mágneses indukció függvényében. A mágneses indukciót
relatív ellenállás-változást a mágneses indukció függvényében. A mágneses indukciót 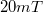 lépésekben
lépésekben  és
és 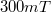 között változtassa.
között változtassa.
- Mágneses tér nélkül mérje meg a minta ellenállásának hőmérsékletfüggését 175 0C és szobahőmérséklet között (8-9 pontban),
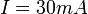 áramnál. (Árambevezetés az AB pontokon, a mintán eső feszültség mérése szintén. Ha a mérés folyamán változik a beállított
áramnál. (Árambevezetés az AB pontokon, a mintán eső feszültség mérése szintén. Ha a mérés folyamán változik a beállított 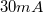 -es áram értéke, akkor a meghajtó feszültség finom állításával korrigáljuk.). Az ellenállásértékekből számítsa ki a vezetőképességet (
-es áram értéke, akkor a meghajtó feszültség finom állításával korrigáljuk.). Az ellenállásértékekből számítsa ki a vezetőképességet (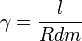 , ahol
, ahol 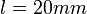 ,
, 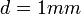 ,
, 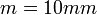 ), és vegye fel az
), és vegye fel az 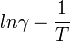 grafikont. A grafikon egyenes szakaszából – amely a sajátvezetés tartományába esik – határozza meg a Ge tilos sáv-szélességét, értékét '
grafikont. A grafikon egyenes szakaszából – amely a sajátvezetés tartományába esik – határozza meg a Ge tilos sáv-szélességét, értékét '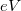 -ban és
-ban és 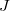 -ban is adja meg.
-ban is adja meg.
- A Hall-feszültség mágneses tér nélkül végrehajtott nullázása után, mérje meg szobahőmérsékleten a Hall-feszültségnek a mágneses indukciótól való függését a tér két ellentétes irányítása mellett,
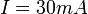 áramnál. A Hall-feszültség nullázásához vegye ki a mágnes két vasmagját és a mintára adott árammal állítsa be a nulla feszültségértéket. A
áramnál. A Hall-feszültség nullázásához vegye ki a mágnes két vasmagját és a mintára adott árammal állítsa be a nulla feszültségértéket. A 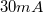 –es áramot ehhez az értékhez adja hozzá! (Árambevezetés az AB pontokon, a mintán eső feszültség mérése szintén. Ha a mérés folyamán változik a beállított
–es áramot ehhez az értékhez adja hozzá! (Árambevezetés az AB pontokon, a mintán eső feszültség mérése szintén. Ha a mérés folyamán változik a beállított 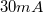 -es áram értéke, akkor a meghajtó feszültség finom állításával korrigáljuk.) A mágneses indukciót
-es áram értéke, akkor a meghajtó feszültség finom állításával korrigáljuk.) A mágneses indukciót  és
és 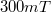 között,
között, 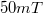 lépésekben változtassa. Az eredményeket ábrázolja
lépésekben változtassa. Az eredményeket ábrázolja 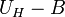 grafikonon. Határozza meg a Hall-állandót, a töltéshordozó típusát, a töltéshordozó-koncentrációt és a töltéshordozók mozgékonyságát.
grafikonon. Határozza meg a Hall-állandót, a töltéshordozó típusát, a töltéshordozó-koncentrációt és a töltéshordozók mozgékonyságát.
-
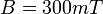 mágneses indukció és
mágneses indukció és 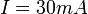 áram mellett mérje ki a Hall-feszültség hőmérsékletfüggését a hőmérsékletet szobahőmérsékletről lassan kb. 170 0C-ra emelve (15-20 mérési pontban). Az eredményeket ábrázolja és értékelje.
áram mellett mérje ki a Hall-feszültség hőmérsékletfüggését a hőmérsékletet szobahőmérsékletről lassan kb. 170 0C-ra emelve (15-20 mérési pontban). Az eredményeket ábrázolja és értékelje.
A mérések során ügyeljünk a következőkre:
|
Irodalom
Budó Ágoston–Mátrai Tibor: Kísérleti fizika II.
PDF formátum