Millikan-kísérlet és szimuláció
Szerkesztés alatt!
Tartalomjegyzék
|
Elméleti összefoglaló
Történeti áttekintés
Elektromos jelenségekről először a görögök számoltak be, amikor feljegyezték, hogy a megdörzsölt borostyán a könnyű tárgyakat magához vonzza. E jelenséget 1747-ben Benjamin Franklin azzal magyarázta, hogy minden anyagban bizonyos mennyiségű elektromos folyadék vagy tűz található, mely folyadék többlete pozitív, hiánya eddig negatív töltést eredményez. Symmer tizenkét évvel későbbi elmélete szerint a semleges állapotban lévő anyag azért nem mutat elektromos tulajdonságokat, mert a pozitív ill. negatív elektromosságért felelős súlytalan folyadékokból azonos mennyiséget foglal magába.
Franklin már olyan elektromos részecske létezését tételezte fel, mely elegendően kicsi ahhoz, hogy könnyen behatoljon az anyagba. Kísérletei, melyek szerint elektrolízis közben az ellentétes elektródokon kiváló vegyületek tömege arányos kémiai egyenérték-súlyukkal, támogatták ezt a hipotézist. A folyadékelmélet és az az elképzelés, mely szerint az elektromosság az anyag mechanikai feszültségi állapota, a XIX. század végéig az elektromos jelenségek kizárólagos magyarázata maradt.
Az elektromosság azon természetes egységének megnevezésére, melynek hatására valamely elektródon egy atomnyi hidrogén vagy más egyértékűanyag szabadul fel, G. J. Stoney az “elektron” kifejezést javasolta 1891-ben.
Az egyszeres iontöltés meghatározását Townsend kísérelte meg először az 1890-es évek végén. Megfigyelte, hogy kénsav elektrolízise során pozitív töltésű hidrogén és oxigén szabadul fel. A felszabaduló ionizált gázt vízen átbuborékoltatva ködöt képzett. Feltételezte, hogy a telített vízgőzben minden ion nedvességet kondenzál maga körül, vagyis az ionok száma megegyezik a cseppekével.
Townsend eredményei a 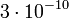 e.s.u. (e.s.u.:egykori elektrosztatikus egység) nagyságrendbe estek. J.J Thompson 1900-ban egy a Townsendéhez hasonló módszerrel
e.s.u. (e.s.u.:egykori elektrosztatikus egység) nagyságrendbe estek. J.J Thompson 1900-ban egy a Townsendéhez hasonló módszerrel 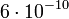 e.s.u. értéket kapott. Minthogy a feltevés, hogy cseppek egy iont tartalmaznak, csak közelítőleg bizonyult helyesnek, ezek a módszerek nem voltak alkalmasak az elektrontöltés pontos meghatározására.
e.s.u. értéket kapott. Minthogy a feltevés, hogy cseppek egy iont tartalmaznak, csak közelítőleg bizonyult helyesnek, ezek a módszerek nem voltak alkalmasak az elektrontöltés pontos meghatározására.
H.S. Wilson Townsend és Thompson kísérleteit úgy tökéletesítette, hogy a két lapos rézelektróda között állított elő ködöt. A töltetlen ill. 2000 V feszültségre kapcsolt lemezek között megfigyelve a ködcseppek esési sebességét, és kihasználva, hogy a két sebesség arányos a cseppekre ható erőkkel, Wilson meghatározta az elektron töltését, mely 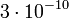 e.s.u értékűnek adódott. Mivel Wilson mérései a köd felső részére ill. a legkisebb töltésű cseppekre vonatkoztak (a nagyobb töltésű cseppek az elektromos térben gyorsabban mozogtak lefelé), eredményei összhangban voltak a cseppenkénti egy ion feltevéssel.
e.s.u értékűnek adódott. Mivel Wilson mérései a köd felső részére ill. a legkisebb töltésű cseppekre vonatkoztak (a nagyobb töltésű cseppek az elektromos térben gyorsabban mozogtak lefelé), eredményei összhangban voltak a cseppenkénti egy ion feltevéssel.
Millikan tovább javította Wilson elrendezését azzal, hogy a lemezekre nagyobb feszültséget kapcsolt, aminek következtében a cseppek esési sebessége nemcsak csök-kent, hanem esetenként meg is fordult. Egyes töltött cseppek felfelé mozogtak, mások gyorsan lefelé, míg a töltetlen cseppek változatlan sebességgel haladtak lefelé. Néhány csepp, amely akkora töltést hordozott, hogy a gravitációs erőt a cseppre ható elektromos erő csaknem kiegyenlítette, a látómezőben maradt. A lemezekre kapcsolt feszültség változtatásával Millikan kiegyensúlyozta ezen cseppeket, ami lehetővé tette, hogy egyetlen cseppen végezzen méréseket. Ezzel a módszerrel tanulmányozta az egyes ionok tulajdonságait, és vizsgálta, hogy a különböző ionok azonos a töltést hordoznak-e.
Az elektron töltésének meghatározása
A részecskék által hordozott elektromos töltés meghatározható, ha ismert nagyságú elektromos térben mérjük a részecskére ható erőt. Bár a megfelelő elektromos tér előállítása viszonylag egyszerű, az egy vagy néhány többletelektront hordozó részecskékre ható erő igen kicsi. Például egy 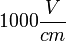 erősségű tér
erősségű tér 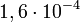 N erővel hat az egyetlen többlet elektronnal rendelkező részecskére, ami egy
N erővel hat az egyetlen többlet elektronnal rendelkező részecskére, ami egy 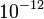 g tömegű részecskére ható gravitációs erővel mérhető össze.
Millikan kísérletének sikere attól függött, hogy tudnak-e ilyen nagyságrendű erőt mérni.
g tömegű részecskére ható gravitációs erővel mérhető össze.
Millikan kísérletének sikere attól függött, hogy tudnak-e ilyen nagyságrendű erőt mérni. 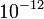 g vagy kisebb tömegű olajcseppek viselkedését vizsgálták gravitációs és elektromos térben. A levegőben eső csepp sebességének mérése a Stokes-törvény alkalmazásával lehetővé teszi a csepp tömegének meghatározását, míg az elektromos térben emelkedő csepp sebességéből a cseppre ható er őre, ill. a hordozott töltésre következtethetünk.
Bár ez a módszer lehetővé teszi egyetlen csepp töltésének vizsgálatát, csak a mért adatok elemzésével és némi kísérleti jártassággal lehetünk képesek egyetlen elektron töltésének meghatározására. A lassan eső vagy emelkedő cseppek csak kisszámú többlet elektront hordoznak. Mozgásuk megfigyelése alapján töltésük meghatározható,ami lehetővé teszi annak vizsgálatát, hogy a cseppek töltése egy elemi töltés egészszámú többszöröseként áll-e elő, ahogy azt az elektromos töltés kvantált természete alapján várjuk. Ha minden méréséhez más cseppet használunk, felmerül a kérdés, hogy milyen hatással van a töltésre maga a csepp. Ez a bizonytalanság kiküszöbölhet ő, ha ionizáló forrás alkalmazásával egyazon csepp töltését változtatjuk a megfigyelés során. Ha az eredményül kapott töltések valamely érték egészszámú többszörösei, akkor az elemi elektromos töltés létezését egyértelműen bizonyítottuk.
Az elektron töltésének ismeretében lehetőség nyílik az Avogadro-szám meghatározására is. Elektrolízis során az egy mólnyi mennyiség leválasztásához szükséges töltés (Faraday) egyenlő az elektron töltés és az Avogadro-szám szorzatával. Az elektrolízis kísérletekből adódóan
g vagy kisebb tömegű olajcseppek viselkedését vizsgálták gravitációs és elektromos térben. A levegőben eső csepp sebességének mérése a Stokes-törvény alkalmazásával lehetővé teszi a csepp tömegének meghatározását, míg az elektromos térben emelkedő csepp sebességéből a cseppre ható er őre, ill. a hordozott töltésre következtethetünk.
Bár ez a módszer lehetővé teszi egyetlen csepp töltésének vizsgálatát, csak a mért adatok elemzésével és némi kísérleti jártassággal lehetünk képesek egyetlen elektron töltésének meghatározására. A lassan eső vagy emelkedő cseppek csak kisszámú többlet elektront hordoznak. Mozgásuk megfigyelése alapján töltésük meghatározható,ami lehetővé teszi annak vizsgálatát, hogy a cseppek töltése egy elemi töltés egészszámú többszöröseként áll-e elő, ahogy azt az elektromos töltés kvantált természete alapján várjuk. Ha minden méréséhez más cseppet használunk, felmerül a kérdés, hogy milyen hatással van a töltésre maga a csepp. Ez a bizonytalanság kiküszöbölhet ő, ha ionizáló forrás alkalmazásával egyazon csepp töltését változtatjuk a megfigyelés során. Ha az eredményül kapott töltések valamely érték egészszámú többszörösei, akkor az elemi elektromos töltés létezését egyértelműen bizonyítottuk.
Az elektron töltésének ismeretében lehetőség nyílik az Avogadro-szám meghatározására is. Elektrolízis során az egy mólnyi mennyiség leválasztásához szükséges töltés (Faraday) egyenlő az elektron töltés és az Avogadro-szám szorzatával. Az elektrolízis kísérletekből adódóan 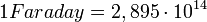 e.s.u., mely értéket az elektron töltésével (
e.s.u., mely értéket az elektron töltésével (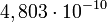 e.s.u.) osztva megkapjuk az Avogadro-számot.
e.s.u.) osztva megkapjuk az Avogadro-számot.
Egy csepp töltésének számítása
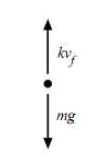
A csepp által hordozott töltés számításához vizsgáljuk meg, milyen erők hatnak egy olajcseppre. Az (1.ábra) az állandósult sebességgel eső cseppre ható erők láthatóak. (A kísérletben használt cseppek néhány  s alatt elérik végsebességüket.) Az (1.ábra)
s alatt elérik végsebességüket.) Az (1.ábra)  az esési sebesség,
az esési sebesség, a súrlódási együttható a levegő és a csepp között,
a súrlódási együttható a levegő és a csepp között,  a csepp tömege és g a nehézségi gyorsulás. Mivel az erők egyenlők és ellentétes irányúak:
a csepp tömege és g a nehézségi gyorsulás. Mivel az erők egyenlők és ellentétes irányúak:
![\[ m g =k v_{f} \]](/images/math/0/8/9/089d66c99838f09c0cec47d1915f6238.png)
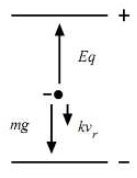
A (2.ábra) az elektromos tér hatására emelkedő cseppre ható erőket mutatja. az elektromos térerősség,
az elektromos térerősség, 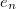 a csepp által hordozott töltés és
a csepp által hordozott töltés és 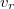 az emelkedés sebessége. Az erőket vektoriálisan összegezve:
az emelkedés sebessége. Az erőket vektoriálisan összegezve:
![\[E e_{n} = m g + k v_{f} \]](/images/math/b/9/7/b972c0df811628b6f0c9b798b6eb3b75.png)
Mivel a levegő sűrűsége csak mintegy ezredrésze az olajénak, a levegő felhajtóerejét elhanyagoltuk. Az (1) és (2) egyenletekből  -t kiküszöbölve és
-t kiküszöbölve és 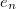 -re
megoldva:
-re
megoldva:
![\[ e_{n}=m g \frac{v_f+v_r}{E v_f} \]](/images/math/e/f/4/ef4b42c01590ddfad060199487fda3dc.png)
ahol
![\[ m = \frac{4}{3}\pi r^{3} \sigma \]](/images/math/2/a/d/2adb72b6d940dc3b6a71aa1afb95ae81.png)
míg r a csepp sugara,  pedig az olaj sűrűsége. A csepp sugarát az
pedig az olaj sűrűsége. A csepp sugarát az  viszkozitású folyadékban eső gömb alakú test sugara és sebessége közötti kapcsolatot megadó Stokes-törvény alapján a
viszkozitású folyadékban eső gömb alakú test sugara és sebessége közötti kapcsolatot megadó Stokes-törvény alapján a
![\[r = \left[ \frac{9 \eta v_f}{2 g (\sigma - \rho)} \right] ^{1/2}\]](/images/math/8/c/6/8c68d732d35fc09e6e9f0884b4d9f2d2.png)
összefüggés szerint számítjuk, ahol  a közeg sűrűsége. A (4) és (5) egyenleteket (3) -ba helyettesítve és figyelembe véve, hogy az olaj sűrűsége sokkal nagyobb mint a levegőé (
a közeg sűrűsége. A (4) és (5) egyenleteket (3) -ba helyettesítve és figyelembe véve, hogy az olaj sűrűsége sokkal nagyobb mint a levegőé ( ):
):
![\[e_n = \left( \frac{4 \pi}{3}\right) \left[ \frac{\left( \frac{9 \eta}{2}\right)^{3}.}{g \sigma} \right] ^{1/2} \frac{\left(v_f+v_r\right)\left(v_f\right)^{1/2}.}{E}\]](/images/math/8/c/c/8cc037cb1d47cb1aaddeeaaafacebd50.png)
A Stokes-törvény azonban csak addig érvényes, míg a csepp sebessége nagyobb mint 0,1 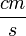 . (Az ilyen és kisebb sebességű cseppek 2
. (Az ilyen és kisebb sebességű cseppek 2 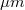 nagyságrendű átmérője összemérhető a levegő molekulák szabad úthosszával, amely esetben a Stokes-törvény érvényességének egyik alapfeltétele nem teljesül.) Mivel a cseppek tipikus sebessége kísérletünkben a 0,01 - 0,001
nagyságrendű átmérője összemérhető a levegő molekulák szabad úthosszával, amely esetben a Stokes-törvény érvényességének egyik alapfeltétele nem teljesül.) Mivel a cseppek tipikus sebessége kísérletünkben a 0,01 - 0,001 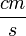 tartományba esik,egy
tartományba esik,egy
![\[ \left[ \frac{1}{1+\left( \frac{b}{pr}\right)}\right]^{3/2}\]](/images/math/5/1/2/512edd9b994a8fe8990ec9d08b018052.png)
alakú korrekciós tényező bevezetése szükséges, ahol  állandó,
állandó,  a légköri nyomás,
a légköri nyomás,  pedig a Stokes-törvényből számolt csepp sugár.
Az elektromos térerősség
pedig a Stokes-törvényből számolt csepp sugár.
Az elektromos térerősség 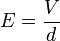 ahol
ahol  a
a  távolságban lévő párhuzamos lemezek közötti potenciálkülönbség. Ezt és (7)-et a (6) egyenletbe helyettesítve:
távolságban lévő párhuzamos lemezek közötti potenciálkülönbség. Ezt és (7)-et a (6) egyenletbe helyettesítve:
![\[e_n = \{\frac{4\pi d}{3}\left[\frac{\left(\frac{9\eta}{2}\right)^3}{g\sigma}\right]^{\frac{1}{2} }\} \times \{\left[ \frac{1}{1+\frac{b}{pr} } \right]^{\frac{3}{2} } \} \times \{ \frac{(\nu_f+\nu_r)\nu_f^{\frac{1}{2} } }{V} \}\]](/images/math/a/0/e/a0eb5c994a507bb29544bf5edaa2207c.png)
Az első szorzófaktorban lévő mennyiségek állandók, a másodikban a csepp sugara, míg a harmadikban a mérendő sebességek szerepelnek. A fenti egyenletekben előforduló mennyiségek és mértékegységeik a következők:
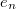 - a csepp által hordozott töltés
- a csepp által hordozott töltés 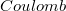 -ban,
-ban,
 - a kondenzátor lemezei közötti távolság
- a kondenzátor lemezei közötti távolság  -ben,
-ben,
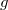 - a nehézségi gyorsulás
- a nehézségi gyorsulás 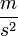 -ben,
-ben,
 - a levegő viszkozitása
- a levegő viszkozitása 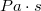 -ban,
-ban,
 - a levegő sűrűsége
- a levegő sűrűsége 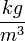 -ben,
-ben,
 - az olaj sűrűsége
- az olaj sűrűsége 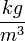 -ben,
-ben,
 - állandó,
- állandó, 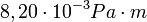 ,
,
 - a légköri nyomás
- a légköri nyomás 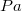 -ban,
-ban,
 - a csepp sugara
- a csepp sugara  -ben,
-ben,
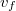 - az esési sebesség
- az esési sebesség 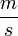 -ban,
-ban,
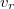 - az emelkedési sebesség
- az emelkedési sebesség 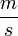 -ban,
-ban,
 - a potenciálkülönbség a lemezek között
- a potenciálkülönbség a lemezek között  -ban.
-ban.
A mérőeszköz és előkészítése
A méréshez használt készlet (3.ábra) a mérőberendezésből, a hozzá kapcsolt töltő kapcsolóból (plate charging switch), a halogén fényforráshoz való 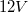 -os egyenáramú adapterből (DC power adaptor), egy flakon nem párolgó olajból (sűrűsége
-os egyenáramú adapterből (DC power adaptor), egy flakon nem párolgó olajból (sűrűsége 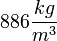 ), és a porlasztóból (atomizer) áll.
), és a porlasztóból (atomizer) áll.
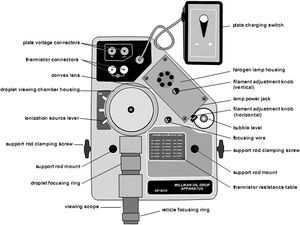
A mérőberendezés részei (4.ábra):
- megfigyelő kamra (droplet viewing chamber),
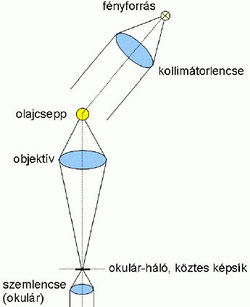
- megfigyelő mikroszkóp (5. ábra, viewing scope; 30-szoros nagyítás, megvilágított képmező, egyenesállású kép) okulár-hálóval (vonaltávolságok: nagy osztás
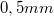 , kis osztás
, kis osztás 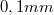 ), okulár fókuszáló gyűrűvel és csepp fókuszáló gyűrűvel (reticle & droplet focusing rings),
), okulár fókuszáló gyűrűvel és csepp fókuszáló gyűrűvel (reticle & droplet focusing rings),
- fókuszáló huzal (focusing wire; a megfigyelő mikroszkóp beállításához),
- lemez feszültség csatlakozók (plate voltage connectors),
- termisztor csatlakozók (thermistor connectors; a termisztorok az alaplemezbe vannak beépítve).
| FIGYELEM: A termisztor csatlakozóira ne kapcsoljunk feszültséget! |
- termisztor táblázat (thermistor resistance table; ellenállás a hőmérséklet függvényében)
- három állású ionizáló forrás kar (ionization source lever; BE, KI és Csepp porlasztás)
- szintező (bubble level)
- 3 szintező láb
- lemez töltő kapcsoló (plate charging switch;
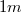 kábellel, hogy a kapcsoló működtetése ne zavarja a mérést)
kábellel, hogy a kapcsoló működtetése ne zavarja a mérést)
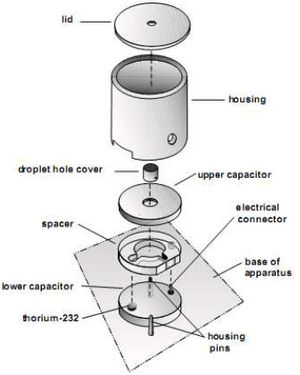
A megfigyelő kamra részei (6.ábra):
- fedő (lid)
- ház (housing)
- csepp furat fedő (drop hole cover)
- felső kondenzátor lemez (upper capacitor)
- műanyag távtartó (kb.
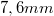 vastag)
vastag)
- alsó kondenzátor lemez (lower capacitor)
- tórium-232 alfa-forrás (
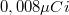 )
)
- elektromos csatlakozás a felső kondenzátor lemezhez
- tórium-232 alfa-forrás (
- konvex lencsék
Megjegyzés: A tórium-232 természetesen előforduló, 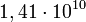 év felezési idejű, kis aktivitású alfa-részecske forrás. Használata nem jelent veszélyt a kísérletet végző személyre.
év felezési idejű, kis aktivitású alfa-részecske forrás. Használata nem jelent veszélyt a kísérletet végző személyre.
A mérés elvégzéséhez szükséges további eszközök
- nagyfeszültségű szabályozott tápegység (max.
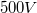 , min.
, min. 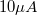 )
)
- digitális multiméter (feszültség- és ellenállás méréséhez)
- mérővezetékek banándugókkal (4 db)
- stopper
5568i kép
Az optikai rendszer beállítása:
A megfigyelő mikroszkóp fókuszálása:
- Helyezzük vissza a műanyag távtartó lemezt és a felső kondenzátor lemezt az alsó kondenzátor lemezre. Helyezzük vissza a burkolatot, hogy az illesztő csapok az alap megfelelő furataiba illeszkedjenek (lásd 6.ábra).
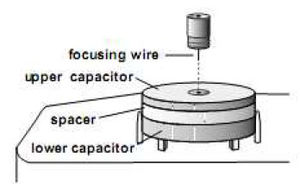
- Csavarjuk ki a fókuszáló huzalt a tárolási helyéről és gondosan illesszük a felső kondenzátor lemez közepén lévő nyílásba (7.ábra).
- Csatlakoztassuk a
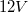 -os transzformátor dugaszát a halogén-lámpa burkolatának csatlakozójába és dugaszoljuk az elosztó csatlakozóba.
-os transzformátor dugaszát a halogén-lámpa burkolatának csatlakozójába és dugaszoljuk az elosztó csatlakozóba.
- A háló fókuszáló (okulár) gyűrű segítségével állítsuk élesre az okulár-hálót.
- Figyeljük meg a fókuszáló huzalt a megfigyelő mikroszkópon keresztül, és állítsuk élesre a csepp fókuszáló gyűrű segítségével.
A halogén izzószál fókuszálása:
- Forgassuk az izzószál vízszintes beállító gombját. A fény akkor a legjobban fókuszált, amikor a fókuszáló huzal jobboldali éle a legfényesebb (a legnagyobb a kontraszt a huzal közepéhez képest).
- A fókuszáló huzalt a mikroszkópon át figyelve addig forgassuk az izzószál függőleges beállító gombját, míg a fókuszáló huzalra eső fény a legerősebb nem lesz.
- Helyezzük vissza a fókuszáló huzalt a tárolási helyére.
A kezelőszervek funkciói:
Ionizáló forrást szabályozó kar (8.ábra):
- A kar KI (OFF) állása esetén, az ionizáló forrás minden oldalról árnyékolva van, s így nem kerülhetnek alfa-részecskék a cseppek környezetébe.
- BE (ON) állásban nincs árnyékolás, a tórium-232 forrásból ionizáló alfa-részecskék jutnak a cseppek környezetébe.
- A CSEPP PORLASZTÁS (SPRAY DROPLET) helyzetben a kamra egy levegőző furaton keresztül szellőzik. A porlasztásnál befújt levegő ezen keresztül távozik.
Lemez töltő kapcsoló
A lemez töltő kapcsoló három állású:
- TOP PLATE -: a feszültségforrás negatív csatlakozási pontja a felső lemezzel van összeköttetésben.
- TOP PLATE +: a feszültségforrás negatív csatlakozási pontja az alsó lemezzel van összeköttetésben.
- PLATES GROUNDED: a lemezek le vannak kapcsolva a feszültségforrásról és össze vannak kötve egymással.
A feszültség beállítása és mérése:
- Csatlakoztassuk a nagyfeszültségű DC tápegységet a lemez feszültség csatlakozókhoz banándugós vezetékekkel és állítsunk be kb.
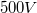 -ot.
-ot.
- Digitális multiméterrel mérjük meg a kondenzátor lemezekre adott feszültséget a lemez feszültség csatlakozókon. A lemezekkel egy-egy
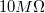 nagyságú ellenállás van sorba kapcsolva a véletlen áramütések megakadályozása céljából.
nagyságú ellenállás van sorba kapcsolva a véletlen áramütések megakadályozása céljából.
A kamra hőmérsékletének meghatározása
Csatlakoztassuk a multimétert a termisztor csatlakozókhoz és mérjük meg a termisztor ellenállását, melyből az alapon elhelyezett Termisztor Ellenállás Táblázat segítségével az alsó kondenzátor-lemez hőmérséklete meghatározható. Ez az érték jól közelíti a megfigyelő kamrán belüli hőmérsékletet. Bár a dikroikus ablakok a halogén izzó által keltett hő legnagyobb részét visszaverik, a megfigyelő kamrán belül a hőmérséklet hosszabb megvilágítás során emelkedhet. Ezért célszerű a kamra hőmérsékletét ~15 percenként ellenőrizni.
A kísérlet végrehajtása
- Helyezzük vissza a csepp nyílás fedelét a felső kondenzátor lemezre, majd tegyük helyére a burkolat fedelét (lásd 6.ábra).
- Mérjük meg a lemez feszültséget és a termisztor ellenállást (hőmérséklet).
Megjegyzés: A csepp-nyílás fedele megakadályozza, hogy további cseppek kerüljenek a megfigyelő kamrába.
A cseppek bevitele a megfigyelő kamrába
- Töltsük meg a porlasztót nem párolgó olajjal (pl. Squibb #5597 Mineral Oil, sűrűség:
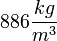 ).
).
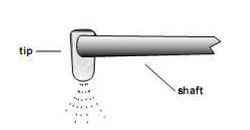
- A porlasztó pumpa többszöri gyors megnyomásával, készítsük elő a porlasztót. Győződjünk meg arról, hogy a porlasztó csúcs lefelé mutat a tengelyre merőlegesen (lásd 9.ábra).
- Helyezzük az ionizáló forrás karját a Csepp Porlasztás Helyzetbe (Spray Droplet Position), hogy a cseppeknek a kamrába bevitele során levegő távozhasson a kamrából.
- Helyezzük a porlasztó csúcsát a megfigyelő kamra fedelén lévő nyílásba.
- A mikroszkópon keresztül figyelve, egyszer gyorsan nyomjuk meg a porlasztó pumpát. Ezzel visszük be az apró olajcseppeket a felső kamrába. Ezután a porlasztó pumpa lassú megnyomásával kényszerítsük át a cseppeket a felső kondenzátor lemezben lévő csepp bevezető furaton keresztül a két kondenzátor lemez közötti térbe.
- Amikor cseppek "záporoznak" a megfigyelő mikroszkópon látóterében, állítsuk az ionizáló forrás karját KI (OFF) helyzetbe.
Megjegyzések:
- A cseppek bevezetésének pontos technikáját a kísérletezőnek kell kialakítania. A cél az, hogy ne ködöt hanem kis számú cseppet kapjunk, amelyek közül a megfelelő könnyen kiválasztható. A porlasztó túlzott működtetésével fölöslegesen sok csepp kerül a megfigyelési területre és, ami még fontosabb , a kamra fala és a megfigyelő mikroszkóp fókuszpontja közötti területre. Az utóbbiak gátolják a mikroszkóp fókuszpontjában lévő cseppek megfigyelését.
- Ha túl sok cseppet porlasztottunk be, várjunk három-négy percet, míg a többségük távozik a képmezőből, vagy szereljük szét a megfigyelő kamrát (a DC tápegység kikapcsolása után). Ha túl sok olaj halmozódott fel benne, a megfigyelő kamrát tisztítani kell. (Minél kevesebb olajat porlasztunk a kamrába, annál ritkábban kell tisztítani.)
A csepp kiválasztása
- A képmezőben látható cseppek közül válasszunk ki egyet, mely elektromos tér nélkül lassan (kb.
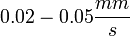 sebességgel) esik, és legalább egy - vagy + töltést hordoz (sebességet vált, amikor a lemezek töltöttek).
sebességgel) esik, és legalább egy - vagy + töltést hordoz (sebességet vált, amikor a lemezek töltöttek).
- Ha megtaláltuk a megfelelő méretű és töltésű olajcseppet, finoman állítsuk be a megfigyelő mikroszkóp fókuszát.
Megjegyzések:
- Egy csepp, amely elektromos tér nélkül ~15 s alatt teszi meg a két vastag rácsvonal közötti távolságot (
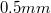 ),
), 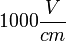 -es elektromos tér hatása alatt 1 többlet elektronnal
-es elektromos tér hatása alatt 1 többlet elektronnal 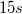 , 2 elektronnal
, 2 elektronnal 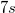 , ill. 3 elektronnal
, ill. 3 elektronnal 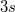 alatt emelkedik ugyanannyit. (Megjegyzés: ezek az arányok csak közelítőek.)
alatt emelkedik ugyanannyit. (Megjegyzés: ezek az arányok csak közelítőek.)
- Ha túl sok csepp van a képmezőben, a kondenzátor-lemezek feszültség alá helyezésével ritkítható számuk.
- Ha túl kevés töltött cseppet találunk, a megfelelő méretű és töltésű csepp előállításához ~5 másodpercre állítsuk az ionizáló forrás karját BE (ON) helyzetbe.
- A mikroszkóp megfelelő fókuszálása mellett az olajcseppek fénylő apró pontoknak látszanak.
Adatgyűjtés a cseppek emelkedése és esése során
- Mérjük meg a kiválasztott csepp emelkedési (a lemezek töltöttek) és esési (a lemezek nem töltöttek) sebességét kb. 10-20 esetben. A cseppek mozgatásához használjuk a lemez feszültség kapcsolót.
- Számítsuk ki a csepp töltését. Ha a csepp töltése az első meghatározáskor nagyobb, mint 5 többlet elektron, a további mérések során lassabban mozgó cseppeket használjunk.
- Vezessünk be további cseppeket a kamrába a korábban leírt eljárással és válasszunk ki egy másik cseppet.
- Mérjük a kiválasztott csepp emelkedési és esési sebességét kb. 10-20 esetben. Mozgását addig kövessük, amíg töltése spontán módon meg nem változik, vagy a csepp ki nem lép a képmezőből.
- Vigyük a cseppet a képmező tetejére és néhány másodpercre helyezzük az ionizáló forrás kart BE (ON) helyzetbe, miközben a csepp esik.
- Ha a csepp emelkedési sebessége megváltozik, mérjük meg az emelkedési sebességet ahányszor csak tudjuk (legfeljebb 20 mérés).
- Ha a csepp még a képmezőben van, próbáljuk megváltoztatni a csepp töltését még több alfa-részecske bevezetésével, az előbb leírt módon, és mérjük meg az új emelkedési sebességet 10-20 esetben, ha lehetséges.
- Ismételjük meg a 7. lépést ahányszor csak lehetséges.
- Jegyezzük fel a lemezek közötti feszültséget, az olaj sűrűségét, a levegő viszkozitását a megfigyelő kamra hőmérsékletét (lásd A. Függelék), és a légköri nyomást minden egyes sebességmérési sorozat esetében.
Megjegyzések:
- A legnagyobb mérési pontosságot akkor érhetjük el, ha az időt azon pillanatok között mérjük, amikor a fénylő csepp áthalad az első ill. a második vastag rácsvonal mögött. (Ezek a vonalak tárgysíkra vonatkoztatva
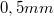 vannak egymástól.)
vannak egymástól.)
- Célszerű minél több különböző sebességet megfigyelni egyetlen cseppel.
A csepp töltésének számítása
A (8) egyenlet alapján. Az elektron töltésének elfogadott értéke 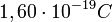 .
.
Mérési feladatok
- Határozza meg egy kiválasztott lassú és legalább egy - vagy + többlet elektron töltésű csepp emelkedési és esési sebességét kb. 10-20 esetben!
- Az ionizáló forrás segítségével változtassa meg a csepp töltését és ismételje meg az 1. feladatot!
- Határozza meg több másik kiválasztott csepp emelkedési és esési sebességét kb. 10-20 esetben!
- A mérési eredmények alapján állapítsa meg a cseppek által hordozott többlet elektronok számát és ábrázolja töltésük nagyságát a többlet elektronok számának függvényében! A legkisebb négyzetek módszerével határozza meg az elektron töltésének nagyságát!
Függelékek
A. Függelék
A levegő sűrűsége 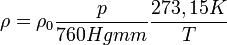 , ahol
, ahol 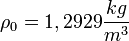 a levegő 0°C hőmérsékletre és
a levegő 0°C hőmérsékletre és 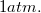 nyomásra vonatkozó értéke.
nyomásra vonatkozó értéke.
B. Függelék
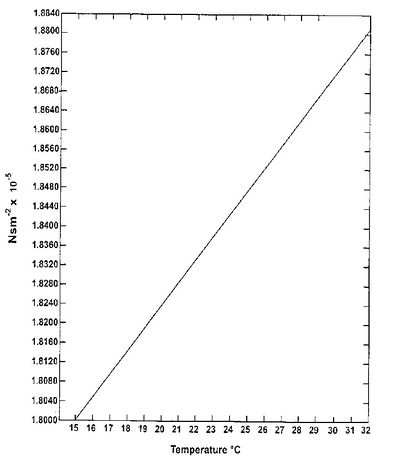
A száraz levegő viszkozitása a hőmérséklet függvényében:
C. Függelék
A Millikan kísérletben használt termisztor ellenállása a hőmérséklet függvényében:
Thermistor resistance table
| °C | 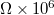
|
°C | 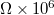
|
°C | 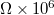
|
|---|---|---|---|---|---|
| 10 | 3.239 | 20 | 2.300 | 30 | 1.774 |
| 11 | 3.118 | 21 | 2.333 | 31 | 1.736 |
| 12 | 3.004 | 22 | 2.169 | 32 | 1.700 |
| 13 | 2.897 | 23 | 2.110 | 33 | 1.666 |
| 14 | 2.795 | 24 | 2.053 | 34 | 1.634 |
| 15 | 2.700 | 25 | 2.000 | 35 | 1.603 |
| 16 | 2.610 | 26 | 1.950 | 36 | 1.574 |
| 17 | 2.526 | 27 | 1.902 | 37 | 1.547 |
| 18 | 2.446 | 28 | 1.857 | 38 | 1.521 |
| 19 | 2.371 | 29 | 1.815 | 39 | 1.496 |
PDF formátum
Millikan-kísérlet és szimuláció(pdf)