Pásztázó alagútmikroszkóp (STM) alkalmazása
Szerkesztés alatt!
Tartalomjegyzék[elrejtés] |
Információk
A gyakorlatnak otthont adó intézmény:
MTA TTK MFA (Műszaki Fizikai és Anyagtudományi Kutatóintézet),Nanoszerkezetek Osztály
Helyszíne:
KFKI telephely (Csillebérc), Budapest XII., Konkoly-Thege M. út 29-33., 26-os épület, f.sz. 1-es labor.
Megközelítése:
Az egyetem északi részéről: 18-as villamossal a Széll Kálmán térig, onnan a 21-es busszal a végállomásig.
Az egyetem déli részéről: 212-es busszal Svábhegyig, onnan a 21-es busszal a végállomásig.
Gyakorlatvezetők:
Magda Gábor Zsolt (magda.gabor@ttk.mta.hu, telefon: 1157-es mellék), Piszter Gábor (piszter.gabor@ttk.mta.hu, telefon: 3035-ös mellék)
Elméleti összefoglaló
Bevezetés
A gyakorlat célja hozzásegíteni a hallgatókat ahhoz, hogy megismerkedhessenek napjaink talán legizgalmasabb felületvizsgáló eszközcsoportjának (SPM, Scanning Probe Microscope) egyikével, az STM-mel (Scanning Tunneling Microscope, pásztázó alagútmikroszkóp), mérések végzésével és a nyert képek számítógépes kiértékelésével. Az STM elektromosan vezető felületek atomi léptékű vizsgálatára és módosítására alkalmas eszköz. Az alagútmikroszkópban egy igen hegyes tűt mozgatunk a felülettől nanométeres távolságra, miközben a tű és a minta közé volt nagyságrendű feszültséget kapcsolunk. Az STM leggyakrabban alkalmazott üzemmódjában (állandó áramú leképezés) miközben a minta síkjában a tűvel pásztázó mozgást végzünk, egy visszacsatoló hurokkal a tű felület fölötti magasságát úgy szabályozzuk, hogy a tű és a minta közötti, általában nanoamper nagyságrendű alagútáram állandó értéken maradjon. A tű így kialakuló háromdimenziós mozgása adja az STM képet. A megfelelő módon zajvédett (elektromos és mechanikai zajok szempontjából egyaránt) STM elegendően sima felületeken - pl. hasított egykristály - rutinszerűen képes elérni az atomi felbontást, lásd az 1.1 ábrán.
Az alagúteffektus
Ha két vezető anyag közé elektromos feszültséget kapcsolunk, és ezeket összeérintjük, áram folyik. Az elektródákat eltávolítva egymástól az áram megszűnik. Az áram megszűnése azonban nem ugrásszerűen, hanem fokozatosan történik, az elektródákat távolítva az áram exponenciálisan csökken. Makroszkópikus elektróda távolságoknál az áram mérhetetlenül kicsivé válik, tehát minden gyakorlati szempontból nullának tekinthető. Viszont ha az elektródák távolsága elegendően kicsi, azaz a nanométer (nm) tartományba esik, akkor jól mérhető áram fog folyni. Ezt a jelenséget kvantummechanikai alagúteffektusnak nevezzük.
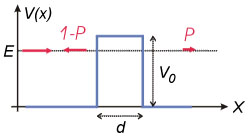
Az alagúteffektus elmélete szerint egy részecske egy  szélességű és
szélességű és 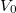 magasságú potenciálgáton (1.2. ábra) akkor is véges valószínűséggel képes áthatolni, ha az
magasságú potenciálgáton (1.2. ábra) akkor is véges valószínűséggel képes áthatolni, ha az  energiája kisebb a potenciálgát magasságánál,
energiája kisebb a potenciálgát magasságánál, 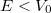 . Az áthaladás valószínűsége:
. Az áthaladás valószínűsége:
![\[ P = \frac{16E\left( V_0 - E\right)}{V_0^2}\cdot e^{-2\kappa d} \]](/images/math/8/5/9/8593addce489e1eb2e03882003c42f22.png)
ahol 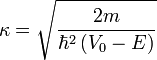 (Ez a képlet csak aszimptotikusan,
(Ez a képlet csak aszimptotikusan,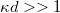 határesetben igaz.)
határesetben igaz.)
Fém elektródák esetén a potenciálgát 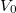 magassága elektronvolt (
magassága elektronvolt (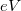 ) nagyságrendű. Ilyenkor az (1) képlet szerint az átmeneti valószínűség kb. tizedére csökken, ha az elektródák távolságát
) nagyságrendű. Ilyenkor az (1) képlet szerint az átmeneti valószínűség kb. tizedére csökken, ha az elektródák távolságát 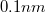 -rel növeljük. Az STM-ben szokásos
-rel növeljük. Az STM-ben szokásos 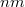 nagyságrendű
nagyságrendű  értékek esetén
értékek esetén  jellegzetes értéke kb.
jellegzetes értéke kb. 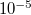 .
.
Az alagútáram
Ha a két elektróda közé 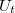 előfeszítést kapcsolunk, akkor az
előfeszítést kapcsolunk, akkor az 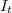 alagútáram nagysága ettől a feszültségértéktől, az elektródák anyagától és az elektródák közti távolságtól fog függeni. Az alagútáram az alábbi módon becsülhető meg.
alagútáram nagysága ettől a feszültségértéktől, az elektródák anyagától és az elektródák közti távolságtól fog függeni. Az alagútáram az alábbi módon becsülhető meg.
A fémes vezetés legegyszerűbb modellje, a szabadelektron gáz modell szerint a vezetési elektronok a fém belsejében szabadon mozoghatnak, de a határfelületnek belülről nekiütközve visszaverődnek a fém belsejébe. Mivel a fémek tipikus elektronsűrűsége 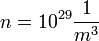 körüli és az elektronok átlagos sebessége
körüli és az elektronok átlagos sebessége 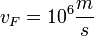 , időegységenként kb.
, időegységenként kb. 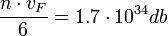 elektron ütközik a határfelület egységnyi felületén. Ha az (1) képletet figyelembe véve feltesszük, hogy ezeknek
elektron ütközik a határfelület egységnyi felületén. Ha az (1) képletet figyelembe véve feltesszük, hogy ezeknek  -ed része jut át a másik elektródába, nulladik közelítésként az alagútáramra
-ed része jut át a másik elektródába, nulladik közelítésként az alagútáramra 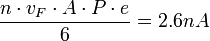 adódik, ahol
adódik, ahol  az elektron töltése, továbbá föltételeztük, hogy az áram egy
az elektron töltése, továbbá föltételeztük, hogy az áram egy 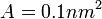 területű alagút csatornán át folyik. (Ez utóbbi érték megfelel egy egyatomos STM tű csúcs felületének.) Bár a kapott alagútáram nagyságrendileg valóban az STM esetén szokásos
területű alagút csatornán át folyik. (Ez utóbbi érték megfelel egy egyatomos STM tű csúcs felületének.) Bár a kapott alagútáram nagyságrendileg valóban az STM esetén szokásos 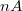 tartományba esik, ez a durva becslés több szempontból is pontosításra szorul. Elsősorban figyelembe kell venni a Pauli elvet, ugyanis egy adott
tartományba esik, ez a durva becslés több szempontból is pontosításra szorul. Elsősorban figyelembe kell venni a Pauli elvet, ugyanis egy adott  energiájú elektron csak akkor juthat át a másik elektródába, ha azon az energián rendelkezésre áll ott nem betöltött energiaállapot. Másodsorban az is lényeges módon befolyásolja az alagútáramot, hogy milyen az elektronok energia szerinti eloszlása az elektródákban. Ezen hatások figyelembevétele a következő módon lehetséges.
energiájú elektron csak akkor juthat át a másik elektródába, ha azon az energián rendelkezésre áll ott nem betöltött energiaállapot. Másodsorban az is lényeges módon befolyásolja az alagútáramot, hogy milyen az elektronok energia szerinti eloszlása az elektródákban. Ezen hatások figyelembevétele a következő módon lehetséges.
![\left[ \frac{-L}{2},\frac{L}{2} \right]](/images/math/5/8/d/58d9dd56c26f5c3724cfd82bde14cb36.png) intervallumban elhelyezkedő fémben az elektron
intervallumban elhelyezkedő fémben az elektron 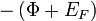 potenciált, az intervallumon kívüli vákuumban nulla potenciált érzékel. A
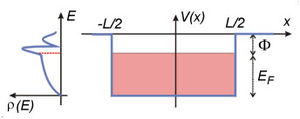
potenciált, az intervallumon kívüli vákuumban nulla potenciált érzékel. A ![\left[-\left( \Phi+E_F \right),-\Phi \right]](/images/math/c/8/e/c8e946ef670885e121b5fd0ddbcad97c.png) közötti energiaszintek betöltöttek, az e fölötti szintek üresek. A bal oldali ábra egy hipotetikus állapotsűrűség függvényt mutat. A piros szaggatott vonal jelöli a Fermi szint helyét.
közötti energiaszintek betöltöttek, az e fölötti szintek üresek. A bal oldali ábra egy hipotetikus állapotsűrűség függvényt mutat. A piros szaggatott vonal jelöli a Fermi szint helyét.A fémek legegyszerűbb kvantumfizikai modellje, a potenciálkád modell (1.3. ábra) feltételezi, hogy a vezetési elektronok egy potenciál dobozba vannak zárva. Ebben a modellben a fém vezetési elektronjainak (azaz a fémben szabad mozgásra képes, ún. delokalizált, tehát nem valamely atomhoz kötött elektronoknak) két leglényegesebb tulajdonságát vesszük figyelembe:
- a) az elektronok a fémben kötöttek, kiszabadításukhoz munkát kell befektetni, ennek a legkisebb nagysága a
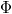 kilépési munka
kilépési munka
- b) az elektronok egy véges energiasávot foglalnak el, melynek szélessége az
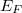 Fermi energia és a legmagasabb energiájú betöltött állapot energiája a Fermi szint.
Fermi energia és a legmagasabb energiájú betöltött állapot energiája a Fermi szint.
Ennek az energiasávnak a szerkezetét a 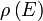 állapotsűrűség függvény (Density of States, DOS) írja le, definíció szerint
állapotsűrűség függvény (Density of States, DOS) írja le, definíció szerint 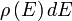 az
az  energia körüli
energia körüli 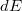 infinitezimális energiaintervallumban található elektronállapotok száma. Az állapotsűrűség függvény ismeretében az adott szilárdtest legtöbb fontos adata (pl. elektromos, optikai, mechanikai, termodinamikai jellemzők) kiszámítható, és mint alább megmutatjuk, az alagútáram nagyságát is a DOS határozza meg.
infinitezimális energiaintervallumban található elektronállapotok száma. Az állapotsűrűség függvény ismeretében az adott szilárdtest legtöbb fontos adata (pl. elektromos, optikai, mechanikai, termodinamikai jellemzők) kiszámítható, és mint alább megmutatjuk, az alagútáram nagyságát is a DOS határozza meg.
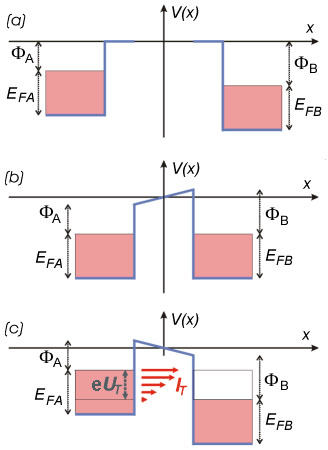
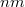 közelségbe hozzuk, a Fermi szintek kiegyenlítődnek és kialakul a kontaktpotenciál.* (c) Az elektródák közé
közelségbe hozzuk, a Fermi szintek kiegyenlítődnek és kialakul a kontaktpotenciál.* (c) Az elektródák közé 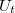 előfeszítést kapcsolunk. Az
előfeszítést kapcsolunk. Az 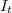 alagútáram az
alagútáram az 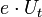 szélességű energiaintervallumban folyik, az A elektróda betőltőtt állapotaiból a B elektróda üres állapotaiba. A nagyobb energiájú komponensek áram járuléka nagyobb, a nagyobb átmeneti valószínűségük miatt.
szélességű energiaintervallumban folyik, az A elektróda betőltőtt állapotaiból a B elektróda üres állapotaiba. A nagyobb energiájú komponensek áram járuléka nagyobb, a nagyobb átmeneti valószínűségük miatt.A 1.4/a. ábrán a két, egymástól kezdetben makroszkópikus távolságban lévő elektróda potenciálkád sávszerkezetét ábrázoltuk. Általános esetben a két elektróda (A és B) különböző anyagú, ezért Fermi energiájuk és kilépési munkájuk is eltérő, az ábrán az A elektróda Fermi szintje magasabban helyezkedik el a B Fermi szintjénél. Ha az elektródákat olyan közelségbe hozzuk egymáshoz, hogy az elektronok számottevő valószínűséggel közlekedhessenek egyikből a másikba (alagúteffektus által), akkor az A elektródából elektronok kezdenek átfolyni a B elektródába. Ez azt jelenti, hogy A pozitív, B pedig negatív töltést nyer, minek hatására mindkét elektróda a vákuumszinthez képest elektrosztatikus potenciális energiára tesz szert. Mivel ahhoz, hogy a végtelenből a "+" töltésű A felületéig vigyünk egy elektront "-" munkát, ahhoz viszont, hogy a "-" töltésű B felületéig vigyünk egy elektront "+" munkát kell végezni, A energiaszintjei "-", B energiaszintjei pedig "+" irányban tolódnak el a vákuumszinthez képest. Következésképpen a két elektróda közt létrejön az ún. kontaktpotenciál. A töltésátfolyás mindaddig tart, amíg a két elektróda Fermi szintje ki nem egyenlítődik (1.4/b. ábra). Mint arról egyszerű számolással meggyőződhetünk, a kiegyenlítődés eléréséhez (fémek esetében) a vezetési elektronok összes számához képest elegendő igen kevés elektronnak átjutnia A-ból B-be, tehát a sávszélességek változása teljesen elhanyagolható.
Ha ezután a két,  távolságban lévő elektróda közé
távolságban lévő elektróda közé 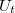 előfeszítést kapcsolunk, a 1.4/c. ábrán vázolt helyzet áll elő. Ilyenkor csak az ábrán jelölt,
előfeszítést kapcsolunk, a 1.4/c. ábrán vázolt helyzet áll elő. Ilyenkor csak az ábrán jelölt, 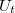 szélességű energiasávba eső elektronok juthatnak át az A elektródából a B elektródába, mert csak ezeken az energiákon vannak az A elektródában betöltött, a B elektródában pedig üres állapotok. Mivel adott
szélességű energiasávba eső elektronok juthatnak át az A elektródából a B elektródába, mert csak ezeken az energiákon vannak az A elektródában betöltött, a B elektródában pedig üres állapotok. Mivel adott  energia körüli
energia körüli 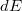 intervallumban átjutó elektronok száma a
intervallumban átjutó elektronok száma a  átmeneti valószínűségtől, valamint attól függ, hogy a két elektródában hány állapot van ebben a
átmeneti valószínűségtől, valamint attól függ, hogy a két elektródában hány állapot van ebben a 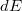 intervallumban, a teljes
intervallumban, a teljes 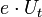 energiaintervallumban folyó
energiaintervallumban folyó 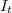 alagútáram:
alagútáram:
![\[ I_t \propto \int_{E_F}^{E_F+eU_t} \rho_{tu} \left( E-eU_t \right) \cdot \rho_{minta} \left( E \right) \cdot P \left( E,U_t \right)\,\mathrm{d}E \]](/images/math/9/2/a/92a58663b9c9f5f1a2042fd197198705.png)
Ha feltesszük, hogy a  és a tű DOS értékek csak elhanyagolható módon függenek az energiától, a következő összefüggést kapjuk:
és a tű DOS értékek csak elhanyagolható módon függenek az energiától, a következő összefüggést kapjuk:
![\[ I_t \propto \int_{E_F}^{E_F+eU_t} \rho_{minta}\left( E \right) \,\mathrm{d}E \]](/images/math/6/8/3/6837ead8492dcd174981a9bbf048b595.png)

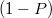 valószínűséggel verődik vissza.
valószínűséggel verődik vissza.