Piroelektromos anyagok
Szerkesztés alatt!
A mérés célja:
- Megismertetni a hallgatókat a piroelektromos illetve ferroelektromos anyagok legfontosabb tulajdonságaival, ezek mérési módszereivel és a piroelektromos effektus gyakorlati alkalmazásával a piroelektromos detektor példáján.
Ennek érdekében:
- összefoglaljuk a ferroelektromos anyagokra vonatkozó legfontosabb ismereteket,
- felvesszük egy ferroelektromos anyag hiszterézisgörbéjének, a remanens polarizációnak és a koercitív térnek a hőmérsékletfüggését, és meghatározzuk az anyag Curie-hőmérsékletét,
- meghatározzuk az anyag piroelektromos együtthatójának hőmérsékletfüggését,
- megvizsgálunk egy infravörös sugárzás érzékelésére alkalmas piroelektromos detektort.
Tartalomjegyzék[elrejtés] |
Elméleti összefoglaló
Dielektrikumok
A dielektrikumok egyik jellegzetes tulajdonsága, hogy elektromos tér hatására polarizálódnak, ami a bennük a tér által létrehozott , illetve a tér nélkül is meglévő dipólusok rendeződésének következménye. A dipólusok orientációjának mértékét – az anyag polarizálódását - jellemezhetjük a 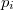 molekuláris dipólusmomentum vektorok összegével, vagyis az anyag teljes dipólusmomentumával (
molekuláris dipólusmomentum vektorok összegével, vagyis az anyag teljes dipólusmomentumával (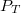 ):
):
![\[ P_T = \sum p_i \]](/images/math/f/9/c/f9cc81440d10108934ade27ac2783869.png)
ahol az i index az egyes molekuláris dipólusokat jelöli. Ez a mennyiség azonban lokális jellemzésre nem alkalmas, ezért a polarizációt inkább a térfogategység dipólusmomentumával szokás jellemezni:
![\[ P = \dfrac{dP_T}{dV} \]](/images/math/6/a/2/6a2e6babd3d58e876fcbbd46c358f758.png)
ahol 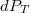 a
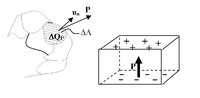
a 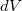 térfogat teljes dipólusmomentuma. Az így definiált vektormennyiség az elektromos polarizáció, vagy polarizáció vektor. A polarizáció egyik következménye az, hogy az anyag belsejében létrejött dipólusok saját elektromos tere is megjelenik, így ott az elektromos térerősség a külső elektromos tér és a dipólusok lokális terének eredője lesz. Egy másik fontos következménye az, hogy a po polarizált anyag határfelületén elektromos töltések jelennek meg. Mint kimutatható, egy
térfogat teljes dipólusmomentuma. Az így definiált vektormennyiség az elektromos polarizáció, vagy polarizáció vektor. A polarizáció egyik következménye az, hogy az anyag belsejében létrejött dipólusok saját elektromos tere is megjelenik, így ott az elektromos térerősség a külső elektromos tér és a dipólusok lokális terének eredője lesz. Egy másik fontos következménye az, hogy a po polarizált anyag határfelületén elektromos töltések jelennek meg. Mint kimutatható, egy 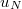 normálisú,
normálisú, 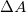 nagyságú felületelemen (1a.ábra) ahol a polarizáció
nagyságú felületelemen (1a.ábra) ahol a polarizáció  , a polarizációs töltés nagyságát (
, a polarizációs töltés nagyságát (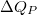 ) az alábbi összefüggés adja meg:
) az alábbi összefüggés adja meg:
![\[ \Delta Q_P = \Delta A u_N P \]](/images/math/a/d/0/ad09737bd8be434c8fa3b5c90d92dd37.png)
Ennek megfelelően, egy derékszögű hasáb alakú mintán, amelyben a polarizáció vektor homogén, és merőleges az egyik szemben lévő lap-párra (1b.ábra), az ezen a két lapon megjelenő polarizációs töltések nagysága (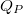 ) :
) :
![\[ Q_P = A P \]](/images/math/7/3/6/7363c85c9255f74d38aa09ed97c01316.png)
Piroelektromos anyagok, piroelektromos effektus
Az anyagban elektromos polarizációt (illetve polarizáció-változást) többféle hatás okozhat. (részletesebben l. a „Piezoelektromos állandók mérése” c. laboratóriumi segédletben), vannak azonban olyan anyagok, amelyekben külső hatás nélkül is kialakulhat nullától különböző polarizáció. Az így létrejött polarizációt "spontán polarizációnak" (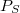 ), a spontán polarizációval rendelkező anyagokat pedig "piroelektromos anyagok"nak nevezik. Anélkül, hogy a részletekbe belemennénk, megjegyezzük, hogy a spontán polarizáció kialakulásának energetikai okai vannak: az anyag ilyen módon kedvezőbb energetikai állapotba kerül a polarizálatlanhoz képest. Kristályokban spontán polarizáció csak a kristályszerkezet által maghatározott irányban (vagy irányokban) jöhet létre, az ilyen irányt (irányokat) a kristály poláris tengelyének (tengelyeinek) nevezik.
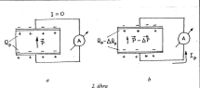
A piroelektromos anyag spontán polarizációját elvileg a felületén elhelyezkedő polarizációs töltések mérése útján a (3) illetve (4) egyenlet alapján határozhatjuk meg. A töltések például úgy lennének mérhetők, hogy a két ellenkező előjelű töltést tartalmazó felületen elektródokat helyezünk el, és mérjük az összekötésük után folyó áramot. Ez a közvetlen módszer azonban nem alkalmazható, mert a polarizált dielektrikum felületén a polarizációs töltések általában közvetlenül nem figyelhetők meg. Ennek oka az, hogy az anyag belsejéből, vagy a környező közegből (pl. levegő) kompenzáló töltések áramlanak a felületekre, és igen rövid idő alatt semlegesítik a polarizációs töltéseket (2a.ábra).
), a spontán polarizációval rendelkező anyagokat pedig "piroelektromos anyagok"nak nevezik. Anélkül, hogy a részletekbe belemennénk, megjegyezzük, hogy a spontán polarizáció kialakulásának energetikai okai vannak: az anyag ilyen módon kedvezőbb energetikai állapotba kerül a polarizálatlanhoz képest. Kristályokban spontán polarizáció csak a kristályszerkezet által maghatározott irányban (vagy irányokban) jöhet létre, az ilyen irányt (irányokat) a kristály poláris tengelyének (tengelyeinek) nevezik.
A piroelektromos anyag spontán polarizációját elvileg a felületén elhelyezkedő polarizációs töltések mérése útján a (3) illetve (4) egyenlet alapján határozhatjuk meg. A töltések például úgy lennének mérhetők, hogy a két ellenkező előjelű töltést tartalmazó felületen elektródokat helyezünk el, és mérjük az összekötésük után folyó áramot. Ez a közvetlen módszer azonban nem alkalmazható, mert a polarizált dielektrikum felületén a polarizációs töltések általában közvetlenül nem figyelhetők meg. Ennek oka az, hogy az anyag belsejéből, vagy a környező közegből (pl. levegő) kompenzáló töltések áramlanak a felületekre, és igen rövid idő alatt semlegesítik a polarizációs töltéseket (2a.ábra).
A polarizáció változása azonban meghatározható, hiszen ez a felületi töltések mennyiségének változásával jár, ami a 2b.ábrán látható módon a külső áramkörben áramot létesít, még mielőtt egyéb töltéskiegyenlítő effektusok számottevő hatást fejthetnének ki. Az ilyenkor folyó polarizációs áram (4) alapján:
![\[ I_P = \dfrac{\Delta Q_P}{\Delta t} =A \dfrac{\Delta P}{\Delta t} \]](/images/math/4/e/6/4e66f66811ccf97fa391c7fba300c0da.png)
Eszerint az áram mérésével a polarizáció változásának sebessége (5) alapján meghatározható.
A piroelektromos anyagok a nevüket arról a jellegzetes tulajdonságukról kapták, hogy spontán polarizációjuk függ a hőmérséklettől, és ezért hőmérsékletváltozás hatására felületükön elektromos töltés jelenik meg. Ez a jelenség a "piroelektromos effektus". A hőmérsékletváltozás (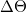 ) által (állandó mechanikai feszültség és állandó külső elektromos tér esetén) okozott spontán polarizáció-járulék i-edik komponense a
) által (állandó mechanikai feszültség és állandó külső elektromos tér esetén) okozott spontán polarizáció-járulék i-edik komponense a
![\[ P_{Si} = \gamma_i \Delta \Theta \]](/images/math/2/b/e/2bee0394c051e813e7f18899e7572239.png)
egyenlettel adható meg (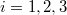 ), ahol
), ahol 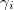 a piroelektromos állandó-vektor i-edik komponense. Mivel a mérés során egyetlen polarizációs iránnyal rendelkező anyagot vizsgálunk, a (6) egyenletet index nélküli alakban is használhatjuk az alábbiak szerint: 3 iránynak – a szokásoknak megfelelően – a spontán polarizáció irányát választjuk, így
a piroelektromos állandó-vektor i-edik komponense. Mivel a mérés során egyetlen polarizációs iránnyal rendelkező anyagot vizsgálunk, a (6) egyenletet index nélküli alakban is használhatjuk az alábbiak szerint: 3 iránynak – a szokásoknak megfelelően – a spontán polarizáció irányát választjuk, így 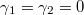 , ezért bevezetve a
, ezért bevezetve a 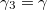 , és a
, és a 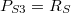 jelölést, a piroelektromos effektus által okozott polarizáció-járulékra a
jelölést, a piroelektromos effektus által okozott polarizáció-járulékra a
![\[ P_{S} = \gamma \Delta \Theta \]](/images/math/4/5/5/455c1d924e9d89c4de28888cb14e9b61.png)
összefüggést kapjuk. A piroelektromos effektus kísérletileg úgy vizsgálható, hogy a piroelektromos anyagból megfelelő módon kivágott mintát a 2. ábrán látható áramkörbe kapcsoljuk, és változtatjuk a hőmérsékletét. Ekkor a (7) egyenletnek megfelelően változik a minta polarizációja, ami a külső körben (5) alapján az
![\[ I_{P} = \gamma \cdot A \dfrac{\Delta \Theta}{\Delta t} \]](/images/math/7/8/3/7830705eab06a76fb6dc7677ac841497.png)
polarizációs áramot okoz. (Ezt az áramot - eredetére utalva – gyakran piroáramnak nevezik.) Ha tehát ismerjük a minta hőmérsékletének időbeli változását, akkor a piroáram mérésével (8)-ból a piroelektromos együttható meghatározható.
Az egyik legismertebb piroelektromos kristály a triglicinszulfát(TGS), de gyakran használt piroelektromos anyag a bárium titanát (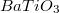 ) és a lítium niobát (
) és a lítium niobát (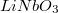 ) is. Ezenkívül használnak piroelektromos kerámiákat (ezek porrátört piroelektromos kristályból préseléssel és kiégetéssel készült anyagok) -ilyen anyagot fogunk a mérés során vizsgálni- és léteznek piroelektromos polimer fóliák (PVDF, polivinil-difluorid) is.
) is. Ezenkívül használnak piroelektromos kerámiákat (ezek porrátört piroelektromos kristályból préseléssel és kiégetéssel készült anyagok) -ilyen anyagot fogunk a mérés során vizsgálni- és léteznek piroelektromos polimer fóliák (PVDF, polivinil-difluorid) is.
Ferroelektromos anyagok, ferroelektromos hiszterézis
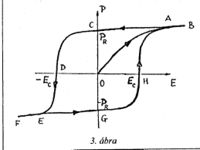
A kristályos piroelektromos anyagok egy részében a spontán polarizáció iránya külső elektromos térrel megváltoztatható. Ha a polarizációnak csak egy lehetséges iránya van, akkor ez azt jelenti, hogy a polarizáció vektor ellenkező irányúvá tehető, több polarizációs irány esetén pedig a lehetséges irányok bármelyikébe beforgatható. Az ilyen – változtatható irányú spontán polarizációval rendelkező – piroelektromos anyagokat "ferroelektromos anyagok"nak nevezik. Ha egy ferroelektromos anyagból készült makroszkopikus minta polarizációját megvizsgáljuk, akkor azt találjuk, hogy abban a spontán polarizáció iránya rendszerint csak kisebb tartományokban – az ún. "domének"ben – azonos. Ennek az az oka, hogy azonos irányú spontán polarizáció túlságosan nagy elektrosztatikus energiát eredményezne, ezért különböző irányba polarizált domének jönnek létre, és ezek - az elektrosztatikus energia csökkentése érdekében - úgy rendeződnek, hogy a minta eredő polarizációja kicsi (rendszerint nullához közeli értékű) legyen. Ennek a következménye például az, hogy egy ilyen – rendezetlen doméneket tartalmazó – ferroelektromos anyag a kis eredő polarizáció miatt csak igen gyenge piroelektromos effektust mutat. Megfelelő erősségű elektromos térrel azonban a ferroelektromos anyagban a domének polarizációja egy irányba rendezhető, és ez az állapot – annak ellenére, hogy energetikailag nem kedvező – hosszú időn át fennmaradhat. Az így kapott polarizált ferroelektromos anyag már rendszerint jelentős piroelektromos effektust mutat. A domének elektromos térrel történő rendezése során a minta polarizációja sajátos, a ferroelektromos anyagokra jellemző módon változik: a polarizációnak az elektromos terétől való függését egy jellegzetes zárt hurok, az ú.n. "ferroelektromos hiszterézis görbe" (vagy "hiszterézis hurok") adja meg. Egy ilyen jellegzetes hiszterézis hurok látható a 3. ábrán.
Az eredetileg polarizálatlan mintát ("O" pont) elektromos térbe helyezve, a domének a térerősség növelésével fokozatosan a tér irányába polarizálódnak át ( a szokásos kifejezéssel: a tér irányába „fordulnak”), így az eredő polarizáció növekszik ("OA" szakasz). Amikor már az összes domén a tér irányába fordult, a polarizáció nem nő tovább ("AB" szakasz). Ha ebben az ú.n. "telítési állapot"ban a térerősséget csökkentjük, akkor a domének rendezett állapota lényegében megmarad, ezért a polarizáció csak kis mértékben csökken ("BC" szakasz), és nulla térerősségnél ("C" pont) is jelentős, ú.n. "maradék" ("remanens") "polarizáció"t (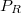 ) találunk. Ez a ferroelektromos anyag fontos jellemzője. Ellenkező irányú térrel a polarizáció nullára csökkenthető ("CD" szakasz), az ehhez szükséges elektromos térerősség az anyag egy másik jellemzője, amelyet "koercitív tér"nek (
) találunk. Ez a ferroelektromos anyag fontos jellemzője. Ellenkező irányú térrel a polarizáció nullára csökkenthető ("CD" szakasz), az ehhez szükséges elektromos térerősség az anyag egy másik jellemzője, amelyet "koercitív tér"nek (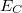 ) neveznek. Az ellenkező irányú tér növelésével ellenkező irányú telítési polarizáció ("DEF" szakasz), majd
) neveznek. Az ellenkező irányú tér növelésével ellenkező irányú telítési polarizáció ("DEF" szakasz), majd 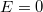 -nál ("G" pont) ellenkező irányú remanens polarizáció jelenik meg. A tér eredeti irányban való növelése a polarizációt előbb nullára csökkenti ("GH" szakasz), majd újra telítésben viszi ("HAB" szakasz), amivel a hiszterézis hurok zárul és újabb hasonló ciklus önmagát ismétli.
A ferroelektromos állapot egyikjellegzetessége, hogy csak egy bizonyos, az anyagtól függő
-nál ("G" pont) ellenkező irányú remanens polarizáció jelenik meg. A tér eredeti irányban való növelése a polarizációt előbb nullára csökkenti ("GH" szakasz), majd újra telítésben viszi ("HAB" szakasz), amivel a hiszterézis hurok zárul és újabb hasonló ciklus önmagát ismétli.
A ferroelektromos állapot egyikjellegzetessége, hogy csak egy bizonyos, az anyagtól függő 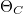 hőmérséklet, az ú.n. "Curie-hőmérséklet" (vagy "Curie-pont") alatt áll fenn. Ennek oka az, hogy túl magas hőmérsékleten a molekuláris dipólusok rendezett állapota a hőmozgás miatt nem tud kialakulni. Az anyag hőmérsékletét a Curie-pont fölé emelve, az anyag spontán polarizációja eltűnik, a hiszterézis hurok által bezárt terület nullára csökken. (egyúttal nulla lesz a remanens polarizáció és a koercitív tér), s Curie-ponton történő áthaladás során az anyag számos fizikai tulajdonsága (pl. dielektromos ál állandó, fajhő, piroelektromos állandó) drasztikus változáson megy át. Az anyagnak ezt az állapotát "paraelektromos állapot"nak nevezik. Ha az anyag hőmérsékletét a Curie-pont alá csökkentjük, akkor ismét ferroelektromossá válik. (A kristály viselkedésének a Curie-hőmérsékleten bekövetkező változása a kristály szerkezetében bekövetkező átalakulással (fázisátalakulással) függ össze.)
hőmérséklet, az ú.n. "Curie-hőmérséklet" (vagy "Curie-pont") alatt áll fenn. Ennek oka az, hogy túl magas hőmérsékleten a molekuláris dipólusok rendezett állapota a hőmozgás miatt nem tud kialakulni. Az anyag hőmérsékletét a Curie-pont fölé emelve, az anyag spontán polarizációja eltűnik, a hiszterézis hurok által bezárt terület nullára csökken. (egyúttal nulla lesz a remanens polarizáció és a koercitív tér), s Curie-ponton történő áthaladás során az anyag számos fizikai tulajdonsága (pl. dielektromos ál állandó, fajhő, piroelektromos állandó) drasztikus változáson megy át. Az anyagnak ezt az állapotát "paraelektromos állapot"nak nevezik. Ha az anyag hőmérsékletét a Curie-pont alá csökkentjük, akkor ismét ferroelektromossá válik. (A kristály viselkedésének a Curie-hőmérsékleten bekövetkező változása a kristály szerkezetében bekövetkező átalakulással (fázisátalakulással) függ össze.)
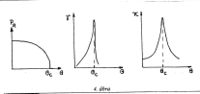
A 4.ábrán a ferroelektromos anyagok polarizációjának (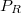 ), piroelektromos állandójának (
), piroelektromos állandójának ( ) és dielektromos állandójának (
) és dielektromos állandójának (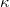 ) jellegzetes hőmérsékletfüggését mutatja be a Curie-hőmérséklet közelében.
) jellegzetes hőmérsékletfüggését mutatja be a Curie-hőmérséklet közelében.
A legismertebb ferroelektromos anyagok egyike a laboratóriumunkban vizsgálandó TGS, de ilyen kristályos anyag például a kálium-dihidrogén-foszfát (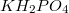 ; szokásos rövidítéssel: KDP), a bárium-titanát, a lítium-tantalát és a lítium-niobát is. Előállíthatók ferroelektromos kerámiák is, sőt egyes folyadékkristályok (rendezett láncmolekulákat tartalmazó folyadékok) is ferroelektromosak.
; szokásos rövidítéssel: KDP), a bárium-titanát, a lítium-tantalát és a lítium-niobát is. Előállíthatók ferroelektromos kerámiák is, sőt egyes folyadékkristályok (rendezett láncmolekulákat tartalmazó folyadékok) is ferroelektromosak.
Az elvégzendő vizsgálatok és a mérőberendezések
A laboratóriumban megmérjük TGS kristályok hiszterézisének, remanens polarizációjának, koercitív terének és piroelektromos állandójának hőmérsékletfüggését, majd megvizsgálunk egy piroelektromos detektort.
Ferroelektromos anyagok vizsgálata
A ferroelektromos anyagok kutatása mind tudományos, mind pedig gyakorlati szempontból igen fontos. A tudományos vizsgálatokat az indokolja, hogy különleges és érdekes anyagfajtáról van szó, gyakorlati szempontból pedig azért fontosak ezek az anyagok, mert különböző eszközökben (pl. a sugárzás és hőmérsékletmérésre használt pirodetektorokban) felhasználják őket.
A mérőkészülék
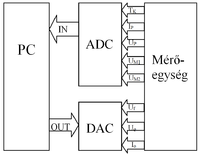
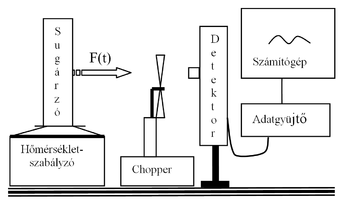
A laboratóriumban egy számítógéppel vezérelt mérőberendezéssel vizsgáljuk a ferroelektromos anyagok néhány jellegzetes tulajdonságát. A berendezés alkalmas a ferroelektromos hiszterézis (egyben a remanens polarizáció és a koercitív tér) vizsgálatára, a Curie-hőmérséklet, a piroelektromos együttható, a dielektromos állandó és az elektromos vezetőképesség mérésére. A mérés során csak a hiszterézis vizsgálatával, a Curie-hőmérséklet mérésével és a piroelektromos együttható meghatározásával foglakozunk. A számítógép egyrészt vezérli a mérési folyamatot (fűtést szabályoz, elektromos feszültséget, áramot ad a mérendő mintára), másrészt a mérőműszerekkel a mért mennyiségeket összegyűjti, tárolja és kiértékeli. A mérési összeállítás működését bemutató blokkdiagram az 5. ábrán látható.
A számítógép a mérőegységgel két jelátalakító segítségével tartja a kapcsolatot. A vezérlést egy digitál-analóg átalakító, a mért adatok begyűjtését analóg-digitál átalakító végzi. Az ábrán jelölt mennyiségek az alábbiak:
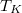 : a minta hőmérsékletével arányos jel
: a minta hőmérsékletével arányos jel
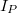 : a mintán keresztül folyó áram
: a mintán keresztül folyó áram
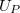 : a mintán mérhető feszültség
: a mintán mérhető feszültség
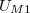 : a mintával sorbakapcsolt
: a mintával sorbakapcsolt 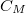 mérőkapacitás feszültsége
mérőkapacitás feszültsége
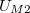 : a mintával sorbakapcsolt
: a mintával sorbakapcsolt 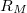 ellenállás feszültsége
ellenállás feszültsége
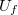 : a fűtést szabályozó feszültség
: a fűtést szabályozó feszültség
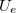 : a mintára kapcsolható nagyfeszültségű jel
: a mintára kapcsolható nagyfeszültségű jel
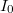 : a mintára kapcsolható áram.
: a mintára kapcsolható áram.
A mérőegység tartalmazza a méréshez szükséges elektronikai elemeket, a minta rögzítéséhez szükséges mechanikát és a fűtőrendszert, amellyel a minta hőmérséklete a kívánt módon szabályozható.
Ferroelektromos hiszterézis vizsgálata
A hiszterézisgörbe, vagyis a polarizáció ( ) – elektromos térerősség (
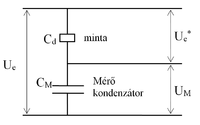
) – elektromos térerősség ( ) összefüggésének felvétele az alábbi elrendezésben történik (6.ábra). A mintát tartalmazó
) összefüggésének felvétele az alábbi elrendezésben történik (6.ábra). A mintát tartalmazó 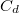 kondenzátorból és a
kondenzátorból és a 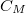 mérőkondenzátorból álló rendszerre a számítógép
mérőkondenzátorból álló rendszerre a számítógép 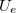 feszültséget kapcsol és (megfelelő műszerek közvetítésével) méri a mintán megjelenő
feszültséget kapcsol és (megfelelő műszerek közvetítésével) méri a mintán megjelenő 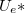 és a mérőkondenzátoron megjelenő
és a mérőkondenzátoron megjelenő 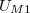 feszültséget.
Bebizonyítható, hogy
feszültséget.
Bebizonyítható, hogy 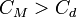 esetén
esetén 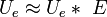 , vagyis
, vagyis 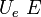 ,
másrészt a kondenzátor töltéseire érvényes, hogy
,
másrészt a kondenzátor töltéseire érvényes, hogy 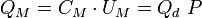 , vagyis
, vagyis 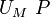 .
A mérés úgy történik, hogy a számítógéppel szabályozott
.
A mérés úgy történik, hogy a számítógéppel szabályozott 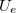 feszültség segítségével a mintán a térerősséget lineárisan változtatjuk a megfelelően választott
feszültség segítségével a mintán a térerősséget lineárisan változtatjuk a megfelelően választott 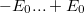 értékek között, és mérjük a polarizációval arányos
értékek között, és mérjük a polarizációval arányos 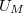 -et. A mért adatokból a számítógép meghatározza
-et. A mért adatokból a számítógép meghatározza  -t és
-t és  -t, majd ábrázolja összefüggésüket (a hiszterézisgörbét a képernyőn ábrázolja, egyúttal meghatározza a remanens polarizációt és a koercitív teret is.
-t, majd ábrázolja összefüggésüket (a hiszterézisgörbét a képernyőn ábrázolja, egyúttal meghatározza a remanens polarizációt és a koercitív teret is.
A piroelektromos együttható mérése
A piroelektromos együttható közvetett úton a hiszterézisgörbe vizsgálatával, a spontán (remanens) polarizáció hőmérsékletfüggéséből kapható meg. A mérés a  piroegyüttható
piroegyüttható 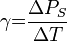 definíciós egyenleten alapul.
A másik ú.n. direkt módszernél az
definíciós egyenleten alapul.
A másik ú.n. direkt módszernél az 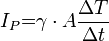 összefüggést használjuk (
összefüggést használjuk ( a hőmérséklet,
a hőmérséklet,  az idő,
az idő,  a minta felülete). Ha a mérendő mintát állandó sebességgel fűtjük, vagy hűtjük (
a minta felülete). Ha a mérendő mintát állandó sebességgel fűtjük, vagy hűtjük (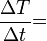 állandó), akkor
állandó), akkor 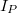 mérésével \gamma meghatározható, hiszen a két érték csak egy állandó faktorban különbözik egymástól. Ha a fűtési sebesség nem állandó, akkor a számítás kicsit bonyolultabb, de számítógép segítségével ez a feladat is megoldható (ilyenkor a
mérésével \gamma meghatározható, hiszen a két érték csak egy állandó faktorban különbözik egymástól. Ha a fűtési sebesség nem állandó, akkor a számítás kicsit bonyolultabb, de számítógép segítségével ez a feladat is megoldható (ilyenkor a 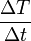 hányados pillanatnyi értékeit kell meghatározni).
hányados pillanatnyi értékeit kell meghatározni).
Mérési feladatok
Ferroelektromos hiszterézis vizsgálata
Ezeket a mérési feladatokat és méréskiértékeléseket nem kell elvégezni.
Mivel a mérőkészülék jelenleg átalakítás alatt van, a mérőprogram megismerése és a régebben elvégzett mérési adatok kiértékelését lesz a feladat.
- Nézze végig a mérőprogram funkcióit, ismerkedjen meg a mérési paraméterek beállításának lehetőségeivel és a begyűjtött adatok kiértékelésével, megjelenítésével!
- A "hiszt40", "hiszt42", "hiszt44", "hiszt45", "hiszt46", "hiszt47", "hiszt48" fájlokat beolvasva (program: hiszterézismérés, load), a hiszterézishurkokból olvassa le a spontán polarizáció és a koercitív tér értékeket! (Ezek az ábrákon relatív egységekben szerepelnek. A fájlnevekben szereplő számok a minta hőmérsékletét jelentik, oC-ban.)
- A leolvasott adatokra illesszen legalább harmadfokú polinomot. Ábrázolja a spontán polarizációt és a koercitív teret a hőmérséklet függvényében! A polinom deriválásával állítsa elő a
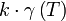 függvényt (
függvényt ( csupán egy arányossági tényező)!
csupán egy arányossági tényező)!
- Olvassa be a "gamma" nevű fájlt (program: gamma, load)! A gamma függvény TC hőmérséklet alatti szakaszáról olvasson le 5 értéket! A pontokra illesszen egy polinomot, melynek fokszáma megegyezik az előző pontban előállított
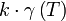 fokszámával!
fokszámával!
Vizsgálja meg az előző két pontban kapott függvények hasonlóságát!
A piroelektromos együttható direkt mérése
A mérés során egy piroelektromos lapka hőmérsékletét időben lineárisan növeljük és mérjük a keletkezett áramot. A fűtési sebességből és a minta felületének nagyságából a piroelektromos együttható, 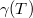 meghatározható.
A mintát egy teflonból készült mintatartóban
meghatározható.
A mintát egy teflonból készült mintatartóban 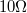 -os 10W-os ellenállással melegítjük. A minta hőmérsékletét egy Pt100,
-os 10W-os ellenállással melegítjük. A minta hőmérsékletét egy Pt100, 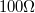 -os platina ellenállás-hőmérővel mérjük. A keletkezett piroáramot, amely
-os platina ellenállás-hőmérővel mérjük. A keletkezett piroáramot, amely 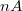 nagyságrendű egy áram-feszültség konverter (I/U konverter)
nagyságrendű egy áram-feszültség konverter (I/U konverter) 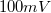 nagyságrendbe erősíti. A konverter erősítése:
nagyságrendbe erősíti. A konverter erősítése: 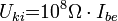 . Ezt a feszültséget mérjük és jelenítjük meg a "Logger Lite 1.4" programmal. A hőmérséklet-szabályzó az ellenállás-hőmérő értékéből és a program állásából képzett hibajellel vezérli a tápegységet, ami ennek megfelelően fűti a
. Ezt a feszültséget mérjük és jelenítjük meg a "Logger Lite 1.4" programmal. A hőmérséklet-szabályzó az ellenállás-hőmérő értékéből és a program állásából képzett hibajellel vezérli a tápegységet, ami ennek megfelelően fűti a 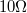 -os ellenállást. A szabályzó
-os ellenállást. A szabályzó  ,
,  ,
,  paraméterei be vannak állítva, egy egy kis túllövés után stabilizálódik a fűtési sebesség.
A beállított fűtési sebesség
paraméterei be vannak állítva, egy egy kis túllövés után stabilizálódik a fűtési sebesség.
A beállított fűtési sebesség 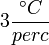 , a véghőmérséklet 100°C, a kerek minta átmérője
, a véghőmérséklet 100°C, a kerek minta átmérője 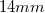 . A mintatartóból jövő vezeték árnyékolását és a vezérlő feszültség negatív pontját le kell földelni!
Az adatgyűjtőn állítsunk be 25 perc mérési időt és
. A mintatartóból jövő vezeték árnyékolását és a vezérlő feszültség negatív pontját le kell földelni!
Az adatgyűjtőn állítsunk be 25 perc mérési időt és 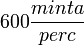 mintavételi sebességet.
mintavételi sebességet.
A PID szabályozásról az alábbi helyen olvashatnak bővebben: http://hu.wikipedia.org/wiki/PID_szab%C3%A1lyoz%C3%B3
A szabályozó működése és beállítása a gyártó műszerleírásában található:
Piroelektromos detektor vizsgálata
Elméleti összefoglaló
Az elektromágneses sugárzás detektálására szolgáló eszközök egyik csoportját a termikus detektorok alkotják. Ezeknek az eszközöknek a hőmérséklete az elnyelt sugárzás hatására megváltozik, ez pedig valamilyen fizikai tulajdonság megváltozását okozza, ami elektromos jellé alakítva mérhetővé válik.
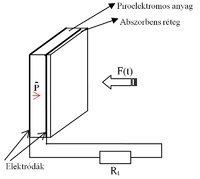
A piroelektromos anyagból a 9.ábrának megfelelő kis síkkondenzátor –szerű mintát készítenek (szokásos mérete: 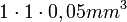 ). A detektor hőmérsékletváltozását a homloklapon elhelyezett abszorbens rétegben elnyelődő változó (periodikusan váltakozó) elektromágneses sugárzás (tipikusan
). A detektor hőmérsékletváltozását a homloklapon elhelyezett abszorbens rétegben elnyelődő változó (periodikusan váltakozó) elektromágneses sugárzás (tipikusan 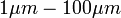 hullámhossztartományba eső közepes és távoli infravörös sugárzás) okozza. A hőmérsékletváltozás a spontán polarizáció változásán keresztül a felületi töltéssűrűség megváltozását okozza az elektródákkal ellátott, a polarizációs irányra merőleges felületeken.
A piroelektromos effektus lényegéből következik, hogy egy piroelektromos detektor csak akkor ad folyamatosan elektromos jelet, ha a hőmérséklete folyamatosan változik. Viszont állandó sugárzási teljesítmény mellett egy bizonyos hőmérsékleten a detektor termikus egyensúlyban van környezetével, vagyis nincs elektromos jele. Állandó sugárzás esetén (pl. állandó hőmérsékletű test hőmérsékleti sugárzásának, vagyis hőmérsékletének mérésekor) a detektorra jutó sugárzást meg kell szaggatni. Ez legegyszerűbben egy kis motorra szerelt szegmentált tárcsa (chopper) alkalmazásával történhet olyan módon, hogy a tárcsa lapjainak a sugárútba fordulásakor a detektorra a lapát sugárzása, a kivágott szabad rész sugárútba fordulásakor pedig a vizsgált sugárzás jut a detektorra. A két sugárzás különböző mértékben melegíti a detektort, vagyis a folyamatos hűlés-melegedés, azaz a folyamatos elektromos jel ilyen módon előáll. A lapát hőmérsékletét referenciának tekintve (ez viszonylag egyszerűen megmérhető) a kapott elektromos jel a bejövő sugárzási teljesítménnyel arányos. Az eddigiekből következik, hogy a piroelektromos detektor egy összetett hőtani és elektromos rendszert alkot.
A piroelektromos detektor jóságát (érzékenységét) alapvetően meghatározza a hőtani tervezés. A fő szempont, hogy a detektorra jutó sugárzási teljesítmény lehető legnagyobb része melegítse a detektor anyagát és minimális legyen a környezetnek átadott hő. Ezért a homlokelektródára olyan abszorbens réteget kell elhelyezni, ami jól elnyeli a detektálni kívánt elektromágneses hullámokat. A detektorlapkát úgy kell rögzíteni és az elektromos elvezetéseket kialakítani, hogy a hőelvezetések csak minimális veszteséget okozzak.
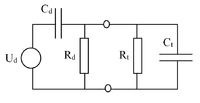
A piroelektromos detektort elektromos szempontból a 10.ábrán látható helyettesítő képpel lehet leírni.
hullámhossztartományba eső közepes és távoli infravörös sugárzás) okozza. A hőmérsékletváltozás a spontán polarizáció változásán keresztül a felületi töltéssűrűség megváltozását okozza az elektródákkal ellátott, a polarizációs irányra merőleges felületeken.
A piroelektromos effektus lényegéből következik, hogy egy piroelektromos detektor csak akkor ad folyamatosan elektromos jelet, ha a hőmérséklete folyamatosan változik. Viszont állandó sugárzási teljesítmény mellett egy bizonyos hőmérsékleten a detektor termikus egyensúlyban van környezetével, vagyis nincs elektromos jele. Állandó sugárzás esetén (pl. állandó hőmérsékletű test hőmérsékleti sugárzásának, vagyis hőmérsékletének mérésekor) a detektorra jutó sugárzást meg kell szaggatni. Ez legegyszerűbben egy kis motorra szerelt szegmentált tárcsa (chopper) alkalmazásával történhet olyan módon, hogy a tárcsa lapjainak a sugárútba fordulásakor a detektorra a lapát sugárzása, a kivágott szabad rész sugárútba fordulásakor pedig a vizsgált sugárzás jut a detektorra. A két sugárzás különböző mértékben melegíti a detektort, vagyis a folyamatos hűlés-melegedés, azaz a folyamatos elektromos jel ilyen módon előáll. A lapát hőmérsékletét referenciának tekintve (ez viszonylag egyszerűen megmérhető) a kapott elektromos jel a bejövő sugárzási teljesítménnyel arányos. Az eddigiekből következik, hogy a piroelektromos detektor egy összetett hőtani és elektromos rendszert alkot.
A piroelektromos detektor jóságát (érzékenységét) alapvetően meghatározza a hőtani tervezés. A fő szempont, hogy a detektorra jutó sugárzási teljesítmény lehető legnagyobb része melegítse a detektor anyagát és minimális legyen a környezetnek átadott hő. Ezért a homlokelektródára olyan abszorbens réteget kell elhelyezni, ami jól elnyeli a detektálni kívánt elektromágneses hullámokat. A detektorlapkát úgy kell rögzíteni és az elektromos elvezetéseket kialakítani, hogy a hőelvezetések csak minimális veszteséget okozzak.
A piroelektromos detektort elektromos szempontból a 10.ábrán látható helyettesítő képpel lehet leírni.
A terhelő ellenálláson keletkező feszültség, amit a detektor válaszjelének neveznek, a következő:
 ,
,
ahol:
 : piroelektromos együttható
: piroelektromos együttható
 : a piroelektromos anyag abszolút dielektromos állandója
: a piroelektromos anyag abszolút dielektromos állandója
 : a piroelektromos anyag sűrűsége
: a piroelektromos anyag sűrűsége
 : a piroelektromos anyag fajhője
: a piroelektromos anyag fajhője
 : a detektor felülete
: a detektor felülete
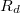 : a detektor ellenállása
: a detektor ellenállása
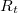 : a terhelő ellenállás
: a terhelő ellenállás 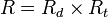
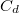 : a detektor kapacitása
: a detektor kapacitása
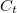 : a terhelő kapacitás
: a terhelő kapacitás 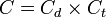
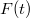 : a sugárzás teljesítményének időfüggése.
: a sugárzás teljesítményének időfüggése.
Az egyenlet különböző időtartományokra és gerjesztésekre számított megoldásai a detektor válaszjelének jellemzőire adnak felvilágosítást.
- a:
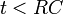 és
és 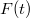 állandó, akkor
állandó, akkor
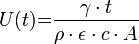
- b:
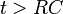 és
és 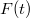 állandó, akkor
állandó, akkor
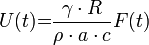
- c: ha a bejövő sugárzás teljesítménye szinuszosan változik, akkor
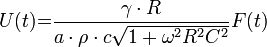 .
.
A gyakorlatban a detektorokat a válaszjel és a gerjesztés hányadosával, az érzékenységgel jellemzik:
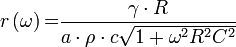
![\left[ \dfrac{V}{W}\right]](/images/math/8/8/6/88612672e845e27335258ab72d89201c.png) .
.
A fenti egyenlet alapján a tervezéshez szükséges következő megállapításokat tehetjük:
- Mivel a detektor ellenállása igen nagy (
 ) a terhelő ellenállás növelésével az érzékenység növelhető.
) a terhelő ellenállás növelésével az érzékenység növelhető.
- Ha a gerjesztés körfrekvenciája kicsi, a válaszjel független
 -tól:
-tól:
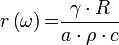
- elég nagy körfrekvencián az érzékenység fordítottan arányos
 -val:
-val:
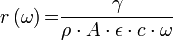
- Nagyobb érzékenység érhető el, nagy piroelektromos állandójú, kis sűrűségű, kis fajhőjű anyag felhasználásával. Alacsony körfrekvencián a dielektromos állandó értéke közömbös, magasabb tartományokban a kis
 érték kedvezőbb.
érték kedvezőbb.
- Kisfrekvenciás alkalmazásokhoz a detektort a lehető legvékonyabbra kell készíteni, nagyfrekvenciás felhasználásra a minimális felületű detektor optimális.
A piroelektromos detektor felhasználása
A fekete test sugárzására vonatkozó Planck-törvény a sugárzás intenzitásának hőmérséklet és hullámhossz szerinti eloszlását adja meg. (Erről részletesen a Hőmérsékleti sugárzás vizsgálata c. mérés anyagában olvashatnak.) A függvény menetét néhány hőmérsékletre a 11. ábra mutatja. A 0 K-nél melegebb testek által kibocsátott hőmérsékleti sugárzás intenzitásának hullámhossz szerinti eloszlása a test hőmérsékletére jellemző, az összes kisugárzott energia pedig arányos a test hőmérsékletével. A kisugárzott energia mérésével tehát a sugárzó test teljesítményére vagy hőmérsékletére lehet következtetni. Az érintésmentes hőmérsékletmérés alkalmával a test felületének emissziós tényezőjét és a test és mérőműszer közötti közeg transzmissziós tényezőjét is ismerni kell.
A piroelektromos detektor felhasználásával készített műszerek a következő területeken alkalmazhatók:
- érintés nélküli hőmérsékletmérés (optikai pirometria)
- testek felületi hőmérséklet-eloszlásának meghatározása (infravízió, infravörös kamera)
- elektromágneses sugárzás teljesítményének mérése széles (láthatótól a mikrohullámokig) tartományban
- infravörös mozgásérzékelés (vagyonvédelem).
Mérési összeállítás
A piroelektromos detektor vizsgálatára a 12.ábrán látható mérési összeállítást alkalmazzuk. A sugárforrás egy elektromosan melegített (legfeljebb 100 °C-ig) és szabályozott, 0.98 emissziós tényezőjű felület. Ennek sugárzását egy egyenáramú motorra szerelt propeller (chopper) periodikus jellé alakítja. A motor fordulatszáma a meghajtó feszültséggel változtatható. Az árnyékoló csőben levő detektor felerősített jelét digitalizálás után a számítógép monitorán ábrázoljuk. Az erősítőt egyenáramú tápegység táplálja.
Mérési feladatok
- A detektort érő szobahőmérsékletű sugárzás kézzel történő kitakarásával vizsgáljuk meg a tranziens viselkedést gyors és lassú változásokra is. A detektor jelét a számítógéphez csatlakoztatott feszültségmérővel mérjük. Az eszközt a "Logger Lite 1.4" program kezeli. Rögzítsük a jelalakokat figyelve a mérési idő és a mintavételi sebesség helyes beállítására. Értelmezzük a kapott jelalakokat!
- Állandó hőmérsékletű, 80 °C hőmérsékletű sugárforrás mellett a szaggatási frekvencia változtatásával (0.2 Hz-10 Hz) vegyük fel a kimenőfeszültség-frekvencia karakterisztikát. Az átviteli függvény maximuma 0,4 Hz körül van, ezért a 0,2 Hz-1 Hz intervallumban nagyon kis lépésekben haladjunk, hogy a maximum helye pontosan kiadódjon. A chopper fogazata nem teljesen egyenletes és a motor tengelye üt egy kicsit, így a jelek nem teljesen egyformák. Ezért minden frekvencián meg kell várni, hogy a chopper legalább egyszer teljesen körbeforduljon és az így kapott jelsorozat átlagával kell számolni.
Mivel egészen kis frekvenciákon a jel nem teljesen szinuszos, a jel nagyságának a csúcstól-csúcsig értéket tekintsük. A jel frekvenciáját a képernyőről leolvasott periódusidőből számítsuk ki. Ábrázoljuk az 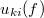 -et logaritmikus léptékben. Állapítsuk meg az átviteli függvény maximumának helyét, vagyis az optimális szaggatási frekvenciát!
-et logaritmikus léptékben. Állapítsuk meg az átviteli függvény maximumának helyét, vagyis az optimális szaggatási frekvenciát!
- Melegítsük fel a feketetestet 100°C-ra. Miután beállt a hőmérséklet, az optimális szaggatási frekvencián mérjük meg a detektor jelét. A feketetestet 5°C-os lépésekben hűtsük le szobahőmérséklet közelébe és minden hőmérsékleten, annak beállta után mérjük meg a jelet. Vizsgáljuk meg, hogy teljesül-e a Stefan-Boltzmann törvény.
Irodalom
Budó Ágoston–Mátrai Tibor: Kísérleti fizika II.
PDF formátum
A pdf formátumú leírás nem frissül tovább. Nyomtatáshoz használja az oldalsó menüsoron az Eszközök csoport Nyomtatható változat pontját.